Cassie and Amy are playing a card flash game. Cassie has a card with the fraction - 2/7 and Amy has a card with the fraction - 3/4. Write an equation to represent the product of theirs fractions then solve that equation.
( The minus is not plain -3 or -2 it’s the whole fraction)
Answers
The equation representing the product of theirs fractions is -
(- 2/7) x (- 3/4) and on solving this expression, we get 3/14.
What is a Fraction?In mathematics, fractions are represented as a numerical value, which defines a part of a whole.
Given that Cassie and Amy are playing a card flash game such that Cassie has a card with the fraction - 2/7 and Amy has a card with fraction - 3/7.
The equation that represent the product of their fractions is -
(- 2/7) x (- 3/4)
Now, solving the above expression, we get -
(- 2/7) x (- 3/4)
(1/7) x (3/2)
3/14
Therefore, the equation representing the product of theirs fractions is -
(- 2/7) x (- 3/4) and on solving this expression, we get 3/14.
To learn more about Multiplying fractions, visit the link below-
https://brainly.com/question/8743988
#SPJ1
Related Questions
If 1,200 students participated in the survey, how many rated the cafeteria food “poor”?
200 students
300 students
400 students
600 students
Answers
Answer:
The answer is 300
Answer:
300 students
Step-by-step explanation:
hope this helps!
A hardware store rents vacuum cleaners that customers may use for part or all of a day, up to 12 hours, before returning. The store charges a flat fee plus an hourly rate. Write a linear function f for the total rental cost of a vacuum cleaner.
A. f(x) = 6x + 14
B. f(x) = 3x + 14
C. f(x) = 3x + 22
D. f(x) = 6x + 24
Flat fee the store charges =
A reasonable domain for the function is: =
Cost to rent a vacuum for 7 hours =
Answers
The flat fee that the store charges is $14 and the cost for 7 hours is $56
A linear equation is on the form:
y = mx + b
where y, x are variables, m is the rate of change and b is the initial value of y.
let f for the total rental cost of a vacuum cleaner for x hours
Using the points (1, 20) and (3, 32) from the table:
\(f-f_1=\frac{f_2-f_1}{x_2-x_1} (x-x_1)\\\\f-20=\frac{32-20}{3-1} (x-1)\\\\f(x)=6x+14\)
The flat fee that the store charges is $14
The reasonable domain is 1 ≤ x ≤ 12
The cost for 7 hours is:
f(7) = 6(7) + 14 = 46
Find out more on linear equation at: https://brainly.com/question/14323743

Laura has 3.85 pounds of bananas. She goes to the store to buy 2.75 more pounds of bananas to make banana bread. Each loaf requires 0.30 pounds of bananas. How many loaves of bread can she make?
Answers
Answer:
22
Step-by-step explanation:
3.85+2.75= 6.6
6.6÷0.30= 22
Answer:
The answer is 22 loaves of bread.
Step-by-step explanation:
You add 3.85 pounds + 2.75 pounds to get the total number of pounds she bought, which is 6.6 pounds of bananas.
Then you divide your total answer of 6.6 pounds by 0.30 pounds for each loaf, to get 22 loaves of bread.
The polynomial p(x)= x3 + 7x2 – 36 has a known factor of (x + 3).
Answers

The cost of 2 footballs and 3 tennis balls is £21.73.
The cost of 5 footballs and 7 tennis balls is £53.20.
Work out the cost of
a) a football.
b) a tennis ball.
Answers
Answer: A) £7.49
B) £2.25
Step-by-step explanation:
Step 1:
Let the cost of a football be \(f\)and the cost of a tennis ball be \(t\).
Step 2:
Write the 2 equations we have from the given information:
\(2f + 3t = 21.73\) \( \textsf{(from the cost of 2 footballs and 3 tennis balls)} \)
\(5f + 7t = 53.20\) \( \textsf{(from the cost of 5 footballs and 7 tennis balls)} \)
Step 3:
Solve for one variable in one of the equations. For example, we can solve for \(f\)in the first equation:
\(2f + 3t = 21.73\)\(2f = 21.73 - 3t\)\(f = \frac{(21.73 - 3t)}{2}\)Step 4:
Substitute this expression for \(f\) into the second equation and solve for \(t\):
\(5f + 7t = 53.20\)\(5[\frac{(21.73 - 3t)}{2}] + 7t = 53.20\)\(54.325 - 7.5t + 7t = 53.20\)\(0.5t = 1.125\)\(t = 2.25\)So, the cost of a tennis ball is £2.25.
Step 5:
Substitute this value of \(t\) into the expression for \(f\) and solve for \(f\):
\(f = \frac{(21.73 - 3t)}{2}\)\(f = \frac{(21.73 - 3(2.25))}{2}\)\(f = 7.49\)So, the cost of a football is £7.49
Step 6:
Therefore, the cost of a football is £7.49 and the cost of a tennis ball is £2.25.
WVTU is a television station that has 20 thirty-second advertising slots during their regularly scheduled programming each evening. The station is now selling advertising for the first few days in November. They could sell all the slots immediately for $4,500 each, but because November 7 will be an election day, the station manager knows she may be able to sell slots at the last minute to political candidates in tight races for a price of $8,000 each. The demand for these last minute slots is estimated as follows:
8 9 10 11 12 13 14 15 16 17 18 19
Probability 0.03 0.05 0.1 0.15 0.2 0.15 0.1 0.05 0.05 0.05 0.05 0.02
Slots not sold in advance and not sold to political candidates at the last minute can be sold to local advertisers at a price of $2,000.
a. If the station manager sells all the advertising slots in advance, how much revenue will the station receive?
b. How many advertising slots should be sold in advance if the station manager wants to maximize expected revenue?
c. If the station manager sells in advance the number of slots identified in the previous question, what is the probability that the total revenue received will exceed the amount identified in part a where all slots are sold in advance?
Answers
Answer:
a. $90,000
b. 15 advertisement slots
c. 0.53
Step-by-step explanation:
Let the purchase price of the slots, c = 4,500
The salvage value of the slots, s = 2,000
The selling price of the slots, p = 8,000
a. If the store manager sells all the advertising slots in advance, the revenue received, 'R', is given as follows;
R = The number of slots, n × The purchase price for selling immediately, c
∴ R = 20 × $4,500 = $90,000
The revenue the station will receive by selling all the advertising slots in advance, R = $90,000
b. The Cost of Overage, \(C_o\) = Purchase price - Salvage value
∴ The Cost of Overage, \(C_o\) = 4,500 - 2,000 = 2,500
The Cost of Underage, \(C_u\) = Selling price - Purchase price
∴ The Cost of Underage, \(C_u\) = 8,000 - 4,500 = 3,500
P; 0.03, 0.05, 0.1, 0.15, 0.2, 0.15, 0.1, 0.05, 0.05, 0.05, 0.05, 0.02
With help of MS Excel, we get the following cumulative frequency
F(Q); 0.03, 0.08, 0.18, 0.33, 0.53, 0.68, 0.78, 0.83, 0.88, 0.93, 0.98, 1
The expected monetary value for the decision to sell the 8th slot at the last minute is given by the following relation;
\(C_u\) × [1 - F(Q)] - \(C_o\) × F(Q)
Where F(Q) = The cumulative frequency for the 8th stock
Therefore, we have;
3,500 × (1 - 0.03) - 2,500 × 0.03 = 3,300
For the 8th slot, the TV station is expected to make an extra $3,300
Using MS Excel, we get;
For the 9th slot, the profit over the purchase price = $3,020
Fot the 10th slot, the profit over the purchase price = $2,420
The profit over the purchase price for the 11th slot = $1,520
The profit over the purchase price for the 12th slot = $320
The profit over the purchase price for the 13th slot = $(-580)
The 14th = $(-1,180)
15th = $(-1,480)
16th = $(-1,780)
17th = $(-2,080)
18th = $(-2,380)
19th = $(-2,500)
Therefore, to maximize profit, only the 8th, 9th, 10th, 11th, and 12th, slots which are 5 slots should be sold late while 20 - 5 = 15 slots should be sold in advance
c. The probability that the total revenue will exceed the identified amount in part 'a' is the cumulative probability at the 12th slot which is given as follows;
P(D ≤ 12) = F(12) = 0.53.
The probability that the total revenue will exceed the identified amount in part 'a' is the cumulative probability at the 12th slot is 0.53.
What is the probability?Probability refers to a possibility that deals with the occurrence of random events. The probability of all the events occurring need to be 1.
Given information
The demand for these last minute slots is estimated
8 9 10 11 12 13 14 15 16 17 18 19
Probability 0.03 0.05 0.1 0.15 0.2 0.15 0.1 0.05 0.05 0.05 0.05 0.02
The purchase price of the slots = 4,500
The salvage value of the slots = 2,000
The selling price of the slots = 8,000
a. The revenue received
R = The number of slots × The purchase price of the slot
R = 20 × $4,500 = $90,000
The revenue the station will receive by selling all the advertising slots in advance, R = $90,000
b. The Cost of Overage = Purchase price - Salvage value
The Cost of Overage, = 4,500 - 2,000 = 2,500
The Cost of Underage, = Selling price - Purchase price
The Cost of Underage, = 8,000 - 4,500 = 3,500
Probability 0.03, 0.05, 0.1, 0.15, 0.2, 0.15, 0.1, 0.05, 0.05, 0.05, 0.05, 0.02
Cumulative frequency
F(Q); 0.03, 0.08, 0.18, 0.33, 0.53, 0.68, 0.78, 0.83, 0.88, 0.93, 0.98, 1
The expected monetary value for the decision to sell the 8th slot at the last minute
The Cost of Underage × [1 - F(Q)] - × F(Q)
Where F(Q) = The cumulative frequency for the 8th stock
Therefore, we get
3,500 × (1 - 0.03) - 2,500 × 0.03 = 3,300
For the 8th slot, the TV station is expected to make an extra $3,300
For the 9th slot, the profit over the purchase price = $3,020
For the 10th slot, the profit over the purchase price = $2,420
Similarly,
The profit over the purchase price for the 11th slot = $1,520
The profit over the purchase price for the 12th slot = $320
The profit over the purchase price for the 13th slot = $(-580)
The profit over the purchase price for the 14th = $(-1,180)
The profit over the purchase price for the 15th = $(-1,480)
The profit over the purchase price for the 16th = $(-1,780)
The profit over the purchase price for the 17th = $(-2,080)
The profit over the purchase price for the 18th = $(-2,380)
The profit over the purchase price for the 19th = $(-2,500)
Therefore, only the 8th, 9th, 10th, 11th, and 12th slots should be sold in advance to maximize profit.
c. The probability that the total revenue will exceed the identified amount in part 'a' is the cumulative probability at the 12th slot.
P(D ≤ 12) = F(12) = 0.53.
Learn more about probability here;
https://brainly.com/question/11234923
A rectangular room is
1.5
times as long as it is wide, and its perimeter is
35
meters. Find the dimension of the room.
The length is :
meters and the width is
meters.
Answers
The dimensions of the room are approximately 7 meters by 10.5 meters.
The length is 10.5 meters and the width is 7 meters.What are dimensions?In Mathematics, dimensions are referred to as measures of size such as length, width, and height of an object or a shape. A rectangle has length and width as its dimensions that define the area of a rectangle.
Let's start by using algebra to represent the information given in the problem. Let x be the width of the rectangular room, then the length is 1.5 times the width or 1.5x.
The perimeter of a rectangle is the sum of the lengths of all its sides, which can be expressed as:
\(\text{Perimeter} = 2(\text{length} + \text{width})\)
Substituting the values we have for length and width, we get:
\(\rightarrow35 = 2(1.5\text{x} + \text{x})\)
Simplifying the equation, we get:
\(\rightarrow35 = 2(2.5\text{x})\)
\(\rightarrow35 = 5\text{x}\)
\(\rightarrow\text{x}=\dfrac{35}{5}\)
\(\rightarrow\bold{x\thickapprox7}\)
So the width of the room is 7 meters.
To find the length, we can substitute x into the expression we have for the length:
\(\rightarrow\text{Length} = 1.5\text{x}\)
\(\rightarrow\text{Length} = 1.5(7)\)
\(\rightarrow\bold{Length=10.5}\)
So the length of the room is 10.5 meters.
To know more about dimensions, click on:
https://brainly.com/question/31677552
Graph Y+5=-2x and explain how you did it.
Pls Help! it’s due soon and i have no idea what to do
Answers
=
−
2
x
+
5
y
=
-
2
x
+
5
Use the slope-intercept form to find the slope and y-intercept.
Tap for more steps...
Slope:
−
2
-
2
y-intercept:
(
0
,
5
)
(
0
,
5
)
Any line can be graphed using two points. Select two
x
x
values, and plug them into the equation to find the corresponding
y
y
values.
Tap for more steps...
x
y
0
5
5
2
0
if the cost of 4 boxes is RS 140 how many boxes can be bought for RS 210
Answers
Answer:
200
Step-by-step explanation:
Answer:
6 boxes
Step-by-step explanation:
4boxes = 140RS
x. = RS 210
x = RS210×4/140
x= 6 boxes
There are 6 acts in a talent show.
An acrobat, a dancer, a guitarist, a singer, a violinist, and a whistler.
A talent show host randomly schedules the 6 acts.
Compute the probability of each of the following events.
Event A: The acrobat is first, the singer is second, the violinist is third, and the whistler is fourth.
Event B: The first four acts are the whistler, the acrobat, the guitarist, and the dancer, In any order.
Write your answers as fractions in simplest form.
P(A) =
P (B) =
Answers
The probability of Event A is 1/360 and the probability of Event B is 1/15.
For Event A, we can calculate the probability by considering the order in which the acts are scheduled.
There are 6 acts, so there are 6 possible choices for the first act. After the first act is scheduled, there are 5 remaining acts, so there are 5 possible choices for the second act.
Similarly, there are 4 possible choices for the third act, and 3 possible choices for the fourth act.
Finally, there are 2 possible choices for the fifth act, and only 1 choice remains for the last act.
Therefore, the total number of possible ways to schedule all 6 acts is:
6 x 5 x 4 x 3 x 2 x 1 = 720
Since we are only interested in one specific order of the first four acts, we need to count the number of ways to schedule the remaining two acts after the first four have been scheduled in the desired order.
There are 2 remaining acts, so there are 2 possible choices for the fifth act.
Only one act remains for the last slot.
Therefore, the total number of ways to schedule all 6 acts such that the acrobat is first, the singer is second, the violinist is third, and the whistler is fourth is:
1 x 1 x 1 x 1 x 2 x 1 = 2
Thus, the probability of Event A is:
P(A) = 2/720 = 1/360
For Event B, we want to count the number of ways to schedule the first four acts as the whistler, the acrobat, the guitarist, and the dancer, in any order.
There are 4 acts, so there are 4 possible choices for the first act. After the first act is scheduled, there are 3 remaining acts, so there are 3 possible choices for the second act.
Similarly, there are 2 possible choices for the third act, and only one choice remains for the fourth act.
Therefore, the total number of possible ways to schedule the first four acts is:
4 x 3 x 2 x 1 = 24
Since we do not care about the order in which the last two acts are scheduled, we can simply choose any two acts from the remaining 2. There are 2 ways to do this.
Therefore, the total number of ways to schedule all 6 acts such that the first four acts are the whistler, the acrobat, the guitarist, and the dancer, in any order is:
24 x 2 = 48
Thus, the probability of Event B is:
P(B) = 48/720 = 1/15
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
A computer’s random number generator produces random integers from 1 to 50. What is the probability that at least one of the first 4 generated numbers is in the 20s?
0.0016
0.1024
0.4096
0.5904
Answers
Answer:
0.5904
Step-by-step explanation:
For each number, there are only two possible outcomes. Either it is in the 20s, or it is not. The probability of a number being in the 20s is independent of other numbers. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
4 generated numbers:
This means that \(n = 4\)
Probability of a number in the 20s:
From 1 to 50, there are 50 numbers. Of those(from 20 to 29), there are 10 in the 20s. So \(p = \frac{10}{50} = 0.2\)
What is the probability that at least one of the first 4 generated numbers is in the 20s?
Either none is, or at least one is. The sum of the probabilities of these events is 1. So
\(P(X = 0) + P(X \geq 1) = 1\)
We want \(P(X \geq 1)\). So
\(P(X \geq 1) = 1 - P(X = 0)\)
In which
\(P(X = 0) = C_{4,0}.(0.2)^{0}.(0.8)^{4} = 0.4096\)
\(P(X \geq 1) = 1 - P(X = 0) = 1 - 0.4096 = 0.5904\)
Identify the slope and y intercept of the line 8x + 2y =6
Answers
Given:
8x + 2y = 6
Let's identify the slope and y-intercept of the equation.
To identify the slope and y-intercept, we are to the slope-intercept form of a linear equation:
y = mx + b
Where:
m represents the slope.
b represents the y-intercept.
Now, let's rewrite the given equation to the slope-intercept form.
Subtract 8x from both sides of the equation:
\(\begin{gathered} 8x-8x+2y=-8x+6 \\ \\ 2y=-8x+6 \end{gathered}\)Divide all terms by 2:
\(\begin{gathered} \frac{2y}{2}=-\frac{8x}{2}+\frac{6}{2} \\ \\ y=-4x+3 \end{gathered}\)Therefore, the equation in slope-intercept form is:
y = -4x + 3
Now, compare both equations:
y = mx + b
y = -4x + 3
Thus, we have the following:
Slope, m = -4
y-intercept, b = 3
Therefore, the slope of the line is -4 , while the y-intercept is 3 .
ANSWER:
• Slope = -4
,• y-intercept = 3
DIRECTIONS: Use this information to answer Parts A and B.
Marisol deposits $5,000 in a savings account earning 5.75% simple interest per year.
Part A
How much interest will Marisol earn for a period of 5 years?
Part B
Marisol receives 8,450 when she close her savings account if she made no changes to the account, for how many years did Marisol keep the account open?
Answers
Answer: 287.&. Multiply 365 x 10 Great, you get 3650 . . . Multiply 287 by 3650 which then equals 1049375 . . . Wow! The interest will then be a total of 60929$ with the 8450 that she recieved that should equal 3 years total keeping it open . . .
Step-by-step explanation: Hope This Helps! Pls mark Branliest!
For 2021, Gourmet Kitchen Products reported $22 million of sales and $19 million of operating costs (including depreciation). The company has $14 million of total invested capital. Its after-tax cost of capital is 9% and its federal-plus-state income tax rate was 25%. What was the firm's economic value added (EVA), that is, how much value did management add to stockholders' wealth during 2021?
Answers
The firm’s economic value added (EVA), that is, how much value did management add to stockholders’ wealth during 2018 is $0.42 million
What is Subtraction?Subtraction is the process of taking away a number from another. It is a primary arithmetic operation that is denoted by a subtraction symbol (-) and is the method of calculating the difference between two numbers.
here, we have,
Net operating profit = (22 million - 19 million)*(1 - 0.36)
= $1.92 million
EVA = net operating profit after taxes - invested capital*WACC
= 1.92 million - 15 million*0.10
= $0.42 million
Therefore, The firm’s economic value added (EVA), that is, how much value did management add to stockholders’ wealth during 2018 is $0.42 million.
To learn more on subtraction click:
brainly.com/question/2346316
#SPJ9
solve for x. round to the nearest tenth, if necessary. using trig to find a side

Answers
Answer:
Step-by-step explanation this is a tough one but i know everything the answer is 69
Which is the best estimate for (6.3x10-219.9x10-3written in scientific notation? 6x 10-4 60 x 10-5 6x107 60 x 108
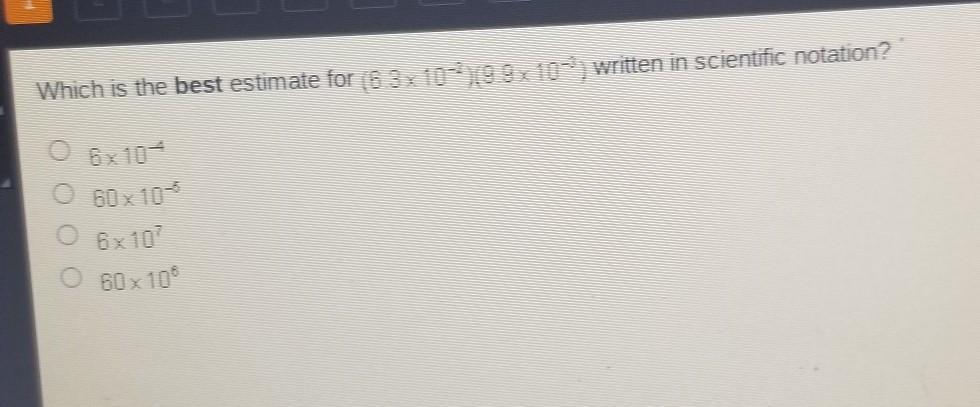
Answers
The given product is
\((6.3\times10^{-2})(9.9\times10^{-3})\)To solve this multiplication, we multiply the coefficients between each other, and the power between each other.
\((6.3\cdot9.9)(10^{-2}\cdot10^{-3})=62.37\times10^{-2-3}=62.37\times10^{-5}\)Which is approximated to
\(60\times10^{-5}\)Therefore, the right answer is B.We are looking at rectangles where one side is of length 5.0 cm. Amongst those are some that can be cut into a square and a rectangle one of which has an area of 4,0 cm². How many such rectangles are there?
A: 1
B: 2
C: 3
D: 4
E: 5
Spoiler: According to the answer key it is D but I could only find 3 variations.
Answers
the answer is D : 4
How to calculate how many of these rectangles are there?According to the problem statement, one side of the rectangle is of length 5 cm. The other side can have any length greater than 4 cm (since the area of the rectangle should be greater than 4 cm^2).
Let's call this other side "x".
We know that the area of a rectangle is given by the formula A = l*w, where l is the length and w is the width.
Therefore, we can write the equation: 5*x = A, where A is the area of the rectangle.
We can also say that the area of the square and the rectangle is equal to 4 cm^2.
If we call the side of the square "y", then we can write the equation: y^2 = 4 cm^2.
Solving for y, we get: y = 2 cm.
Therefore, the length of the rectangle that can be cut into a square and a rectangle of area 4 cm^2 is 5 cm - y = 5 cm - 2 cm = 3 cm.
So, there are 4 possible rectangles that can be cut into a square and a rectangle of area 4 cm^2: (5,3), (3,5), (6,4), and (4,6).
So the answer is D : 4
Learn more about rectangles in brainly.com/question/29123947
#SPJ1
#11 i
PROBLEM SOLVING The table shows the heights y of a competitive water-skier x seconds after jumping off a ramp.
Time (seconds), x 0 0.25 0.75 1 1.1
Height (feet), y
22 22.5 17.5 12 9.24
Write a function that models the height of the water-skier over time.
The function y =
Interpret the y-intercept.
B
22
I U
models the height.
T' T₂
When is the water-skier 5 feet above the water? Round your answer to the nearest hundredth.
70°F
Cloudy
The skier is 5 feet above the water after about
second(s).
O Search the web
J
O
L
D
(
1/10000 Word L

Answers
The function modelled for the given condition is \(y = -16x^{2} + 6x +22\) and the time after which the skier is 5 feet above the water is 1.23 seconds.
A competitive water skier's heights y, x seconds after soaring off a ramp.
For x = 0, y = 22
for x = 0.25, y = 22.5
For x = 0.75, y = 17.5
For x = 1, y = 12
For x = 1.1, y = 9.24
The general equation of a quadratic equation is y = \(ax^{2} + bx +c\)
Putting x = 0 and y = 22 in the equation, we get :
\(y = ax^{2} +bx +c\)
c = 22
Now, putting x = 1 and y =12, we get,
12 = a*1 + b*1 + 22
a +b = 12 - 22 = -10 equation (1)
Putting x = 0.25, y = 22.5,
22.5 = a* \(22.5^{2}\) +b*22.5 +22
506.25 a +22.5b = 0.5 equation(2)
Solving equation (1) and equation(2), we get :
a = -16 and b = 6 and c = 22
So, the quadratic equation becomes,
\(y = -16x^{2} + 6x +22\)
Now, Time when the skier is 5 feet above the water,
\(x = \frac{3 +\sqrt{281} }{16} = 1.23 seconds\)
Hence, the function modelled for the given condition is \(y = -16x^{2} + 6x +22\) and the time after which the skier is 5 feet above the water is 1.23 seconds.
To read more about functions, visit https://brainly.com/question/21145944
#SPJ1
Simplify the expression 10 + 2(n + 5) + 4n
Answers
Answer:
6n + 20
Step-by-step explanation:
10 + 2n + 10 +4n
6n +20
Answer:
\(10 + 2n + 10 + 4n \\ 6n + 20 \\ 2(3n + 10)\)
On December 7, Toys R Fun purchased $1,000 of merchandise with terms of 2/10, n/30. If payment is made on December 30, demonstrate the required journal entry for Toys R Fun to record the payment under the perpetual inventory system.
Answers
The correct option b. Debit Accounts Payable $1,000; Credit Cash $980; Credit Merchandise Inventory $20, is the required journal entry for Toys R Fun.
Explain the term Credit Merchandise Inventory?Merchandise inventory serves as a holding account of inventory that is awaiting sale as a current asset. Since there is a typical debit balance, debit grows while credit shrinks.For the stated question;
Toys R Fun is offered a discount of two percent if he settles within 10 days as well as the payable is required in 30 days, as indicated by the terms "2/10,n/30."
$20 (2 percent of $1,000) is the result.
On the 17th, which falls inside the discount days, the payment for the journal entry for Toys R Fun is:
$1,000 - Dr. Accounts Payable
Cr money - $980
$20 worth of Cr inventory.
Let's say, however, that the payment is made by December 30 rather than that day.
The submission will be:
$1,000 Dr. Accounts Payable.
$1,000 cash in Cr.
To know more about the Credit Merchandise Inventory, here
https://brainly.com/question/24074118
#SPJ4
The complete question is-
On Dec. 7, Toys R Fun purchased $1,000 of merchandise with terms of 2/10,n/30. If payment is made on December 30, demonstrate the required journal entry for Toys R Fun to record the payment under the perpetual inventory system.
a. Debit Cash $1,000; Credit Accounts Payable $1,000
b. Debit Accounts Payable $1,000; credit Cash $980; credit Merchandise Inventory $20.
c. Debit Accounts Payable $1,000; credit Cash $1,000
The state medical school has discovered a new test for tuberculosis. (If the test indicates a person has tuberculosis, the
test is positive.) Experimentation has shown that the probability of a positive test is 0.79, given that a person has
tuberculosis. The probability is 0.08 that the test registers positive, given that the person does not have tuberculosis.
Assume that in the general population, the probability that a person has tuberkulosis is 0.05. What is the probability that a
person chosen at random will fall in the following categories. (Enter your answers to four decimal places.)
(a) have tuberculosis and have a positive test
(b) not have tuberculosis
(c) not have tuberculosis and have a positive test
Answers
The probability according to the given scenario is:
(a) 0.0395
(b) 0.95
(c) 0.076
The given values are:
\(P(B/A) = 0.79\)\(P(A) = 0.05\)(a)
The probability that the b/w has tuberculosis as well as having (+) test will be:
→ \(P(A \cap B) = P(B/A).P(A)\)
By substituting the values, we get
→ \(= 0.79\times 0.05\)
→ \(= 0.0395\)
(b)
The probability that a person does not have tuberculosis will be:
→ \(P(A') = 1-P(A)\)
→ \(=1-0.05\)
→ \(= 0.95\)
(c)
The person does not have tuberculosis as well as have a (+) test, the probability will be:
→ \(P(A' \cap B) = P(A').P(B/A')\)
→ \(= 0.95\times 0.08\)
→ \(= 0.076\)
Learn more:
https://brainly.com/question/14816227
Type the correct answer in each box. Lmk!

Answers
There were 0-5 Listeners when the song was released.
The approximate number of listeners who had heard the song after the hour 5 was 15- below 50
The number of listeners was about 29,458 after hour 5842.62/
How can I explain?Alternative forms
Y= 4,637(1.26)ˣ
292131/50,5842,31/50,5.84262 =10³
5842.62
Including polynomial components, such as squared or cubed predictors, is the most popular technique to fit curves to data using linear regression. Typically, the model order is determined by the number of bends required in your line. Each exponent increment causes one additional bend in the curved fitting line.
Curve of Best Fit: a scatter plot curve that best approximates the trend. If the data looks to be quadratic, we use quadratic regression to get the equation for the best-fit curve. We do a cubic regression if it looks to be cubic.
To learn more about scatter plot graph to refer:
brainly.com/question/28151720
#SPJ1
Are the triangles congruent?? PLS HELP ME THANKS!
You have to pick SSS, SAS, ASA, AAS, or not congruent (none). (A=Angle, S=Side)
I can do the last part if you tell me the beginning of the question! THANKS

Answers
Answer:
yes, they are by SSS
Step-by-step explanation:
EF=AB
ED=BC
DF=AC
therefore, both triangles are congruent
i need help!!!! does anyone know this..!!???

Answers
The period of oscillation is 3 seconds
What is period of oscillation?A Oscillation is the periodic change of a measure around a central value or between two or more states, usually in time.
The time taken for an oscillating particle to complete one cycle of oscillation is known as the Period of oscillating particle. It is measured in seconds
Oscillation can also be vibration or revolution or cycle.
Therefore, using the graph to determine the period. Then the wave particle made a complete oscillation at 3 second.
This means that the period of the particle is 3 seconds.
learn more about period of oscillation from
https://brainly.com/question/22499336
#SPJ1
\(\int\limits^5_1 {x^2+2x-tanx} \, dx\)
Answers
The definite integral for this problem has the result given as follows:
\(\int_1^5 x^2 + 2x - \tan{x} dx = 212 - \ln{|\sec{5}|} + \ln{|\sec{1}|}\)
How to solve the definite integral?The definite integral for this problem is defined as follows:
\(\int_1^5 x^2 + 2x - \tan{x} dx\)
We have an integral of the sum, hence we can integrate each term, and then add them.
For the first two terms, applying the power rule, the integrals are given as follows:
Integral of x² = x³/3.Integral of 2x = 2x²/2 = x².The integral of the tangent is given as follows:
ln|sec(x)|
Then the integral is given as follows:
I = x³/3 + x² - ln|sec(x)|, from x = 1 to x = 5.
Applying the Fundamental Theorem of Calculus, the result of the integral is obtained as follows:
I = 5³/3 + 5² - ln|sec(5)| - (1³/3 + 1² - ln|sec(1)|)
I = 625/3 - 1/3 + 5 - 1 - ln|sec(5)| + ln|sec(1)|
I = 208 + 5 - 1 - ln|sec(5)| + ln|sec(1)|
I = 212 - ln|sec(5)| + ln|sec(1)|.
More can be learned about definite integrals at https://brainly.com/question/22008756
#SPJ1
Which graph represents a function?

Answers
Answer:
The question asks us to identify which of the provided graphs represents a function.
A relationship can be called a function only if one x-value corresponds to exactly one y-value.
To know if a relationship is a function from its graph, we can use something called the vertical line test. This is where you draw (or imagine) a vertical line going through the graph. If the line touches the curve exactly once, it passes the test and is a function.
In this question, for the first option, if we imagine a vertical line going through the graph, we can see that it touches the graph continuously at x = 1. Therefore, it is not a function.
Similarly, for the second and third options, the vertical lines would touch the graph twice. Therefore, they aren't functions either.
Finally, for the last option, we can see that a vertical line would touch the graph exactly once at every value of x. Therefore, it is a function.
Find the area of the triangle having the indicated angle and sides. (Round your answer to one decimal place.)
B 128°, a 86, c = 37

Answers
The area of the triangle with angle B = 128°, side a = 86, and side c = 37 is approximately 2302.7 square units.
To find the area of a triangle when one angle and two sides are given, we can use the formula for the area of a triangle:
Area = (1/2) * a * b * sin(C),
where a and b are the lengths of the two sides adjacent to the given angle C.
In this case, we have angle B = 128°, side a = 86, and side c = 37. To find side b, we can use the law of cosines:
c² = a² + b² - 2ab * cos(C),
where C is the angle opposite side c. Rearranging the formula, we have:
b² = a² + c² - 2ac * cos(C),
b² = 86² + 37² - 2 * 86 * 37 * cos(128°).
By substituting the given values and calculating, we find b ≈ 63.8.
Now, we can calculate the area using the formula:
Area = (1/2) * a * b * sin(C),
Area = (1/2) * 86 * 63.8 * sin(128°).
By substituting the values and calculating, we find the area of the triangle to be approximately 2302.7 square units.
For more question on area visit:
https://brainly.com/question/2607596
#SPJ8
Isaac takes a 216-mile trip from
Boston to New York City. He drives
at a rate of 54 miles per hour. The
equation d = 54t models his
distance, d, over time ,t, in hours. Complete the table of values and identify the independent and variables.
Independent input -Time “0,1,2,3,4”
Dependent output- distance
“0,__,180,__,216”
*Fill in the blank*
WRONG ANSWERS GET REPORTED!!!
Answers
Answers:
First Blank = 54Second Blank = 162=============================================
Explanation:
The first blank represents the distance that corresponds to t = 1 hour.
We'll replace t with 1 to get...
d = 54t
d = 54*1
d = 54
Therefore, 54 goes in the first blank. It means that Isaac traveled 54 miles after 1 hour.
------------------
We repeat these steps for t = 3
d = 54*t
d = 54*3
d = 162
This means he traveled 162 miles after 3 hours
So 162 goes in the second blank
-------------------
Side note: your teacher wrote 180 but s/he should have written 108 instead because 54*2 = 108
Find the measure of BC

Answers
Using central angle theorem,
The measure of the arc BC = 110°.
Define central angle?An angle with its vertex in the middle of the circle it creates with its two radii is said to be central.
Here in the question,
As per the central angle theorem:
(2x -30) ° + x° = 180°
⇒ 2x - 30 + x = 180
⇒ 3x - 30 = 180
Adding 30 on both sides:
⇒ 3x = 180 + 30
⇒ 3x = 210
Dividing both sides by 3.
⇒ x = 70°
Now BC = 2x-30
= 2 × 70 -30
= 140 - 30
= 110°
Therefore, the measure of BC = 110°.
To know more about central angle, visit:
https://brainly.com/question/15698342
#SPJ1
this is high school math one both of these questions can you tell me if they are a function or not and why

