Choose all options that apply . Which of the following are steps necessary to ensure patient safety ? a) Make sure that the medication is dispensed in the same units in which it was prescribed. b ) Review any calculation questions with the pharmacist . Check to see if there's a better medication for the patient's problem. d) Dispense an extra dose to save the patient from having to return in case of loss or damage to one of the doses. Oe ) Compare the label on the medication with the order from the physician .
Answers

Related Questions
Suppose we take a poll (random sample) of 3923 students classified as Juniors and find that 3196 of them believe that they will find a job immediately after graduation. What is the 99 % confidence interval for the proportion of GSU Juniors who believe that they will, immediately, be employed after graduation.
Answers
Answer:
The 99% confidence interval for the proportion of GSU Juniors who believe that they will, immediately, be employed after graduation is (0.7987, 0.8307).
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
Suppose we take a poll (random sample) of 3923 students classified as Juniors and find that 3196 of them believe that they will find a job immediately after graduation.
This means that \(n = 3923, \pi = \frac{3196}{3923} = 0.8147\)
99% confidence level
So \(\alpha = 0.01\), z is the value of Z that has a p-value of \(1 - \frac{0.01}{2} = 0.995\), so \(Z = 2.575\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.8147 - 2.575\sqrt{\frac{0.8147*0.1853}{3923}} = 0.7987\)
The upper limit of this interval is:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.8147 + 2.575\sqrt{\frac{0.8147*0.1853}{3923}} = 0.8307\)
The 99% confidence interval for the proportion of GSU Juniors who believe that they will, immediately, be employed after graduation is (0.7987, 0.8307).
write each rate as a fraction in lowest terms 20 feet in 40 seconds
Answers
Answer:
1/2 feet per second.
Step-by-step explanation:
Is this A,B,C or D helppppp

Answers
Answer:
D
Step-by-step explanation:
D goes thru positive 4 and negative 3
10. Convert 102°F to °C using this equation: C = 5(F-32)
Round to the nearest tenth.
9
Answers
Is the answer
Answer:
38.9 degrees C
Step-by-step explanation:
Use the equation:
\(C=\frac{5}{9} (F-32)\)
to convert degrees Fahrenheit to degrees Celsius. So replace the value for the Fahrenheit with 102 and solve for C:
\(C=\frac{5}{9} (F-32)\\C=\frac{5}{9} (102-32)\\C=\frac{5}{9} (70)\\C=\frac{350}{9} \approx38.89\,^oC\)
which to the nearest tenth can be written as: 38.9 degrees C
3/2 equals 4x x=
?????
Answers
Answer:
0.375
Step-by-step explanation:
3/2 equals 1 and a half, and 1 and a half divided by 4 will get you 0.325
Answer:
4x - 2 = 3x + 1. Solution We substitute the value 3 for x in the equation and see if the left-hand member equals the right-hand member. 4(3) - 2 = 3(3) + 1.
Suppose you want to test the claim that μ>25.6. Given a sample size of n=42 and a level of significance of α=0.025, when should you reject the null hypothesis?
A. if the standardized test statistic is greater than 1.96
B. if the standardized test statistic is greater than 1.28
C. if the standardized test statistic is greater than 2.33
D. if the standardized test statistic is greater than 1.65
Answers
If the test statistic is higher than 1.645, reject H0. If the test statistic is higher than 2.33, reject H0.
What is null hypothesis?Conjectures used in statistical tests, which are formal techniques for drawing conclusions or making judgments based on data, include the null hypothesis and the alternative hypothesis.
The hypotheses, which are based on a sample of the population, are suppositions regarding a statistical model of the population.
The tests are essential components of statistical inference and are frequently used to distinguish between statistical noise and scientific claims when interpreting experimental data in science.
"The null hypothesis is the proposition under investigation in a statistical significance test.
The significance test is intended to determine how strong the evidence is against the null hypothesis. The null hypothesis is typically a claim that there is "no effect" or "no difference.
H0 is a common way to represent it.
Hence, If the test statistic is higher than 1.645, reject H0. If the test statistic is higher than 2.33, reject H0.
learn more about null hypothesis click here:
https://brainly.com/question/13776238
#SPJ1
Create an expression that has the same value as (6x-4) + (x + 5).
Write the correct numbers from the list in the blank boxes. Each number
may be used once, more than once, or not at all.
Answers
Answer: 7x + 1
Step-by-step explanation:
(6x-4)+(x+5)
Step 1: Remove Parentheses:
6x-4+x+5
Step 2: Combine Like Terms:
7x +1
Hi can any one teach me this constant difference

Answers
The constant differences between the consecutive terms are 2 (a); 2 (b), -3 (c), 7 (d), 1(e), and 6(f).
How do you find the constant difference in a sequence of numbers?In math, the constant difference can be defined as the number that defines the pattern of a sequence of numbers. This means that number that should be added or subtracted to continue with the sequence.
Due to this, to determine the constant difference it is important to observe the pattern and find out the number that should be added. For example, if the sequence is 2, 4, 6, 8, there is a difference of 2 between each of the numbers and this is the constant difference.
Learn more about numbers in https://brainly.com/question/24908711
#SPJ1
Please help if you can

Answers
1) The lower limit of the confidence Interval is: 1489.77.
The upper limit of the confidence Interval is: 1530.23
2) The lower limit of the confidence Interval is: 1478.32
The upper limit of the confidence Interval is: 15411.68
How to find the confidence Interval?The formula to find the confidence interval is:
CI = x' ± z(σ/√n)
where:
CI is confidence interval
x' is sample mean
z is z-score at confidence level
σ is standard deviation
n is sample size
1) The parameters are:
σ = $234
x' = $1510
n = 362
z at 90% CL = 1.645
Thus:
CI = 1510 ± 1.645((234/√362)
CI = 1510 ± 20.23
CI = (1489.77, 1530.23)
2) The parameters are:
σ = $234
x' = $1510
n = 362
z at 99% CL = 2.576
Thus:
CI = 1510 ± 2.576((234/√362)
CI = 1510 ± 31.68
CI = (1478.32, 15411.68)
Read more about Confidence Interval at: https://brainly.com/question/15712887
#SPJ1
Jackson is making brownies. He uses the following ingredients.
Ingredients Amount for 1
Batch of Brownies
Flour 3 cups
Sugar 2 cups
Butter 1/3 cup
Cocoa Powder 1/4 cup
Jackson has 1 cup of butter. If he wants to use all the butter, how many batches of brownies can he make?
Part A
Which equation can you use to solve the problem?
A. 1 ÷ 3 = 3
B. 1 ÷ 13 = 3
C. 1 × 13 = 13
D. 1 + 13 = 13
Part B
Jackson used all the butter to make the brownies.
If each brownie is 1/9 of a batch, how many brownies did he make?
Enter your answer in the box.
Answers
Answer:
It's B (1÷13=3) for Part a
1 whole is equal to 3/3. One batch of brownies uses up to 1/3 of butter. So 1 ÷ 1/3 = 3.
Step-by-step explanation:
in a study, the data you collect is age (in years). What is the level of measurement?
Answers
Answer:
nominal ordinal interval ratio
Step-by-step explanation:
there
What is the inverse of the function f(x)= -1/2 (x+3)
Answers
Answer:
-2x-3
Step-by-step explanation:
See the image below:) you can use the app photo math, you just take a picture of the problem and it gives you the answer and explains the steps.

URGENT!!! Find the surface area of the regular pyramid to the nearest hundredth.

Answers
Answer:
632.83mm²
Step-by-step explanation:
Applying Pythagorean theorem to triangle SOH
SH² = SO² + OH²
SH = \(\sqrt{(15.4)^2+(7.2)^2}=17mm\)
Since the base of the pyramid is a regular pentagon, angle OAH
is 108°/2 = 54°.
AH = 7.2/tan 54° = 5.23mm
So AB = 2AH = 10.46mm
The area of triangle SAB is:
A1 = 1/2 × SH × AB = 1/2 × 17 × 10.46 = 88.91mm²
The area of all triangles is
A2 = 5 × A1 = 5 × 88.91 = 444.55mm²
The area of the base is:
A3 = (perimeter × apothem)/2 = (5 × 10.46 × 7.2)/2 = 188.28mm²
The surface area of the pyramid is:
A2 + A3 = 444.55 + 188.28 = 632.83mm²

Step-by-step explanation:
the surface area is the sum of the base area (pentagon) and the 5 side triangles (we only need to calculate one and then multiply by 5, as they are all equal).
these side triangles are isoceles triangles (the legs are equally long).
the usual area formula for a pentagon is
1/2 × perimeter × apothem
the apothem is the minimum distance from the center of the pentagon to each of its sides.
in our case this is 7.2 mm.
how to get the perimeter or the length of an individual side of the pentagon ?
if the apothem of a pentagon is given, the side length can be calculated with the formula
side length = 2 × apothem length × tan(180/n)
where 'n' is the number of sides (5 in our case). After getting the side length, the perimeter of the pentagon can be calculated with the formula
perimeter = 5 × side length.
so, in our case
side length = 2 × 7.2 × tan(180/5) = 14.4 × tan(36) =
= 10.4622124... mm
perimeter = 5 × 10.4622124... = 52.31106202... mm
area of the pentagon = 1/2 × perimeter × apothem =
= 1/2 × 52.31106202... × 7.2 = 188.3198233... mm²
now for the side triangles.
the area of such a triangle is
1/2 × baseline × height
baseline = pentagon side length
height we get via Pythagoras from the inner pyramid height and the apothem :
height² = 7.2² + 15.4² = 51.84 + 273.16 = 289
height = 17 mm
area of one side triangle =
1/2 × 10.4622124... × 17 = 88.92880543... mm²
all 5 side triangles are then
444.6440271... mm²
and the total surface area is then
444.6440271... + 188.3198233... = 632.9638504... mm²
≈ 632.96 mm²
Can someone please help me asap, This is overdue and i need to get it done and im very confused... !! ILL GIVE BRAINLIST !!


Answers
Answer:
Below
Step-by-step explanation:
At B ( 40 mins) and D (30 mins) he is not moving....visiting .
The width of A is the time it took to get to first house = 20 mins
The width of C is t the time to get to second house = 60 to 70 = 10 mins
Riding toward home at C and E ( the distance...the y-value....is getting less)
He is fastest where the line has greatest slope...where it is steepest = C
He was away from home the width of the graph = 115 mins
Which equation has the solution x = 5? Select each correct answer. Responses x5+5=6 x over 5 end fraction plus 5 equals 6 25x+4=9 25 over x end fraction plus 4 equals 9 32−4x=12 32 minus 4 x equals 12 11 + 6x = 22 11 + 6, x, = 22 3x + 1 = 9 3, x , + 1 = 9 18−2x=9
Answers
The equations that have the solution x = 5 are 25/x + 4 = 9 and 32 − 4x = 12
How to determine the equationFrom the question, we have the following parameters that can be used in our computation:
x⁵ + 5 = 6
25/x + 4 = 9
32 − 4x = 12
11 + 6x = 22
3x + 1 = 9
18 − 2x = 9
Solving each equation, we have
Equation 1: x⁵ + 5 = 6
Evaluate the like terms
x⁵ = 1
Take the fifth-root
x = 1
Equation 2: 25/x + 4 = 9
Evaluate the like terms
25/x = 5
So, we have
5x = 25
Divide by 5
x = 5
Equation 3: 32 − 4x = 12
Evaluate the like terms
4x = 20
Divide by 4
x = 5
Equation 4: 11 + 6x = 22
Evaluate the like terms
6x = 11
Divide by 4
x = 11/6
Equation 5: 3x + 1 = 9
Evaluate the like terms
3x = 8
Divide by 3
x = 8/4
Equation 6: 18 − 2x = 9
Evaluate the like terms
2x = 9
Divide by 2
x = 9/2
Hence, the equations are 25/x + 4 = 9 and 32 − 4x = 12
Read more about equations at
https://brainly.com/question/2476251
#SPJ1
Consider the line 3x+2y=-1.
Find the equation of the line that is perpendicular to this line and passes through the point (5, 3).
Find the equation of the line that is parallel to this line and passes through the point (5, 3).
Note that the ALEKS graphing calculator may be helpful in checking your answer.
Equation of perpendicular line:
Equation of parallel line:
0
Answers
The given line is in the form Ax + By = C, where A = 3, B = 2, and C = -1. To find the slope of this line, we can rearrange the equation in slope-intercept form (y = mx + b), where m is the slope:
3x + 2y = -1
2y = -3x - 1
y = (-3/2)x - 1/2
The slope of the given line is -3/2. Since a line perpendicular to this line will have a negative reciprocal slope, we can find the perpendicular slope by taking the negative reciprocal of -3/2:
Perpendicular slope = -1 / (-3/2) = 2/3
Now we have the slope of the perpendicular line, and we can use the point-slope form of a line (y - y₁ = m(x - x₁)) to find its equation. Plugging in the values (5, 3) for (x₁, y₁) and 2/3 for m:
y - 3 = (2/3)(x - 5)
Expanding and simplifying:
3y - 9 = 2x - 10
2x - 3y = 1
Therefore, the equation of the line that is perpendicular to 3x + 2y = -1 and passes through the point (5, 3) is 2x - 3y = 1.
To find the equation of a line parallel to the given line and passing through the point (5, 3), we can use the same method. Since parallel lines have the same slope, the slope of the parallel line will also be -3/2.
Using the point-slope form with (5, 3) and -3/2:
y - 3 = (-3/2)(x - 5)
Expanding and simplifying:
2y - 6 = -3x + 15
3x + 2y = 21
Therefore, the equation of the line that is parallel to 3x + 2y = -1 and passes through the point (5, 3) is 3x + 2y = 21.
I need this answered quick. What sum is represented by the following number line?

Answers
Answer:
2\(\frac{3}{4} + -4\frac{1}{4} = -1\frac{2}{4}\)
Step-by-step explanation:
The initial position of the blue line is 2 and 3/4. The final position (represented by the red line) is -1 and 1/2. 2 and 3/4 - 4 and 1/4 is the only thing you can subtract to get -1 and 2/4.
Answer:
2 3/4 +(-3 1/4)= -1 2/4
Step-by-step explanation:
hope you get it right
Two wires are attached to a pole and create similar triangles with the ground. The longer wire is attached to the ground 32 feet from
the base of the pole and the shorter wire is attached to the ground 16 feet from the base of the pole.
If the cosine of the angle formed by the shorter wire and the ground is 8/41, what is the length of the longer wire?
Please help im so confused!
Answers
The length of the longer wire is 82 feet.
Let's denote the length of the longer wire as L. According to the given information, the shorter wire is attached to the ground 16 feet from the base of the pole, and the longer wire is attached to the ground 32 feet from the base of the pole.
We can form two similar right triangles using the wires. The height of each triangle is the height of the pole, and the base of each triangle is the distance from the base of the pole to where the wire is attached to the ground.
In the first triangle, the shorter wire creates an angle with the ground. Let's denote this angle as θ. Since we are given the cosine of this angle, we can use the cosine function to find the height of the pole in terms of θ and the base of the triangle:
cos(θ) = adjacent/hypotenuse = 16/L
Given that cos(θ) = 8/41, we can substitute this value into the equation:
8/41 = 16/L
To solve for L, we can cross-multiply and solve for L:
8L = 41 * 16
L = (41 * 16)/8
L = 82
Therefore, the length of the longer wire is 82 feet.
In summary, the length of the longer wire is 82 feet, as determined by using the cosine of the angle formed by the shorter wire and the ground, and considering the similarity of the triangles formed by the wires and the pole.
For more such questions on length visit:
https://brainly.com/question/28322552
#SPJ8
Which is true about the solution to the system of inequalities shown? y > 3x + 1 y < 3x – 3 On a coordinate plane, 2 solid straight lines are shown. The first line has a positive slope and goes through (negative 2, negative 5) and (0, 1). Everything to the left of the line is shaded. The second line has a positive slope and goes through (0, negative 3) and (1, 0). Everything to the right of the line is shaded. Only values that satisfy y > 3x + 1 are solutions. Only values that satisfy y < 3x – 3 are solutions. Values that satisfy either y > 3x + 1 or y < 3x – 3 are solutions. There are no solutions.
Answers
There are no solutions to the system of inequalities Option (d)
Inequalities are a fundamental concept in mathematics and are commonly used in solving problems that involve ranges of values.
A system of two inequalities is a set of two inequalities that are considered together. In this case, the system of inequalities is
y > 3x + 1
y < 3x - 3
The inequality y > 3x + 1 represents a line on the coordinate plane with a slope of 3 and a y-intercept of 1. The inequality y < 3x - 3 represents another line on the coordinate plane with a slope of 3 and a y-intercept of -3. We can draw these lines on the coordinate plane and shade the regions that satisfy each inequality.
The first line has a positive slope and goes through (negative 2, negative 5) and (0, 1). Everything to the left of the line is shaded. The second line has a positive slope and goes through (0, negative 3) and (1, 0). Everything to the right of the line is shaded.
We can start by analyzing the inequality y > 3x + 1. This inequality represents the region above the line with a slope of 3 and a y-intercept of 1. Therefore, any point that is above this line satisfies this inequality.
Next, we analyze the inequality y < 3x - 3. This inequality represents the region below the line with a slope of 3 and a y-intercept of -3. Therefore, any point that is below this line satisfies this inequality.
To determine which values satisfy both inequalities, we need to find the region that satisfies both inequalities. This region is the intersection of the regions that satisfy each inequality.
When we analyze the regions that satisfy each inequality, we see that there is no region that satisfies both inequalities. Therefore, there are no values that satisfy the system of inequalities shown.
There are no solutions to the system of inequalities y > 3x + 1 and y < 3x - 3 by analyzing the regions that satisfy each inequality on a coordinate plane. The lack of a solution is determined by the fact that there is no region that satisfies both inequalities.
To know more about Inequalities here
https://brainly.com/question/28823603
#SPJ1
Complete Question :
Which is true about the solution to the system of inequalities shown?
y > 3x + 1
y < 3x – 3
On a coordinate plane, 2 solid straight lines are shown. The first line has a positive slope and goes through (negative 2, negative 5) and (0, 1). Everything to the left of the line is shaded. The second line has a positive slope and goes through (0, negative 3) and (1, 0). Everything to the right of the line is shaded.
Options:
a)Only values that satisfy y > 3x + 1 are solutions.
b)Only values that satisfy y < 3x – 3 are solutions.
c)Values that satisfy either y > 3x + 1 or y < 3x – 3 are solutions.
d)There are no solutions.
Answer:
D
Step-by-step explanation:
Help (ಥ‿ಥ)
Factor the perfect square trinomial 25x2 - 60x + 36.
A. (5x – 4)(5x-9)
B. (5x-6)2
C. (5x - 3)2
D. (5x - 12)(5x - 3).
Answers
Answer: B
Step-by-step explanation:
PLEASE HELP ME FAST!!!!!
Below are the data collected from two random samples of 500 American adults on the number of hours they work per day (rounded to the nearest hour):
Number of hours of work per day 6 7 8 9 10
Sample A: Number of adults 60 90 145 150 55
Sample B: Number of adults 70 80 140 145 65
Ryan concludes that adults spend a mean of 8 hours working each day. Malia thinks the mean is 9 hours. Who is correct—Ryan or Malia? Explain your answer in two or three sentences. Make sure to use facts to support your answer. (10 points)
Answers
The average number of hours that adults spend working each day is 8 hours and Ryan is correct because he got the average of 8 right.
We know that,
The sample mean is a statistic that is computed by taking the arithmetic mean of the values of a variable in a sample. If the sample is taken from probability distributions with a shared expected value, the sample mean is an estimator of that value.
The mean is gotten from the formula;
x' = ∑x/n
Number of hours of work per day are; 6, 7, 8, 9 and 10
Thus; sum up all of it
∑x = 6 + 7 + 8 + 9 + 10
∑x = 40
Mean is; x' = 40/5
x' = 8
Since Ryan concluded that the average is 8 hours,
Therefore,
We can say that Ryan is correct.
Read more about mean of data at;
brainly.com/question/24245867
#SPJ1
determine the equation of the parabola that opens up, has vertex (7,7) and a focal diameter of 16.
Answers
The equation of a parabola that opens up and has a vertex at (7,7) can be written in the form
y = a(x - 7)^2 + 7.The focal diameter of the parabola is 16, which means that the distance from the vertex to the focus is 8 (since the focal diameter is the sum of the distances from the vertex to the focus and from the vertex to the directrix).
To find the equation of the parabola, we need to determine the value of a that will give us the correct focal diameter. The distance from the vertex to the focus is given by the equation sqrt(4a(y - 7)), so we can set this equal to 8 and solve for a:
sqrt(4a(y - 7)) = 8
4a(y - 7) = 64
a(y - 7) = 16
a = 16 / (y - 7)
Substituting this value of a back into the equation for the parabola gives us:
y = (16 / (y - 7))(x - 7)^2 + 7
This is the equation of the parabola that opens up, has a vertex at (7,7), and a focal diameter of 16.
Learn more about focal diameter here:
https://brainly.com/question/27357773
#SPJ4
A game Is played using one die. If the die is rolled and shows 3, the player wins $15. M the die shows any number other than 3, the player wins nothing. Complete parts (a) through (0)
a. If there is a charge of $3 to play the game, what is the game's expected value?
Answers
Answer:
0
Step-by-step explanation:
Expected Value = (Probability of winning) x (Amount won) + (Probability of losing) x (Amount lost)
In this case, the probability of winning is 1/6 (since there is only one way to roll a 3 out of six possible outcomes), and the probability of losing is 5/6 (since there are five other outcomes that do not result in a win).
The amount won is $15, and the amount lost (i.e., the cost of playing the game) is $3.
Therefore, the expected value is:
Expected Value = (1/6) x $15 + (5/6) x (-$3)
Expected Value = $2.50 - $2.50
Expected Value = $0
I need help with this question

Answers
Using word problems and equations, Sarah worked for 10 hours and Penelope worked for 5 hours
What is the number of hours Sarah and Penelope worked?This is a word problem and in order to solve this, we need to translate mathematical statements in form of word problems into mathematical equations.
Let's assume that Sarah worked x hours.
Given that Sarah can iron 30 shirts per hour, the total number of shirts she ironed is 30x.
Since Penelope worked half the hours of Sarah, Penelope worked x/2 hours.
Given that Penelope can iron 35 shirts per hour, the total number of shirts she ironed is 35 * (x/2) = (35/2)x.
The total number of shirts ironed by both Sarah and Penelope is 475 shirts.
So, we can write the equation: 30x + (35/2)x = 475.
To solve this equation, we can simplify it: (60/2)x + (35/2)x = 475, which becomes (95/2)x = 475.
Now, we can solve for x: x = (475 * 2) / 95 = 10.
Therefore, Sarah worked 10 hours and Penelope worked half of that, which is 5 hours.
learn more on word problems here;
https://brainly.com/question/13818690
#SPJ1
It says to find the surface area of each figure. Round to the nearest hundredth. Please help!
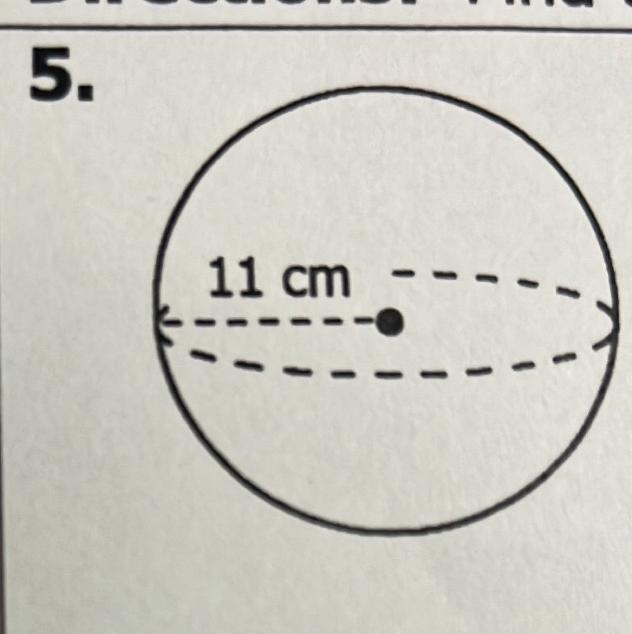
Answers
SOLUTION
The figure given is a sphere, and we want to find the surface area. The diameter of the sphere has been given as 11 cm.
Surface area of a sphere is found using the formula
\(\begin{gathered} S.A=4πr^2 \\ where\text{ r = radius = }\frac{diameter}{2}=\frac{11}{2}=5.5 \end{gathered}\)Putting in the values of pi and radius r into the formula, we have the surface area S.A as
\(\begin{gathered} S.A=4πr^2 \\ =4\times\pi\times5.5^2 \\ =380.13271108\text{cm}^2 \end{gathered}\)Hence the answer is 380.13 square-centimeter to the nearest hundredth
You make an investment of $2250.00 with an absolute change of ―$350.00. What is your investment now
worth and what was the percent change?
Answers
1. The investment of $2,250 with an absolute change of -$350 is now worth $1,900.
2. The percentage change in the worth of the investment is -15.56%.
What is a percentage change?A percentage change refers to the percentage difference between the initial value and the current value.
To compute the percentage change, use the absolute change and divide by the initial value, then multiply by 100.
For this investment of $2,250 which is now worth $1,900, there was a percentage change of -15.56%, implying that it has drastically reduced in value.
Initial Investment Cost = $2,250.00
Absolute change in investment value = $350
Current value of investment = $1,900 ($2,250 + $350)
The percentage change = -15.56% (-$350/$2,250 x 100)
Thus, the investment is currently valued at $1,900, having lost $350 in value, which in percentage terms, is -15.56%.
Learn more about percentage changes at https://brainly.com/question/809966
#SPJ1
Verify that f and g are inverses functions using composition , show your steps

Answers
Answer:
See explanations below
Step-by-step explanation:
Given the functions
f(x) = 12x - 12
g(x) = x/12 - 1
To show they are inverses, we, must show that f(g(x)) = g(f(x))
f(g(x)) = f(x/12 - 1)
Replace x with x/12 - 1 into f(x)
f(g(x)) =12((x-12)/12) - 11
f(g(x)) = x-1 - 1
f(g(x)) =x - 2
Similarly for g(f(x))
g(f(x)) = g(12x-12)
g(f(x)) =(12x-12)/12 - 1
12(x-1)/12 - 1
x-1 - 1
x - 2
Since f(g(x)) = g(f(x)) = x -2, hence they are inverses of each other
What’s the measure of x for the for each figure?

Answers
Answer:
a)73
b)27
c)58
d)70
According to your graphing calculator, what is the approximate solution to the trigonometric inequality cos(0.65x)>.44 over the interval 0
Answers
Answer:
the solution to the trigonometric inequality cos(0.65x) > 0.44 over the interval 0 ≤ x < 4.834.
Step-by-step explanation:
The given inequality is:
cos(0.65x) > 0.44
To solve this inequality, we need to isolate the variable x.
First, let's take the inverse cosine (arccos) of both sides to remove the cosine function:
arccos(cos(0.65x)) > arccos(0.44)
Since the range of the inverse cosine function is limited to [0, π], we can rewrite the inequality as:
0 ≤ 0.65x < π
Now, let's solve for x by dividing each part of the inequality by 0.65:
0/0.65 ≤ x < π/0.65
Simplifying, we have:
0 ≤ x < π/0.65
Now, let's calculate the approximate value of π/0.65 to determine the interval for x:
π/0.65 ≈ 4.834
i hope i helped!
(100 POINTS AND BRAINLYEST)
(SOLVE ALL)
24.2 miles above
2. The line of site to the horizon would be tangent to the Earth’s surface. What kind of angle is formed between the radius of the Earth and the line of site? (1 point)
3. You will be setting up a right triangle to solve this problem using the radius of the Earth (3,959 miles), the distance to the horizon (which is unknown), and the altitude of Felix. Sketch and image of this scenario. Include distances on the right triangle. (3 points)
4. Use the Pythagorean Theorem to find the distance from Felix in the image to the horizon. (3 points)
5. Standing on the ground, the surface of the Earth appears to be flat. How far would a person on the ground have to travel to get a point on the horizon that Felix could see. Sketch a right triangle of this scenario using the altitude of Felix, the distance to the horizon, and the distance on the ground to the horizon (which is unknown). Include distances on the right triangle. Use the Pythagorean Theorem to find the missing side of the triangle. (5 points)
6. Use the answer from number 5 to determine the central angle of the Earth that Felix is viewing from his altitude. Treat the answer from number 5 like an arc length. You will need to use the radius of the Earth in this problem. Answer in radians or degrees. (2 points)
Answers
The analysis of the distances and angles viewed by Felix are presented as follows;
2. The angle formed is a right angle
3. Please find the drawing of the scenario created with MS Word
4. The distance obtained using Pythagorean Theorem is about 438.53 miles
5. The distance the person travels is about 437.86 miles
6. The central angle Felix is viewing from his altitude is about 6.34°
What is the Pythagorean Theorem?The Pythagorean Theorem states that the square of the hypotenuse side of a right triangle is equivalent to the sum of the squares of the legs of the right triangle.
2. The angle formed by a tangent to a spherical surface, such as the Earth's approximately spherical surface and the radius of the sphere is a right angle.
Therefore;
The angle formed between the radius of the Earth and the tangential line of sight is a right angle3. The possible elevation of Felix above the Earth's surface, obtained from a similar question is; 24.214 miles
Therefore;
The legs of the right triangle are the radius of the Earth and the distance from Felix's to the point on the horizon.
The hypotenuse sum of Felix's altitude and the radius of the Earth
Please find attached the drawing of the scenario created with MS Word
4. Pythagorean Theorem indicates that the distance from Felix to the image on the horizon, d, can be obtained as follows;
d = √((3,959 + 24.214)² - 3,959²) ≈ 438.53
The distance from Felix to the image on the horizon is about 438.53 miles
5. The distance the person has to travel can be found as follows;
The surface of the Earth is assumed to be flat
The distance to the horizon from Felix is about 438.53 miles
The distance, l, the person on the ground has to travel is therefore;
l = √(438.53² - 24.214²) ≈ 437.86
The distance the person on the ground has to travel to get to a point on the horizon Felix could see is about 437.86 miles6. The central angle, θ, of the Earth that Felix is viewing, with an arc length of 437.86 miles can be found using the formula for finding the arc length of a sector of a circle as follows;
θ/360 × 2 × π × 3,959 ≈ 437.86
θ ≈ 437.86 × 360/(3,959 × 2 × π) ≈ 6.34°
The central angle Felix is viewing, θ ≈ 6.34°Learn more on Pythagorean Theorem here: https://brainly.com/question/28984815
#SPJ1
