(Combining Equations)What is the result of adding these two equations ? 2x + 3y = -5 5x - y = -12
Answers
7x +2y =-17 ..... Finally, answer
2x + 3y = -5
+
5x -y = -12
---------------------------
7x +2y = -17
Related Questions
Listed below is a table showing the number of employees. 20 years or older by gender in the United states
Answers
The total number of workers that were studied can be found to be 139,340,000.
The percent of workers unemployed would be 5. 4 %.
Percentage of unemployed men is 5. 6 % and unemployed women is 5. 1%.
How to find the employment figures ?Number of employed workers :
= 74,624,000 + 64, 716, 000
= 139,340,000
Percentage unemployed :
= ( 4, 209,000 + 3,314,000 ) / 139,340,000
= 5. 4 %
Percentage of unemployed men :
= 4,209,000 / 74,624,000
= 5.6 %
Percentage of unemployed women:
= 3,314,000 / 64, 716, 000
= 5. 1 %
Find out more on unemployment at https://brainly.com/question/13280244
#SPJ1
The full question is:
a. How many workers were studied?
b. What percent of the workers were unemployed?
c. Compare the percent unemployed for the men and the women.

chau made $270 for 18 hours of work. At the same rate, how many hours would he have to work to make $105
Answers
Answer:
7 hours
Step-by-step explanation:
here,
270/18=105/x
x=(105*18)/270
x=7
Chau made $270 for 18 hours of work. At the same rate, Therefore Chau would have to work 7 hours at the same rate to make $105.
To find out how many hours Chau would have to work to make $105 at the same rate, we can set up a proportion using the given information:
Let x be the number of hours Chau needs to work to make $105.
We know that Chau made $270 for 18 hours of work, so the rate of earnings per hour is:
Rate = Total earnings / Number of hours
Rate = $270 / 18 hours
Rate = $15 per hour
Now, we can set up the proportion:
$15 per hour = $105 / x hours
To find x, we can cross-multiply:
$15 × x = $105
Now, solve for x:
x = $105 / $15
x = 7 hours
So, Chau would have to work 7 hours at the same rate to make $105.
To know more about rate
https://brainly.com/question/119866
#SPJ2
Which of these is a unit rate?
A. $4 for a bucket of popcorn
B.$20 for 5 sandwiches
C. $30 for 2 concert tickets
D. $100 for 6 games
Answers
Answer:
b
Step-by-step explanation:
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
y=⅔x+4 written in standard form
Answers
Answer:
I think it is 2x-3y=-12 not sure but try it
Tom is 5 years older than his brother Ted. The sum of their ages is 51. What are their
ages? Tell me the explanation!!!
Answers
Answer:
no
Step-by-step explanation:
100 Points! Algebra question, photo attached. Please show as much work as possible. Thank you!

Answers
A. The distributions of the periods is that using the five number summary is that
The 7th Period has higher minimum and lower maximumThe 3rd period is more spread (from the quartiles)The 7th Period has higher medianB. The box and whisker plot of the periods is attached
A. Comparing the distributions of the periodsFrom the question, we have the following parameters that can be used in our computation:
7th Period
66, 72, 77, 78, 78, 80, 82, 84, 84, 87, 88, 88, 89, 89, 90 92, 92, 93, 94, 94 96, 96
3rd Period
52, 60, 62, 64, 64, 65, 68, 71, 72, 74, 75, 76, 78, 79, 83, 84, 85, 88, 89, 93, 94, 97
The distributions of the periods will be compared using the five-number summaries
Using a graphing tool, the five-number summaries are:
7th Period
Minimum: 66Lower Quartile Q1: 79.5Median: 88Upper Quartile Q3: 92.25Maximum: 963rd Period
Minimum: 52Lower Quartile Q1: 64.75Median: 75.5Upper Quartile Q3: 85.75Maximum: 97B. Creating a box and whisker plot of the periodsThe box and whisker plot of the periods is added as an attachment
From the box and whisker plot attached, we can see the five-number summaries of the periods
Read more about box plot at
https://brainly.com/question/3473797
#SPJ1

The population of Placerville grew from 4360 a decade ago to 6590 today.
Answers
Answer: To find the percent increase in population, I used the following formula:
percent increase = (new value - old value) / old value * 100
In this case, the old value was the population from a decade ago (4360), and the new value was the current population (6590). So plugging these values into the formula, we get:
percent increase = (6590 - 4360) / 4360 * 100
percent increase = 51.38%
So the population of Placerville increased by approximately 51.38% over the past decade. The population of Placerville has increased by (6590 - 4360) = 2230 people over the past decade.
Step-by-step explanation:
what is the value of (f-g)(2)

Answers
Answer:
Step-by-step explanation:
We need to find the value (f-g)(2), so we need first to substitute 2 into the given functions f(x) and g(x) and then subtract the result of g(2) from f(2).
Here, f(x) = 3x^2 + 1 and g(x) = 1 - x,
So, We will substitute 2 into these functions:
f(2) = 3(2)^2 + 1 = 3(4) + 1 = 12 + 1 = 13
g(2) = 1 - 2 = -1
Now, we can subtract g(2) from f(2):
(f-g)(2) = f(2) - g(2) = 13 - (-1) = 13 + 1 = 14
Hence, the required value of (f-g)(2) is 14.
Answer:
The correct answer is 3. To solve for g(-2), we substitute -2 for x in the equation g(x) = 2x + 5. This gives us g(-2) = 2(-2) + 5, which simplifies to -4 + 5 = 1. Next, we substitute the value of g(-2) into the equation for f(g(x)) = 4 - x^2. Thus, f(g(-2)) = 4 - (1)^2, which equals 4 - 1 = 3.
The product of three integers is −11. Determine all of the possible values for the three factors. Write each set of three factors in order from least to greatest. Make sure that each set uses unique integers. Listing the sets in a different order doesn't count.
Answers
Answer:
(-1, 1, 11), (-11, -1, -1), (-11, 1, 1)
Step-by-step explanation:
An integer is basically a whole number that can either be be zero, positive or negative.
Now, we are told that the product of three integers is −11.
The factors of 11 are 1 and 11
Thus;
The possible set of three factors that can give a product of -11 are;
(-1, 1, 11), (-11, -1, -1), (-11, 1, 1)
Triangles Q R S and X Y Z are shown. Angles Q S R and X Z Y are right angles. Angles Q R S and X Y Z are congruent. The length of Y Z is 9, the length of X Z is 12, and the length of hypotenuse X Y is 15.
Given △QRS ~ △XYZ, what is the value of tan(Q)?
Three-fifths
Three-fourths
Four-fifths
Answers
Answer:three-fourths
Step-by-step explanation:
because my dad said it was right
find an equation that passes through (1 ,2) and is parallel y=3x-9
Answers
Answer:
A line that is parallel to y = 3x - 9 will have the same slope as the given line. The slope of y = 3x - 9 is 3. Therefore, the equation of the line that passes through (1, 2) and is parallel to y = 3x - 9 is:
y - y1 = m(x - x1)
where m is the slope and (x1, y1) is the point (1, 2)
Substituting the values we get:
y - 2 = 3(x - 1)
Simplifying the equation we get:
y - 2 = 3x - 3
y = 3x - 1
Therefore, the equation of the line that passes through (1, 2) and is parallel to y = 3x - 9 is y = 3x - 1 .
;>
-3|x|+2x-1 is x=-5 brainly
Answers
Answer:
-3|x| + 2x - 1 evaluated at x = -5 is -26.
Step-by-step explanation:
To evaluate -3|x| + 2x - 1 at x = -5, we substitute -5 for x:
-3|-5| + 2(-5) - 1 = -3(5) - 10 - 1 = -15 - 10 - 1 = -26
Abby used the law of cosines for TriangleKMN to solve for k.
k2 = 312 + 532 – 2(31)(53)cos(37°)
Triangle K N M is shown. The length of K N is 53, the length of N M is k, and the length of K M is n.
Law of cosines: a2 = b2 + c2 – 2bccos(A)
What additional information did Abby know that is not shown in the diagram?
mAngleK = 37° and n = 31
mAngleK = 37° and k = 31
mAngleN = 37° and n = 31
mAngleN = 37° and k = 31
Answers
Answer:
m∠K = 37° and n = 31
Step-by-step explanation:
A lot of math is about matching patterns. Here, the two patterns we want to match are different versions of the same Law of Cosines relation:
a² = b² +c² -2bc·cos(A)k² = 31² +53² -2·31·53·cos(37°)ComparisonComparing the two equations, we note these correspondences:
a = kb = 31c = 53A = 37°Comparing these values to the given information, we see that ...
KN = c = 53 . . . . . . . . . . matching values 53NM = a = k . . . . . . . . . . . matching values kKM = b = n = 31 . . . . . . . matching values 31∠K = ∠A = 37° . . . . . . . matching side/angle namesAbby apparently knew that ∠K = 37° and n = 31.
__
Additional comment
Side and angle naming for the Law of Sines and the Law of Cosines are as follows. The vertices of the triangle are labeled with single upper-case letters. The side opposite is labeled with the same lower-case letter, or with the two vertices at either end.
Vertex and angle K are opposite side k, also called side NM in this triangle.
George has $3 in his saving account. He then adds $4 per day to the account. Let y represent the total amount in the account after x days.
Express the equation in the form of y=mx + b
Enter your answer in the box.
Plz help
Answers
Answer:
y = 4x + 3
Step-by-step explanation:
since we know how much he adds daily, we can put it next to 4, since we don't know how long he is going to save money. next you just add 3 as a checkpoint
Answer:
Y=4x+3
Step-by-step explanation:
4x represents the number of days he's added 4 and the 3 represents what he started off with.
Six students earned a perfect score on a history quiz. Only 5% of the entire grade earned a perfect score. How many students are in the grade?
Answers
Answer:
120
Step-by-step explanation:
If 6 = 5%, then 6 = 1/20 of the total grade. 6×20= 120
To evaluate whether customers enjoy the barista’s new smoothie, a restaurant manager surveys every other customer who orders the new smoothie. The manager determines that customers enjoy the new smoothie. Select all the statements that are true about the sampling method.
Answers
The sampling method used by the restaurant manager allows for efficient data collection and a representative sample, it may introduce bias and lacks randomization.
Based on the information provided, we can identify the following statements that are true about the sampling method used by the restaurant manager to evaluate customer satisfaction with the new smoothie:
1. The manager uses systematic sampling: The manager surveys every other customer who orders the new smoothie. This systematic approach involves selecting every second customer, providing a consistent and organized sampling method.
2. The sample is representative: By surveying every other customer who orders the new smoothie, the manager ensures that the sample includes a variety of customers, reflecting the customer population as a whole.
3. The sample size may be smaller than the total customer base: Since the manager surveys every other customer, the sample size may be smaller compared to surveying every customer. This allows for efficient data collection and analysis.
4.The sampling method may introduce bias: The manager may inadvertently introduce bias by only surveying every other customer. Customers who are skipped in the survey may have different preferences or opinions, leading to a potential bias in the results.
5. The sampling method lacks randomization: Randomization is not employed in this sampling method, as the manager systematically selects customers. This could potentially introduce bias or exclude certain types of customers from the sample.
for more such questions on sampling method
https://brainly.com/question/13219833
#SPJ8
A consumer interest group is comparing two brands of vitamin C. One group advertises that its tablets contain 500 mg of vitamin C. The other advertises that its tablets contain 250 mg of vitamin C. Tablets for each group were selected randomly. The table below shows the results.Vitamin C Content (mg) Brand A (500 mg) x = 250s = 500Brand B (250 mg) x = 500s = 10a) Calculate the coefficient of variation (CV) for Brand A (1point) b) Calculate the coefficient of variation (CV) for Brand B (1 point) c) Which brand more consistently produces tablets as advertised? (2 points) d) Explain your answer to c) above. (1 point)
Answers
a) The coefficient of variation (CV) for Brand A, is equals to the 2.8%.
b) The coefficient of variation (CV) for Brand B, is equals to the 2.0%.
c) Brand B, is more consistently produces tablets as advertised.
We have comparing data of consumer groups of vitamin C tablets of two brands. Tablets for each group were selected randomly. Data from above table, For brand A :
Tablets contains the quantity of vitamin C = 500 mg
Sample mean = 250
Standard deviation = 7
For brand B :
Tablets contains the quantity of vitamin C = 250 mg
Sample mean = 500
Standard deviations = 10
Cofficient of variation, CV is statistical parameter and it is the ratio of the standard deviation to the mean. Formula is, Coefficient of Variation (CV)
= (Standard Deviation/Mean) × 100.
a) To calculate the coefficient of variation (CV) for Brand A = (7/250 )×100
= 2.8%
b) To calculate the coefficient of variation (CV) for Brand B = (10/500 )×100
= 2.0%
c) As we see, Cofficient of variation of advertising for brand B is less than brand A. So, Brand B more consistently produces tablets as advertised.
Hence, required brand is brand B.
To learn more about Cofficient of variation, refer:
https://brainly.com/question/19616808
#SPJ4
Complete question:
consumer interest group is comparing two brands of vitamin C. One group advertises that its tablets contain 500 mg of vitamin C. The other advertises that its tablets contain 250 mg of vitamin C. Tablets for each group were selected randomly. The table above shows the results.Vitamin C Content (mg) Brand A (500 mg) x = 250s = 500Brand B (250 mg) x = 500s = 10
a) Calculate the coefficient of variation (CV) for Brand A (1point)
b) Calculate the coefficient of variation (CV) for Brand B (1 point)
c) Which brand more consistently produces tablets as advertised? (2 points) d) Explain your answer to c) above. (1 point)

By selling a stool for Rs. 67.50, a carpenter loses 10 %. How much percent would he gain by selling it for Rs 82.50?
Answers
Answer:
Rs. 7.50
or a gain of 10%
Step-by-step explanation:
Let x be the price of the stool
10% = 10/100 = 0.10
Loss = 0.1x
Selling price at 10% loss = x - 0.1x = 0.x
We are given this sale price is 67.50
So
0.9x = 67.50
x = 67.50/0.9 = 75
If he sells it at 82.50, the profit would be 82.50 - 75 = 7.5
This would represent a gain of 7.5/75 x 100 percent
= 10%
Answer:
The carpenter would gain 10% profit.
Step-by-step explanation:
67.5 is 90% of 75.
82.50 is 110% of 75.
"take a number x, double it and then take that result away from 10"
Write as an expression
Answers
Word Problem:
Take a number, x, double it and then take that result away from 10.
Expression:
\(10-(2x)\)
What is the graph of this function

Answers
A statement, rule, or regulation that establishes the relationship between an independent variable and a dependent variable is known as a function.
A network can be represented mathematically as a graph, which explains the connection between lines and points. A graph consists of some points with connecting lines.
Consider the function,
\(f(x)=\frac{||x||+2}{2}\) and 0 ≤ x ≤ 6
To graph the function we will find the points on the graph for different values of x.
When x = 0,
\(f(x)=\frac{||x||+2}{2}\)
\(f(x)=\frac{||0||+2}{2}=1\)
When x = 1,
\(f(x)=\frac{||x||+2}{2}\)
\(f(1)=\frac{||1||+2}{2}\\ f(1)=\frac{3}{2}\)
When x = 2,
\(f(x)=\frac{||x||+2}{2}\)
\(f(2)=\frac{||2||+2}{2}\)
\(f(2)=2\)
When x = 3,
\(f(x)=\frac{||x||+2}{2}\)
\(f(3)=\frac{||3||+2}{2}\)
\(f(3)=\frac{5}{2}\)
When x = 4,
\(f(x)=\frac{||x||+2}{2}\)
\(f(4)=\frac{||4||+2}{2}\\ f(4)=3\)
When x = 5,
\(f(x)=\frac{||x||+2}{2}\)
\(f(5)=\frac{||5||+2}{2}\)
\(f(5)=\frac{7}{2}\)
When x = 6,
\(f(x)=\frac{||x||+2}{2}\)
\(f(6)=\frac{||6||+2}{2} \\f(6)=4\)
Therefore, the points on the graph of the function \(f(x)=\frac{||x||+2}{2}\) are ( 0, 1 ), ( 1, ( 3/2 ) ), ( 2, 2 ), ( 2, ( 5/2 ) ), ( 4, 3 ), ( 5, ( 7/2 ) ), and ( 6, 4).
Hence, the graph of the function is:
Learn more about function here:
https://brainly.com/question/11624077
#SPJ9

Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
4(a + 2) + 2 = 4 - 2(-2a - 3)
Answers
Answer:
0=0
Step-by-step explanation:
4(a + 2) + 2 = 4 - 2(-2a - 3)
4a + 8 + 2 = 4 + 4a + 6
4a + 10 = 10 + 4a
0 = 0
Ubicar las siguientes fracciones en la recta numérica: 3/9
Answers
The most appropriate choice for Number line will be given by -
The number line has been shown in the figure attached.
What is a number line?
A visual representation of the real numbers can be shown on a diagrammatic representation of graduated straight lines. The visual representation of the real numbers is known as the number line. Number line can be used for addition or subtraction of two numbers.
Here,
The number line has been attached
\(\frac{3}{9}\) lies between 0 and 1
So the space between 0 and 1 is divided into 9 equal parts as the denominator of the given fraction is 9
Now the third small line is the required value i.e \(\frac{3}{9}\) as 3 is in the numerator of the given fraction
To learn more about number line, refer to the link:
https://brainly.com/question/24644930
#SPJ9

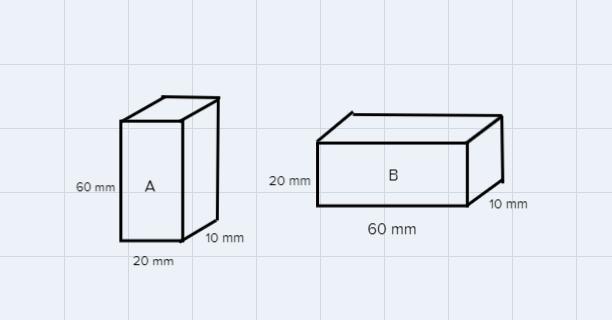
A student has an L-shaped eraser as shown below with the dimensions given. If the factory that produces this eraser sells them in packs of 20, how many cubic millimeters of eraser material do they need to create each pack of eraser?
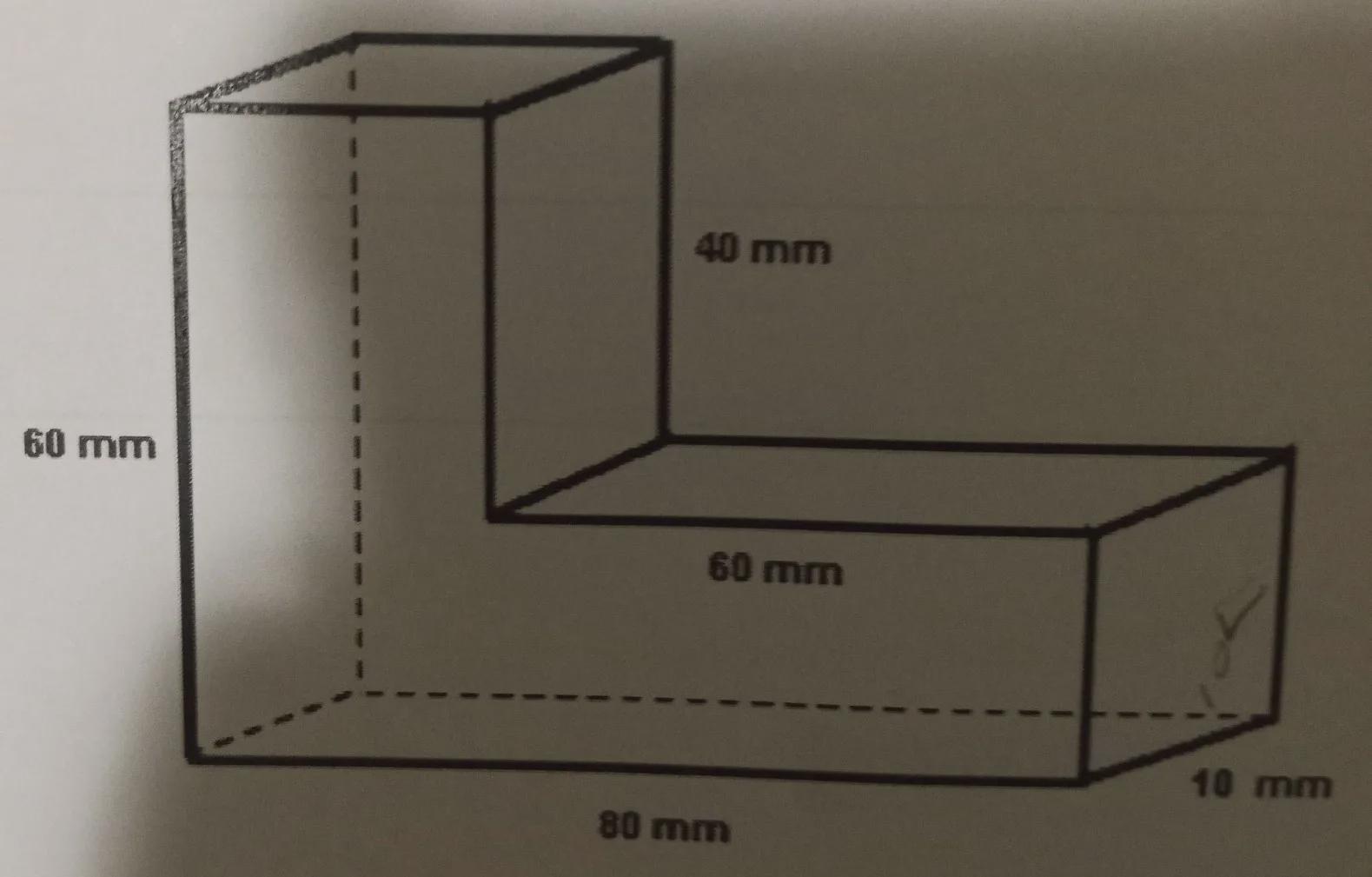
Answers
ANSWER
\(480,000\operatorname{mm}^3\)EXPLANATION
We want to find the volume of 20 L-shaped erasers.
First, we have to find the volume of one eraser. To do this, we have to partition the eraser into two rectangular prisms:
To find the volume of the prism, apply the formula:
\(V=L\cdot W\cdot H\)where L = length; W = width; H = height
Therefore, for A, we have:
\(\begin{gathered} V_A=60\cdot20\cdot10 \\ V_A=12,000\operatorname{mm}^3 \end{gathered}\)And for B, we have:
\(\begin{gathered} V_B=60\cdot20\cdot10 \\ V_B=12,000\operatorname{mm}^3 \end{gathered}\)The volume of the shape is the sum of the volumes of the partitions. Hence, the volume of the shape is:
\(\begin{gathered} V=V_A+V_B_{} \\ V=12,000+12,000 \\ V=24,000\operatorname{mm}^3 \end{gathered}\)Hence, a pack of 20 will have a volume of:
\(\begin{gathered} V=20\cdot24,000 \\ V=480,000\operatorname{mm}^3 \end{gathered}\)That is the amount of material needed to create each pack of erasers.
some PLEASE help I need it done in 18 minutes
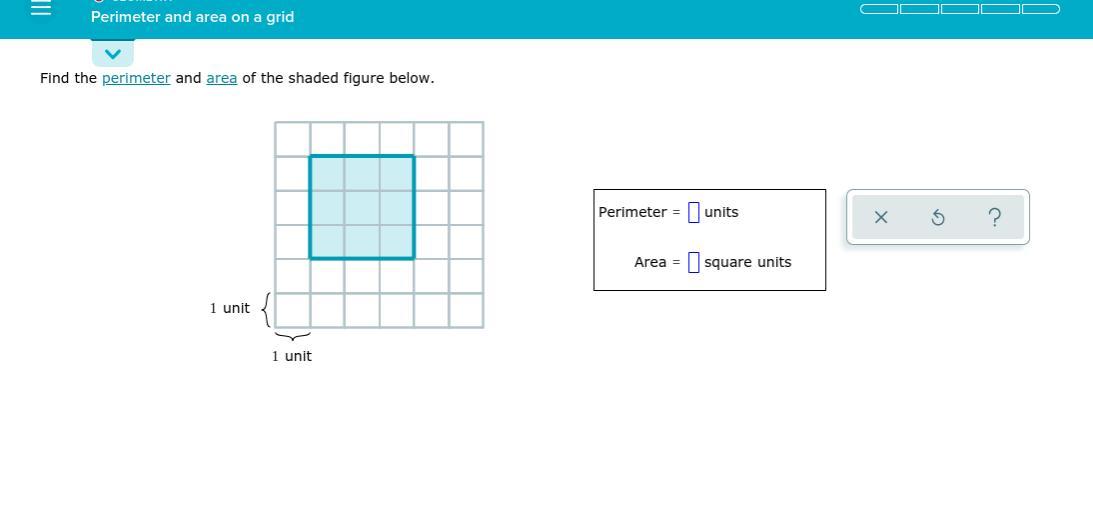
Answers
Answer:
area: 9
perimeter: 12
Step-by-step explanation:
Answer:
i gotchu
u=4a (equation for perimiter)
u=12
perimeter is 12
a=a2 (equation for area)
a=9
area is 9
:)
Answer the dammm question and I will give you brainlist if you do the whole thing pleaseeeeee more then 1 person at least help me nobody will

Answers
Answer:
the coordinate is (4,5)
he said it was negative when it is actually positive
Step-by-step explanation:
i think
Hope your day is good
So the correct coordinates for Q (4,5)
He got his answer if the triangle was at the 2nd one down
So the correct Q coordinates is (4,5) not one negative and a positive x and y
Hope this helps you out
*smiles*
Timothy bought a house for $360,000. He paid 20% down, and agreed to pay $1,375.69 per month for 30 years. His payment of $1,375.69 does not include property tax and insurance. How much interest will Timothy pay in 30 years?
Answers
It's difficult to determine exactly how much interest Timothy will pay over 30 years without more information about the terms of his mortgage. However, we can use the following formula to calculate his monthly mortgage payment, which includes both the principal and the interest:
Monthly payment = P * (r/12) / (1 - (1 + r/12)^(-n))
Where:
P is the principal amount (the total cost of the house minus the down payment)
r is the monthly interest rate (we need to convert the annual interest rate to a monthly rate by dividing it by 12)
n is the number of payments (in this case, the number of months over which Timothy will pay off the mortgage, which is 30 years * 12 months/year = 360 months)
We can plug in the given values to find Timothy's monthly payment:
Monthly payment = $360,000 * (0.04/12) / (1 - (1 + 0.04/12)^(-360)) = $1,375.69
To find the total amount of interest Timothy will pay over 30 years, we would need to know the interest rate on his mortgage and the length of the loan in months. With this information, we could calculate the total amount of interest Timothy will pay by multiplying his monthly payment by the number of payments he makes (360 payments in this case) and subtracting the principal amount ($360,000).
What is the additive inverse of the number given below?
6
Answers
Answer:
-6 is the answer for instance 6=-6 or +(-6)
what is 4/90 reduced
Answers
Answer:
2/45
Step-by-step explanation:
divide both sides by 2
4/2=2
90/2=45
2/45
4
90
is
2
45 ............