common demominator of 1/3 and 3/4
Answers
Answer:12 is a common denominator!
Step-by-step explanation:
Related Questions
Determine the equation of a straight line passing through the point (1, 0) and (2, -3)
Answers
Answer:
y = -3x - 3
Step-by-step explanation:
By equation of a straight line, this could mean:
Slope intercept form: \(y=mx+b\)
Point slope form: \(y-y1=m(x-x1)\)
Because we do not have the y intercept, it would be much easier to write it in point slope form where y1 and x1 are points and m is the slope.
First, we need to find the slope. We can do this by using the slope formula \(\frac{y2-y1}{x2-x1}\) where y2, y1, x2, and x1 are points.
\(\frac{-3-0}{2-1}\)
Evaluate
\(\frac{-3}{1}=-3\)
Now that we have the slope, lets use the ordered pair (1,0) and write the equation of the line in point slope form.
\(y-0=-3(x-1)\)
Simplify
\(y=-3x-3\)
Would you look at that, we get the equation of the line in slope intercept form!
A triangle has squares on its three sides as shown below. What is the value of x? 3 cm U x cm 4 cm 3 centimeters 4 centimeters 5 centimeters 07 centimeters A triangle has squares on its three sides as shown below . What is the value of x ? 3 cm U x cm 4 cm 3 centimeters 4 centimeters 5 centimeters 07 centimeters
Answers
The value of x is 10 centimeters
How to solve for x?The complete question is in the image
The value of x is calculated using the following Pythagoras theorem
x^2 = 6^2 + 8^2
Evaluate the sum of exponents
x^2 = 100
Take the square roots
x = 10
Hence, the value of x is 10 centimeters
Read more about right triangles at:
https://brainly.com/question/2437195
#SPJ1

Help me please!!!!!!!!!!!!

Answers
Answer:
1. 2,772
2.1,071
3.4,641
4. 36,610
5. 4,096
6. 36,270
7. 2,403
8. 3,320
∎ = 28 ÷ 4 try it maybee?
Answers
Answer:
28÷4=7
Step-by-step explanation:
Answer:
7
Step-by-step explanation:
Hello there! Grace is here to help you! :)
28:4=7
Hope it helps!
______
Additional Comment
If you found my answer helpful, please mark Brainliest! :)
Witch describes the slope of this line?
undefined
zero slope
negative slope
positive slope

Answers
Answer:
Undefined
Step-by-step explanation:
Will give BRAINLIEST

Answers
Answer:
Y=4x
Step-by-step explanation:
Answer:
1/4 per hour
Step-by-step explanation:
1 bracelet in 4 hours
1 divided by 4 = 1/4
1/4 bracelets per hour
Find the value of x and y in simplified radical form.

Answers
x and y have the values 7 and 7√2, respectively.
The sides of a right triangle with 45-degree acute angles have a unique ratio of 1:1:2.
We can use this information to determine the values of x and y because the base is specified as being 7.
Let's give the perpendicular side the value of x, and the hypotenuse the value of y.
The perpendicular side (x) and the base (7) have the same length because the acute angles are both 45 degrees.
Consequently, x = 7.
We can determine that x:y:2x using the ratio of 1:1:2.
When we enter the value of x, we may calculate y:
7:y:√2(7)
Simplifying even more
7:y:7√2
Given that the hypotenuse (y) equals 72, we can write:
y = 7√2
Thus, x and y have the values 7 and 7√2, respectively.
Learn more about right triangle click;
https://brainly.com/question/30966657
#SPJ1
A store can buy 8 cartons of milk for $24 or 7 cartons of milk for $28.
How much less does each carton of milk cost if the store buys 8 cartons instead of 7 cartons?
A.
$1 less
B.
$2 less
C.
$3 less
D.
$4 less
Answers
Answer:
A. $1 less
Step-by-step explanation:
24 divided by 8 (unit rate) = $3
28 divided by 7 = $4
4-3=1
What’s the square root of √125
Answers
Answer: \(5\sqrt 5\)
Step-by-step explanation:
Sol \(\sqrt 125\) = \(\sqrt{25.5}\)
= \(\sqrt{25}\) x \(\sqrt{5}\)
\(5 \sqrt{5}\)
simplify 2x²y²÷m³×m²÷2xy
Answers
Triangle HIJ is similar to triangle KLM find the measure of side KL around your answer to the nearest tenth if necessary
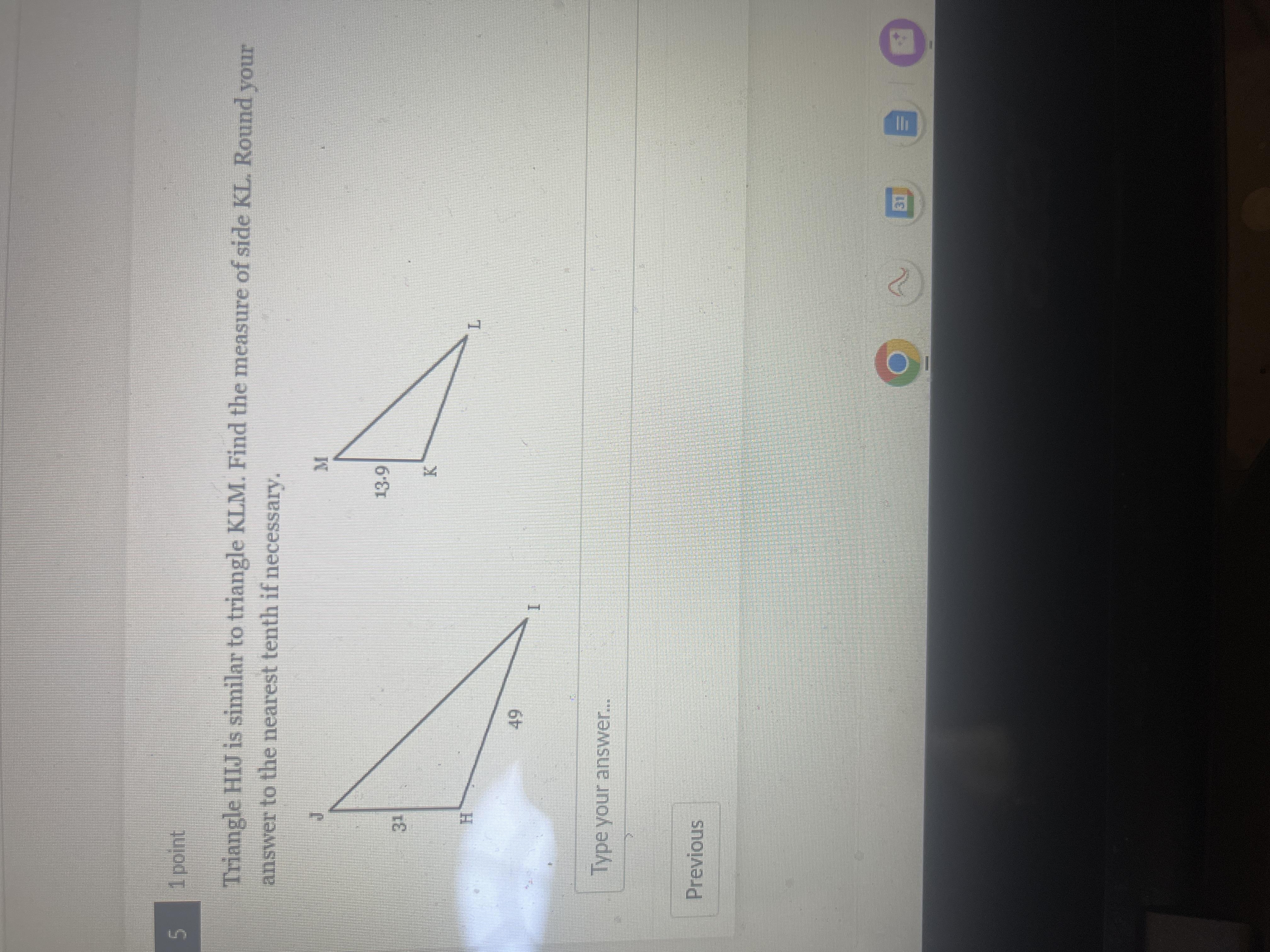
Answers
The measure of side KL from triangle KLM is 22 units.
What are similar triangles?Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Either of these conditions will prove two triangles are similar.
Given that, triangle HIJ is similar to triangle KLM.
From the similar triangles,
JH/MK =HI/KL
31/13.9 =49/KL
31KL=49×13.9
31KL=681.1
KL=681.1/31
KL=21.97
KL≈22
Therefore, the measure of side KL is 22 units.
To learn more about the similar triangles visit:
https://brainly.com/question/25882965.
#SPJ1
Can the following quadrilateral be proven to be a parallelogram based on the given information? Explain.
(picture shown below)
A.) No. It cannot be proven because at least two of the adjacent angles are not congruent to each other
B.) Yes. It can be proven because both pairs of opposite sides are congruent.
C.) No. It cannot be proven because it does not have an angle that is supplementary to both of its consecutive angles.
D.) Yes. It can be proven because both pairs of opposite angles are congruent.

Answers
Answer:
Step-by-step explanation:
The answer is, no!
Step-by-step explanation:
The reason to that answer is that some other shapes are also, having the same properties as shown. An example for that property would also mean a rectangle and not always a parallelogram.
So, here is the given information on what we need to classify a shape as a parallelogram:-
1) Parallel Sides
2)Opposite Sides are equal.
3) Adjacent sides are not equal.
4) Opposite angles are equal.
5)Adjacent angles are not equal.
Based on this, we can classify a shape as a parallelogram.
Hope, this answer helps!
HELP PLEASE HELP PLEASE

Answers
Answer:
D 1/4
Step-by-step explanation:
Your question is a problem in reading comprehension. It tells you its own answer.
x is always 1/4

Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answers
Answer:
The answer is 16pi or 50.3cm² to 1 d.p
Step-by-step explanation:
The non shaded=area of shaded
d=8
r=d/2=4
A=pir³
A=p1×4²
A=pi×16
A=16picm² or 50.3cm² to 1d.p
Answer:
3.45 cm (3 s.f.)
Step-by-step explanation:
We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.
To find the radius of a regular polygon given its side length, we can use this formula:
\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):
\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)
The formulas for the area of a regular polygon and the area of a circle given their radii are:
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Therefore, the area of the regular pentagon is:
\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)
The area of the circumcircle is:
\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.
The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.
Given the shaded area is equal to the unshaded area:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)
\(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

The variables x and y are connected by the equation y=(x-3)(x - 5)(x+2).Some corresponding values of x and y are shown in the table below. X -2 0 1 y 0 30 24 (i) Calculate the value of k -1 24 2 12 3 0 4 -6 5 0 (0) 6 k [1] avis
Answers
The value of k is given as follows:
k = 24.
How to find the numeric value of a function or of an expression?To find the numeric value of a function or of an expression, we replace each instance of the variable in the function or in the expression by the value at which we want to find the numeric value.
From the table, we have that when x = 6, y = k, hence the value of k is found replacing each of the three instances of x by 6, as follows:
k = (6 - 3)(6 - 5)(6 + 2)
k = 3 x 1 x 8
k = 24.
Learn more about the numeric values of a function at brainly.com/question/28367050
#SPJ1
Solve this equation by transposing 4+5(m-1)=34
Answers
Answer:
Solving the equation \(4+5(m-1)=34\\\) we get m=7
Step-by-step explanation:
We need to solve the equation \(4+5(m-1)=34\\\) and find value of m
Solving using transpose method which states that if one term is added one one side, it gets subtracted on other side of equality
\(4+5(m-1)=34\\Multiply \ 5 \ with \ terms \ inside \ the \ brackets\\4+5m-5=34\\5m+4-5=34\\5m-1=34\\Adding \ 1 \ on \ both \ sides\\5m-1+1=34+1\\5m=35\\Divide \ by \ 5\\\frac{5m}{5} =\frac{35}{5}\\m=7\)
So, solving the equation \(4+5(m-1)=34\\\) we get m=7
There is an urn containing 9 balls, which can be either green or red. Let X be the number of red balls in the urn, which is unknown. As a prior, assume that all possible values of X from 0 to 9 are equally likely. (a) One ball is drawn at random from the urn, and it is red. Compute the Bayes box to give the posterior probability distribution of X. Calculate the posterior mean of X. (b) Suppose that a second ball is drawn from the urn, without replacing the first, and it is green. Use the posterior distribution of X from part a) as the prior distribution for X and compute the Bayes box and to give the posterior probability distribution of X. Calculate the mean of X.
Answers
(a) One ball is drawn at random from the urn and it is red, so the posterior distribution of X can be found using Bayes' theorem:
P(X = x | red) = P(red | X = x) * P(X = x) / P(red)
where P(X = x) is the prior probability of X being x, P(red | X = x) is the probability of getting a red ball given that X is x, and P(red) is the total probability of getting a red ball.
Since all possible values of X from 0 to 9 are equally likely, the prior probability of X being x is P(X = x) = 1/10 for x = 0, 1, 2, ..., 9.
The probability of getting a red ball given that X is x can be calculated using the hypergeometric distribution:
P(red | X = x) = (x choose 1) * (9-x choose 8-x) / (9 choose 1)
where (x choose k) is the number of combinations of x items taken k at a time.
The total probability of getting a red ball is:
P(red) = sum(P(red | X = x) * P(X = x)) for x = 0, 1, 2, ..., 9
Using these formulas, we can find the posterior distribution of X and the mean of X:
Posterior distribution of X:
P(X = x | red) = P(red | X = x) * P(X = x) / P(red)
Mean of X:
E(X | red) = sum(x * P(X = x | red)) for x = 0, 1, 2, ..., 9
(b) Now suppose that a second ball is drawn from the urn, without replacing the first, and it is green, so the posterior distribution of X can be found using Bayes' theorem again:
P(X = x | red, green) = P(green | X = x) * P(X = x | red) / P(green)
where P(X = x | red) is the posterior distribution of X from part (a), P(green | X = x) is the probability of getting a green ball given that X is x, and P(green) is the total probability of getting a green ball.
The probability of getting a green ball given that X is x can be calculated using the hypergeometric distribution:
P(green | X = x) = (9-x choose 1) * (x choose 8-x) / (9 choose 1)
The total probability of getting a green ball is:
P(green) = sum(P(green | X = x) * P(X = x | red)) for x = 0, 1, 2, ..., 9
Using these formulas, we can find the posterior distribution of X and the mean of X:
Posterior distribution of X:
P(X = x | red, green) = P(green | X = x) * P(X = x | red) / P(green)
Mean of X:
E(X | red, green) = sum(x * P(X = x | red, green)) for x = 0, 1, 2, ..., 9
To know more about Bayes' theorem
https://brainly.com/question/17010130
#SPJ4
A soda factory makes 9 flavours of soda. Each case of soda has 7 cans of each flavour. How many cans of soda does the factory put in 7 cases?
Answers
The factory will put 441 cans of soda in 7 cases.
If each case of soda contains 7 cans of each flavor, and the factory is putting 7 cases, we can calculate the total number of cans by multiplying the number of flavors, cans per flavor, and cases.
Given:
Number of flavors = 9
Cans per flavor = 7
Number of cases = 7
To calculate the total number of cans, we can multiply these values:
Total cans = Number of flavors × Cans per flavor × Number of cases
Total cans = 9 × 7 × 7
Total cans = 441
To arrive at this answer, we multiplied the number of flavors (9) by the number of cans per flavor (7) to get the number of cans per case (63). Then, we multiplied the cans per case (63) by the number of cases (7) to obtain the total number of cans (441).
Hence, the factory will put 441 cans of soda in 7 cases.
For more such questions on soda
https://brainly.com/question/29111121
#SPJ8
Container A has 300 liters of water, and is being filled at a rate of 6 liters per minute. Container B has 900 liters of water, and is being drained at 2 liters per minute. How many minutes, m, will it take for the two containers to have the same amount of water?
Answers
It will take 150 minutes for the two containers to have the same amount of water.
To find the number of minutes it will take for the two containers to have the same amount of water, we need to use the following formula:
m = |A - B| / (a - b)
where m is the number of minutes, A is the initial amount of water in Container A, B is the initial amount of water in Container B, a is the rate at which water is being added to Container A, and b is the rate at which water is being drained from Container B.
In this case, the initial amount of water in Container A is 300 liters, the initial amount of water in Container B is 900 liters, the rate at which water is being added to Container A is 6 liters per minute, and the rate at which water is being drained from Container B is 2 liters per minute. Substituting these values into the formula, we get:
m = |300 - 900| / (6 - 2)
m = |-600| / 4
m = 600 / 4
m = 150 minutes
Therefore, it will take 150 minutes for the two containers to have the same amount of water.
To learn more about numerical expression click here :
https://brainly.com/question/6037813
#SPJ1
5
An athlete covers three consecutive miles by walking the first mile, running the second mile
and cycling the third. He runs twice as fast as he walks, and he cycles one and a half times as
ast as he runs. He takes ten minutes longer than he would do if he cycled the three miles,
How long does he take by walking, running and cycling?
ter your math answer
Answers
Answer:
Total time taken by walking, running and cycling = 22 minutes.
Step-by-step explanation:
Let the speed of walking = x
As given,
The distance of walking = 1
Now,
As \(Time = \frac{Distance }{Speed}\)
⇒ Time traveled by walking = \(\frac{1}{x}\)
Now,
Given that - He runs twice as fast as he walks
⇒Speed of running = 2x
Also given distance traveled by running = 1
Time traveled by running = \(\frac{1}{2x}\)
Now,
Given that - he cycles one and a half times as fast as he runs.
⇒Speed of cycling = \(\frac{3}{2}\) (2x) = 3x
Also given distance traveled by cycling = 1
Time traveled by cycling = \(\frac{1}{3x}\)
Now,
Total time traveled = Time traveled by walking + running + cycling
= \(\frac{1}{x}\) + \(\frac{1}{2x}\) + \(\frac{1}{3x}\)
= \(\frac{6+3+2}{6x} = \frac{11}{6x}\)
If he cycled the three mile , then total time taken = \(\frac{1}{3x}\) + \(\frac{1}{3x}\) + \(\frac{1}{3x}\) = x
Given,
He takes ten minutes longer than he would do if he cycled the three miles
⇒x + 10 = \(\frac{11}{6} x\)
⇒\(x - \frac{11}{6} x = -10\)
⇒\(-\frac{5}{6}x = -10\)
⇒x = \(\frac{60}{5}\) = 12
⇒x = 12
∴ we get
Total time traveled by walking + running + cycling = \(\frac{11}{6} x = \frac{11}{6} (12) = 11 (2) = 22\) min
Select the correct answer. Rewrite the following expression.

Answers
The solution of the expression, \(x^{\frac{9}{7} }\) is \(\sqrt[7]{x^{9} }\).
How to solve an expression?An expression is a combination of numbers, variables, functions such as addition, subtraction, multiplication or division etc.
Therefore, let's rewrite the expression to it's equivalent expression.
An equivalent expression is an expression that has the same value or worth as another expression, but does not look the same.
Therefore, using indices rule
\(x^{\frac{9}{7} }\) = \(\sqrt[7]{x^{9} }\)
learn more on expression here: https://brainly.com/question/11133268
#SPJ1
The scatter plot shows the number of chin-ups and push-ups completed by a sample of fourth grade students.
What is the median number of chin-ups for all students?
Student Name
Label
Number of Chin-ups and Push-ups
10-
9
А
B
H
B
8
Jared
Tonya
Alex
Rishab
L
D
G
с
7-
F
D
K к
Gao
E
E
А
с
F
Riki
Anne
5-
4-
3
2-
G
Amira
H
12
/
Samuel
Lily
0
J
1
6
8
9
10
Abdu
K
2
Chin-ups
Mike
Answers
Answer:
9
Step-by-step explanation:
One did 10,one did 9, and 1 did 8 and 9 is the median number of those 3 numbers.
Answer:
Abdu, Tonya, Gao, Lily, Mike, Rishab
Step-by-step explanation:

very important! please answer!!

Answers
Answer:
I'm pretty sure the answer is 42. You just subtract 180 and 138 because the KD line would be 180.
Which mapping diagram is NOT a function?

Answers
Answer:
D is not a function--an x-value cannot correspond to more than one y-value.
The cost of the new Samsung galaxy is $499. The tax is 8.5%. What will the total cost of the phone be? Round your answer to the nearest penny
Answers
$499x8.5=58.70
Answer:
$541.41
Step-by-step explanation:
the tax is $42.41
so if you add that to $499 you get
499+42.41= 541.41
Write a system of equations in the standard form to solve for those quantities.
Answers
It should be noted that to write a system of equations in standard form, you need to express each equation in the form Ax + By = C, where A, B, and C are constants and x and y are variables. The steps are given below.
How to illustrate the stepsHere are the steps to follow:
Rewrite each equation in standard form by moving all the variables to one side and all the constants to the other side.
Make sure that the coefficients of x and y are integers and, if possible, that they have a greatest common factor of 1. If the coefficients have a common factor, divide both sides of the equation by that factor to simplify the equation.
Arrange the equations in standard form in a matrix form. You can write the matrix form by lining up the coefficients of x, y, and the constants in a matrix.
Finally, you can also represent the system of equations in standard form using variables and constants.
This is the standard form of a system of linear equations.
Note that an overview was given since your information is incomplete.
Learn more about equations on:
https://brainly.com/question/2972832
#SPJ1
Please help! Show work as welll pleaseeeee

Answers
Answer:
\( {x}^{2} + {8}^{2} = {y}^{2} ...(1) \\ {x}^{2} + {23}^{2} = {z}^{2} ...(2) \\ {y}^{2} + {z}^{2} = {(23 + 8)}^{2} \\ {y}^{2} + {z}^{2} = {(31)}^{2} ...(3) \)
You should be able to solve this simultaneously...to find x,y and z.
find the value of 8w+6 given that -7w+1=8
Answers
Answer: -2
Step-by-step explanation:
-7w + 1 = 8
Subtract 1 from both sides
-7w + = 7
Divide -7 from both sides
w = -1
then
8(-1) = -8
-8 + 6 = -2
There is a ratio of 9 kangaroos to 7 emus. If there are 49 emus, how many total animals are there
Answers
The total number of animals are 112 if the ratio of kangaroos to emus is 9:7 and the number of emus are 49.
What is meant by ratio?A ratio in mathematics displays the multiplicative relationship between two numbers. In a bowl of fruit, for instance, the proportion of oranges to lemons is eight to six if there are eight oranges and six lemons (that is, 8:6, which is equivalent to the ratio 4:3).
A ratio can have any number of numbers as its components, including counts of people or things, weights, lengths, and times, among other values.
Given,
The ratio of kangaroos to emus is 9:7
And also given that the number of emus=49
Since, the ratio is 9:7
The number of kangaroos=63
63:49
9:7
Total number of animals=63+49
=112
Therefore, the total number of animals are 112 if the ratio of kangaroos to emus is 9:7 and the number of emus are 49.
To know more about ratio, visit:
https://brainly.com/question/13419413
#SPJ1
What are the end behaviors of f(x) = (1/3)^x – 2 ?
Answers
Answer:
\(\lim_{x\to -\infty} f(x)=\infty,\\\lim_{x\to \infty} f(x)=2,\)
Step-by-step explanation:
The end behaviors of a function simply denote where the function is headed at x approaches negative and positive infinity. In \(f(x)=\left(\frac{1}{3}\right)^x+2\), as \(x\) gets approaches \(-\infty\), the function will approach \(y=\infty\). As \(x\) approaches \(\infty\), the function will approach \(y=2\).
We can write this in the following format to denote these end behaviors:
\(\lim_{x\to -\infty} f(x)=\infty,\\\lim_{x\to \infty} f(x)=2,\)