Compare the two leagues and predict which league would be more likely to win a game.

Answers
Answer:
(This is the Sample Answer)
The team from the second league would be more likely to win because teams in that league have more consistent, and mostly greater, numbers of home runs and winning games. Data for teams in the second league also do not show any outliers.
Answer:
sample answer
Step-by-step explanation:
The team from the second league would be more likely to win because teams in that league have more consistent, and mostly greater, numbers of home runs and winning games. Data for teams in the second league also do not show any outliers.
Related Questions
A manufacturer receives a shipment of 100 parts from a vendor. The shipment will be unacceptable if more than five of the parts are defective. The manufacturer is going to randomly select K parts from the shipment for inspection, and the shipment will be accepted if no defective parts are found in the sample. How large does K have to be to ensure that the probability that the manufacturer accepts an unacceptable shipment is less than 0.1? Hint: We recommend using R to plug in different values of K.
A. 42
B. 22
C. 32
D. 12
Answers
Answer:
C. 32
Step-by-step explanation:
The shipment for 100 parts is received by a manufacturer. Shipment will be rejected if more than 5 parts are defective. The manufacturer selects a sample and based on that selected sample he accepts or rejects the whole shipment. The minimum size of the sample should be 32 based on the probability of less than 0.1 and then decision should be made whether to accept or reject the shipment. If no defective part is found in the sample, shipment should be accepted.
What is the name of the segment inside the large triangle?
1. Perpendicular bisector
2.Midsegment
3.Angle Bisector
4.Median

Answers
The name of the segment inside the large triangle is called the: 3. angle bisector.
What is an Angle Bisector?The word "bisect" means to divide into two equal halves. Therefore, an angle bisector can be defined as a line segment that divides the an angle in a triangle into two parts that are of the same angle measure.
The image shows a triangle which has a segment that divides a vertex angle into equal parts. Thus, the segment can be named as an angle bisector.
A perpendicular bisector divides a segment into two equal halves at right angle, while a midsegment joins the middle points of two sides of a triangle. The median also, is a segment that joins a vertex of a triangle to the midpoint of the side that is opposite the angle.
Therefore, we can state that the name of the segment is: 3. angle bisector.
Learn more about the angle bisector on:
https://brainly.com/question/24334771
#SPJ1
from 8 names on a ballot, a committee of 5 will be elected to attend a political national convention. how many different committees are possible?
Answers
There are a total of 56 possible committees.
Given data,
From 8 names on a ballot, a committee of 5 will be elected to attend a political national convention.
To know how many different committees are possible;
From the given data,
By using the combinations we get,
⇒ ⁸C₅
⇒ ⁸C₅ = \(\frac{8!}{5!*(8-5)!}\)
= 56
Therefore, a total of 56 different committees is possible.
To learn more about combinations click here:
brainly.com/question/28042664
#SPJ4
How do I write an equation in slope-intercept form for the line with slope 2/3 & y-intercept -3
Answers
Answer:
Step-by-step explanation:
ok equation are like fraction but let me put it like this lets say x+y=7;x+2y=11 thats how you do eqution done.
How many times does 45 go into 704
Answers
Answer:
15.64
Step-by-step explanation:
Answer:
15.64 times
Step-by-step explanation:
704/45= 15.64
the mean number of pets owned by the population of students at a large high school is 3.2 pets per student with a standard deviation of 1.7 pets. a random sample of 16 students will be selected and the mean number of pets for the sample will be calculated.
Answers
What is the general solution to the differential equation dy over dx equals x times y plus 2 times x
Answers
The general solution to the given differential equation, \(\frac{dy}{dx}\) = x × y + 2 × x, can be found by separating the variables and integrating.
Step 1:
Rearrange the equation to separate the variables:
dy = (x × y + 2 × x) dx
Step 2:
Divide both sides by (y + 2x):
\(\frac{dy}{y + 2x}\) = x dx
Step 3:
Integrate both sides of the equation:
∫(\(\frac{1}{y + 2x}\))) dy = ∫x dx
Step 4:
Solve the integrals separately:
ln|y + 2x| = (\(\frac{1}{2}\)) × x² + C1
Step 5:
Remove the natural logarithm by taking the exponential of both sides:
|y + 2x| =\(e^{\frac{1}{2} }\) × x² + C1)
Step 6:
Consider two cases: positive and negative values of (y + 2x).
Case 1:
(y + 2x) > 0
y + 2x
= \(e^{\frac{1}{2} }\) × x² + C1)
Case 2:
(y + 2x) < 0
-(y + 2x)
= \(e^{\frac{1}{2}}\) × x² + C1
Step 7:
Simplify the equations:
y = -2x + \(e^{\frac{1}{2} }\) × x² + C1) (for (y + 2x) > 0)
y = -2x - \(e^{\frac{1}{2} }\) × x² + C1) (for (y + 2x) < 0)
These are the general solutions to the given differential equation.
They describe all possible solutions in terms of an arbitrary constant, C1.
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
The general solution to the given differential equation is \(y = Ke^{x^2}\), where K is a non-zero constant. This solution represents a family of curves that satisfy the given differential equation.
The general solution to the differential equation \(\frac{dy}{dx} = xy + 2x\) can be found using the method of separable variables. Here's how you can solve it:
1. Rewrite the equation:
\(\frac{dy}{dx} = xy + 2x\)
2. Separate the variables by moving all terms involving y to one side and terms involving x to the other side:
\(\frac{dy}{y} = 2xdx.\)
3. Integrate both sides separately:
\(\int(\frac{dy}{y}) = \int2xdx.\)
4. Integrate the left side by applying the natural logarithm property:
\(ln|y| = x^2 + C_1\)
where:
\(C_1\) is the constant of integration.
5. Integrate the right side:
\(\int 2xdx = x^2 + C_2\)
where:
\(C_2\) is another constant of integration.
6. Combine the integration results:
\(ln|y| = x^2 + C_1 + C_2\)
7. Rewrite the equation using properties of logarithms:
\(ln|y| = x^2 + C\)
8. Solve for y by taking the exponential of both sides:
\(|y| = e^{(x^2+C)}\)
9. Remove the absolute value by considering two cases:
\(y = \pm e^{(x^2+C)}\)
10. Simplify the expression:
\(y = Ke^{x^2}\)
where K is a non-zero constant.
In conclusion, the general solution to the given differential equation is \(y = Ke^{x^2}\), where K is a non-zero constant. This solution represents a family of curves that satisfy the given differential equation.
Learn more about differential equation from the given link:
https://brainly.com/question/1164377
#SPJ11
Encuentre el mayor factor común de 12 y 16
Answers
The greatest common factor (MFC) of 12 and 16 is 4. By both the prime factorization method and the common divisors method.
To find the greatest common factor (MFC) of 12 and 16, we can use different methods, such as the prime factorization method or the common divisors method.
Decomposition into prime factors:
First, we break the numbers 12 and 16 into prime factors:
12 = 2*2*3
16 = 2*2*2*2
Then, we look for the common factors in both decompositions:
Common factors: 2 * 2 = 4
Therefore, the MFC of 12 and 16 is 4.
Common Divisors Method:
Another method to find the MFC of 12 and 16 is to identify the common divisors and select the largest one.
Divisors of 12: 1, 2, 3, 4, 6, 12
Divisors of 16: 1, 2, 4, 8, 16
We note that the common divisors are 1, 2, and 4. The largest of these is 4.
Therefore, the MFC of 12 and 16 is 4.
In summary, the greatest common factor (MFC) of 12 and 16 is 4. By both the prime factorization method and the common divisors method, we find that the number 4 is the greatest factor that both numbers have in common.
for more such question on factorization visit
https://brainly.com/question/25829061
#SPJ8
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
Suppose on average, a high school loses about 5 students each year, because they leave to attend a charter school. Which best describes this relationship?
A. A linear function because the students are decreasing by 5 each year.
B. An exponential function because the students are decreasing by 5 each year.
C. An exponential function because there is a 5% decay.
D. A linear function because there is a 5% decay.
Answers
1. If f(x) = (3x-2)/(2x+3), then f'(x) =
Answers
Answer:
\(f'(x)= \frac{13}{(2x+3)^2}\\\)
Step-by-step explanation:
\(f(x)= \frac{3x-2}{2x+3} \\\)
\(f'(x)=\frac{dy}{dx} = \frac{d}{dx}(\frac{3x-2}{2x+3})\\ f'(x)= \frac{(2x+3)\frac{d}{dx}(3x-2)-(3x-2)\frac{d}{dx}(2x+3) }{(2x+3)^{2} } \\f'(x)= \frac{(2x+3)(3)-(3x-2)(2)}{(2x+3)^{2} } \\\)
\(f'(x)= \frac{6x+9-6x+4}{(2x+3)^{2} }\\ f'(x)= \frac{13}{(2x+3)^2}\\\)
What is the midpoint of points (3.9) and (1.-7)?
Answers
Answer:
Answer is (2,1)
Step-by-step explanation:
The Midpoint formula is simply (x2+x1)/2, (y2+y1/2)
Just gotta plug in the points!
Hope this helps!
sketch the signal
1)u(t-5)-u(t-7)
2)u(t-5) +u(t-7)
3) (t-4)[u(t-2)-u(t-4)]
Answers
a) A pulse of width 2 units, starting at t=5 and ending at t=7.
b) A sum of two pulses of width 1 unit each, one starting at t=5 and the other starting at t=7.
c) A ramp starting at t=2 and ending at t=4.
Part 2
a) A rectangular pulse of height 1, starting at t=5 and ending at t=7.
b) Two rectangular pulses of height 1, one starting at t=5 and the other starting at t=7, with a gap of 2 units between them.
c) A straight line starting at (2,0) and ending at (4,2).
In part 1, we are given three signals and asked to identify their characteristics. The first signal is a pulse of width 2 units, which means it has a duration of 2 units and starts at t=5 and ends at t=7. The second signal is a sum of two pulses of width 1 unit each, which means it has two parts, each with a duration of 1 unit, and one starts at t=5 while the other starts at t=7. The third signal is a ramp starting at t=2 and ending at t=4, which means its amplitude increases linearly from 0 to 1 over a duration of 2 units.
In part 2, we are asked to sketch the signals. The first signal can be sketched as a rectangular pulse of height 1, starting at t=5 and ending at t=7. The second signal can be sketched as two rectangular pulses of height 1, one starting at t=5 and the other starting at t=7, with a gap of 2 units between them. The third signal can be sketched as a straight line starting at (2,0) and ending at (4,2), which means its amplitude increases linearly from 0 to 2 over a duration of 2 units. It is important to note that the height or amplitude of the signals in part 2 corresponds to the value of the signal in part 1 at that particular time.
Learn more about corresponds
brainly.com/question/12454508
#SPJ11
evaluate the inequality
6x-2y+8 when x=3 and y=2
show your work
Answers
Answer:
22
Step-by-step explanation:
6(3)-2(2)+8
18-4+8
14+8
22
Answer:
22
Step-by-step explanation:
6x-2y+8
(6 • 3) - (2 • 2) + 8
18 - 4 + 8
22
(i think)
The diagram shows the shape of a plot of land that Maria will use for her garden. Quadrilateral F G H J is shown. Sides G H and F J are parallel. The length of F G is 30 feet, the length of G H is 24 feet, and the length of H J is 24 feet. Angles H and J are right angles. She needs to know the length of each side so she can buy fencing. What is the length of line segment FJ
Answers
The length of line segment FJ, which represents the fencing Maria needs to buy, is 24 feet.
The length of line segment FJ can be determined by using the properties of parallel lines and the properties of a rectangle.
Since sides GH and FJ are parallel, we can use the fact that opposite sides of a rectangle are congruent. Therefore, the length of line segment FJ is equal to the length of line segment GH, which is 24 feet.
To further explain, in a rectangle, opposite sides are parallel and congruent. This means that the length of one side is equal to the length of the opposite side. In this case, line segment FJ is parallel to line segment GH, and since GH measures 24 feet, FJ also measures 24 feet.
In conclusion, the length of line segment FJ is 24 feet.
Explanation: By using the properties of parallel lines and the properties of a rectangle, we can determine that the length of line segment FJ is equal to the length of line segment GH, which is 24 feet.
To know more about line segment visit:
brainly.com/question/30072605
#SPJ11
Determine which differential equation corresponds to each phase line. You should be able to state briefly how you know your choices are correct.a. dydt=3y−y2b. dydt=y(2−y)2c. dydt=y2|y−2|d. dydt=y2−3ye. dydt=4y−y3f. dydt=2y−y2g. dydt=y(y−2)h. dydt=y3−4y
Answers
to determine the stability of the equilibrium solutions Consider the autonomous differential equation
dydt=f(y).
The equilibrium solutions are obtained by solving
f(y)=0 for y.
Let
c1,c2,⋯,cn
be the equilibrium solutions.
Plot
c1,c2,⋯,cn
on the real number line, and create a phase line using the signs of
f(y)
by drawing a left arrow on the interval where
f(y)<0
, and right arrows where
f(y)>0.
Use the phase line to determine the stability of the equilibrium solutions as follows.
If both arrows point toward the equilibrium solution, it is stable.
If both arrows point away from the equilibrium solution, it is unstable.
If one arrow points towards the equilibrium solution and one points away from it, it is semi-stable.
To know more about stability of the equilibrium solutions, visit: brainly.com/question/10147176
#SPJ4
hmm need help please
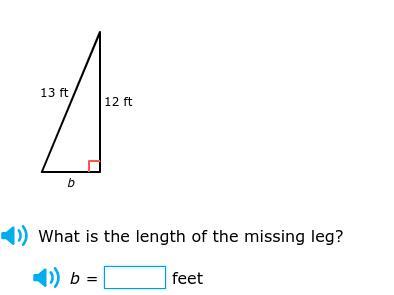
Answers
Answer:
Hello! answer: b = 5
Step-by-step explanation:
13 × 13 = 169 12 × 12 = 144 169 - 144 = 25 5 × 5 = 25 therefore b = 5 hope that helps!
13x13=169
169-144=25
5^2= 25
B=5 feet
Which number lines have points that represent additive inverses? Check all that apply
pls hurry

Answers
Answer:
B andD
Step-by-step explanation:
hope thisgives you the right answer
PLSSSSSSSS HELP ME
correct answer gets brainliest
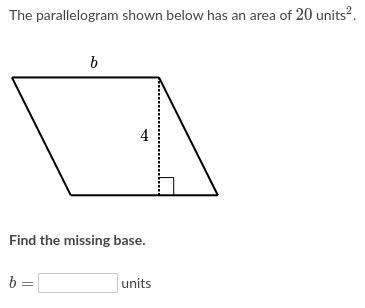
Answers
Answer:
5
Step-by-step explanation:
the area of a parallelogram is represented in this formula:
\(A=bh\)
we can rearrange this to solve for \(b\)
\(\frac{A}{h} =b\)
\(\frac{20}{4} =5\)
Therefore \(b=5\)
A box contains five keys, only one of which will open a lock. Keys are randomly selected and tried, one at a time, until the lock is opened (keys that do not work are discarded before another is tried). Let Y be the number of the trial on which the lock is opened.
a. Is a geometric distribution appropriate to use here? Why or why not?
b. Find the probability function for Y.
c. Give the corresponding distribution function.
d. What is P(Y≤4)? P(Y<4)? P(Y=4)?
e. We know that if Y is a continuous random variable, then for any constant a, P(Y=a)=0. (The probability at a single point is always zero.) Do any of your answers in (d) contradict this? Why or why not?
Answers
a. Yes, a geometric distribution is appropriate to use here because we are interested in the number of trials required to obtain the first success
b. The probability function for Y is given by:
P(Y=k) = (4/5)^(k-1) * (1/5)
c. The corresponding distribution function is given by:
F(Y≤k) = 1 - (4/5)^k
d. P(Y=4) = P(Y≤4) - P(Y<4) = 0.671 - 0.512 = 0.159
e. Even though the probability of Y taking a particular value is non-zero (in this case, P(Y=4) is non-zero), the probability of Y taking any single point value is zero (since P(Y=k)=0 for any constant k).
a. Yes, a geometric distribution is appropriate to use here because we are interested in the number of trials required to obtain the first success (opening the lock), where each trial has a constant probability of success (finding the right key) and the trials are independent.
b. The probability function for Y is given by:
P(Y=k) = (4/5)^(k-1) * (1/5)
where k is the trial number (k=1,2,3,...).
c. The corresponding distribution function is given by:
F(Y≤k) = 1 - (4/5)^k
where k is the trial number (k=1,2,3,...).
d. P(Y≤4) = F(Y≤4) = 1 - (4/5)^4 = 0.671
P(Y<4) = F(Y<4) = 1 - (4/5)^3 = 0.512
P(Y=4) = P(Y≤4) - P(Y<4) = 0.671 - 0.512 = 0.159
e. None of the answers in (d) contradict the fact that P(Y=a)=0 for any constant a, because Y is a discrete random variable and the probabilities are for intervals of values (P(Y≤k), P(Y<k), P(Y=k)) rather than single points. Even though the probability of Y taking a particular value is non-zero (in this case, P(Y=4) is non-zero), the probability of Y taking any single point value is zero (since P(Y=k)=0 for any constant k).
To learn more about probability:
https://brainly.com/question/30034780
#SPJ4
A group of 26 friend are going to travel to a fetival together, 6 of them can drive. They have a 13 peron mini-bu (1 driver 12 paenger), two car (1 driver and 4 paenger in each car) and the remaining 3 friend will take the train. The number of way in which the friend can travel (ignoring paenger eat poition within each vehicle) i a×1012. Work out the value of a. Give your anwer correct to 3 ignificant figure
Answers
If passenger seat position within each vehicle is ignoring, then the number of ways that can the friends travel is 17847429600 ways
Total number of friends = 26 friends
They have 6 seat car and 13 seat car and remaining 3 will take a bus
In the first car 6 of the 26 friends are going to sit
The combination will be
26C₆ = 230230
The combination is defined as An arrangement of object where the order in which the objects are selected doesn't matter. The combination means Selection of things, where the order of things has no importance.
In the second car 13 of 20 friends are going to sit
The combination will be
20C₁₃ = 77520
Calculate combinations, use the formula n Cr = n! / r! * (n - r)!, where n represents the total number of items, and r represents the number of items being chosen at a time. Calculate a combination, will need to calculate a factorial.
The factorial of a number is the multiplication of all the numbers between 1 and the number itself. It is written like this: n! . So the factorial of 2 is 2! (= 1 × 2).
Remaining 3 will take the train
Therefore the number of ways = 26C₆ × 20C₁₃ × 3C₃
= 230230 × 77520 × 1
= 17847429600
Hence, the number of ways that can the friends travel is 17847429600 ways.
To learn more about Combination and Factorial visit:
brainly.com/question/16745729
#SPJ4
suppose the matrix, , has eigenvectors , , and whose eigenvalues are , and respectively. then, using the same order, can be written in the form where
Answers
We can write A = PAP where 1 P= and A= where P is an invertible matrix that maps the null space of A to itself.
To find the matrix P, we need to solve the following system of linear equations:
λ_1 1 = 1
λ_2 (-4) 1 = 1
λ_3 (-1) 1 = 1
The eigenvalues are real and non-negative, so they can be written as λ = λ_1, λ_2, λ_3 = λ_1, -4, -1 respectively.
Using Cramer's rule, we have:
\(λ_1 * 1^T = 1 * 1^T = 1\)
\(λ_2 * (-4)^T = -4 * 1^T = -4\)
\(λ_3 * (-1)^T = (-1) * 1^T = -1\)
Multiplying the first and third equations, we get:
\(-λ_1 * λ_3 = -4 * (-1) = 4\)
Multiplying the second and third equations, we get:
\(-λ_2 * λ_3 = -4 * (-1) = 4\)
Subtracting the second equation from the first, we get:
\(λ_1^2 - λ_2^2 = 1^2 - (-4)^2 = 5\)
Multiplying the first and third equations, we get:
\(-λ_1 * λ_2 = -4 * (-1) = 4\)
Dividing the third equation by the second equation, we get:
\(-1/λ_2 = -1/λ_3\)
Taking the reciprocal of both sides, we get:λ_2 = λ_3
Substituting this into the second equation, we get:
-\(λ_1 * λ_3 = -4 * (-1) * λ_3 = -4\)
Simplifying, we get:
-4 = -4
This equation has no solution, so the matrix A cannot be written in the form A = PAP where 1 P= and A= Thus, the answer is no.
To know more about invertible matrix
https://brainly.com/question/31062095
#SPJ4
Full Question: the matrix, A, has eigenvectors and whose eigenvalues are 1, –4 and – 1 respectively. Then, using the same order, A can be written in the form A = PAP where 1 P= and A=
Out of a total of N students at a school, the number of students who have seen a new television program increases at a rate proportional to the product of the number of students who have seen the program and the number of students who have not seen the program. If S denotes the number of students who have seen the program at time t, which of the following differential equations could be used to model this situation, where is a positive constant? A) ks - kt ( N1) -AS (N-S) D - KS (- N)
Answers
Based on the given information, we can create a differential equation to represent the situation. Let S denote the number of students who have seen the program at time t and let N be the total number of students.
The number of students who have not seen the program is (N - S). The rate of change of students who have seen the program is proportional to the product of these two quantities, and we represent this proportionality with a positive constant k.
The differential equation to model this situation would be:
dS/dt = kS(N - S)
This equation represents the rate of change of the number of students who have seen the program (dS/dt) as proportional to the product of the number of students who have seen the program (S) and the number of students who have not seen the program (N - S), with k being the positive constant of proportionality.
To know more about differential equation visit:
https://brainly.com/question/9686230
#SPJ11
Use the given line of best fit to approximate the rate of change relative to the scatter plot below.
A.
4 hats per game
B.
3 hats per game
C.
3.75 hats per game
D.
3.25 hats per game

Answers
The correct response is C. 3.75 hats per game. The graph of the function 3.75 hats per game.
A collection of dots, lines, line segments, curves, or areas that show how one variable changes in connection to one or more other variables a grouping of all points whose coordinates meet a certain relation (such as a function)
According to the graph of the function, we know that the fitting line goes through points (3, 25) and (7, 40).
So, the rate of change is equal to 40-25/7-3=15/4=3.75
So choose A. 3.75 hats per game.
(If line goes through point \((x_{0}, y_{0})\) and point \((x_{1}, y_{1})\) Hence, its rate of change equals \(\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\) (\(x_{1}\) is not equal to \(x_{0}\)))
Learn more about graph here
https://brainly.com/question/26865
#SPJ1
A spinner is divided into 7 equal regions, numbered 9 through 15. An arrow is spun and lands on one of the numbers. Which of the following best describes the probability of the arrow landing on a number that is greater than 13?
A.
0.143
B.
0.286
C.
0.429
D.
0.571
Answers
Therefore , the solution of the given problem of probability comes out to be P =0.286(approx).
Define probability.Probability is the likelihood or potential for something to event. For instance, there is only one way to get a head and a total of two possible outcomes, hence the probability of flipping a coin and getting heads is 1 in 2. (a head or tail). P(heads) must equal 12. Classical: (equally likely results) (equally probable outcomes) S, the sample location (the collection of all distinct outcomes that could occur), Definition of Relative Frequency and Subjective Probability.
Here,
Given : S = {9,10,11,12,13,14,15}
If A is a subset of S, A could be {14,15}.
If a subset A represents the complement of spinning a number greater than 13, its sample space is A = {14,15}.
Thus,
To find the probability that it will land on number greater than 13
P = likelihood of event / total no of events
=> P = 2/7
=> P = 0.2857
=> P =0.286(approx)
Therefore , the solution of the given problem of probability comes out to be P =0.286(approx).
To know more about probability , visit
https://brainly.com/question/30034780
#SPJ1
me ayudan a resolver unos problemas en word les adjunto el archivo
Answers
What are the zeros of the function h (x) = x² + 3x - 8?
A
x = -8 and x = -2
OB
x= -8 and x = 2
cx = -2 and x = 8
OD x = 2 and x = 8

Answers
The following are the zeros for the function h (x) = x2 + 3x - 8: - x= -4 and x=2.
Describe functions.Given a collection of inputs X (domain) and a set of potential outputs Y (codomain), a function is more technically defined as a set of ordered pairings (x,y) where xX and yY with the caveat that there can only be one ordered pair with the same value of x. The function notation f:XY can be used to express that f is a function from X to Y.
The function's zero is a value of x that makes it equal to zero. In other words, the equation f(x) = 0 leads to a zero.
By putting h(x) equal to zero and figuring out x, we may determine the zeroes for the function h(x) = x2 + 3x - 8.
h(x) = x² + 3x - 8 = 0
We may factor the left side of the equation to find x:
x² + 3x - 8 = (x-2)(x+4) = 0
We set each factor to zero and solve for x to discover the zeroes:
x-2 = 0 or x+4 = 0
x = 2 or x = -4
Consequently, the function's zeros are x = 2 and x = -4.
So, A is the right response. x = -4 and x = 2
To know more about functions visit:
https://brainly.com/question/29120892
#SPJ1
The complete question is
What are the zeros of the function h (x) = x² + 3x - 8?
A. x = -4 and x = -2
B. x= -8 and x = 2
C. x = -2 and x = 8
D. x = 2 and x = 8
Each cube in the prim i one cubic unit. What i the volume of thi rectangular prim? Enter your anwer in the
Answers
Volume of the Rectangular Prim = 60 cubic units
What is Volume of the Rectangular?
The volume of a rectangular prism (V) formula is volume of a rectangular prism (V) = l w h, where. To calculate the volume of a rectangular prism, multiply its length, width, and height, which is the area of the base multiplied by its height.
volumn = L*W*H
V = 4* 3*H
Multiplying the length times and width will give us the area of the prism base. this is a 2 -dimensional measurement
multiplying the area of prism base by the height is filling up the prism or adding depth, this is what gives us the third dimension
Area of the base is 12 square unit . we multiply this by the height
A base of 4 by 3 and height 1 results in 12 cubic unit
A base of 4 by 3 and height 2 results in 24 cubic unit
A base of 4 by 3 and height 3 results in 36 cubic unit
A base of 4 by 3 and height 4 results in 48 cubic unit
A base of 4 by 3 and height 5 results in 60 cubic unit
we can say that each level of the rectangular prism contains 12 cubes. There are 5 level of 12 cubes and total of 60
i used this cube for calculation see attachment
To learn more about Rectangular visit:
brainly.com/question/21416050
#SPJ4

a sign in front of a roller coaster says "you must be 40 inches tall to ride" what percentage of this height is:
Answers
Answer: 135%
Step-by-step explanation:
Suppose that has a domain of [9,15] and a range of [1,16]. what are the domain and range of the function =4()?
Answers
The domain of g(x) is [9,15] and the range is [4,64]. The domain is the same as the original function f(x), while the range is obtained by multiplying the range of f(x) by 4.
The function g(x) = 4(f(x)) is obtained by applying a transformation to the original function f(x). Since f(x) has a domain of [9,15] and a range of [1,16], we need to determine the domain and range of g(x).
The domain of g(x) is determined by the values of x that can be plugged into f(x) without any restrictions. Since the domain of f(x) is [9,15], and g(x) applies a transformation to f(x) without affecting the domain, the domain of g(x) will also be [9,15].
The range of g(x) is determined by the values that the transformed function g(x) can take. In this case, g(x) is obtained by multiplying f(x) by 4. Multiplying f(x) by a positive constant like 4 will stretch the range of f(x) vertically. Since the range of f(x) is [1,16], multiplying it by 4 will stretch it to [4,64]. Therefore, the range of g(x) is [4,64].
In summary, the domain of g(x) is [9,15], same as the domain of f(x), and the range of g(x) is [4,64], obtained by stretching the range of f(x) by multiplying it by 4.
Learn more about Domain and range here:
brainly.com/question/30133157
#SPJ11
Which graph best represents Sarah total earnings for babysitting
Answers
Answer:
Sarah earned $10 per hour for babysitting
Step-by-step explanation:
