Corrupted by their power, the judges running the popular game show America’s Next Top Mathematician have been taking bribes from many of the contestants. During each of two episodes, a given contestant is either allowed to stay on the show or is kicked off. If the contestant has been bribing the judges, she will be allowed to stay with probability 1. If the contestant has not been bribing the judges, she will be allowed to stay with probability 1/3, independent of what happens in earlier episodes. Suppose that 1/4 of the contestants have been bribing the judges. The same contestants bribe the judges in both rounds. (a) If you pick a random contestant who was allowed to stay during the first episode, what is the probability that she was bribing the judges? (b) If you pick a random contestant, what is the probability that she is allowed to stay during both episodes? (c) If you pick a random contestant who was allowed to stay during the first episode, what is the probability that she ge
Answers
Answer:
(a) The probability that a contestant allowed to stay in the first episode is 0.5
(b) The probability that a contestant will be allowed to stay during both is 0.25
Step-by-step explanation:
The given parameters are;
The probability that a contestant who has been bribing the judges will be allowed to stay = 1
The probability that a contestant who has mot been bribing the judges will be allowed to stay = 1/3
The proportion of the contestant that has been bribing the judges = 1/4
The contestant who bribe the judges in the first round = The contestants who bribe the judges in the second round
(a) Let the total number of contestants = x
Therefore;
The number of contestants in the second round = x/4 + 1/3×(x - x/4) = x/2
Which gives that, half of the contestants make it to the second round
The probability that a contestant allowed to stay in the first episode, Pₐ₁, is given as follows;
Probability = (The number of required outcome)/(The number of possible outcome)
∴ Pₐ₁ = (x/4)/(x/2) = 2/4 = 1/2 = 0.5
The probability that a contestant allowed to stay in the first episode = 0.5
(b) The probability that a contestant will be allowed to stay during both episode, Pₐ₁₂ is given as follows;
The number of contestant that will be allowed to stay after each episode = 1/2×(The number contestant in the previous episode)
Therefore;
The number of contestant that will be allowed to stay after the first episode = 1/2 × x = x/2
The number of contestant that will be allowed to stay after the second episode = 1/2 × x/2 = x/4
Therefore, the number of contestant that will be allowed to stay after both episode = x/4
Pₐ₁₂ = (The number of contestant that will be allowed to stay after both episode)/(The total number of contestants)
∴ Pₐ₁₂ = (x/4)/x = 1/4 = 0.25
The probability that a contestant will be allowed to stay during both = 0.25.
Related Questions
The data in the table compares x, the number of pages in a chapter, to y, the amount of time, in minutes, spent reading. The function y = 0. 86x â€" 0. 09 models the data in the table. A 2-column table with 5 rows. The first column is labeled pages in a chapter with entries 10, 12, 5, 26, 20. The second column is labeled time spent reading (minutes) with entries 8, 11, 4, 22, 17. Which is the best prediction for the number of pages in a chapter that takes 18 minutes to read? 15 17 19 21.
Answers
The best prediction for the time to read 18 pages is 15 minutes
The table entry is given as:
Pages Time
10 8
12 11
5 4
26 22
20 17
From the table, 18 pages is between 12 and 20 pages.
This means that, the time to read a chapter that has 18 pages must be between the time to read a chapter of 12 and 20 pages.
It takes 11 minutes to read 12 pages, and 17 minutes to read 20 pages.
So, the time to read 18 pages must be between 11 minutes and 17 minutes.
From the given options, 15 is between 11 and 17
Hence, the best prediction for the time to read 18 pages is 15 minutes
Read more about regression at:
https://brainly.com/question/9315325
find the missing side length of a square given the area of the square

Answers
The area of a square is given by the following formula:
\(A=s^2\)To find the sidelength of the square, solve the equation for s:
\(s=\sqrt[]{A}\)Replace the given value in the equation to find the sidelength:
\(\begin{gathered} s=\sqrt[]{\frac{16}{49}} \\ s=\frac{4}{7} \end{gathered}\)The sidelength is 4/7cm.
What is the inverse of the statement?
A number that has exactly two distinct factors is prime.
If a number has exactly two distinct factors, then the number is prime.
If a number does not have exactly two distinct factors, then the number is not prime.
If a number is not prime, then the number does not have exactly two distinct factors.
If a number is prime, then the number has exactly two distinct fac
Answers
The inverse of the statement is "If a number does not have exactly two distinct factors, then the number is not prime." Thus Option 2 is the answer.
When a conditional statement is reversed, the hypothesis and conclusion are both negated. The hypothesis in the original statement is "a number with exactly two distinct factors," while the conclusion is "is prime."
To make the inverse, we negate both sections. "A number does not have exactly two distinct factors" is the antonym of "A number that has exactly two distinct factors." "Is not prime" is the opposite of "is prime."
As a result, the inverse statement is "If a number does not have exactly two distinct factors, then the number is not prime."
It's crucial to remember that a statement's inverse could or might not be accurate. In this instance, the inverse is true since the definition of a prime number is incompatible with the fact that a number has more than two components if it has more than exactly two different factors.
To learn more about the Inverse of the Statement:
https://brainly.com/question/29077755
https://brainly.com/question/28040561
complete ? m/s = 21.6 km/h
Answers
Answer:
6 m/s
Step-by-step explanation:
divide the speed value by 3.6
Answer:
6m / s
Step-by-step explanation:
21600/3600
= 6m/s
mã morse có được sử dụng trong toán học hiện nay hay không?
Answers
Answer:
zlsalzoxoxk kckenwisosoxoxo oiikqwkso ooaoqoaskxkck snsndjdixoiiwjdnrmc9oxskasmwwkdoco kzmwmed.rme99q9ss9oxxoksakwoppaxpxozkmewmwmsnsjzozokwkanakkzj i idjsmwakozoxxosmnwsoxixoiicidnenre9dxikwwks9xiwnedi9did iisiwwi ii iw99s oww9w9o sowosocoa ssozoc oqxola aocoxoq soocgsx oxbcam w a k paalvl blaxpk pink in youe area ainc aZlxldoollwkwkwsoodxoxo k kwadocemmekzxowkenfmfkskakwosks33445tmfsko
Chase has 40 m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. (The fourth side of the enclosure would be the river.) The area of the land is 168 square meters. List each set of possible dimensions (length and width) of the field.
Answers
They have a perimeter of 40 meters, and an area of 168 square meters. Therefore, either set of dimensions would work for Chase's fence.
Let's assume the rectangular plot of land has length L and width W. We can use the given information to set up the following system of equations:
2L + W = 40 (since there are three sides and the total length of fencing is 40 m)
LW = 168 (since the area of the land is 168 square meters)
Solving the first equation for W, we get:
W = 40 - 2L
we get:
L(40 - 2L) = 168
we get a quadratic equation:
\(2L^2\) - 20L + 84 = 0
Using the quadratic formula, we can solve for L:
L = (20 ± sqrt(\(20^2\) - 4(2)(84))) / (2(2))
L = (20 ± 4sqrt(11)) / 4
L = 5 ± sqrt(11)
Therefore, we have:
L = 5 + sqrt(11) or L = 5 - sqrt(11)
W = 30 - 2sqrt(11) or W = 30 + 2sqrt(11)
(5 + sqrt(11)) m by (30 - 2sqrt(11)) m
and
(5 - sqrt(11)) m by (30 + 2sqrt(11)) m
Note that both sets of dimensions satisfy the given conditions: they have a perimeter of 40 m (2L + W = 40) and an area of 168 square meters (LW = 168).
To learn more about dimensions please click on below link
https://brainly.com/question/30184380
#SPJ1
Consider the three-place Boolean function f defined by the following rule:
For each triple
(x1, x2, x3)
of 0's and 1's,
f(x1, x2, x3) = (7x1 + 2x2 + 4x3) mod 2.
(a)
Find
fâ(1, 1, 1) and fâ(0, 0, 1).
fâ(1, 1, 1)
=
fâ(0, 0, 1)
=
(b)
Describe f using an input/output table.
Input Output
x1 x2 x3 f
1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0
Answers
Considering the three-place Boolean function f defined
(a) f(1, 1, 1) = (7(1) + 2(1) + 4(1)) and f(0, 0, 1) = (7(0) + 2(0) + 4(1))
(b) Using an input/output table f is an odd parity function.
A Boolean function is a mathematical function that takes input values and returns a binary output value. In the given problem, the three-place Boolean function f is defined by the rule (7x1 + 2x2 + 4x3) mod 2, where x1, x2, and x3 are binary inputs.
To find f(1, 1, 1), we substitute x1=1, x2=1, and x3=1 in the given function. Therefore, f(1, 1, 1) = (7(1) + 2(1) + 4(1)) mod 2 = 1.
Similarly, to find f(0, 0, 1), we substitute x1=0, x2=0, and x3=1 in the given function. Therefore, f(0, 0, 1) = (7(0) + 2(0) + 4(1)) mod 2 = 0.
To describe f using an input/output table, we consider all possible input combinations of x1, x2, and x3 and evaluate the function for each combination. The resulting input/output table is as follows:
Input Output
x1 x2 x3 f
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0
From the input/output table, we can see that the function f returns 1 when the sum of 7x1, 2x2, and 4x3 is odd and returns 0 when it is even. Thus, we can conclude that f is an odd parity function.
To learn more about Boolean function, refer:-
https://brainly.com/question/27885599
#SPJ11
a spinner used in a board game is divided into 9 equally sized sectors. four of these sectors indicate that the player should move his token forward on the board, two of these sectors indicate that the player should move his token backward, and the remaining sectors award the player bonus points but do not move his token on the board. the total area of the sectors that do not allow the player to move his token is 14.6 inches squared. what is the radius of the spinner? enter your answer, rounded to the nearest tenth of an inch, in the box.
Answers
To find the radius of the spinner, we'll first find the total area of the spinner and then use the formula for the area of a circle. Radius is defined as the length between the center and the arc of circle.
Here are the steps:
1. Determine the proportion of the sectors that do not move the token: There are 3 such sectors (remaining sectors) out of a total of 9 sectors. So, the proportion is 3/9 = 1/3.
2. Calculate the total area of the spinner: Since 1/3 of the spinner has an area of 14.6 square inches, we can find the total area by multiplying the area of non-moving sectors by 3.
Total area = 14.6 * 3 = 43.8 square inches.
3. Use the formula for the area of a circle to find the radius: The formula for the area of a circle is A = πr^2, where A is the area and r is the radius. We'll solve for the radius (r) in this formula:
43.8 = πr^2
4. Divide both sides of the equation by π:
r^2 = 43.8 / π
5. Calculate r:
r = √(43.8 / π)
6. Round the result to the nearest tenth of an inch:
r ≈ 3.7 inches
So, the radius of the spinner is approximately 3.7 inches.
To learn more about “radius” refer to the https://brainly.com/question/27696929
#SPJ11
????????????????????????

Answers
Answer:
um a
Step-by-step explanation:
I'm pretty sure (98%) it is A.
Let me know if I'm wrong.
The dimension of the row space of a 3 x 3 matrix A is 2. (a) What is the dimension of the column space of A? (b) What is the rank of A? (c) What is the nullity of A? (d) What is the dimension of the solution space of the homogeneous system Ax = 0?
Answers
a) the dimension of its column space is also 2. b) the rank of A is 2. c) the nullity of matrix A is 1. d) the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
(a) The dimension of the row space of a matrix is equal to the dimension of its column space. So, if the dimension of the row space of matrix A is 2, then the dimension of its column space is also 2.
(b) The rank of a matrix is defined as the maximum number of linearly independent rows or columns in the matrix. Since the dimension of the row space of matrix A is 2, the rank of A is also 2.
(c) The nullity of a matrix is defined as the dimension of the null space, which is the set of all solutions to the homogeneous equation Ax = 0. In this case, the matrix A is a 3 x 3 matrix, so the nullity can be calculated using the formula:
nullity = number of columns - rank
nullity = 3 - 2 = 1
Therefore, the nullity of matrix A is 1.
(d) The dimension of the solution space of the homogeneous system Ax = 0 is equal to the nullity of the matrix A. In this case, we have already determined that the nullity of matrix A is 1. Therefore, the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
Know more about matrix here:
brainly.com/question/24079385
#SPJ4
descending order of 2.061,0.66,2.612,6.21,2.62
Answers
Answer:
Step-by-step explanation:
Descending order:
6.21 ; 2.62 ; 2.612 ; 2.061 ; 0.66
First see the whole number. write the number with biggest whole number.
6.21
2) Then three numbers have 2 . So, now compare the tenth place.
Two numbers have same place value 2.62 and 2.612.
Compare the hundredth place value in these two numbers.
So, 2.62
3) 2.612
4) 2.061
5) 0.66 is the smallest
A square pyramid is shown. 4 m 6 m 6 m What is the surface area of the pyramid?
Answers
Consider a population that grows according to the recursive rule Pn=Pn−1+50
, with initial population P0=30
Answers
To find the population at any given term n, continue to apply the recursive rule.
Pₙ = Pₙ₋₁ + 50
Using this recursive rule and the initial population, you can find the population at any given term n.
We are given a population growth model with a recursive rule and an initial population. Let's break down the information and find the population at any given term n.
Recursive rule: Pₙ = Pₙ₋₁ + 50
Initial population: P₀ = 30
Now let's find the population at any term n, using the recursive rule:
Step 1: Determine the base case, which is the initial population.
P₀ = 30
Step 2: Apply the recursive rule to find the next few terms.
P₁ = P₀ + 50 = 30 + 50 = 80
P₂ = P₁ + 50 = 80 + 50 = 130
P₃ = P₂ + 50 = 130 + 50 = 180
Step 3: To find the population at any given term n, continue to apply the recursive rule.
Pₙ = Pₙ₋₁ + 50
Using this recursive rule and the initial population, you can find the population at any given term n.
Learn more about recursive rule,
https://brainly.com/question/29508048
#SPJ11
Solve for x.
(2x-2)°
-(x+5)°

Answers
Answer: 29°
Step-by-step explanation:
(2x-2)° + (x+5)° + 90° = 180°
(2x-2)° + (x+5)° = 90°
(2x + x)° = 87°
(3x)° = 87°
x° = 29°
Find the length of the major arc in red

Answers
Which absolute value function, when graphed, will be wider than the graph of the parent function, f(x) = |x|?
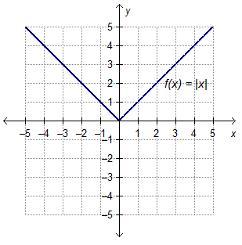
Answers
The absolute value function, when graphed, that would be wider than the graph of the parent function, f(x) = |x| is: C. f(x) = 1/3|x|.
What is an absolute value function?In Mathematics and Geometry, the vertex form of an absolute value function can be modeled as follows;
y = a|(x - h)| + k
h and k represents the vertex of the graph.a represents the leading coefficient.When the value of a is greater than 1, the graph of the parent absolute value function f(x) would be vertically stretched by factor of a, and if 0 < a < 1, the graph of the parent absolute value function f(x) would be vertically compressed vertically by a factor of 1/a.
In this context, only this absolute value function f(x) = 1/3|x| would be wider than the graph of the parent function, f(x) = |x|.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Consider the box plot below. Which of the following statements is true? A. The distribution is skewed to the right. B. The distribution is skewed to the left. C. The distribution is symmetric. D. the center of the distribution is 600.

Answers
Answer:
The distribution is skewed to the right.
Step-by-step explanation:
There are more data values to the left of the box plot, indicating that the distribution is skewed to the right.
All natural numbers excluding 1 and prime numbers are best described as?
___________________
Answers
Answer:
Composite Numbers.
find two nonnegative numbers x and y such that xy = 162 and 4x +2y is minimized.
Answers
To find two nonnegative numbers x and y such that xy = 162 and 4x +2y is minimized, we need to use the concept of the Arithmetic-Geometric Mean.The main answer is:x = 9√2y = 9/√2
Explanation: Arithmetic-Geometric Mean: Let a and b be positive numbers.The Arithmetic Mean (AM) is a + b / 2. The Geometric Mean (GM) is √ab.The Arithmetic-Geometric Mean is the following:a_n = (a_n−1 + b_n−1) / 2 b_n = √a_n−1 * b_n−1 a_0 = a b_0 = b
Let's solve the problem using the Arithmetic-Geometric Mean.√(4xy) = √(4 * 162) = 36xy/36 = 162/36xy = 9√2 * 9/√2xy = 81The numbers that will minimize 4x + 2y are 4x = 36, and 2y = 18. Therefore, x = 9√2, and y = 9/√2
To know more about Geometric visit:
https://brainly.com/question/29170212
#SPJ11
Solve
5x - 4 = 3x + 12.
Answers
Answer:
x=8
Step-by-step explanation:
5x-4=3x+12
-3x. -3×
2x-4=12
+4. +4
2×=16
÷2. ÷2
x=8
Formula: \(t = 50 + \frac{n - 40}{4} \)Where T is temperature in Fahrenheit and N is a number of chirps per minute. If T=60°F, find the number of chirps per minute.
Answers
In order to find the value of N in the equation when T = 60, we just need to apply the value of T and then calculate the value of N.
So we have that:
\(\begin{gathered} T=50+\frac{N-40}{4} \\ 60=50+\frac{N-40}{4} \\ \frac{N-40}{4}=10 \\ N-40=40 \\ N=80 \end{gathered}\)So the number of chirps per minute is 80
Suppose that 2 ≤ f '(x) ≤ 4 for all values of x. What are the minimum and maximum possible values of
f(5) − f(1)?
Answers
Answer:
Step-by-step explanation:
By the Mean Value Theorem, there is at least one number, c, in the interval (1,6) such that
f'(c) = [f(6) - f(1)]/ (6 - 1)
So, f(6) - f(1) = 5f'(c).
Since 2 ≤ f'(c) ≤ 4, 10 ≤ 5f'(c) ≤ 20
So, f(6) - f(1) is between 10 and 20.
Determine the value of the 10% trimmed mean. (Round your answer to four decimal places.)
0.2, 0.21, 0.26, 0.3, 0.33, 0.41, 0.54, 0.57, 1.41, 1.7, 1.84, 2.2, 2.26, 3.06, 3.24
Answers
The value of the 10% trimmed mean is approximately 1.3027. To calculate the 10% trimmed mean, we need to trim off the lowest and highest 10% of the data and then find the mean of the remaining values.
First, let's sort the data in ascending order:
0.2, 0.21, 0.26, 0.3, 0.33, 0.41, 0.54, 0.57, 1.41, 1.7, 1.84, 2.2, 2.26, 3.06, 3.24
Next, we calculate the number of values to trim from each end:
10% of 15 (total number of values) = 0.1 * 15 = 1.5
Since we can't remove half a value, we round up to the nearest whole number, which is 2.
Now, we remove the two lowest and two highest values:
0.26, 0.3, 0.33, 0.41, 0.54, 0.57, 1.41, 1.7, 1.84, 2.2, 2.26
Finally, we calculate the mean of the remaining values:
(0.26 + 0.3 + 0.33 + 0.41 + 0.54 + 0.57 + 1.41 + 1.7 + 1.84 + 2.2 + 2.26) / 11 = 14.33 / 11 ≈ 1.3027
Rounding to four decimal places, the value of the 10% trimmed mean is approximately 1.3027.
To know more about statistics refer here;
https://brainly.com/question/32201536?#
#SPJ11
20 The second term of a geometric sequence is 14.5 and the fifth
term is 1.8125
a Determine the common ratio,
b Find the value of the first term.
€ Find the sum of the first 5 terms,
Answers
Answer:
a. The common ratio is 0.5
b) The value of the first term is 29
c) The sum of the first 5 terms is 56.1875
Step-by-step explanation:
The nth term of the geometric sequence is a\(_{n}\) = a\(r^{n-1}\), where
a is the 1st termr is the common ratioThe sum of the nth term is S\(_{n}\) = \(\frac{a(1-r^{n})}{1-r}\)
∵ The second term of a geometric sequence is 14.5
∴ n = 2
∴ a\(_{2}\) = 14.5
∵ a\(_{2}\) = ar
→ Equate the right sides of a\(_{2}\) by 14.5
∵ ar = 14.5 ⇒ (1)
∵ The fifth term is 1.8125
∴ n = 5
∴ a\(_{5}\) = 1.8125
∵ a\(_{5}\) = a\(r^{4}\)
→ Equate the right sides of a\(_{5}\) by 14.5
∵ a\(r^{4}\) = 1.8125 ⇒ (2)
→ Divide equation (2) by equation (1)
∵ \(\frac{ar^{4}}{ar}\) = \(\frac{1.8125}{14.5}\)
∴ r³ = 0.125
→ Take ∛ for both sides
∴ r = 0.5
a. The common ratio is 0.5
→ Substitute the value of r in equation (1) to find a
∵ a(0.5) = 14.5
∴ 0.5a = 14.5
→ Divide both sides by 0.5
∴ a = 29
b) The value of the first term is 29
∵ n = 5
∴ S\(_{5}\) = \(\frac{29[1-[0.5]^{5})}{1-0.5}\)
∴ S\(_{5}\) = 56.1875
c) The sum of the first 5 terms is 56.1875
Consider the following piece-wise defined function (e is an unspecified constant). f(x)= - x+3 if x < 3 √x² + c if x ≥ 3 Find a value of e such that the function f(x) is continuous at x = 3. (5) Let f(x)= x³ + 2x - 2. (a) Use the Intermediate Value Theorem (stated below) to show that the equation f(x) = 0 has a solution in the interval (-1,1). (In other words, f had a root strictly between -1 and 1.) (b) What property of this function f allows us to use the Intermediate Value Theorem? (c) The Intermediate Value Theorem guarantees that the equation f(x) = 0 has at least one solution in the interval (-1,1). But in this case, it turns out that there is exactly one solution. How can you show that there is exactly one solution using other techniques from Calculus?
Answers
a) Let's evaluate f(-1) and f(1): f(-1) = (-1)³ + 2(-1) - 2 = -1 - 2 - 2 = -5
f(1) = (1)³ + 2(1) - 2 = 1 + 2 - 2 = 1
Since f(-1) = -5 < 0 and f(1) = 1 > 0, by the Intermediate Value Theorem, there exists a value c in the interval (-1,1) such that f(c) = 0.
b) The function f(x) = x³ + 2x - 2 is a polynomial function, and polynomial functions are continuous over their entire domain. Therefore, the function f satisfies the continuity requirement of the Intermediate Value Theorem.
c) To show that there is exactly one solution to the equation f(x) = 0, we can analyze the behavior of the function using calculus techniques. For instance, by finding the derivative f'(x) = 3x² + 2 and observing its sign changes, we can conclude that there is a single root within the interval (-1,1). Additionally, we can apply the Mean Value Theorem, which guarantees that if a function is continuous on a closed interval and differentiable on the open interval, there exists at least one point in the open interval where the derivative is equal to the average rate of change over the closed interval. By analyzing the behavior of the derivative, we can show that there is exactly one solution within the interval (-1,1).
To know more about Intermediate Value Theorem click here: brainly.com/question/29712240
#SPJ11
YALL I NEED HELP PLS THIS IS DUE SOON
when Rachel exceeds the number of minutes on her cell phone plan,she is charged an extra cost for each minute. The graph below show the total cost (y), in dollars,for exceeding her cell phones plans minutes by x minutes.
Answer options:
Number of Minutes
What does the y-coordinate represent when the x-coordinate has a value of 1?
1. Rachel pays $0.25 for each minute she exceeds her cell phone plan's muutes
2. Rachel pays $0.50 for each marute she exceeds her cell phone plan's minutes
3. Rachel pays $1.00 for each minute she exceeds her cell phone plan's minutes
4. Rachel pays $4.00 for each minute she exceeds her cell phone plan's mimates

Answers
Answer: If you look at the x axis 1 is less than $1 so if you follow the x axis to the right until you find a number of minutes that meets the y axis of $1 so x4, y1 that means $.25 per minute if you divide 1 by 4. So 1 is the correct answer.
Step-by-step explanation:
1. Follow the x axis until the x and y axis meet. This is $1.00 on the y axis.
2. Then you would divide 1 by 4 and you get .25. Each minute would be $.25.
find an equation of the tangent line to the curve xe^y + ye^x = 2 at the point (0, 2).
Answers
Therefore, the equation of the tangent line to the curve xe^y + ye^x = 2 at the point (0, 2) is y = -x + 2.
To find an equation of the tangent line to the curve xe^y + ye^x = 2 at the point (0, 2), we need to use the concept of differentiation.
First, we differentiate both sides of the equation with respect to x using the product rule and the chain rule:
(d/dx)[xe^y] + (d/dx)[ye^x] = (d/dx)[2]
e^y + xe^y(dy/dx) + e^x(dy/dx) + ye^x = 0
Simplifying this expression and evaluating it at the point (0, 2), where x = 0 and y = 1, we get:
e^1 + 0 + e^0(dy/dx) + 2e^0 = 0
dy/dx = -1
Therefore, the slope of the tangent line at the point (0, 2) is -1.
Next, we can use the point-slope form of a line to find the equation of the tangent line. We know the slope is -1 and the point (0, 2) lies on the line, so we can write:
y - 2 = -1(x - 0)
Simplifying this expression, we get:
y = -x + 2
To know more about tangent line,
https://brainly.com/question/28089413
#SPJ11
Please help me this is urgent

Answers
Answer:
A) C (15:30) B) D (16km)
Step-by-step explanation:
A)
Look along x-axis which is time the dotted whish is of bethan
journey finished between 14:00 to 16:00
The ending point is 3 boxes forwad to 14:00 and each box represent 30 min
So time is 15:00
B)
Look at y-axis which is distance
Journey start from 0 to 8 then take time and again start from 8 to final point
When addedup it equal t0 16km
Mark brainliest if you understand
Find the unit tangent vector t(t) at the point with the given value of the parameter t. r(t) = 4 t i 3t2 j 3t k, t = 1
Answers
The unit tangent vector t(1) at t = 1 is:
t(1) = (4 i + 6 j + 3 k) /\(\sqrt{(61)}\)
To find the unit tangent vector,
we need to calculate the derivative of the position vector r(t) with respect to the parameter t, and then normalize the resulting vector.
Given the position vector r(t) = 4t i + 3t^2 j + 3t k,
we can find the derivative:
r'(t) = d(r(t))/dt
= 4 i + 6t j + 3 k
Now, we can evaluate r'(t) at t = 1:
r'(1) = 4 i + 6(1) j + 3 k
= 4 i + 6 j + 3 k
To obtain the unit tangent vector,
we need to normalize r'(1):
t(1) = r'(1) / ||r'(1)||
where ||r'(1)|| represents the magnitude or length of r'(1).
The magnitude of r'(1) is given by:
||r'(1)|| = \(\sqrt{((4^2) + (6^2) + (3^2))}\)
= \(\sqrt{61}\))
This is the normalized vector representing the direction of the tangent to the curve at the point where t = 1.
Learn more about Vectors here:
https://brainly.com/question/31900604
#SPJ11
Find the average rate of change of g(x)=
–
12x+1 over the interval [
–
7,
–
1].
Answers
Answer:
12
Step-by-step explanation:
average rate
\(=\frac{g(-1)-g(-7)}{-1-(-7)} \\=\frac{[12(-1)+1]-[12(-7)+1]}{-1+7} \\=\frac{[-12+1]-[-84+1]}{6} \\=\frac{-11+83}{6} \\=\frac{72}{6} \\=12\)