Answers
Answer: 73.5
first you work out the total area of this shape.
area: 105
this mean you can start working out the non-shaded area to do this you need to multiply 7cm with 6cm which is 42cm then you divide by 2 to get 21cm.
then to work ou the other non-shaded area in the left you multiply 3cm and 7cm together getting 21cm you then divide it and you get 10.5.
you then add 10.5cm and 21cm together to get 31.5cm, subtract that answer with the total area which gets the answer 73.5!
Related Questions
Find the probability of rolling a prime number when a 16-sided die is rolled.
A) 5/16
B) 3/8
C) 7/16
D) 1/16

Answers
Answer:
6/16
Step-by-step explanation:
On a 16 sided die there would be number as follows :
1,2,3,.. 16 The prime number out in this set of numbers are
2,3,5,7,11, and 13
There are 6 prime number so the probability of rolling a prime number is
6/16
Step-by-step explanation:
If the given dice is 16-sided, then it would contain following numbers:-
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16
We know that, the numbers which aren't divisible by any numbers except itself and 1 are prime numbers.
Out of 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16
the prime numbers are as follow:-
2,3,5,7,11,13
Here, the number of prime numbers are 6,
Therefore, the probability of rolling a prime number when the dice is rolled is
6/16=3/8Hence, option B. is the correct answer.
Which statistic (mean, median, or mode) is most appropriate in each of the following situations?
The offensive line of a football team is larger than the previous years. The program will list a statistic to show this fact.
• Mean
• Median
• Mode
Answers
Answer:
Step-by-step explanation: In this situation, mean would be the most appropriate statistic to show the increase in the size of the offensive line of the football team. The mean is a measure of central tendency that takes into account all the values in a set and calculates the average, giving a good representation of the general trend of the data. The mean size of the offensive line can be calculated by adding up the size of all the players and dividing by the number of players. This would give a good idea of the overall increase in the size of the offensive line.
Maricopa's Success scholarship fund receives a gift of $ 145000. The money is invested in stocks, bonds, and CDs. Stocks pay 6.7 % interest, bonds pay 2.5 % interest, and CDs pay 5.75 % interest. Maricopa Success invests $ 10000 more in bonds than in CDs. If the annual income from the investments is $ 6977.5 , how much was invested in each account?
Maricopa Success invested $ in stocks.
Maricopa Success invested $ in bonds.
Maricopa Success invested $ in CDs.
Answers
Answer:
stocks: $45000bonds: $55000CDs: $45000Step-by-step explanation:
You want to know the amounts invested in stocks, bonds, and CDs when the total investment is $145000, $10000 more is invested in bonds than CDs, earnings are $6977.50, and rates of return are 6.7% for stocks, 2.5% for bonds, and 5.75% for CDs.
SetupWe can write three equations in 3 unknowns for this problem. Let s, b, c represent amounts invested in stocks, bonds, and CDs, respectively. Then the problem statement tells us the relations are ...
s + b + c = 145000b - c = 100000.067s +0.025b +0.0575c = 6977.50SolutionThese equations can be solved using any of several methods. The second equation offers a nice relation between b and c, so substitution for one or the other of those will reduce the equations to two equations in two unknowns.
We prefer a calculator solution using an augmented matrix of the coefficients. That is shown in the attachment. It tells us the investment amounts are ...
stocks: $45000bonds: $55000CDs: $45000__
Additional comment
Using b = c +10000, the two remaining equations are ...
s +2c = 1350000.067s +0.0825c = 6727.50<95141404393>

2x² + 10 factorización
Answers
Answer:
2(x² + 5)
Step-by-step explanation:
To factor 2x² + 10, we can first factor out the greatest common factor of the terms, which is 2:
2x² + 10 = 2(x² + 5)
We can't factor anymore, so the answer is:
2(x² + 5)
Answer:
2(x² + 5)
Step-by-step explanation:
To factorise this, do the distributive property backwards. In other words:
2x² + 10
2x² ÷ 2 + 10 ÷ 2
x² + 5
2(x² + 5)
∴ 2(x² + 5) is the answer
Ahmad and Daryl had an equal amount of money at first. Ahmad's father gave him another $180, and Daryl spent $255. Ahmad then had 4 times as much money as Daryl. How much money did each of them have at first?
Answers
Answer:
$400
Step-by-step explanation:
Suppose Ahmad and Daryl both started with the same x amount of dollars.
Ahmad gains another 180 from his father, so he now has x+180 dollars.
Daryl spends 255, so he now has x-255 dollars.
After these events, Ahmad has 4 times as much money as Daryl, so
x+180=4(x-255)
Now we can solve for x to get the original amount of money.
x+180=4(x-255)
x+180=4x-1020
1200=3x
x=400
Both Ahmad and Daryl started with $400.
Internet sites often ask for a secret phrase to recover lost passwrds. Jason encoded a secret phrase using matrix multiplication. He multiplied the clear text code for each letter by the matrix:
The matrix representing the encoded text is:
Jason’s secret phrase is:
Clear text encoding:
Decoding a Message by Finding An Inverse

Answers
Answer:
cats rule dogs drool is correct ty<3
Step-by-step explanation:
Answer:
cats rule dogs drool
Step-by-step explanation:
just did it edge23
-12 = 4 + c
mmmmmmmmmmmmmmm
Answers
Answer:
c=-16
Step-by-step explanation:
-12=4+c
-4=-4
-16=c
Answer:
-16
Step-by-step explanation:
the reason is because -12 -4 is -16 so when you add -16 to 4 you get -12
have a nice day
If x=|9|what are the possible values of x?
Answers
Answer:
9
Step-by-step explanation:
the absolute value function always delivers only the positive value of anything inside the absolute function.
therefore, x is 9 and only 9.
Shelton mix 1 1/4 cups of purple cabbage and
2 3/8 cups of lettuce to make a big salad. Each day he eats 3/4 of a cup is salad.

Answers
Answer:
Its the bottom one.
Step-by-step explanation:
Answer: ( 1 1/4 + 2 3/8 ) 3/4
Step-by-step explanation:
This is the answer
Given f(-8) = 0 (-8 is a root) and f(5) = 0 (5 is a root), which of these expressions could
possibly be the factored form of the polynomial?

Answers
Given f(-8) = 0 (-8 is a root) and f(5) = 0 (5 is a root), then option d (x+8)(x-5) is the factor form.
What is Polynomial?Polynomials are sums of terms of the form k⋅xⁿ, where k is any number and n is a positive integer.
Given that f(-8) = 0 (-8 is a root) and f(5) = 0 (5 is a root),
Minus eight and plus five are two roots of which expression we have to find.
Among the given options
(x+8)(x-5) is the expression
When we solve this
x+8=0
x=-8
Which is one of the required root
x-5=0
x=5 which is other root.
Hence (x+8)(x-5) is the required factored form of the polynomial
To learn more on Polynomials click:
https://brainly.com/question/11536910
#SPJ1
Use trigonometric identities to solve the trigonometric equation sin(2∅)-cos(∅)=0 for 0≤∅≤2π. You must show all of your work analytically.
Answers
Step-by-step explanation:
sin(2x) = 2sin(x)cos(x)
2sin(x)cos(x) - cos(x) = 0
so one solution is cos(x) = 0.
=> x = pi/2 and 3pi/2 (90° and 270°)
for cos(x) <> 0 we have then
2sin(x) - 1 = 0
2sin(x) = 1
sin(x) = 1/2
=> x = pi/6 and 5pi/6 (30° and 150°)
Point-slope equation
y-6=3(x - 5)
y- 4 = -9(x+8)
y- 2 = 5x
Slope
-10
2
712
2
Point on
line
(1,4)
(5,-3)
(-7,-7)

Answers
The point slope equation and slope of some lines are given below
1) For y - 6 = 3(x - 5), slope = 3
2) For y - 4 = -9(x + 8), slope = -9
3) y - 2 = 5x, slope = 5
4) Point slope equation of line whose slope = -10 and passing through (1, 4)
y - 4 = -10(x - 1)
5) Point slope equation of line whose slope = 2 and passing through (5, -3)
y + 3 = 2(x - 5)
6) Point slope equation of line whose slope = \(\frac{1}{2}\) and passing through (-7, -7)
\(y +7 = \frac{1}{2}(x +7)\\\)
What is equation of line in point slope form?
The most general form of equation of line in point slope form is given by \(y - y_1 = m(x - x_1)\) , \((x_1, y_1)\) is a point on the line
Where m is the slope of the line
Slope of a line is the tangent of the angle that the line makes with the positive direction of x axis.
If \(\theta\) is the angle that the line makes with the positive direction of x axis, then slope (m) is given by
m = \(tan\theta\)
1) y - 6 = 3(x - 5)
y - 6 = 3x - 15
y = 3x - 15 + 6
y = 3x - 9
Slope = 3
If x = 0,
\(y = 3 \times 0 -9\\y = -9\)
(0, -9) is a point on the line
2) y - 4 = -9(x + 8)
y - 4 = -9x - 72
y = -9x - 72 + 4
y = -9x - 68
Slope = -9
If x = 0
\(y = -9 \times 0 -68\\y = -68\)
(0, -68) is a point on the line
3) y - 2 = 5x
y = 5x + 2
Slope = 5
Putting x = 0
\(y = 5 \times 0 + 2\\y = 2\)
(0, 2) is a point on the line
4) Slope = - 10
The line passes through (1, 4)
Point slope equation
y - 4 = -10(x - 1)
5) Slope = 2
The line passes through (5, -3)
Point slope equation
y - (-3) = 2(x - 5)
y + 3 = 2(x - 5)
6) Slope = \(\frac{1}{2}\)
The line passes through (5, -3)
Point slope equation
\(y - (-7) = \frac{1}{2}(x - (-7))\\y +7 = \frac{1}{2}(x +7)\\\)
To learn more about point slope equation and slope, refer to the link-
https://brainly.com/question/24907633
#SPJ9
What is the equation for Chin’s charges needed to solve the system and find the cost of the initial and additional hours?
Answers
The equation, in slope-intercept form is y = 0.75x + 1.75
How to determine the equation, in slope-intercept formThe equation for total cost can be represented in slope-intercept form as:
y = mx + b
where y is the total cost, x is the number of tacos,
m is the slope (the cost per taco), and b is the y-intercept (the cost of the drink).
So in this case,
m = 0.75 (the cost per taco),
b = 1.75 (the cost of the drink), and
x is the number of tacos.
So, the equation is:
y = 0.75x + 1.75
Read more about linear equation at
https://brainly.com/question/15602982
#SPJ1
Complete question
Chin is sells food at a local taco truck. She sells a soda which costs $1.75. Tacos cost $0.75 each.
What is the equation for Chin’s charges needed to solve the system and find the cost of the initial and additional hours?
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

An internet company randomly selected 50 of its
customers and asked them how many hours per
week they use the internet. Of those surveyed, 28
use the internet more than 15 hours per week.
Based on the data, if the company has 800
subscribers how many watch more than 10 hours
per week?
Answers
Answer:
448 subscribers
Step-by-step explanation:
First, find the percentage of people that use the internet more than 15 hours per week.
\(\%=\frac{28}{50}=0.56=56\%\)
Now, we can use this information to find 56% of 800.
\(56\%*800\)
Note that percentages can also be written as that number over 100.
\(\frac{56}{100}*800=\frac{44800}{100}=448\text{ subscribers}\)
I'm so lost on this work

Answers
Answer:
Typist A can type faster
Step-by-step explanation:
Replace the t in w = 50t with any numbers and graph the points you get
You can see that typist A can type 50 words per minute when typist B can only type 40
PLLLLLEASEEEEEEEED HELP IM BEGGING SOMEONE PLEASEEEEEEEEES

Answers
Answer:
The measure of angle D and A must be equal.
Step-by-step explanation:
ASA means angle-side-angle. So you must have two angles and the side between them be congruent to the other triangle. We already know Angle C and F are congruent and Side lengths AC and FD are congruent. So we just need the angles on the other side of the side lengths.
4. An equilateral triangle has a perimeter of 60 cm. Find the exact
altitude of the triangle.
Answers
Step-by-step explanation:
GIVEN:-The Perimeter of Equilateral triangle = 60cm
UNDERSTANDING THE CONCEPT:-According to the question,
To find the height of the triangle,
Perimeter of Equilateral triangle = Area of Equilateral triangle.
FORMULA USED:-\(60 = \frac{ \sqrt{3} }{4} a {}^{2} \\ \)
REQUIRED ANSWER:-\(60 \times 4 = \sqrt{3a {}^{2} } \)
\(a {}^{2} = 240 \sqrt{3} \\ \)
\(a = 120 \sqrt{3} cm\)
SO, The Exact height of the triangle is 120√3cm.) In a geometric progression, the sum of the first two terms is equal to 16. The sum to infinity is equal to 25. Find the possible values of the first term.
Answers
There are no possible real values for the first term 'a' that satisfy both equations.
Let's denote the first term of the geometric progression as 'a' and the common ratio as 'r'.
The sum of the first two terms can be expressed as:
a + ar = 16
To find the sum to infinity, we can use the formula:
Sum to infinity = a / (1 - r)
Given that the sum to infinity is 25, we have:
25 = a / (1 - r)
We now have two equations:
a + ar = 16
a / (1 - r) = 25
We can solve these equations simultaneously to find the possible values of 'a'.
From the first equation, we can factor out 'a' to get:
a(1 + r) = 16
Dividing both sides of the second equation by 25, we have:
a / (1 - r) = 1
We can rearrange this equation to get:
a = 1 - r
Substituting this expression for 'a' in the first equation, we get:
(1 - r)(1 + r) = 16
Expanding the equation, we have:
1 - r^2 = 16
Rearranging the terms, we get:
r^2 = -15
Since we are dealing with a geometric progression, the common ratio 'r' must be a real number. However, we observe that r^2 = -15 has no real solutions. Therefore, there are no possible real values for the first term 'a' that satisfy both equations.
for such more question on real value
https://brainly.com/question/27371101
#SPJ8
Five of the 100 digital video recorders (DVRs) in an inventory are known to be defective. What is the probability that a
randomly selected item is defective?
Answers
Answer:
1:20
Step-by-step explanation:
Because it's maths duhh
what is an acid or a base
Answers
an acid is a substance that donates protons ( in the brønsted - lowry definatiom) or accepts a pair of balance electrons to form a bond ( in the Lewis definition ) .
A base is a substance that can accept protons or donate a pair of valence electrons to form a bond . bases can be thought of as the chemical opposite if acids .
hope this helps you
mrk me braniliest plz
Answer:
a acid is a substance that can donate protons . or accepts the balance protons to form a bond .
a base is a substance that can accept protons or donate a pair of valence electrons to form a bond .
4 3/8 + 5 1/2= in fractions
Answers
Answer:
9 7/8
Step-by-step explanation:
1. 4 3/8 can be converted into the improper fraction 35/8, and 5 1/2 can be converted into 11/2.
2. Now that we have 35/8 + 11/2, we have to find a common denominator. Since 2 goes into 8 four times, we can turn 11/2 into 44/8 by multiplying the numerator and denominator (the top and the bottom numbers) by 4.
3. Now we have 35/8 + 44/8. At this point, the all we have to do is add the numerators (the top numbers). 35+44=79, so our answer is 79/8, which we can simplify to 9 7/8.
Please please help me on this one!

Answers
Answer:
3422 x232
Step-by-step explanation:
I give you brainless if you get it right

Answers
Which of the following is the formula used to calculate the variance of a set
of data?

Answers
The formula used to calculate the variance of a set of data is Variance = \(s^2\)=1n−1n∑i=1(xi−¯x\()^2\).(Option-A)
To calculate the variance, each data point is subtracted from the mean, squared, and then added together. This gives the sum of the squared deviations from the mean. This sum is then divided by the total number of data points to get the average squared deviation from the mean, which is the variance.
Variance is a measure of the spread or variability of a set of data. It is useful in statistical analysis to understand how much the data points differ from the mean, and to compare different sets of data. Lower variance values indicate that the data is more tightly clustered around the mean, while higher variance values indicate that the data is more spread out.(option-A)
For such more questions on variance
https://brainly.com/question/25639778
#SPJ8
Listed below is a table showing the number of employees. 20 years or older by gender in the United states
Answers
The total number of workers that were studied can be found to be 139,340,000.
The percent of workers unemployed would be 5. 4 %.
Percentage of unemployed men is 5. 6 % and unemployed women is 5. 1%.
How to find the employment figures ?Number of employed workers :
= 74,624,000 + 64, 716, 000
= 139,340,000
Percentage unemployed :
= ( 4, 209,000 + 3,314,000 ) / 139,340,000
= 5. 4 %
Percentage of unemployed men :
= 4,209,000 / 74,624,000
= 5.6 %
Percentage of unemployed women:
= 3,314,000 / 64, 716, 000
= 5. 1 %
Find out more on unemployment at https://brainly.com/question/13280244
#SPJ1
The full question is:
a. How many workers were studied?
b. What percent of the workers were unemployed?
c. Compare the percent unemployed for the men and the women.

Triangle JKL has vertices at J(−1, −5), K(−2, −2), and L(2, −4). Determine the translation direction and number of units of the image of triangle JKL if vertex J′ is at (−3, −5).
4 units down
4 units up
2 units to the right
2 units to the left
Answers
A triangle JKL has vertices at J(−1, −5), K(−2, −2), and L(2, −4) and J′ at (−3, −5). The translation direction is 2 units to the left. The number of units of the image of triangle JKL is 2 units to the left only.
Given that a triangle JKL has vertices at J(−1, −5), K(−2, −2), and L(2, −4) and J′ at (−3, −5). We have to determine the translation direction and the number of units of the image of triangle JKL. Let's first find the translation direction to determine the image of triangle JKL.
Seeing the position of J and J', we can determine that the translation was made in the left direction because J has moved from the point (-1,-5) to (-3,-5). Thus, the translation direction is 2 units to the left. Now, let's calculate the number of units of the image of triangle JKL.
Let's draw a rough sketch of the triangle JKL and locate its vertices J(-1,-5), K(-2,-2), and L(2,-4).To find the number of units of the image of triangle JKL, we need to find the horizontal and vertical distances between the vertices of the original triangle and its image.
We can use the horizontal distance between J and J′ as a reference to calculate the remaining distances. J has moved 2 units to the left, so the horizontal distance between J and J′ is 2. Now, let's calculate the vertical distance between J and J′. The coordinates of J and J′ are (-1,-5) and (-3,-5), respectively.
The difference between the y-coordinates of J and J′ is 0, which means that J and J′ are on the same horizontal line. Therefore, the vertical distance between J and J′ is 0. Hence, the image of the triangle JKL has moved 2 units to the left and 0 units vertically. Thus, the number of units of the image of triangle JKL is 2 units to the left only.
For more questions on the triangle
https://brainly.com/question/17335144
#SPJ8
Please help me in confused

Answers
Answer:
20\(c^{6}\)
Step-by-step explanation:
using the rule of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
given
(- 4c³)(- 5c³) ← remove parenthesis
= - 4 × c³ × - 5 × c³
= - 4 × - 5 × c³ × c³
= 20 × \(c^{(3+3)}\)
= 20\(c^{6}\)
The table shows the monthly rainfall at a measuring station. What is the mean monthly rainfall? Round your answer to the nearest thousandth.
Answers
The mean monthly rainfall, Rounded to the nearest thousandth, is 2.520 inches.
To determine the mean monthly rainfall, we need to calculate the average of the rainfall values provided in the table. Here is the table:
| Month | Rainfall (in inches) |
|-------|----------------|
| January | 2.3
| February | 1.7
| March | 3.2
| April | 2.9
| May | 2.5
To find the mean monthly rainfall, we add up the rainfall values for each month and divide the sum by the total number of months. In this case, we have five months:
Mean Monthly Rainfall = (2.3 + 1.7 + 3.2 + 2.9 + 2.5) / 5
Calculating the sum of the rainfall values:
Mean Monthly Rainfall = 12.6 / 5
Dividing the sum by the number of months:
Mean Monthly Rainfall = 2.52
Rounded the result to the nearest thousandth, the mean monthly rainfall is approximately 2.520 inches.
Therefore, the mean monthly rainfall, rounded to the nearest thousandth, is 2.520 inches.
To know more about Rounded .
https://brainly.com/question/30545728
#SPJ8
Find the Area of the Shaded Region Below 21" Submit Question
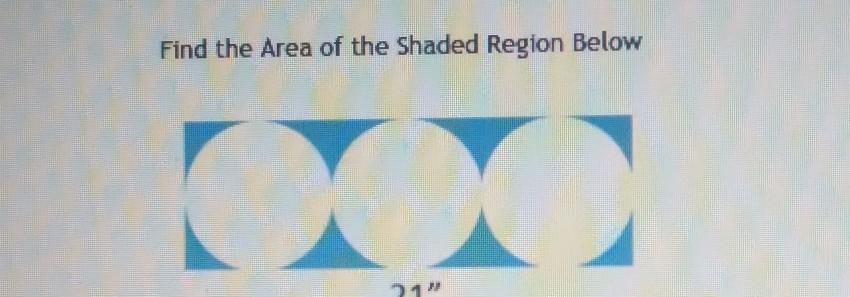
Answers
Let's begin by identifying key information given to us:
The length of the 3 squares = 21 in; each square = 7 in
The figure is that of three circles inscribed in 3 squares. To find the area of the shaded portion, we will find the difference between the area of the square & the area of the circle
This is shown below:
\(undefined\)