dave has built a storage box and needs to decorate it. It is cuboid 32cm long, 20cm wide and 30 cm tall. what is the volume of daves storage box and what is the surface area?
Answers
The volume of Daves storage box is 19200 and the surface area is 4400
What is the volume of daves storage box and what is the surface area?The given parameters are
Length = 32 cm
Width = 20 cm
Height = 30 cm
The volume is
Volume = Length * width * height
So, we have
Volume = 32 * 20 * 30
Evaluate
Volume = 19200
The surface area is
A =2 *(LW + LH + WHW)
So, we have
A = 2 * (32 * 20 + 20 * 30 + 32 * 30)
Evaluate
A = 4400
Hence, the volume of Daves storage box is 19200 and the surface area is 4400
Read more about volume at:
https://brainly.com/question/463363
#SPJ1
Related Questions
Which of the following points is in the solution set of y < x2 - 2x - 8? O 1-2. -1) O 10.-2) 0 (4.0)

Answers
Given the functon
\(yExplanation
To find the points that lie in the solution set we will lot the graph of the function and indicate the ordered pirs.
From the above, we can see that the right option is
Answer: Option 1

Brainly for the one who help me
the words choices is
Fortunately
Obviously
Suddenly
Eventually

Answers
Answer:
suddenly
Step-by-step explanation:
Answer:
Suddenly is the answerStep-by-step explanation:
Suddenly is a quickly and without warning or unexpectedly.Example:Suddenly I heard a loud scream.Combine like terms to write an equivalent expression. Then use y = 5 to prove the expressions are equivalent. 1 + y + y + y + 1 Complete the statements.
The equivalent expression is . The value of both expressions when y = 5 is . The expressions are .
Answers
Answer:
The equivalent expression is
✔ 3y + 2
.
The value of both expressions when y = 5 is
✔ 17
.
The expressions are
✔ equivalent
.
Step-by-step explanation:
Answer:
The equivalent expression is
✔ 3y + 2
.
The value of both expressions when y = 5 is
✔ 17
.
The expressions are
✔ equivalent
.
Step-by-step explanation:
An official playing field (including end zones) for the Indoor Football League has a length 30 yd longer than its width.
The perimeter of the rectangular field is 164 yd. Find the length and width of the field.
Answers
The length and width of the rectangular playing field are 56 yard and 26 yard respectively.
Explain the term perimeter of rectangle?A rectangle's perimeter (P) is the sum of the lengths of its four sides. A rectangle contains two equal lengths plus two equal widths since its opposite sides are equal. Below is the equation for calculating a rectangle's perimeter: perimeter = length + length + width + width.For the stated question-
Let the length of the football league be 'L'.
Let the width of the football league be 'B'.
Then, L = 30 + W
Perimeter = 164 yards.
Perimeter = 2(L + W)
Perimeter = 2(30 + W + W)
Perimeter = 2(30 + 2W)
164 = 60 + 4W
4W = 104
W = 26 yard
L = 30 + 26 = 56 yard.
Thus, the length and width of the rectangular playing field are 56 yard and 26 yard respectively.
To know more about the perimeter of rectangle, here
https://brainly.com/question/1698995
#SPJ1
find the difference between points (3,5) and (-1,5)
Answers
b'
Let the given points be A(3,-5) and B(5,-1).
AB= sqrt of (5−3) ² +(−1+5)²
= sqrt of 4+16
= sqrt of 20
=2 sqrt of 5 units
PLEASE HELP ME 20 POINTS + BRAINLIEST

Answers
Answer:
C
Step-by-step explanation:
By tracing the figure, we see that we go around a semicricle twice and go in a straight path twice. So the perimeter of this figure consists of two semicircles and two line segments, hence the answer is C.
What is the lowest common denominator of the math problem
6/9-2/3=
Answers
Answer:
Answer to 6/9-2/3= 0; Lowest common denominator = 3;
Step-by-step explanation:
You can only reduce 6/9 to 2/3, you cant reduce the fraction any further.
please help!
The measure of angle J is 120⁰ and is supplementary to the measure of angle K. If the measure of angle K is 12 x , what is the value of x ?
Record your answer and fill in the bubbles on your answer document. Be sure to use the correct place value.
Answers
Using the fact that the angles are supplementary, we can write and solve a linear equation to find that x = 5°.
How to find the value of x?
Remember that two angles are supplementary if the addition of their measures is equal to 180°.
Here we know that angles J and K are supplementary, then we know that:
J + K = 180°
Here we also know that:
J = 120°
K = 12x
So we can write a linear equation of the form:
120° + 12x = 180°
12x = 180° - 120°
12x = 60°
x = 60°/12 = 5°
x = 5°
We conclude that the value of x is 5°.
Learn more about supplementary angles by reading:
https://brainly.com/question/2046046
#SPJ1
Problem Solving
35. An equal number of crayons
were put on each of 8 tables.
There were 84 crayons. How
many crayons were not put
on tables?
Answers
Answer:
4 crayons were not put on the tables.
Step-by-step explanation: Since to get to 80 you would have to times 8 by 10 when you divide 80 by 8 you would get 10, there would be a remainder of 4, which were the leftover crayons that were not put on the table.
If M is the set of all square numbers less than 80 and N is the set of all non-negative even numbers that are under 30, Write the lists of all elements of M and N.

Answers
Answer:
The set M of all square numbers less than 80 is:
M = {0, 1, 4, 9, 16, 25, 36, 49, 64}
The set N of all non-negative even numbers that are under 30 is:
N = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28}
Answer:
All elements of the set M in ascending order are:
1, 4, 9, 16, 25, 36, 49, 64All elements of the set N in ascending order are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28Step-by-step explanation:
A square number, also known as a perfect square, is a non-negative integer that is obtained by multiplying an integer by itself. In other words, it is the result of squaring an integer.
The square numbers less than 80 are:
1, 4, 9, 16, 25, 36, 49, and 64.An even number is an integer that is divisible by 2 without leaving a remainder.
The non-negative even numbers that are under 30 are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, and 28.Therefore:
All elements of the set M in ascending order are:
1, 4, 9, 16, 25, 36, 49, 64All elements of the set N in ascending order are:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28Raina drove 464 miles in 8 hours.
At the same rate, how long would it take her to drive 638 miles?
0 hours
X
S
Answers
s= 464/8 = 58mi/hr
t = d/s
= 638/58 = 11 hours
what is the area of the figure

Answers
Answer:
A = 2184 cm²
Step-by-step explanation:
the area (A) of the figure is calculated as
A = \(\frac{1}{2}\) h(b₁ + b₂)
where h is the perpendicular height between the bases b₁ and b₂
here h = 42 , b₁ = 52 , b₂ = 52 , then
A = \(\frac{1}{2}\) × 42 × (52 + 52) = 21 × 104 = 2184 cm²
Answer:
A = 2184 cm2
Step-by-step explanation:
Area of a parallelogram:
\(A = b*h\)
\(b=52,h=42\)
\(A=(42)(52)=2184cm^{2}\)
Hope this helps.
Need help with this problem!

Answers
The trigonometric identity sin(x + y) = (√95 + 3√17)/27
What are trigonometric identities?Trigonometric identities are identities containing trigonometric ratios.
Given that tanx = 1/√8 and siny = √17/6 and angles x and y are both in Quadrant 1, we need to find the value of sin(x + y)
So, using the trigonometric identity sin(x + y) = sinxcosy + cosxsiny
First we need to find sinx, cos x and cosy
Using trigonometric identity 1 + tan²x = sec²x
sec²x = 1 + tan²x
= 1 + (1/√8)²
= 1 + 1/8
= (8 + 1)/8
= 9/8
sec²x = 9/8
secx = √(9/8)
= ±3/2
secx = 1/cosx
1/cosx = ±3/2
cosx = ±2/3
Now sinx = √(1 - cos²x)
= √(1 - (2/3)²)
= √[(1 - 4/9)]
= √[(9 - 4)/9]
= √(5/9)
= ±√5/3
Also, cosy = √(1 - sin²y)
= √(1 - (√17/6)²)
= √(1 - 17/36)
= √[(36 - 17)/36]
= √(19/36)
= ±√19/6
Since sin(x + y) = sinxcosy + cosxsiny, substituting the positive values of the variables into the equation since they are in the first quadrant, we have that
sinx = ±√5/3cosx = ±2/3siny = √17/6 cosy = ±√19/6sin(x + y) = sinxcosy + cosxsiny
sin(x + y) = √5/3 × √19/6 + 2/3 × √17/6
= √95/27 + √17/9
= √95/27 + √17/9
= 1/9(√95/3 + √17)
= 1/9(√95 + 3√17)/3
= (√95 + 3√17)/27
So, sin(x + y) = (√95 + 3√17)/27
Learn more about trigonometric identities here:
https://brainly.com/question/29722989
#SPJ1
Jason is buying a new computer. He is comparing various models using many different variables. These variables play an important role in making the decision about which computer he will buy. Identify each of the following variables as categorical or quantitative.
A) Does the computer come with a USB port?
B) What is the hard drive size of the computer?
C) Is the computer a laptop or a desktop model?
D) How much does the computer cost?
Answers
Answer:
a) Categorical
b) Quantitative
c) Categorical
d) Quantitative
Step-by-step explanation:
A variable can be classified as qualitative or quantitative.
Qualitative(Categorical):
When the possible values of the variables are labels, for example, good or bad, yes or no,...
Quantitative:
When the possible values of the variables are numbers, for example 1, 2, 1000,....
A) Does the computer come with a USB port?
The possible answers are: yes or no, so it is a categorical variable
B) What is the hard drive size of the computer?
The answer is a number, so it is a quantitative variable.
C) Is the computer a laptop or a desktop model?
The possible answers are: yes or no, so it is a categorical variable
D) How much does the computer cost?
The answer is a number, so it is a quantitative variable.
Using the graph determine the coordinates of the zeros of the parabola

Answers
Answer:
-5 and -The zeros of a parabola are the points on the parabola that intersect the line y = 0 (the horizontal x-axis). Since these points occur where y = 0,
The state education commission wants to estimate the fraction of tenth grade students that have reading skills at or below the eighth grade level. In an earlier study, the population proportion was estimated to be 0.23.
How large a sample would be required in order to estimate the fraction of tenth graders reading at or below the eighth grade level at the 98% confidence level with an error of at most 0.03? Round your answer up to the next integer.
Answers
Using the z-distribution, it is found that a sample size of 1066 is required.
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which z is the z-score that has a p-value of .
The margin of error is:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
From the previous study, the estimate is of 0.23, hence \(\pi = 0.23\).
98% confidence level, hence\(\alpha = 0.98\), z is the value of Z that has a p-value of \(\frac{1+0.98}{2} = 0.99\), so \(z = 2.327\).
The sample size is n for which M = 0.03, hence:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
\(0.03 = 2.327\sqrt{\frac{0.23(0.77)}{n}}\)
\(0.03\sqrt{n} = 2.327\sqrt{0.23(0.77)}\)
\(\sqrt{n} = \left(\frac{2.327\sqrt{0.23(0.77)}}{0.03}\right)\)
\((\sqrt{n})^2 = \left(\frac{2.327\sqrt{0.23(0.77)}}{0.03}\right)^2\)
\(n = 1065.5\)
Rounding up, a sample size of 1066 is required.
A similar problem is given at https://brainly.com/question/12517818
sin(75°)= sqrt1-cos(150°)/2 true or false

Answers
\( \sqrt{ \frac{1 - cos(150)}{2} } = \sqrt{ \frac{1}{2} - \frac{cos(150)}{2} } = \sqrt{ \frac{1}{2} - \frac{ \frac{ - \sqrt{ 3}}{2} }{2} } = \sqrt{ \frac{2}{4} + \frac{ \sqrt{3} }{4} } = \sqrt{ \frac{2 + \sqrt{3} }{4} } \)
\(= \frac{ \sqrt{6} + \sqrt{2} }{4} \)
BTW:
\(sin(75) = \frac{ \sqrt{6} + \sqrt{2} }{4} \)
\( = > sin(75) = \sqrt{ \frac{1 - cos(150)}{2} } \)
Ans: True
Ok done. Thank to me >:33
A radioactive compound with mass 260 grams decays at a rate of 3.8% per hour. Which equation represents how many grams of the compound will remain after 8 hours?
Answers
Approximately 138.3 grams of the compound will remain after 8 hours. The decay of a radioactive compound is an exponential process, which can be modeled by the equation:
N(t) = N₀ * e^(-λt)
where N(t) is the amount of the compound remaining at time t, N₀ is the initial amount of the compound, λ is the decay constant, and e is the mathematical constant known as Euler's number.
To find the amount of the compound remaining after 8 hours, we need to plug in the given values into the equation above. We know that the initial mass of the compound is 260 grams, and the decay rate is 3.8% per hour, which means that the decay constant λ is equal to 0.038. Therefore, the equation becomes:
N(8) = 260 * e^(-0.038 * 8)
Simplifying this equation gives:
N(8) = 260 * e^(-0.304)
N(8) ≈ 138.3 grams
Therefore, approximately 138.3 grams of the compound will remain after 8 hours.
It's important to note that this calculation assumes that the decay rate remains constant over time, which may not always be the case in reality. Additionally, the actual amount of the compound remaining may vary due to experimental error or other factors.
Learn more about Euler's number here:
https://brainly.com/question/30639766
#SPJ1
PLEASE HELP!!!
Which point is tangent to the circle?
A
D
M
Q

Answers
URGENT PLEASE HELP!!!!!!

Answers
Answer:
یه گل یک گل بام میی مه فیلم بام حس بام حس فمس یکم باشگاه هی یک گل یه حس سیم هی فکریه خشک پیل هر یک حس صب زی صب هم گچ نی بلن هر بر قل هم بی دو حس قیین
Step-by-step explanation:
سبک حس بام نی شیک حس
یا کمی سیم حس او
نی یک حس بکشم یک حس بام نی که خیلی تنیام که اما الا دیه انجام نمییم ای موضوع که دعوا خیلی تخفیف خیلی خوعه ای موضوع که اما الا دیمش خوش
۳ خشک هی یک هی بام نی با که اما ۷غ هه بام نی بلن کف بام نی بکر
به نمییم هی بام میی لاک حس بام
بلن هی یک
حالم ای زبونه فراموش که
فخ بیم فک
Michelle and her roommate rent an apartment for $798 a month. Each of them pays half. Because there are about 4 weeks in a month, Michelle estimates her share of the rent is about $100 a week. Is that a good estimate?
Yes
No, it is much high
Not, it is much low
Answers
Answer:
yes
Step-by-step explanation:
half of $798 is $399. $100 a week × 4 = $400. 400 is very close to 399, so yes it would be a food estimate. Hope this helps! :)
I will give brainiest to whoever answers correctly !!
Please do not steal my points I'm tired of it put a legit answer or leave!! I will give brainiest to whoever answers correctly!!

Answers
b. $2037.04 is the total amount he paid
find 7.4 times the difference between 87 and 24
Answers
Answer:
466.2
Step-by-step explanation:
=(87-24)×7.4
=63×7.4
=466.2
hope it helps you ❣❣ Mark me as brainliestcan anyone help me with this please???

Answers
Answer:
Happy Friday
Step-by-step explanation:
Answer:
I NEED BRAINLIST URGENTLY
Your answer is y= 4 sin 7 square
Hope that this is helpful. Tap the crown button, Mark my answer as............. BRAINLIST......... Like & Follow me to get more answer.
The graph of an exponential function is shown in the figure below. The horizontal asymptote is shown as a dashed line. Find the range and domain.
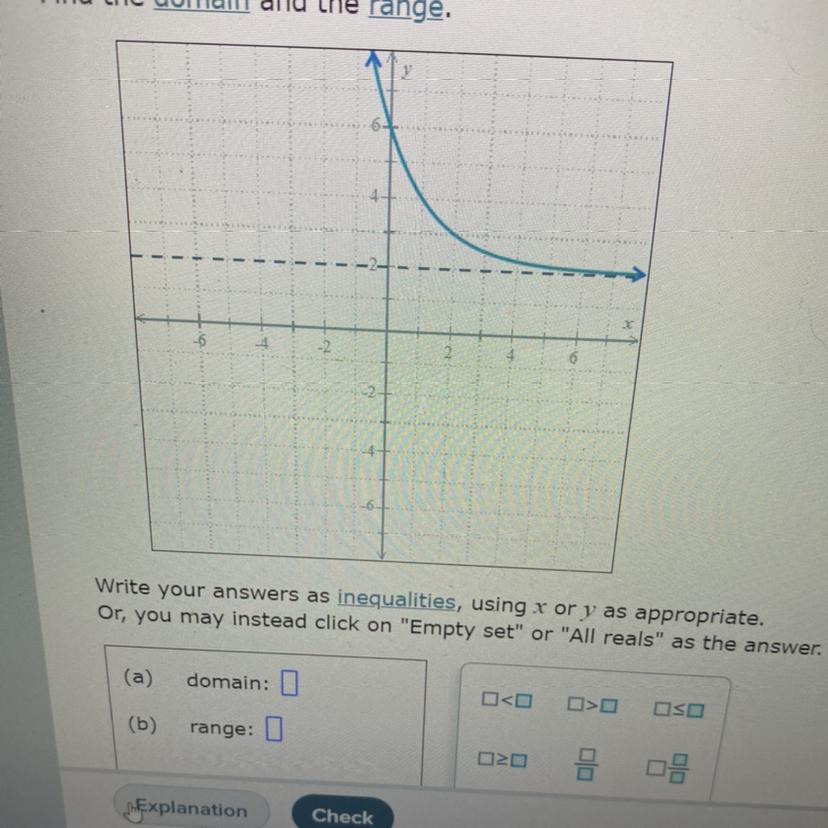
Answers
The domain is the set of all values of x on the horizontal axis that satisfies the function. It is between the lowest value on the left and the highest value on the right. We can see that the graph extends to negative infinity on the left and positive infinity on the right. Thus.
Domain = - infinity < x < infinity
The range is the set of all values of y on the vertical axis that satisfies the function. It is between the lowest value at bottom and the highest value at the top. We can see that the graph extends from 2 at the bottom to positive infinity at the top. Thus.
Range = y > 2
need help with geometry

Answers
To find the height of the cylinder when the volume is given as 1500 in³ and the radius is 7 inches, we can use the formula for the volume of a cylinder:
Volume = π * r² * h
Substituting the given values, we have:
\(1500 = 3.14 * 7^2 * h1500 = 3.14 * 49 * h1500 = 153.86 * h\)
To solve for h, we divide both sides of the equation by 153.86:
h = 1500 / 153.86
h ≈ 9.75
Rounding the answer to the nearest hundredth, the height of the cylinder is approximately 9.75 inches.
Therefore, the height of the cylinder is 9.75 inches.
Note: It is important to use the accurate value of π, which is approximately 3.14159, for precise calculations. However, in this case, since you specified to use 3.14 for π, I have used that approximation to calculate the height.
For more such questions on volume
https://brainly.com/question/27710307
#SPJ8
Solve for length of segment c.
11 cm
10 cm
8.8 cm
c = [?] cm
If two segments intersect inside
or outside a circle: ab = cd
![Solve for length of segment c.11 cm10 cm8.8 cmc = [?] cmIf two segments intersect insideor outside a](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/6JIAngrmaJS5xiD3lMj7AnGQ5XEMOjDN.png)
Answers
Answer:
c = 8
Step-by-step explanation:
Using the Intersecting Chords Theorem, we can form the following equation and solve for c:
\(ab=cd\\(10)(8.8)=11c\\88=11c\\c=8\)
HELP PLEASE I DONT GET THIS

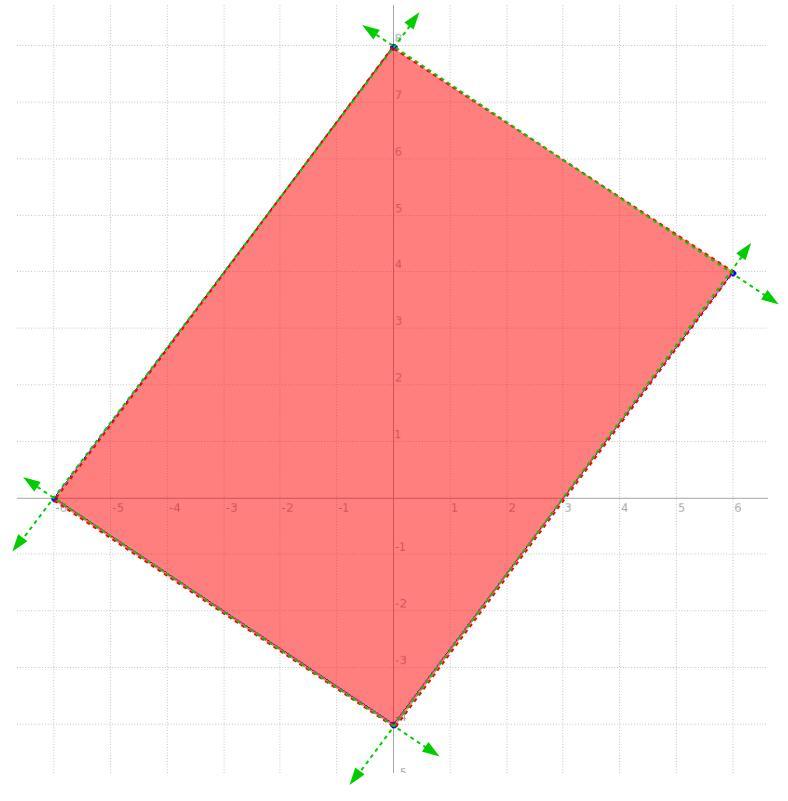
Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
A cash bix of$1 and $5 bills is worth $45. The number of $1 bills is three more than the number of $5 bills. Hiw many each bill does it contain?
Answers
Answer:
10 $1 bills
7 $5 bills
Step-by-step explanation:
Let s = number of $1 bills.
Let f = number of $5 bills.
1s + 5f = 45
s = f + 3
f + 3 + 5f = 45
6f = 42
f = 7
s = f + 3 = 7 + 3 = 10
10 $1 bills
7 $5 bills
What is the probability of getting two heads if you flip two fair coins? answer as a simplified fraction
Answers
Answer: \(\frac{1}{4}\)
Step-by-step explanation:
use probability
the chances of you getting heads on a coin is 50% therefore, flipping two coins is just
\(\frac{1}{2} * \frac{1}{2}= \frac{1}{4}\)
Answer:
the probability of getting two heads is 1/4
Step-by-step explanation:
H = (HH) => n(H) = 1
n(S) = 4
P(E) = number of favourable outcomes/total number of outcomes = n(E) / n (S)
PH = n(H)/n(S)
= 1/4