Dennis and Connie purchased a radio for $128. Dennis paid $36 more than Connie. How much did each pay?
Answers
Answer:
Dennis paid $82 and Connie paid $46.
Step-by-step explanation:
We can set up an equation by putting in variables, c representing how much Connie paid. Since we know that Dennis paid $36 more, we will also factor that in the equation.
c + c + 36 = 128
Where c + 36 represents the amount Dennis paid, and 128 represents the total amount paid as given in the question. We can start by adding like terms. 2c + 36 = 128
Now, we can subtract 36 from each side,
2c + 36 - 36 = 128 - 36
2c = 92
Divide each side by two,
2c/2 = 92/2
c = 46
Now, to make sure this is correct, let's substitute our c for 46 in our equation:
46 + 46 + 36 = 128
92 + 36 = 128
128 = 128
Therefore, our equation is correct, and Dennis paid $82 while Connie paid $46.
Related Questions
f(x) = (x - 1)²
Helpppp!

Answers
Answer:
x = 1
Step-by-step explanation:
f(x) = (x - 1)²
f(x) = (x -1)(x - 1)
*Note: to find zeros set your equation equal to zero
x - 1 = 0
x = 1
*Since both quantities are the same x = 1 is your only zero.
translate each of the following multiplicative expressions into its additive counterpart. assume that the operation is commutative. a. a2b3 b. a22(b21c)2 c. (ab2)23c2 5 e
Answers
The additive counterpart of given expressions are (2a+3b), -2a+2(-b+c), and -3(a+2b)+2c=0.
When two numbers may be added together or multiplied, regardless of the order in which they are entered, the result is said to be commutative. There are different formulas available for the conversion of multiplicative expressions to their additive counterparts.
a) The first expression is a²b³. This expression is written as aabbb. This is of the form ab and its corresponding additive counterpart is of the form a+b.
Then, a+a+b+b+b=2a+3b.
b) The second expression is a⁻²(b⁻¹c)². This expression is of the form a⁻¹ and its corresponding additive counterpart is of the form -a.
Then,
\(\begin{aligned}a^{-2}(b^{-1}c)^2&=a^{-1}a^{-1}(b^{-1}c)(b^{-1}c)\\&=-a-a-b+c-b+c\\&=-2a+2(-b+c)\end{aligned}\)
c) The third expression is (ab²)⁻³c²=e. This expression is first expanded as, (ab²)⁻¹(ab²)⁻¹(ab²)⁻¹c²=e. Using property, (xy)⁻¹=y⁻¹x⁻¹.
Then,
\(\begin{aligned}((b^2)^{-1}a^{-1})((b^2)^{-1}a^{-1})((b^2)^{-1}a^{-1})c^2&=e\\(b^{-2}a^{-1})(b^{-2}a^{-1})(b^{-2}a^{-1})c^2&=e\end{aligned}\)
Also, the additive identity to e is zero. And, aⁿ=na.
Then,
(-2b-a)+(-2b-a)+(-2b-a)+2c=0
Simplifying we get,
-3(a+2b)+2c=0.
The answers are (2a+3b), -2a+2(-b+c), and -3(a+2b)+2c=0.
The complete question is -
Translate each of the following multiplicative expressions into its additive counterpart. assume that the operation is commutative
a. a²b³
b. a⁻²(b⁻¹c)²
c. (ab²)⁻³c²=e
To know more about commutative:
https://brainly.com/question/778086
#SPJ4
An airplane traveled 108 miles in 20 minutes? How long will it take to fly 162 miles?
a
30 min
b
25 min
c
8.1min
d
35 min
omg pls help me im giving like all my points out for this
Answers
Answer:
poopy
Step-by-step explanation:
Tee Hee
Answer:
a, 30 minutes
Step-by-step explanation:
108 divided by 20 is 54
162 divided by 54 is 30
Solve each equation. Check each solution. 2/n + n+2 / n+1 = -2 / n² + n
Answers
The solution of given rational equation \(\frac{2}{n} +\frac{n+2}{n+1}=\frac{-2}{n^2+n}\) is n = -2
In this question,
We have been given a rational equation.
\(\frac{2}{n} +\frac{n+2}{n+1}=\frac{-2}{n^2+n}\)
We need to find the solution of given rational equation.
First we simplify the LHS of given equation.
\(\frac{2}{n} +\frac{n+2}{n+1}\\\\=\frac{2(n+1)+n(n+2)}{n(n+1)} \\\\=\frac{2n+2+n^2+2n}{n^2+n}\\\\ =\frac{n^2+4n+2}{n^2+n}\)
So, given equation would be,
\(\frac{n^2+4n+2}{n^2+n}=\frac{-2}{n^2+n}\)
Here, the denominator is same on the both sides.
⇒ n² + 4n + 2 = -2
⇒ n² + 4n + 4 = 0
⇒ (n + 2)² = 0
⇒ n + 2 = 0
⇒ n = -2
We need to check above solution.
so, substitute n = -2 in LHS of given equation.
\(\frac{2}{-2} +\frac{-2+2}{-2+1}\\\\=-1+0\\\\=-1\)
Now, substitute n = -2 in RHS of given equation.
\(\frac{-2}{-2^2-2}\\\\=\frac{-2}{4-2}\\\\= \frac{-2}{2} \\\\-1\)
For n = -2, LHS = RHS
Therefore, the solution of given rational equation \(\frac{2}{n} +\frac{n+2}{n+1}=\frac{-2}{n^2+n}\) is n = -2
Learn more about the rational equation here:
brainly.com/question/20850120
#SPJ4
how do you find a decimal in a equation.
Answers
Step-by-step explanation:
if it's a percent move place's to the left to times and add our decimaldecimal point
Answer:
You can find a decimal when you see a number with a dot in it
example:5.56 is counted as a decimal
Expand the binomial using the binomial theorem: (3x-4)^5
Can someone explain how you solve this?
Answers
Answer:
Step-by-step explanation:
We worry about 2 things:
-terms power
-coefficient for each term
(3x-4)^5, has 2 terms 3x and -4
-Start with the first term to the highest power 5 and second term to the lowest power 0, then the high power goes down and low power increases until the first term has the lowest power 0 and the second term has the highest power 5.
-The coefficients for each term we take it from the Pascal triangle.
For the the power 5 the coefficients are 1, 5, 10, 10, 5, 1
\((3x-4)^{5} = 1*(3x)^{5} *(-4)^{0} +5*(3x)^{4} *(-4)^{1} +10*(3x)^{3} *(-4)^{2}+10*(3x)^{2} *(-4)^{3}+5*(3x)^{1} *(-4)^{4}+1*(3x)^{0} *(-4)^{5}\)
Simplify:
\((3x-4)^{5} = 3^{5} x^{5} -20*3^{4} x^{4} +160*3^{3} x^{3}-640*3^{2} x^{2}+1280*3x-1024\)
\((3x-4)^{5} = 243 x^{5} -1,620x^{4} +4,320 x^{3}-5,760x^{2}+3,840x-1024\)
Given: abcd is a rectangle, M is midpoint of line AB prove: line DM is congruent to CM
Answers
DM is congruent to line CM because CDM is congruent to triangle CBM using the SAS congruence criteria for triangles.
Draw a diagram of the rectangle ABCD with M as the midpoint of AB. Draw lines CM and DM ( refer to the attached image). Since AB is a line segment, we know that AM is congruent to MB (because M is the midpoint of AB). Since ABCD is a rectangle, we know that AB is parallel to CD, and AD is parallel to BC. Thus, we have two pairs of parallel lines: AB and CD, and AD and BC.
Using the fact that opposite sides of a rectangle are congruent, we have CD = AB. Now, we have a pair of congruent sides (DM and CM) that are opposite each other in triangle CDM and CBM respectively. We also have another pair of congruent sides (CD and AB) that are opposite each other in both triangles. Finally, we know that the angle CMD is congruent to the angle CMB because they are vertical angles. By the Side-Angle-Side (SAS) congruence criterion, we can conclude that triangle CDM is congruent to triangle CBM.
Therefore, line DM is congruent to line CM by SAS congruence criteria.
To learn more about congruence, refer to:
https://brainly.com/question/30094441
#SPJ4

a package of 9 batteries cost $4.72 what is the cost per battery
Answers
Answer: 1.90
Step-by-step explanation:
9/4.72= 1.90
Answer:
1.90
Step-by-step explanation:
9/4.72= 1.90
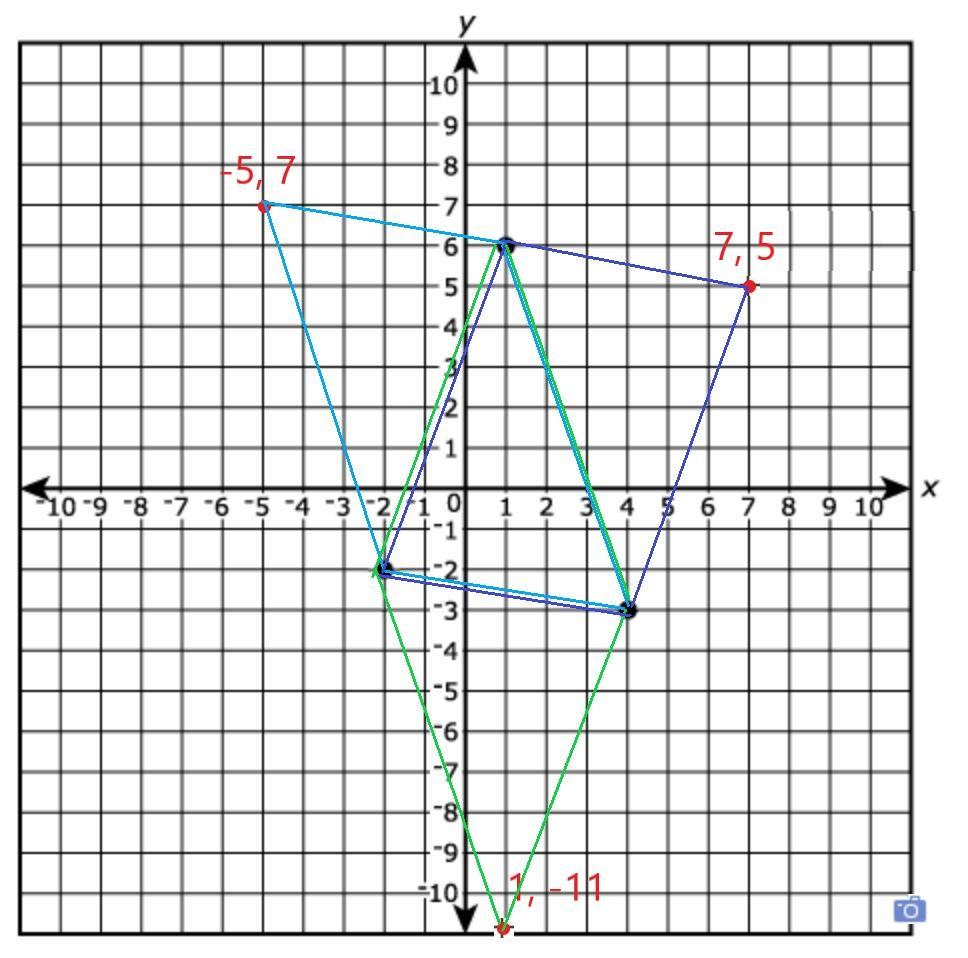
Three points are graphed on the coordinate plane. Dave must find a fourth point so that the four points will form a parallelogram. Find all 3 possibilities for the fourth point. Drag and drop the numbers into the ordered pairs. I'm so so confused. Can somebody please please help? I put the drag and drop numbers as the second picture.


Answers
Answer:
(-5, 7), (7, 5) and (1, -11)
Step-by-step explanation:
see attached for points and possible parallelograms, they distinguished by different colored lines
the 3 points are: (-5, 7), (7, 5) and (1, -11)
prove that d dx (csc(x)) = −csc(x) cot(x).
Answers
according to question we have proved that d/dx(csc(x)) = -csc(x) * cot(x).
To prove that d/dx (csc(x)) = -csc(x) cot(x), we can use the quotient rule and the identity csc(x) = 1/sin(x):
d/dx(csc(x)) = d/dx(1/sin(x))
Using the quotient rule, we have:
d/dx(1/sin(x)) = (-1/sin^2(x)) * d/dx(sin(x))
Using the chain rule, we have:
d/dx(sin(x)) = cos(x)
Substituting this back in, we get:
d/dx(csc(x)) = (-1/sin^2(x)) * cos(x)
Using the identity cos(x) = cos(x) * (1/sin(x)) * sin(x), we can rewrite the expression as:
d/dx(csc(x)) = (-1/sin^2(x)) * cos(x) * (1/sin(x)) * sin(x)
Simplifying this gives:
d/dx(csc(x)) = (-cos(x)/sin^2(x)) * (1/sin(x))
Using the identity cot(x) = cos(x)/sin(x), we can write this as:
d/dx(csc(x)) = (-cot(x)) * (1/sin(x))
Finally, using the identity csc(x) = 1/sin(x), we get:
d/dx(csc(x)) = -csc(x) * cot(x)
To know more about expression visit:
brainly.com/question/28170201
#SPJ11
Which expression is equivalent to -8?

Answers
Answer:
2^-3
Step-by-step explanation:
Answer:
The answer is the second one: \((-1/2)^{-3}\)
Step-by-step explanation:
1) When an exponent is negative, we must 'flip' the term before applying the exponent.
\((-1/2)^{-3}\) = \((-2/1)^3\)= \(-2^3\)
2) Next, we need to cube two. Remember, the negative number does not apply yet!
\(-2^3\) = -8
3) Thus, we get our answer. -8.
I hope this help, firend!!
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases. *
Answers
On solving the provided question, we can say that the spherical balloon's initial radius is 7 cm.; the final radius is 14 cm. ratio = (7/14) ^2 = 1:4
what is radius?The length of a circle or sphere, in more contemporary use, is the same as its radius in classical geometry, which is one of the line segments from its center to its circumference. The Latin word radius, which also refers to the spokes of a wagon wheel, gave rise to the term. The distance a circle's center is from any point on its perimeter is its radius. Usually, "R" or "r" is used to indicate it. A radius is a line segment that has one endpoint in the center and one on the circumference of a circle. Circular diameter equals radius The diameter of a circle is the segment that traverses its center and has ends that are on the circle.
The spherical balloon's initial radius is 7 cm.
The final radius is 14 cm.
ratio =
(7/14) ^2 = 1:4
To know more about radius visit:
https://brainly.com/question/28946570
#SPJ4
subtract (-10ab + 7a² - b²) from (8b² + ab - 2a²)
Answers
not sure if this is right, did the math in my head but if you wanna check the math yourself you have to do the first equation plus the negative version of the second equation
Figure ABCD is a trapezoid.
Find the value of x.

Answers
Answer:?
Step-by-step explanation:
Which line is perpendicular to a line that has a slope of -5/6?

Answers
Answer:
P
Step-by-step explanation:
Find the largest open interval where the function is changing as requested decreasing; f(x)=x^3-4x
Answers
The largest open interval where f(x) is decreasing is (-2√(1/3), 2√(1/3)). In interval notation, this can be written as (-2√(1/3), 2√(1/3)).
To determine where the function f(x) = x^3 - 4x is decreasing, we need to find the intervals where the derivative is negative. Let's calculate the derivative of f(x) first:
f'(x) = 3x² - 4
To find where f'(x) < 0, let's solve the inequality:
3x² - 4 < 0
Adding 4 to both sides gives:
3x² < 4
Dividing both sides by 3 gives:
x² < 4/3
Taking the square root of both sides (and considering both the positive and negative square root) gives:
x < √(4/3) and x > -√(4/3)
Simplifying further, we have:
x < 2√(1/3) and x > -2√(1/3)
The largest open interval where f(x) is decreasing is (-2√(1/3), 2√(1/3)). In interval notation, this can be written as (-2√(1/3), 2√(1/3)).
To know more about interval notation;
https://brainly.com/question/13048073
We need to investigate the behavior of the derivative of the feature. If the spinoff is negative inside a c program language period, then the quality is lowering over that c language.
Let's begin by finding the derivative of the function f(x) = x^3 - 4x:
f'(x) = 3x^2 - 4
we set f'(x) < zero:
3x^2 - four < zero.
Now, permit's remedy this inequality:
3x^2 < 4,
x^2 < four/three,
x^2 - 4/three < 0.
To find the critical points, we set x^2 - 4/three = zero:
x^2 = 4/three,
x = ±√(4/three),
x = ±2/√3.
We need to test the durations among the essential factors and beyond.
For x < -2/√3, allow's select x = -1. Plugging this cost into f'(x):
'(-1) = three(-1)^2 - four = -1.
Since f'(-1) < zero, the characteristic is decreasing for x < -2/√3.
For -2/√three < x < 2/√three, permits select x = zero. Plugging this price into f'(x):
f'(0) = 3(0)^2 - four = -four.
Since f'(0) < zero, the characteristic is lowering for -2/√three < x < 2/√3.
For x > 2/√three, permits choose x = 1. Plugging this cost into f'(x):
f'(1) = three(1)^2 - four = -1.
Since f'(1) < 0, the function is decreasing for x > 2/√3.
Therefore, the largest open c language in which the characteristic f(x) = x^3 - 4x is lowering is (-∞, 2/√three).
(sinA + cosA)/ (secA + cosecA) = sinA* cosA
Answers
Answer:
Proof below
Step-by-step explanation:
Trigonometric Identities
We'll prove that:
\(\displaystyle \frac{\sin A+\cos A}{\sec A+\csc A}=\sin A*\cos A\)
Recall:
\(\displaystyle \sec A =\frac{1}{\cos A}\)
\(\displaystyle \csc A =\frac{1}{\sin A}\)
Applying those definitions:
\(\displaystyle \frac{\sin A+\cos A}{\sec A+\csc A}=\frac{\sin A+\cos A}{\frac{1}{\cos A}+\frac{1}{\sin A}}\)
Adding the fractions:
\(\displaystyle \frac{\sin A+\cos A}{\sec A+\csc A}=\frac{\sin A+\cos A}{\frac{\sin A+\cos A}{\cos A*\sin A}}\)
Dividing the fractions:
\(\displaystyle \frac{\sin A+\cos A}{\sec A+\csc A}=(\sin A+\cos A)*\frac{\cos A*\sin A}{\sin A+\cos A}\)
Simplifying:
\(\displaystyle \frac{\sin A+\cos A}{\sec A+\csc A}=\cos A*\sin A\)
Hence proved
i need help on this equation please.

Answers
9514 1404 393
Answer:
2.43 m
Step-by-step explanation:
The wavelength is the distance between crests, given as 2.43 m.
LowStress Marketing Research designed a perceptual mapping study to compare several leading brands of soap for Bubbles O'Connor, product manager for Slippery Soap. Bubbles asked to see a sample question from the study and was shown the following format: Slipery Soap is a disinfectant soap: Neither Agree or Disagree, 4) Disagree, 5) Strongly Disagree. In addition, Bubbles saw the results from the regression analysis for soaps in the study which showed the following equation: Overall Preference -2.1 +2.3* Cleaning Ability+1.0* Cost+0.6 Disinfecting Ability. What would be the slope of the ideal vector?
Answers
The slope of the ideal vector, determined by examining the coefficients of the variables in the regression equation is:
Cleaning Ability: 2.3
Cost: 1.0
Disinfecting Ability: 0.6.
In this case, the regression equation is:
Overall Preference = -2.1 + 2.3 * Cleaning Ability + 1.0 * Cost + 0.6 * Disinfecting Ability
The coefficients of the variables represent the weights or importance assigned to each variable in determining the overall preference. Therefore, the slope of the ideal vector would be the coefficients of the variables in the regression equation.
Based on the given regression equation, the slope of the ideal vector would be:
Cleaning Ability: 2.3
Cost: 1.0
Disinfecting Ability: 0.6
These values indicate the relative importance or impact of each variable on the overall preference for Slippery Soap.
Learn more about regression equation here:
https://brainly.com/question/32810839
#SPJ11
Helen determined she walks about 1,800 steps per 5 of a mile. How many steps did she take if she walked 5 miles?
Answers
Answer: Most likely 6,750 steps
Samir recorded the number of different types of pets his friends have in the table shown below:
Cats 2
Dogs 4
Rabbits 1
Guinea Pigs 4
Which of the following plots represents the data in the table?




Answers
I need this answer asap!! Taylor earned $338.00 at her job when she worked for 20 hours. What was her hourly wage, in dollars per hour?
Answers
Answer:
$16.90 per hour
Step-by-step explanation:
You want the hourly wage Taylor earned when she worked 20 hours for $338.00.
Hourly wageTo find dollars per hour, divide dollars by hours:
$338.00/(20 h) = $16.90/h
Taylor earned $16.90 per hour.
<95141404393>

The ph measurements of water specimens from various locations along a given river basin are Normally distributed with mean 8 and standard deviation 0. 3. What is approximately, the probability that the pH measurements of a randomly selected water specimen is value between 7. 5 and 8. 2
Answers
The probability that a randomly selected water specimen has a pH value between 7.5 and 8.2 is approximately 0.6287. We can calculate it in the following manner.
We are given that pH measurements of water specimens from various locations along a river basin are normally distributed with a mean of 8 and a standard deviation of 0.3. We want to find the probability that a randomly selected water specimen has a pH value between 7.5 and 8.2.
To solve this problem, we can standardize the pH values using the standard normal distribution, which has a mean of 0 and a standard deviation of 1.
First, we find the z-scores for pH values of 7.5 and 8.2 as follows:
z1 = (7.5 - 8) / 0.3 = -1.67
z2 = (8.2 - 8) / 0.3 = 0.67
Next, we use a standard normal distribution table or calculator to find the area under the curve between these two z-scores:
P(-1.67 < Z < 0.67)
Using a standard normal distribution table or calculator, we find that the area under the curve between -1.67 and 0.67 is approximately 0.6287.
Therefore, the probability that a randomly selected water specimen has a pH value between 7.5 and 8.2 is approximately 0.6287.
Learn more about mean here brainly.com/question/31101410
#SPJ4
reflect across the y axis

Answers
Answer:
See below
Step-by-step explanation:
Plot these points and that will be the reflection:
S is going to equal (3,1)
R is going to equal (-3,3)
T is going to equal (-1,-5)
Q is going to equal (-4,-2)
Let me know if you need help plotting points too.
-5(6+x). Use the distributive property to evaluate each expression.
Answers
Answer:
-5x-30
I'm kinda tired rn so I just multiplied 5 with everything in the ()
2) −4 + n/3= −4 solve the equation
Answers
Answer: n=−6
Step-by-step explanation: Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
2-4+n/3-(-4)=0
simplify n/3
(-2+n/3)- -4=0
Rewrite the whole as a fraction using 3 as the denominator :
-2 • 3
-2 = -2/1 = -2X3/3
Equivalent fraction : The fraction thus generated looks different but has the same value as the whole
Common denominator : The equivalent fraction and the other fraction involved in the calculation share the same denominator
-2 • 3 + n /3=n-6/3
n+6 = 0
Subtract 6 from both sides of the equation :
n = -6
A lattice point is an ordered pair (x, y) where both x and y are integers. A triangle is formed
by the three points (1, 1), (9, 1), and (9, n). For what integer value of n > 0 are there exactly 560 lattice
points strictly in the interior of the triangle?
Answers
To find the integer value of n that results in exactly 560 lattice points strictly in the interior of the triangle, use the equation: n = (560 + 2)/8.
This equation is derived by counting the lattice points on each side of the triangle, starting with the side between points (1,1) and (9,1). This side has a length of 8, so it contains 8 lattice points, including the two endpoints. The remaining sides have lengths of 8 + n and 8 + n, which combined have 8 + 2n lattice points. The total number of lattice points in the triangle is then 8 + 8 + 2n = 16 + 2n.
Solving for n when the total number of lattice points is 560 gives us n = (560 + 2)/8. Therefore, the integer value of n is 70.
To learn more about this visit - A lattice point is an ordered pair (x, y) : https://brainly.com/question/22421833
#SPJ11
5(x + 4) + 3(x + 2) Expanded and simplified
Answers
5(x+4) + 3(x + 2)
5x + 5 x 4 + 3x + 3 x 2
5x + 20 + 3x + 6
* 8x + 6 *
Answer:
\(\mathrm{8x+26}\)Step-by-step explanation:
\(\mathrm{5(x + 4) + 3(x + 2)}\)
Expand:-
\(\mathrm{5x+20+3x+6}\)
Combine like terms:-
\(\mathrm{5x+3x+20+6}\)
\(\mathrm{(5x+3x)=\bf 8x}\)
\(\mathrm{(20+6)=\bf 26}\)
\(\mathrm{8x+26}\)
______________________
Hope this helps!
Фd —
969 - 9
ХОТХЭ:
P
Answers
https://brainly.com/question/24478767
Question of 10 Use the grouping method to factor 2 +672 - 7x-21, A. (x+3)(2x - 7) B. (x-3)(2+7) O C. (x - 3)(x + 7) D. 2x+3)(x-7)
