Describe the graph of the line y = -5.

The equation of a line passing through the point (5,-3) and parallel to 6x+3y=-12 is y =-2x+7.

Parallel lines are those that never intersect. As a result, two parallel lines must have the same slope but different intercepts (if they had the same intercepts, they would be identical lines).

The equation of the line is 6x+3y=-12.

6x+3y=-12​

3y =-12-6x

y = -2x-4    

The slope of this line is -2.

Because parallel lines have the same slope, the new line will also have a slope of -2.

You now have a point (5,-3) and a slope; thus, use the Point-Slope form to solve the equation of a line.

y-y₁= m(x-x₁)

y+3 = -2(x -5)

y+3 = -2x+10

y =-2x+7

The equation of a line passing through the point (5,-3) and parallel to 6x+3y=-12 is y =-2x+7.

To know more about equation of parallel lines, visit:

https://brainly.com/question/402319

#SPJ9

Answer:

y= -2/5x + -3

Step-by-step explanation:

y=mx+b

-1= -2/5(-5) +b

-1= 2+b

Solve for b

b= -3

Fill in the b and m and you get the answer

Answer:

Step-by-step explanation:

Let the age of daughter be x

Then the age of father will be x + 28

In 6 years time:-

The age of father = x + 28 + 2 = 30 + x

The age of daughter = x + 6

According to the question,

Father will be three times the age of his daughter.

30 + x = 3(x + 6)

30 + x = 3x + 18

x - 3x = 18 - 30

-2x = - 12

x = - 12/-2

x = 6

So therfore,

Daughter's present age = 6 years

Father's present age = 34 years

Hope this helps :)

Answer:

I need the answer

Step-by-step explanation:

Answer:

Step-by-step explanation:

The sample is the part of the population that somebody wants to study. therefore, the sample is the 100 male students interviewed

Answer: 31 7/8

Step-by-step explanation:

Firstly, we add the whole part which is 31 into the fraction making it an improper fraction. Then solve the problem by making a common denominator of 3/4  from the whole fraction into 6/8 and adding it to the previous fraction, then subtracting the spilled amount. To make the improper fraction a whole fraction/normal, just divide by the denominator. That's all!

31 x 8 = 248

248 + 6 = 254

254 - 7 = 247

247 ÷ 8 = 31 + \(\frac{7}{8}\)

OR 31 \(\frac{7}{8}\)

to divide fractions, flip the second fraction around (take the reciprocal), multiply the fractions, and simplify the answer.

To divide with fractions, you need to multiply the first fraction by the reciprocal of the second fraction. Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction, as you stated. Here is how it works in detail:Step 1: Flip the second fraction. You will need to take the reciprocal of the second fraction, meaning you will flip it around. This way, instead of dividing the fractions, you will be multiplying them.Step 2: Multiply the first fraction by the reciprocal of the second fraction. Next, you will multiply the first fraction by the reciprocal of the second fraction.

You can write this as: \($$\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}$$\)\($$\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}$$\)

Note that this is simply multiplying the first fraction by the flipped second fraction, as you stated earlier. Step 3: Simplify the result. Finally, you will need to simplify the result if possible. You can do this by reducing the fraction to its lowest terms, if necessary. If you're asked to give the answer as a mixed number, you will need to convert the improper fraction to a mixed number. In conclusion, to divide fractions, flip the second fraction around (take the reciprocal), multiply the fractions, and simplify the answer.

To know more about fractions, visit ;-

https://brainly.com/question/10354322

#SPJ11

Answer:

18/4=45

Step-by-step explanation:

\(7x = 35\)

\(x = \frac{35}{7} = 5\)

Sam bought a baseball glove for $35. That is 7 times as much as he paid for a baseball. Therefore, The ball was 5$.

The unitary method is a method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value.

Sam bought a baseball glove for $35. That is 7 times as much as he paid for a baseball.

Let x be the price of the baseball:

The equation form

7x = 35

x = 35/7

x= 5

Therefore, The ball was 5$

Learn more about the unitary method;

https://brainly.com/question/23423168

#SPJ2

(1) The altitude of the triangle is increasing at a rate of 0.4 cm/min when the altitude is 20 cm and the area is 80 cm².

(2) We can solve for (ds/dt), the rate at which the shadow is growing.

(3) We can solve for (dh/dt), the rate at which the height is growing, when h = 3 m.

(1)To find the rate at which the altitude of the triangle is increasing, we can use the formula for the area of a triangle and differentiate it with respect to time.

Let A be the area of the triangle, b be the base, and h be the altitude. We have the formula for the area of a triangle:

A = (1/2) * b * h

Differentiating both sides with respect to time t:

dA/dt = (1/2) * (db/dt) * h + (1/2) * b * (dh/dt)

Given that dA/dt = 4 cm²/min and db/dt = 1 cm/min, we can substitute these values into the equation:

4 = (1/2) * 1 * 20 * (dh/dt)

Simplifying the equation:

4 = 10 * (dh/dt)

Now we can solve for (dh/dt):

dh/dt = 4/10 = 0.4 cm/min

Therefore, the altitude of the triangle is increasing at a rate of 0.4 cm/min when the altitude is 20 cm and the area is 80 cm².

(2) To find the rate at which the man's shadow is growing, we can use similar triangles and differentiate the relationship between the height of the man, the distance between the man and the lamp post, and the length of the shadow.

Let h be the height of the man, d be the distance between the man and the lamp post, and s be the length of the shadow. We have the following similar triangles:

h/s = (h+5)/(s+d)

Differentiating both sides with respect to time t:

(dh/dt)/s = [(dh/dt) + 0]/(s + d) - (h+5)/(s+d)² * (ds/dt)

Given that dh/dt = -1.5 m/s (since the man is getting farther from the lamp post), h = 2 m, d = 10 m, and we want to find (ds/dt), the rate at which the shadow is growing, we can substitute these values into the equation:

(-1.5)/s = (-1.5)/(s+10) - (2+5)/(s+10)² * (ds/dt)

Now, we can solve for (ds/dt), the rate at which the shadow is growing.

(3) To find how fast the height of the pile is growing, we can use related rates and the formula for the volume of a cone.

Let V be the volume of the sand pile, r be the radius of the base, and h be the height of the cone. We have the formula for the volume of a cone:

V = (1/3) * π * r² * h

Differentiating both sides of the equation with respect to time t:

dV/dt = (1/3) * π * (2r * dr/dt * h + r² * dh/dt)

Given that dV/dt = 1.2 m³/min and dh/dt is what we want to find, we can substitute these values into the equation:

1.2 = (1/3) * π * (2r * dr/dt * h + r² * dh/dt)

Since the base diameter and height are always equal, we have r = h/2. Let's substitute this into the equation:

1.2 = (1/3) * π * (2(h/2) * dr/dt * h + (h/2)² * dh/dt)

Simplifying the equation:

1.2 = (1/3) * π * (h * dr/dt * h + (h²/4) * dh/dt)

1.2 = (1/3) * π * (h² * dr/dt + (h²/4) * dh/dt)

Now, we need to find the value of dr/dt, which represents the rate at which the radius of the base is changing. Since the base diameter and height are always equal, when the height is 3 m, the radius is 3/2 = 1.5 m.

Now we can solve for (dh/dt), the rate at which the height is growing, when h = 3 m.

To know more about area visit:

https://brainly.com/question/25537475

#SPJ11

a. The altitude of the triangle is increasing at a rate of -1.5 cm/min.

b. The man's shadow is increasing at a rate of 1 m/s.

c. The height of the pile is growing at a rate of 0.1698 m/min.

In Mathematics and Geometry, the area of a triangle can be calculated by using the following mathematical equation (formula):

Area of triangle = 1/2 × b × h

Where:

For the base area, we have:

b = 2(80)/20

b = 8 cm.

By taking the first derivative of the triangle's area by using product rule, we have:

dA/dt = 1/2(db/dt)h + 1/2(dh/dt)b

4 = 1/2(20) + 1/2(8)(dh/dt)

(dh/dt) = (4 - 10)/4

(dh/dt) = -1.5 cm/min.

Part B.

Let the variable x represent the distance between the man and the lamp post.

Let the variable y represent the length of the man's shadow.

Based on the basic proportionality theorem, we have:

\(\frac{5}{x+y} =\frac{2}{y}\)

5y = 2x + 2y

3y = 2x

3dy/dt = 2dx/dt

dy/dt = 1/3 × 2dx/dt

dy/dt = 2/3 × 1.5

dy/dt = 1 m/s.

Part C.

In Mathematics and Geometry, the volume of a cone can be calculated by using this formula:

Volume of cone, V = 1/3 × πr²h

Where:

Since the height and base diameter are always equal, we have:

radius = base diameter/2 = h/2

V = 1/3 × π(h/2)²h

V = πh³/12

dV/dt = 3πh²/12dh/dt

1.2 = 3 × 3.142 × (3)²/12dh/dt

dh/dt = 0.1698 m/min.

Read more on area of triangle here: brainly.com/question/12548135

#SPJ1

Answer:

no, never completely factored with negative exponents

Step-by-step explanation:

5x^-3 = 5/x^3

Answer:

YES THEY ARE SIMILAR

Step-by-step explanation:

good luck!

Answer:

I'm positive they are but I dont know for sure

Answer:

-1/2

Step-by-step explanation:

- arrange the equation in the y=mx+b form

2x + 4y =21, subtract 2x from both sides of the equation

4y= -2x +21 , divide both sides by 4

y= -1/2x +21/4

-compare the slopes m of the 2 equations

y= kx -12, has the slope k

y= -1/2x +21/4, has the slope -1/2

- If the lines are parallel then they have the same slope

Therefore, k= -1/2

Answer:

D

Step-by-step explanation:

The two angles are equal to 180 degrees

Answer:

359.2 cubic inches

Step-by-step explanation:

Answer:

3x10=30   30x178=5,430

Step-by-step explanation:

\(3 \times 10 \times 178 \\ 30 \times 178 \\ 5340 \: \: answer\)

Her gross pay is $421.38

First, we know that she gets $16 per hour, and she worked 20 hours, then she gets:

20*$16 = $320

Now we also know that she receives a percentage of 8% of the gratuities, and the gratuities totaled $1,267.28

The 8% of $1,267.28 is:

$1,267.28*(8%/100%) = $1,267.28*0.08 = $101.38

Her gross pay is:

P = $101.38 + $320 = $421.38

If you want to learn more about percentages:

https://brainly.com/question/843074

#SPJ1

Answer:

891p

Step-by-step explanation:

1bag=99p

9bags=99x9

=891p

Answer:

3

Step-by-step explanation:

Solve for m.

3x + 4 = mx + 4 subtract 4 from each side

3x + 4 - 4 = mx + 4 - 4 the 4’s on both sides will cancel

3x = mx divide each side by x

3x/x = mx/x The x cancels and you’re left with

3 = m

If m = 3 then

3x + 4 = mx + 4 will become

3x + 4 = 3x + 4 subtract 4 from each side

3x + 4 - 4 = 3x + 4 - 4 the 4’s on both sides will cancel

3x = 3x divide each side by 3

3x/3 = 3x/3 The 3s cancel and you’re left with

x = x

So for any value of x, positive or negative, they will equal each other. Therefore there are an infinite number of solutions when m = 3

Option D (9) is not a probability and is not a possible answer choice for a probability question.

To find the probability of the intersection of events A and B (denoted as P(A ∩ B)), we need to know how many elements are in both A and B. Since there are 2 repeated elements between the events, this means that there are a total of 7 - 2 = 5 distinct elements between them.

Therefore, P(A ∩ B) = 5/7.

Note that none of the answer choices provided match this result exactly. Option A is the closest with a probability of 4/7, but this is the probability of A alone, not the intersection of A and B. Option B (2/7) is the probability of B alone and option C (5/7) is the probability of either A or B occurring, not the intersection.

Know more about probability here:

https://brainly.com/question/30034780

#SPJ11

Answer:

Step-by-step explanation:

4n - 1 ≤ 9

≤  -----> this symbol stands for greater than or equal to

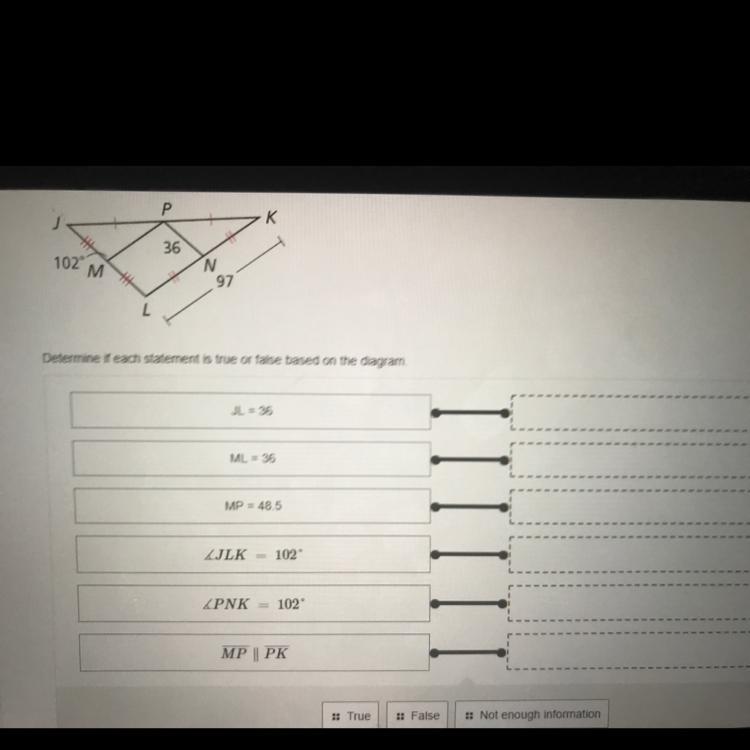
Answer:

Step-by-step explanation:

1). JL = 36

   Reason : Since, PN is the segment joining midpoints of sides JK and LK,

   Therefore, JL = 2(PN)

   JL = 2(36)

   JL = 72

   False.

2). ML = 36

    Reason: Since, ML = \(\frac{1}{2}(JL)\)

    ML = \(\frac{1}{2}(72)\)

          = 36

    True.

3). MP = 48.5

    Reason : By the same property, MP = \(\frac{1}{2}(LK)\)

    MP = \(\frac{97}{2}\)

    MP = 48.5

    True.

4). ∠JLK = 102°

    Reason: Segment joining midpoints of two sides of a triangle is parallel and measures half of the third side of the triangle.

     Since, PM║LK and JL is a transversal line,

     ∠JMP ≅ ∠JLK [Corresponding angles]

     m∠JLK = 102°

     True.

5). ∠PNK = 102°

    Reason : Since, PN║JL and LK is a transversal line,

    ∠JLK ≅ ∠PNK [Corresponding angles]

    ∠PNK = 102°

     True.

6). MP║PK

    Reason : MP and PK are intersecting each other at P.

    Therefore, they can not be parallel.

     False.

The y-intercept in this model is 20, representing the fixed one-time registration fee for participating in the local bowling league.

In the given equation y = 15x + 20, where y represents the monthly fee and x represents an unspecified variable, the y-intercept can be identified by setting x = 0. When x = 0, the equation becomes y = 15(0) + 20, which simplifies to y = 20.

Interpreting the y-intercept, we can conclude that the y-intercept in this model is 20. This means that even without any additional factors or considerations (represented by the variable x), there is a fixed cost of $20 associated with participating in a local bowling league. This fixed cost, likely referred to as a one-time registration fee, is incurred at the beginning of joining the league and is not affected by any other factors such as the duration or specific features of the league.

Therefore, the y-intercept of 20 indicates the baseline cost or the starting point for the monthly fee in the bowling league model, reflecting the required one-time registration fee that participants need to pay.

To learn more about y-intercept

https://brainly.com/question/14180189

#SPJ8

Answer:

286.5 meters taller than Ruben.

Step-by-step explanation:

We can use the Pythagorean theorem to solve this problem. Let's call the height of the statue "h". Then we have:

h^2 + 24^2 = (h+25)^2

Expanding the right side:

h^2 + 576 = h^2 + 50h + 625

Subtracting h^2 from both sides:

576 = 50h + 625

Subtracting 625 from both sides:

-49 = 50h

Dividing by 50:

h = -0.98

Since a negative height doesn't make sense in this context, we made an error in our calculations. Let's try again, using the fact that the distance between the top of the statue and Ruben's head is 1 meter:

h^2 + 24^2 = (h+1)^2

Expanding the right side:

h^2 + 576 = h^2 + 2h + 1

Subtracting h^2 from both sides:

576 = 2h + 1

Subtracting 1 from both sides:

575 = 2h

Dividing by 2:

h = 287.5

Answer:

\(y = \frac{-3}{4}x + 36\)

Step-by-step explanation:

Data provided in the question

Height = 36 inches

Stant of the stairs followed that declines 9 inches for every 12 horizontal inches

Height = x

x =  from top of the stairs

based on the above information

Therefore the change in rate is

\(\frac{-9}{12} = \frac{-3}{4}\)

It depicts the line sloping.

Now the function would be determined by the line equation which is as follows

y = mx+c

\(m = \frac{-3}{4}\)

where,

c = 36 inches

So, the function is

\(y = \frac{-3}{4}x + 36\)

Answer:

Answer is A

Step-by-step explanation:

Answer:

D. 17

Step-by-step explanation:

No-

Sally's total pay for working 49 hours, with a regular hourly rate of $12.00 per hour and an overtime rate of 1.5 times the regular hourly rate, is $642.00.

To find out how many Canadian dollars Ann will need to buy 1000 euros, we can use the given exchange rate of 1 Canadian dollar = 0.694 euros.

The calculation is as follows:

Amount in Canadian dollars = Amount in euros / Exchange rate

Substituting the values:

Amount in Canadian dollars = 1000 euros / 0.694 euros per Canadian dollar

Simplifying the expression:

Amount in Canadian dollars = 1440.692

Therefore, Ann will need approximately 1440.692 Canadian dollars to buy 1000 euros.

Now let's calculate Sally's total pay based on her work hours, regular hourly rate, and overtime rate.

Sally worked 49 hours, and a regular work week consists of 40 hours. So, she worked 9 hours of overtime.

Her regular hourly rate is $12.00 per hour, and the overtime hourly rate is 1.5 times the regular hourly rate, which is $18.00 per hour.

To calculate her total pay, we need to consider her regular hours and overtime hours.

Regular pay = Regular hours * Regular hourly rate

Regular pay = 40 hours * $12.00 per hour = $480.00

Overtime pay = Overtime hours * Overtime hourly rate

Overtime pay = 9 hours * $18.00 per hour = $162.00

Total pay = Regular pay + Overtime pay

Total pay = $480.00 + $162.00 = $642.00

Therefore, Sally's total pay for working 49 hours, with a regular hourly rate of $12.00 per hour and an overtime rate of 1.5 times the regular hourly rate, is $642.00.

Learn more about pay here

https://brainly.com/question/16134508

#SPJ11

Answer:

Step-by-step explanation:

For two lines to be parallel their slopes must be equal. For two lines to be perpendicular their slopes must be the negative reciprocal of each other.

Step 1 Find the slope of the equation.

Put it into the slope-intercept form. y = mx + b.  

For x-y = 7, move the x to the left; therefore subtract the x from both sides. this leaves you  -y = -x + 7

Then, divide both sides by -1 to get a positive y.  -y/-1 = (-x + 7)/-1

This leaves y = x - 7  The slope(m) for this equation is m = 1

The other equation must also have a slope of 1 or m=1 for the lines to be parallel.

Use the point given to you (-7, -6) and substitute for (x, y)

The slope-intercept form y = mx + b can once again be used.

x = -7, y =-6, and slope or m = 1

Therefore,  y = mx + b substituted will be -6 = (1)(-7) + b; now, solve for b which is the y intercept

-6 = -7 + b add 7 to both sides -6 +7 = -7 + b +7 ; therefore, b = 1

Now you know the slope(m) which is equal to 1 and the y-intercept(b) which is equal to 1.

Finally, substitute the m and b in the slope-intercept form

            y = (1)x + 1 or y = x +1

Answer:

90 balls

Step-by-step explanation:

simply add them

Answer: 90 balls

Step-by-step explanation:

30 + 10 = 40

40 + 50 = 90.