Answers
Answer:
(x - 3)² + (y + 5)² = 10
Step-by-step explanation:
The equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k) are the coordinates of the centre and r is the radius
Here (h, k) = (3, - 5 ) , then
(x - 3)² + (y - (- 5) )² = r² , that is
(x - 3)² + (y + 5)² = r²
r is the distance from the centre to a point on the line
Calculate r using the distance formula
r = \(\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\)
with (x₁, y₁ ) = (3, - 5) and (x₂, y₂ ) = (6, - 4)
r = \(\sqrt{(6-3)^2+(-4+5)^2}\)
= \(\sqrt{3^2+1^2}\)
= \(\sqrt{9+1}\)
= \(\sqrt{10}\) ⇒ r² = (\(\sqrt{10}\) )² = 10
(x - 3)² + (y + 5)² = 10 ← equation of circle
Related Questions
Solve for x. 7x=28 4x=48
Answers
Answer: x=4
x=12
Step-by-step explanation:
7x=28
divide 7 on both sides
28/7=4
x=4
4x=48
divide 4 on both sides
48/4=12
x=12
x=4 for the first one because you have to separate the 7 from x so to do that you would have to divide 7 from both sides to get x by itself. Same for the second one, x would = 12 because when you divide 4 from 48 in order to get x by itself.
You bought a used truck for $15,000. The value of the truck will decrease each year because of depreciation. The truck depreciates at the rate of 8% per year estimate the value of the truck in 5 years
Answers
Answer: $9886.22
Step-by-step explanation:
Breast-feeding mothers secrete calcium into their milk. Some of the calcium may come from their bones, so mothers may lose bone mineral. Researchers measured the percent change in mineral content of the spines of 47 mothers during three months of breast-feeding.6Here are the data:
Blend Images/Superstock
(a)
The researchers are willing to consider these 47 women as an SRS from the population of all nursing mothers. Suppose that the percent change in this population has standard deviation ? = 2.5%. Make a stemplot of the data to verify that the data follow a Normal distribution quite closely. (Don
Answers
To create a stemplot, we first need to separate the data into "stems" and "leaves." Each stem represents the first digit(s) of each data point, while each leaf represents the last digit(s). For example, if the data point is 12.3, the stem would be 12 and the leaf would be 3.
To make a stemplot, the data should be arranged in increasing order, and then separated into stems and leaves.
STEMPLOT OF THE DATAHowever, you can use the data given and arrange it in increasing order and separate it into stems and leaves to make a stemplot. A stemplot is a good way to check if the data follow a normal distribution quite closely, the more the data is spread out and the more symmetric it is, the more likely it is to follow a normal distribution.
Also, it is important to mention that from the given data, it is not possible to conclude if the percent change in this population has standard deviation of 2.5%. This parameter can only be estimated from a sample if it follows a normal distribution which is not clear from the given data.
Learn more about Stemplot here:
https://brainly.com/question/29174445
#SPJ4
how so u simplify in math
Answers
Answer:
Remove any grouping symbol such as brackets and parentheses by multiplying factors.
Use the exponent rule to remove grouping if the terms are containing exponents.
Combine the like terms by addition or subtraction.
Combine the constants.
simplify the expression. make sure to show all steps. write in standard form.
thanks

Answers
Answer:
54i - 8
Step-by-step explanation:
6*9i + 4i*2i
=54i + 8i^2
= 54i - 8
when calculating centered moving-averages using a 4-period moving average, how many data points are lost at the beginning of the original series? multiple choice 4 none of the options are correct. 1 2 3
Answers
In linear equation, the no of points which are lost at both end of the original series in 2.
What in mathematics is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept.Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.linear function is defined as a function that has either one or two variables without exponents. It is a function that graphs to the straight line.When calculating centered moving average using 4 - period moving average .
the no of points which are lost at both end of the original series in 2..
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
Use the function to fill in the table.
g(x)=-3x+1

Answers
Triangle LMN has a vertical height of 2 units and a horizontal length of 3 units. Triangle NOP has a vertical height of 4 units and an unknown horizontal length.
Answers
Answer:
32
Step-by-step explanation:
What is the answer to this question?
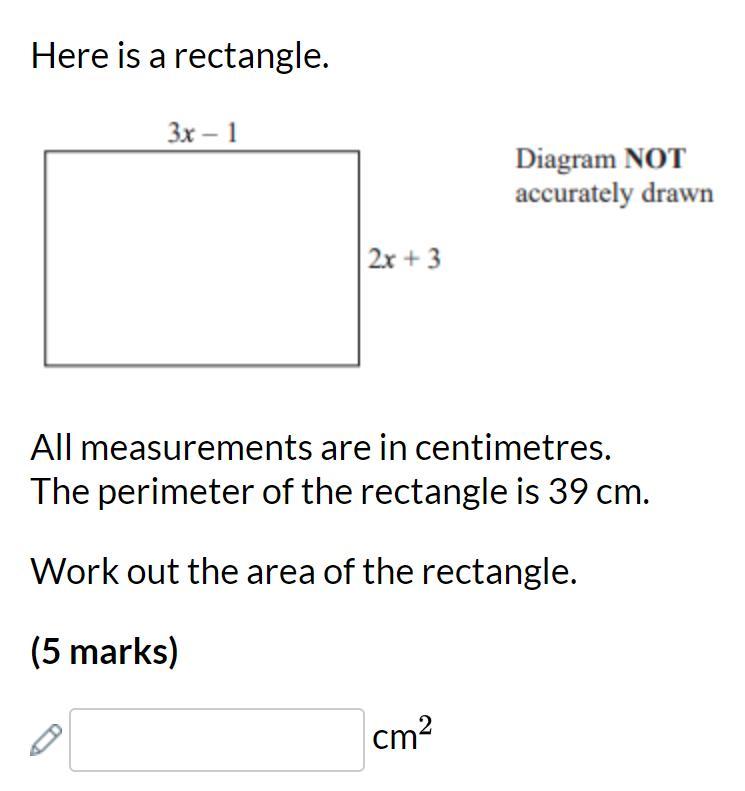
Answers
Answer:
95 cm^2
Step-by-step explanation:
perimeter(p)=39cm
L=3x-1
B=2x+3
Now,
p=2(l+b)
39=2(3x-1+2x+3)
39=6x-2+4x+6
39=10x+4
39-4=10x
x=35/10
x=3.5
Putting the value of x
L=3x-1; =3×3.5-1; =10.5-1; =9.5cm
B =2x+3; =2×3.5+3; =7+3; =10cm
Again,
A= L×B
=9.5×10
=95cm^2
Which graph best represents the function f(x) = (x + 2)(x − 2)(x − 3)?
Answers
Answer:
The graph should sort of look like the image bellow
Step-by-step explanation:
Since it is a cubic function, the graph would curve up on into the shape of a palabora, come back down, and go up again.

Graph crossing the x-axis at (-2, 0), (2, 0) and (3, 0) will be the correct choice.
Equation of a graph in factored form: If the equation of a graph is given in the factored form,
f(x) = (x - a)(x - b)(x - c)
Roots (where the graph crosses or touches the x-axis) of the
equation will be x = a, b, c
Given in the question,
Equation of the graph → f(x) = (x + 2)(x -2)(x - 3)
For zeros of the equation, equate the equation with zero.
f(x) = (x + 2)(x -2)(x - 3) = 0
x = -2, 2, 3
Therefore, graph having zeros at (-2, 0), (2, 0) and (3, 0) will be correct graph.
Learn more about the graph of a function here,
https://brainly.com/question/12543560?referrer=searchResults

value of x...........
in given rhombus.

Answers
Step-by-step explanation:
we know that,
《opposite angle are equal in a rhombus 》
HERE,
one angle =2x
Opposite angle =3x-40
According to the question,
\(\tt{ 2x=3x-40 }\)
\(\tt{3x=2x+40 }\)
\(\tt{3x-2x=40 }\)
\(\tt{ x=40 }\)
#quality answer
\(\boxed{\large{\bold{\blue{ANSWER~:) }}}}\)
In this given rhombus,
one angle =2x°another angle(opposite angle) =3x-40°we know that
\(\boxed{\sf{opposite~ angle~ are~ equal ~in~ a~ rhombus }}\)
According to the question,
one angle=opposite angle 2x=3x-402x-3x=-40-x=-40x=40°Therefore.
The value of x In the given rhombus is 40°
Isabel is buying framing to go around the perimeter of one of her paintings. Each inch of framing costs $0.40. What is the total cost of the framing for the pantings
Answers
I have added the complete question. That is in the attachment
Answer:
$13.2
Step-by-step explanation:
Cost of 1 inch = $0.4
Perimeter of painting is same as perimeter of a rectangle since painting is a rectangle
Perimeter = 2(l+b)
L = 10¼
B = 6¼
P = 2(10¼ + 6¼)
P = 2(41/4 + 25/4)
P = 2(10.25 + 6.25)
P = 2(16.5)
P = 33
Total cost of framing
= 0.4 x 33
= $13.2

Would the midpoint (2,2) be correct?

Answers
Answer: YES, Its correct.
\(M_x=\frac{-6+2}{2}=2\\\\M_y=\frac{-3+7}{2}=2\\\\M=(2,2)\)
Answer:
(-2,2)
Step-by-step explanation:
The midpoint is the middle of the line. So, you can take it step-by-step and look at the individual numbers.
Between -6 and 2, that is 8 spaces. So, the middle would be four spaces from one of those numbers. Therefore, X-COORDINATE = -2
Between -3 and 7, that is 10 spaces. So the middle would be 5 spaces from one of those numbers, Therefore, Y-COORDINATE = 2
So, the midpoint would be (-2,2)
What is the simplest form of
2(3x-2y) + 3(x-3y)
Answers
Answer:
9x - 13y
Step-by-step explanation:
2(3x - 2y) + 3(x - 3y)
Use distributive law a(b + c) = ab + ac
⇒ 2·3x - 2·2y + 3·x - 3·3y
⇒ 6x - 4y + 3x - 9y
Gather like terms:
⇒ 6x + 3x - 4y - 9y
Combine like terms:
⇒ 9x - 13y
..........................
Answers
Answer:
blue
Step-by-step explanation:
Problem 1 . Prove the following proposition. Proposition 1 Let I⊆R be an interval and f,g two real-valued functions defined on I. Assume that f and g are convex. Then: (a) The function f+g is convex. (b) If c≥0, then cf is convex. (c) If c≤0, then cf is concave.
Answers
It is shown that: (a) The function f+g is convex.
(b) If c ≥ 0, then cf is convex. (c) If c ≤ 0, then cf is concave. The proposition is proven.
How did we prove the proposition?To prove the proposition, we'll need to show that each part (a), (b), and (c) holds true. Let's start with part (a).
(a) The function f+g is convex:
To prove that the sum of two convex functions is convex, we'll use the definition of convexity. Let's consider two points, x and y, in the interval I, and a scalar λ ∈ [0, 1]. We need to show that:
\((f+g)(λx + (1-λ)y) ≤ λ(f+g)(x) + (1-λ)(f+g)(y)\)
Now, since f and g are both convex, we have:
\(f(λx + (1-λ)y) ≤ λf(x) + (1-λ)f(y) \: (1) \\
g(λx + (1-λ)y) ≤ λg(x) + (1-λ)g(y) \: (2)\)
Adding equations (1) and (2), we get:
\(f(λx + (1-λ)y) + g(λx + (1-λ)y) ≤ λf(x) + (1-λ)f(y) + λg(x) + (1-λ)g(y) \\
(f+g)(λx + (1-λ)y) ≤ λ(f+g)(x) + (1-λ)(f+g)(y)\)
This shows that
\((f+g)(λx + (1-λ)y) ≤ λ(f+g)(x) + (1-λ)(f+g)(y),\)
which means that f+g is convex.
(b) If c ≥ 0, then cf is convex:
To prove this, let's consider a scalar λ ∈ [0, 1] and two points x, y ∈ I. We need to show that:
\((cf)(λx + (1-λ)y) ≤ λ(cf)(x) + (1-λ)(cf)(y)\)
Since f is convex, we know that:
\(f(λx + (1-λ)y) ≤ λf(x) + (1-λ)f(y)\)
Now, since c ≥ 0, multiplying both sides of the above inequality by c gives us:
\(cf(λx + (1-λ)y) ≤ c(λf(x) + (1-λ)f(y))
\\ (cf)(λx + (1-λ)y) ≤ λ(cf)(x) + (1-λ)(cf)(y)
\)
This shows that cf is convex when c ≥ 0.
(c) If c ≤ 0, then cf is concave:
To prove this, we'll consider the negative of the function cf, which is (-cf). From part (b), we know that (-cf) is convex when c ≥ 0. However, if c ≤ 0, then (-c) ≥ 0, so (-cf) is convex. Since the negative of a convex function is concave, we conclude that cf is concave when c ≤ 0.
In summary, we have shown that:
(a) The function f+g is convex.
(b) If c ≥ 0, then cf is convex.
(c) If c ≤ 0, then cf is concave.
Therefore, the proposition is proven.
learn more about convex function: https://brainly.com/question/26093364
#SPJ4
a) This implies that (f + g)(λx + (1 - λ)y) ≤ λ(f(x) + g(x)) + (1 - λ)(f(y) + g(y)), which proves that f + g is convex, b) This implies that (cf)(λx + (1 - λ)y) ≤ λ(cf(x)) + (1 - λ)(cf(y)), proving that cf is conve, c) Therefore, Proposition 1 is proven, demonstrating that the function f + g is convex, cf is convex when c ≥ 0, and cf is concave when c ≤ 0.
To prove Proposition 1, we will demonstrate each part individually:
(a) To prove that the function f + g is convex, we need to show that for any x, y in the interval I and any λ ∈ [0, 1], the following inequality holds:
(f + g)(λx + (1 - λ)y) ≤ λ(f(x) + g(x)) + (1 - λ)(f(y) + g(y))
Since f and g are convex functions, we know that for any x, y in I and λ ∈ [0, 1], we have:
f(λx + (1 - λ)y) ≤ λf(x) + (1 - λ)f(y)
g(λx + (1 - λ)y) ≤ λg(x) + (1 - λ)g(y)
By adding these two inequalities together, we obtain:
f(λx + (1 - λ)y) + g(λx + (1 - λ)y) ≤ λf(x) + (1 - λ)f(y) + λg(x) + (1 - λ)g(y)
This implies that (f + g)(λx + (1 - λ)y) ≤ λ(f(x) + g(x)) + (1 - λ)(f(y) + g(y)), which proves that f + g is convex.
(b) To prove that cf is convex when c ≥ 0, we need to show that for any x, y in I and any λ ∈ [0, 1], the following inequality holds:
(cf)(λx + (1 - λ)y) ≤ λ(cf(x)) + (1 - λ)(cf(y))
Since f is a convex function, we have:
f(λx + (1 - λ)y) ≤ λf(x) + (1 - λ)f(y)
By multiplying both sides of this inequality by c (which is non-negative), we obtain:
cf(λx + (1 - λ)y) ≤ c(λf(x)) + c((1 - λ)f(y))
This implies that (cf)(λx + (1 - λ)y) ≤ λ(cf(x)) + (1 - λ)(cf(y)), proving that cf is convex when c ≥ 0.
(c) To prove that cf is concave when c ≤ 0, we can use a similar approach as in part (b). By multiplying both sides of the inequality f(λx + (1 - λ)y) ≤ λf(x) + (1 - λ)f(y) by c (which is non-positive), we obtain the inequality (cf)(λx + (1 - λ)y) ≥ λ(cf(x)) + (1 - λ)(cf(y)), showing that cf is concave when c ≤ 0.
Therefore, Proposition 1 is proven, demonstrating that the function f + g is convex, cf is convex when c ≥ 0, and cf is concave when c ≤ 0.
Learn more about concave here:
https://brainly.com/question/27841226
#SPJ11
what is the slope of the line tangent to the graph of y=x2−2x2 1 when x = 1 ?
Answers
The slope of the line tangent to the graph of \(y = x^2 - 2x + 1\) when \(x = 1\) is 2.
1. Take the derivative of the given function: \(y' = 2x - 2\).
2. Substitute \(x = 1\) into the derivative: \(y' = 2(1) - 2 = 2\).
To find the slope of the tangent line, we need to differentiate the given function with respect to \(x\). The derivative of \(x^2\) is \(2x\), and the derivative of \(-2x\) is \(-2\). Therefore, the derivative of \(y = x^2 - 2x + 1\) is \(y' = 2x - 2\).
Next, we substitute \(x = 1\) into the derivative to find the slope at that point. By plugging in \(x = 1\) into the derivative, we get \(y' = 2(1) - 2 = 2\). Thus, the slope of the tangent line at \(x = 1\) is 2.
To learn more about tangent line click here brainly.com/question/31326507?
#SPJ11
A sample of size n = 79 is drawn from a population whose standard deviation is 0 = 9, Part 1 of 2 (a) Find the margin of error for a 95% confidence interval for μ. Round the answer to at least three decimal places. The margin of error for a 95% confidence interval for μl is Part 2 of 2 (b) If the sample size were 1 = 89, would the margin of error be larger or smaller?
Answers
(a) The margin of error for a 95% confidence interval for μ ≈ 2.034
(b) If the sample size were increased to n = 89, the margin of error would be smaller.
(a) To calculate the margin of error for a 95% confidence interval for μ, we can use the formula:
Margin of Error = z * (σ / sqrt(n))
Where:
- z is the z-score corresponding to the desired confidence level (95% confidence level corresponds to z = 1.96)
- σ is the population standard deviation
- n is the sample size
Provided:
- σ = 9
- n = 79
- z = 1.96
Substituting the values into the formula:
Margin of Error = 1.96 * (9 / sqrt(79))
Margin of Error ≈ 2.034
So, the margin of error for a 95% confidence interval for μ is approximately 2.034 (rounded to at least three decimal places).
(b) As the sample size increases, the standard error decreases, resulting in a smaller margin of error.
This is because the margin of error is inversely proportional to the square root of the sample size.
To know more about margin of error refer here:
https://brainly.com/question/29419047#
#SPJ11

triangle qrs is similar to triangle xyz . the measure of ∠x is 75° and the measure of ∠q is equal to 5(n−3)° . which is the value of n
Answers
The two triangles n = (75 + 3) / 5 = 18. The measure of angle q is 18 degrees.
1. First, find the value of n by using the equation 5(n - 3) = 75 + 3
2. Next, add 75 and 3 together and divide by 5. This gives us a value of 18 for n.
3. Finally, use the equation 5(n - 3) to determine the measure of angle q in triangle qrs. This equals 5(18 - 3) = 5(15) = 75 degrees.
The two triangles qrs and xyz are similar, meaning they have the same angle measures. In order to find the measure of angle q in triangle qrs, we must first find the value of n. The measure of angle x in triangle xyz is 75 degrees and the measure of angle q in triangle qrs is equal to 5(n - 3) degrees. We can use this equation to solve for the value of n. To do this, we add 75 and 3, then divide by 5. This gives us a value of 18 for n. Therefore, the measure of angle q in triangle qrs is 18 degrees.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
i dont understand this question im very bad at maths

Answers
so it’s 2400
2400cm³
Step-by-step explanation:\(Volume=15\times 20\times 8\)\(=300\times 8\\ =2400cm^3\)
\((Analyze\ the\ information\ carefully)\)
I hope this helps you
:)
When using a one-sample t-procedure to construct a confidence interval for the mean of a finite population, a condition is that the population size be at least 10 times the sample size. The reason for the condition is to ensure that
a. The sample size large enough
b. The central limit theorem is applicable for the sample mean
c. The sample standar deviation is good apporximation of the population standar deviation
d. The degree dependence among observations is negligible
e. The sampling method is not biased
Answers
The correct answer is (b) The central limit theorem is applicable for the sample mean.
The condition that the population size be at least 10 times the sample size is necessary to ensure that the sample mean follows a normal distribution, as required by the central limit theorem. The central limit theorem states that the sample mean will be approximately normally distributed, regardless of the underlying population distribution, as long as the sample size is large enough. In this case, the condition is necessary to ensure that the sample size is sufficiently large for the central limit theorem to be applicable. Options (a), (c), (d), and (e) are not the correct answers because they do not directly relate to the condition that the population size be at least 10 times the sample size.
To learn more about central limit theorem click here
brainly.com/question/18403552
#SPJ4
WILL GIVE BRAINLIEST (PLEASE SHOW WORK)
Evaluate sec (11pi/6) without using technology
Answers

6.) what is the kb when the ka of a solution is 5.47×10−4. (ka = 5.47×10−4)
Answers
The value of Kb will be 1.83 × 10⁻¹¹.
The given problem states that Ka is equal to 5.47×10⁻⁴, and the task is to find Kb. Ka and Kb are related to each other through the equation Kw = Ka × Kb. Kw represents the ion product of water, which is equal to the concentration of H₃O⁺ ions multiplied by the concentration of OH⁻ ions. It has a value of 1.0 × 10⁻¹⁴.
Using the fact that pKw = pH + pOH = 14.00, we can determine the relationship between pKa and pKb. By rearranging the equation, we get pKa + pKb = 14.00. This equation relates the logarithms of the acid dissociation constant (pKa) and the base dissociation constant (pKb).
To find Kb, we can use the formula Kb = Kw/Ka. Substituting the given values, we have Kb = (1.0 × 10⁻¹⁴)/(5.47 × 10⁻⁴). Simplifying this expression, we find Kb = 1.83 × 10⁻¹¹.
Therefore, the value of Kb is determined to be 1.83 × 10⁻¹¹.
To learn more about value, refer below:
https://brainly.com/question/30145972
#SPJ11
Bryant Industries uses forecasting to estimate the number of orders that will be placed by their customers. The table below gives the sales figures for the last four months. Month 2 3 4 5 Sales 924 91
Answers
Bryant Industries uses forecasting to estimate the number of orders that will be placed by their customers. The table below gives the sales figures for the last four months.Month2345Sales92491942004There are different forecasting techniques used by companies like Bryant Industries to predict future sales.
One of the most widely used methods is the time-series method. This method is particularly useful when the demand for a product or service changes over time and when there are no external factors that affect the sales. In this case, we can use a time-series method called the moving average to estimate future sales. The moving average is a time-series method that uses the average of past sales data to estimate future sales. It is particularly useful when there are no external factors that affect the sales. In this case, we can use a 3-month moving average to estimate future sales. The 3-month moving average is calculated as follows: (924 + 919 + 420) / 3 = 754.33. This means that we can expect sales of around 754 units next month. The moving average method is easy to use and is a good way to get a quick estimate of future sales. However, it has some limitations. For example, it does not take into account external factors that may affect sales, such as changes in the economy or in consumer behavior.
In conclusion, Bryant Industries can use the moving average method to estimate future sales. However, they should also consider other factors that may affect sales, such as changes in the economy or in consumer behavior. By doing so, they can make more accurate forecasts and improve their overall performance.
To learn more about time-series method visit:
brainly.com/question/32443421
#SPJ11
which of the following is true regarding dot plots and histograms? multiple choice question. dot plots work better for large data sets. dot plots do not lose the identity of individual observations. histograms are easier to construct.
Answers
Dot plots are better suited for maintaining the identity of individual observations, especially in smaller data sets, while histograms are useful for visualizing the distribution of larger data sets, even though they lose the identity of each specific data point.
Regarding dot plots and histograms, the true statement is that dot plots do not lose the identity of individual observations. Dot plots display each data point as a dot on a number line or axis, preserving information about individual data points. This is especially useful when dealing with small to moderate-sized data sets, as it allows for easy identification of patterns, clusters, or outliers.
On the other hand, histograms are a graphical representation that organizes data into intervals or bins, which can provide an overview of the distribution of a larger data set. While histograms are often easier to construct and can help visualize patterns and trends for large data sets, they lose the identity of individual observations, as the data points are grouped together in bins.
In summary, dot plots are better suited for maintaining the identity of individual observations, especially in smaller data sets, while histograms are useful for visualizing the distribution of larger data sets, even though they lose the identity of each specific data point.
To learn more about Dot plots click here
brainly.com/question/22746300
#SPJ11
Find the value of x and y in the parallelogram below.

Answers
Y-3=129
Y=132
————————
-x+4=92
-x=92-4
X=-88
Solution
Y=132
X=-88
Sara's having a barbecue and she cooks burgers. She buys a 6 pack of breadrolls and a 10 pack of burger meat. How can sara get the same amount of burger to bread rolls
Answers
Answer:
Buying 5 packs of bread rolls and 3 packs of burger meat
Step-by-step explanation:
Sara needs to find the least common multiple between 6 bread rolls and 10 pieces of burger meat:
\(LCM:\\10\ 6\ |2\\5\ \ 3\ |3\\5\ \ 1\ |5\\1\ \ 1\ |1\\\\LCM = 2*3*5=30\)
Sara will get the same amount of burger to bread rolls when she buys 30 units of each. The numbers of packs of each product that she must buy are:
\(B=\frac{30}{6}=5\ packs\\ M=\frac{30}{10}=3\ packs\)
Sara should buy 5 packs of bread rolls and 3 packs of burger meat.
how long will it take a $2 000 investment to earn $544 in interest at a 1.7 interest rate
Answers
Answer:
16 years
Step-by-step explanation:
1.7% of 2000 is $34
$544 divided by $34 = 16 years, that is if the interest is yearly and not monthly though
It will take 16 years for a $2,000 investment to earn $544 in interest at a 1.7% interest rate.
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Given that it take a $2 000 investment to earn $544 in interest at a 1.7 interest rate.
We have to find the time.
We can use the simple interest formula to solve this problem:
I = Prt
where I is the interest earned,
P is the principal,
r is the interest rate per time period, and
t is the time period.
Given that Principle amount = $2,000,
Interest I = $544, and
Interest rate r = 1.7% per year.
Percentage value is converted to decimal by dividing with 100.
1.7/100=0.017
We need to find t in years.
Substituting the given values into the formula, we get:
544 = 2,000 × 0.017t
544=34t
Divide both sides by 34
t = 544 /34
t = 16
Therefore, it will take 16 years for a $2,000 investment to earn $544 in interest at a 1.7% interest rate.
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ2
Line r is parallel to line c.

Answers
Answer: C
Step-by-step explanation:
what percent of northeastern students do five years
