Determine whether the given value is a sample statistic or a population parameter. A researcher examines the records of all the registered voters in one city and finds that 43% are registered Democrats. Group of answer choices
Answers
Answer: Population parameter
Step-by-step explanation: The parameter can be defined as a numerical value used to describe an entire population. The population describes all the entire values or members belonging to a particular group. Hence, numerical values which are used to explain the characteristic of the population is called the population parameter. Sample statistics on the other hand are numerical values associated statistical properties of a sample which is a subset of a certain population.
In the instance given above, 43% represents the population parameter which describes the percentage number of Democratic voters out of the entire population of voters in the city.
Related Questions
if x°,2x°and 30°are the angles of triangle ,find x°and 2x°
Answers
Answer:
x° = 50° 2x°= 100°
Step-by-step explanation:
sum of all angle of triangle = 180° therefore
x° + 2x° + 30° =180°
3x° = 180° - 30°
3x = 150°
x = 50°
2x = 100
please help asapppppppppppppp

Answers
If we perform the vertical line test, we can see that every line touches the graph once. This means that the graph is a graph of a function.
Answer choice b is correct.
100 + 100 + 100 + 1000 = X
Answers
Answer:
1300=X
Step-by-step explanation:
Answer:
1,300
Step-by-step explanation:
You would first start off with adding 100 + 100= 200. Then you would add another 100 to 200 which is 300. Then comes the final step which is adding 1000 to 300 which = 1300
X= 1,300
many elementary school students in a school district currently have ear infections. a random sample of children in two different schools found that 11 of 40 at one school and 12 of 30 at the other have ear infections. at the 0.05 level of significance, is there sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools?
Answers
Since the p-value is greater than the significance level of 0.05, we fail to reject the null hypothesis. Therefore, there is not sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools.
To determine if there is sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools, we can use a two-sample z-test for the difference in proportions.
The null hypothesis is that there is no difference between the proportions of students with ear infections at the two schools, while the alternative hypothesis is that there is a difference.
Let p1 be the proportion of students with ear infections at the first school and p2 be the proportion at the second school. The test statistic is given by:
z = (p1 - p2) / sqrt(p_hat * (1 - p_hat) * (1/n1 + 1/n2))
where p_hat is the pooled proportion, n1 and n2 are the sample sizes from the first and second schools, respectively.
The pooled proportion is given by:
p_hat = (x1 + x2) / (n1 + n2)
where x1 and x2 are the number of students with ear infections in each school.
Using the given data, we have:
n1 = 40, n2 = 30
x1 = 11, x2 = 12
p1 = x1/n1 = 11/40 = 0.275
p2 = x2/n2 = 12/30 = 0.4
p_hat = (x1 + x2) / (n1 + n2) = (11 + 12) / (40 + 30) = 0.355
The test statistic is:
z = (0.275 - 0.4) / sqrt(0.355 * 0.645 * (1/40 + 1/30)) = -1.197
Using a standard normal table or calculator, the p-value for a two-tailed test with a test statistic of -1.197 is approximately 0.231.
To know more about null hypothesis,
https://brainly.com/question/17157597
#SPJ11
Breandan miguel and heron run around the track they start at the same place and at the same time they each run at a steady rate brendan completes a lap in 4 minutes Miguel completes a lap in 6 minutes and heron competeles a lap in 3 minutes the boys wnay to know how many minutes it will take after they start running until they complete a lap at the same time
Answers
It will take them 12 minutes to complete a lap at the same time.
Describe prime factor?A prime factor is any non-zero natural integer that can be divided only by itself and by 1. Actually, a few of the initial prime numbers are and so forth. a sum which has been doubled to yield a new sum.
For example, if we divide 15 by Three and 5, you get 3 -5 = 15. major components: All prime but non-composite components are referred to as prime factors. a few 30 prime factors2, 3, or 5 are. It is essential to list 2 twice as (2 2 3 (or (22 3) in order to factors 12 since only 2 и 3 were primary elements of 12. 2 + 3 cannot be added to make 12.
Finding the lowest common multiple of the time required for each person to do a lap will help us determine how long it will take Sean, Luis, and Heron to finish a lap simultaneously.
Brendan requires four minutes to complete a lap.
For Miguel, a lap takes 6 minutes to complete.
Heron need three minutes to finish a lap.
With 4, 6, & 3 as the LCM is 12. As a result, it will take Rory, Miguel, and Heron 12 minutes to finish a lap simultaneously.
To know more about prime factor visit:
brainly.com/question/29775157
#SPJ1
3(10 + 2) could be used to simplify which of the following problems? 130(26) 13(12) 13(20)
Answers
Answer:130(26).
Step-by-step explanation: It could basically be used to simplify 130(26) because if you multiply the number on the outside of the parentheses (13) with the numbers inside the parenthesis(10+2), you will get 130(26).
The data below represents the ages of the first 10 people in the line at the movie theater 22 30 23 22 27 27 29 23 30 22, I will give brainlest for who give me tightest answer thank you.
Answers
Answer: The mean is 25.5, the mode is 22, and the median is 25.
Step-by-step explanation: When finding the mean, you add all the data together and then divide by the amount of data you have. For example, all the values add up to 225. Divide 225 with the 10 values above and you get 25.5. To find the mode, you find the number that appears the most frequent. In this case, 22 appears 3 times while all the others appear twice or once. So, 22 is the mode. When finding the median, you arrange all the data in increasing order. For example, arranging the data would look like this, 22, 22, 22, 23, 23, 27, 27, 29, 30, and 30. After you arrange the values, you find the middle number. We have 10 values, so we need to pick out the two numbers that are in the middle, which are bolded up above. Add those together and then divide the value by two, which is 25. If we had 9 or 11 values, we'd only need to pick the one that is in the middle, since they're both odd numbers.
Hope this helps! :)
Suppose you conduct one experiment and find that the e = mc3, rather than the historically accepted formula, e = mc2. what should you do next?
Answers
We will repeat the exact same procedure. Something may have gone wrong.
The special theory of relativity by German-born scientist Albert Einstein contains the equation \(E=mc^{2}\), which conveys the idea that mass and energy are one and the same physical substance and may be transformed into one another. The kinetic energy (E) of a body is equal to its increased relativistic mass (m) multiplied by the square root of the speed of light.
Because the mass and the speed of light are both constants, we are unable to test a new variable. Since our findings don't match the accepted formula, we cannot share them.
The result obtained is wrong we cannot apply it to another experiment. The only way we can find the correct result is by repeating the experiment. Because something may have gone wrong on the first attempt.
Therefore, the correct answer is
d) Repeat the exact same procedure.
Read more on Mass energy equivalence:
https://brainly.com/question/32128556
#SPJ4
The correct question is: Suppose you conduct one experiment and find that the \(E=mc^{3}\), rather than the historically accepted formula, \(E=mc^{2}\). What should you do next?
a.Test a new variable
b.Share your findings
c.Apply your results to a new experiment
d.Repeat the exact same procedure
A jacket usually sells for $66.00. If the jacket is 40% off, and sales tax is 6%, what is the total price of the jacket, including tax?
Answers
Answer:
44.22
Step-by-step explanation:
100%-> 66
60%->39.60=
7%->4.62
4.62+39.60=44.22
(b) What is 35% of 60?
Answers
Answer:
21
Step-by-step explanation:
its just... 21 its pretty simple
Here’s how to solve it:
Convert the percent into a decimal by moving the decimal 2 places to the left.
Then multiply the decimal (.35) by 60 and you get your answer
21 !
Select all statements that are true about the triangles.
Figure ABCD with diagonal BC, sides AB and DC are congruent, angle A is congruent to angle D and sides AC and DB are congruent.
Group of answer choices
Triangles ABC and BCD are congruent by the Angle-Side-Angle Triangle Congruence Theorem.
Triangles ABC and DCB are congruent by the Angle-Angle Triangle Congruence Theorem.
Triangles ABC and DCB are congruent by the Side-Side-Side Triangle Congruence Theorem.
Triangles ABC and DCB are congruent by the Side-Angle-Side Triangle Congruence Theorem.
Triangles ABC and BCD are congruent by the Side-Side-Side Triangle Congruence Theorem.
There is not enough information to determine if the triangles are congruent
Answers
Answer:
Triangle ABC and BCD are congruent by the side side side triangle congruence theorem
the line produced by the equation y = 4x – 5 crosses the vertical axis at y = 5. (True or False)
Answers
It is false that the line produced by the equation y = 4x - 5 crosses the vertical axis at y = -5, not y = 5.
When we talk about crossing the vertical axis, we are referring to the point at which the line intersects the y-axis. The y-axis is the vertical line at x = 0. To find the point at which a line intersects the y-axis, we set x = 0 in the equation of the line and solve for y. In this case, the equation of the line is y = 4x - 5. Setting x = 0, we get y = 4(0) - 5 = -5. So the line produced by this equation intersects the y-axis at y = -5, not y = 5.
To know more about equation,
https://brainly.com/question/31310871
#SPJ11
There are two cameras that take pictures of a traffic intersection. Camera A starts taking pictures at 6 AM and takes a picture every 11 minutes. Camera B starts taking pictures at 7 AM and takes pictures every 7 minutes. Camera A and Camera B take a picture at the same time at four different times before noon. When Camera A and Camera B take their last picture together, how many minutes before noon is it?
Answers
Answer:
41 minutes before noon
Step-by-step explanation:
The given parameters are;
The time camera A starts taking pictures = 6 AM
The frequency of picture taking by camera A = Once every 11 minutes
The time camera B starts taking pictures = 7 AM
The frequency of picture taking by camera B = Once every 7 minutes
The number of times both cameras take a picture at the same time before noon = 4 times
Let the time the two cameras first take a picture the same time be x, we have;
11·y - 60 = x
7·z = x
Taking the number of times after 7 camera A snaps and noting that the first snap is 6 minutes after 7, we have
11·b + 6 = x
7·z = x
x is a factor of 7 and 11·b + 6 and x is some minutes after 7
By using Excel, to create a series of values for Camera A based, on 11·b + 6, and dividing the results by 7 we have the factors of 7 at;
28, 105, 182, and 259 minutes after 7
Given that there are 60 minutes in one hour, we have;
259/60 = 4 hours 19 minutes, which is 11:19 a.m. or 41 minutes before noon.
The goal of this project is to apply combinations and permutations to determine the number of possibilities of various scenarios.
1. (10 pts) Define combination and permutation, and provide the formulas for both.
2. Here is a real-life example of a combination and a permutation. I love ice cream and one of my favorite shops has 31 flavors. I can either get a 3-scoop bowl or a 3-scoop cone.

Answers
Combination refers to a way of grouping the elements of a set into a subset in an undered form whereas Permutation is a way of grouping the elements of a set into a subset in an ordered form.
The formula for combination is: C(n,q) = n!/[q !(n-q)!]
The formula for permutation is: P(n,q) = n!/(n-q)!
Real life and specific examplesA real life example of permutation involves selecting 10 people to join a group where they are assigned different duties and a real life example of permutation is selecting 10 people to join a group where they are assigned duties on a first come first served basis.
A specific example of combination is this: In a collection of 17 individuals, 7 $2 cards will be given. In how many ways can the cards be shared? This is combination because there is no set order.
A specific example of permutation is this: In a competition, three individuals contest. In how many ways can they have the 1st, 2nd, and 3rd positions?
Learn more about permutations here:
https://brainly.com/question/1216161
#SPJ1
For the following two numbers, find two factors of the first number such that their product is the first number and their sum is the second number. 32,-12
Answers
By using the unitary method and solving the equations based on the given conditions, we found that the two factors of 32 whose product is 32 and sum is -12 are (-8, -4) and (-4, -8).
Let's assume the two factors we are looking for are a and b. We can write the following equations based on the given conditions:
Equation 1: a * b = 32
Equation 2: a + b = -12
Now, we can use the unitary method to find the values of a and b. Let's start by solving Equation 2 for one variable:
a + b = -12
b = -12 - a
Now substitute this expression for b in Equation 1:
a * (-12 - a) = 32
Expanding the equation:
-12a - a² = 32
Rearranging the equation:
a² + 12a + 32 = 0
We now have a quadratic equation in terms of 'a'. We can solve this equation by factoring or using the quadratic formula. In this case, the equation can be factored as:
(a + 8)(a + 4) = 0
Setting each factor equal to zero:
a + 8 = 0 or a + 4 = 0
Solving for 'a', we have:
a = -8 or a = -4
Now that we have two possible values for 'a', we can substitute them back into Equation 2 to find the corresponding values of 'b':
For a = -8:
b = -12 - (-8)
b = -12 + 8
b = -4
For a = -4:
b = -12 - (-4)
b = -12 + 4
b = -8
Therefore, the two pairs of factors that satisfy the given conditions are (a = -8, b = -4) and (a = -4, b = -8).
To know more about unitary method here
https://brainly.com/question/28276953
#SPJ4
Evaluate the Integral by interpreting it in terms of areas.
0
∫ (3 + √9-x^2) dx = -2
Answers
The given equation states that this integral is equal to -2. However, this is not correct, as the integral represents the sum of the areas and should result in a positive value.
To evaluate the integral in terms of areas, we need to interpret it as the area under a curve. The integrand, 3 + √9-x^2, is the equation of a semi-circle with radius 3 and center at the origin.
Thus, we can interpret the integral as the area of this semi-circle from x = 0 to x = 3. We know that the area of a semi-circle with radius r is (1/2)πr^2, so the area of this semi-circle is (1/2)π(3)^2 = (9/2)π.
However, the integral is evaluated from x = 0 to x = 3, so we need to take half of the area to get the area under the curve from x = 0 to x = 3. Therefore, the area under the curve is (9/4)π.
We also know that the integral is equal to -2, so we can set the area equal to -2:
(9/4)π = -2
Solving for π, we get:
π = (-8/9)
This is not a possible value for π, so there must be an error in the problem statement or the solution method.
To evaluate the integral by interpreting it in terms of areas, follow these steps:
Step 1: Identify the given integral
0 ∫ (3 + √9-x^2) dx
Step 2: Break the integral into two parts
0 ∫ 3 dx + 0 ∫ √(9-x^2) dx
Step 3: Evaluate the first integral (0 ∫ 3 dx)
This represents the area of a rectangle with height 3 and width from 0 to x.
Integral = 3x
Step 4: Evaluate the second integral (0 ∫ √(9-x^2) dx)
This represents the area of a quarter-circle with radius 3 (because 9 = 3^2). The area of the quarter-circle can be found using the formula for the area of a circle (A = πr^2) divided by 4:
Integral = (1/4)π(3)^2 = (9/4)π
Step 5: Add the two integrals together
(3x) + (9/4)π
Step 6: Evaluate the integral at the given limits (0 to x)
At x=0, the integral is 0.
So the definite integral = (3x) + (9/4)π - 0
Learn more about integral at: brainly.com/question/31433890
#SPJ11
You are required to determine the relationship between Gibbs-Duhem equation and the activity coefficient of a selected binary chemical mixture (chemical A and chemical B ) in chemical industrial process. The following model is represented the excess Gibbs energy for the selected binary chemical mixture (chemical A and chemical B ). RT
G E
=X 1
lnγ 1
+X 2
lnγ 2
The Gibbs-Duhem equation says that, in a mixture, the activity coefficients of the individual components are not independent of one another but are related by a differential equation. In a binary mixture the Gibbs-Duhem relation is; x 1
( ∂x 1
∂lnγ i
) T,P
=x 2
( ∂x 2
∂lnγ 2
) T,P
Answers
The Gibbs-Duhem equation relates the activity coefficients of the individual components in a mixture. It states that the activity coefficients are not independent of each other but are related by a differential equation.
In the case of a binary mixture (chemical A and chemical B), the Gibbs-Duhem relation can be written as:
x1 * (∂x1/∂lnγ1)T,P = x2 * (∂x2/∂lnγ2)T,P
Here, x1 and x2 represent the mole fractions of chemical A and chemical B, respectively. The activity coefficients for chemical A and chemical B are denoted as γ1 and γ2, respectively.
The equation shows that the change in mole fraction of one component (x1) with respect to the change in the logarithm of its activity coefficient (lnγ1) is proportional to the change in mole fraction of the other component (x2) with respect to the change in the logarithm of its activity coefficient (lnγ2).
This relationship helps us understand how changes in the activity coefficients of the components affect each other in a binary mixture. By studying this relationship, we can gain insights into the behavior of the mixture and make predictions about its properties.
For example, let's consider a mixture of ethanol (chemical A) and water (chemical B). If the activity coefficient of ethanol (γ1) decreases, the Gibbs-Duhem equation tells us that the mole fraction of ethanol (x1) will also decrease. Similarly, if the activity coefficient of water (γ2) increases, the mole fraction of water (x2) will increase.
Know more about Gibbs-Duhem equation:
https://brainly.com/question/33619595
#SPJ11
help please and fast bc it’s timed :)

Answers
Answer:
x value
Step-by-step explanation:
Suppose that f(1) = 1, f(4) = 5, f '(1) = 3, f '(4) = 3, and f '' is continuous. find the value of 4 1 xf ''(x) dx.
Answers
Answer: b
Step-by-step explanation:
I think
someone help me with number 5 please

Answers
Answer:
The midpoint is (1,2)
Step-by-step explanation:
X1 + Y1/2 , X2+Y2/2
-1+3/2 , 6-2/2
2/2 , 4/2(simplify)
1 , 2
the lendght of an arc intercepted by a cental angle in 6 pi the radios of the circle is 34 . find the measure of the central angle
Answers
The measure of the central angle is 3π/17 radians.
L = rθ
where L is the length of the arc, r is the radius of the circle, and θ is the measure of the central angle in radians.
The radius of the circle is 34 and the length of the arc intercepted by the central angle is 6π. Substituting these values into the formula, we get:
6π = 34θ
To solve for θ, we can divide both sides by 34:
6π/34 = θ
Simplifying the right side, we get:
3π/17 = θ
The measure of the central angle is 3π/17 radians.
The measure of the central angle, we can use the formula for the length of an arc:
Arc length = Radius × Central angle (in radians)
We are given the arc length (6π) and the radius (34). We can rearrange the formula to solve for the central angle:
Central angle = Arc length / Radius
Central angle = (6π) / 34
Now, divide 6π by 34 to get the measure of the central angle:
Central angle ≈ 0.556π radians
To kbow more about radians visit:-
https://brainly.com/question/28990400
#SPJ11
An airplane climbing at a constant angle relative to the ground has reached an altitude of 4 km.At this point, the plane has traveled a horizontal distance of 14 km.What is the angle at which the airplane is climbing
Answers
The angle at which the airplane is climbing is; 15.95°
What is the rate of change?
Let θ be the angle at which the airplane is climbing.
We are told that it has reached an altitude of 4 km and that the plane has traveled a horizontal distance of 14 km. Thus, we can say that;
Δx = 14 Km
Δy = 4 Km
Now, according to trigonometric ratios, we know that;
tan θ = Δy/Δx
Thus;
tan θ = = 4/14
θ = tan⁻¹(0.2857)
θ = 15.95°
The angle at which the airplane is climbing is; 15.95°
Read more about Rate of change at; https://brainly.com/question/12058098
#SPJ1
What is the value of x in the figure below?
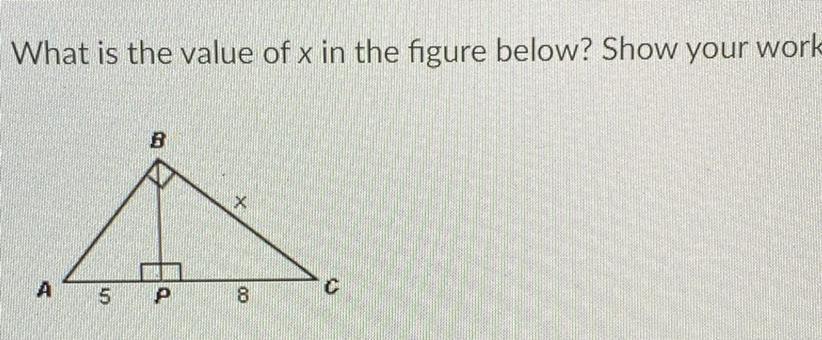
Answers
The value of x in the right triangle is 10.2 units.
How to find the side of a right triangle?A right angle triangle is a triangle that has one of its angles as 90 degrees.
The sum of angles in a triangle is 180 degrees.
The triangles are similar. Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other.
Let's use the similarity to find x as follows:
8 / x = x / 5 + 8
8 / x = x / 13
cross multiply
x² = 13 × 8
x² = 104
square root both sides
x = √104
x = 10.1980390272
x ≈ 10.2 units
learn more on right triangle here: https://brainly.com/question/20399064
#SPJ1
f(x1, x2) 421 +222 3x² +213 5x11² (√₁+√₂)² 10ln(₁) (x₁+x₂)(x² + x3) min(3r1, 10√2) max{5x1,2r2} MP1(x1, x₂) MP2(X1, X₂) TRS(x1, x₂) Output (2,4)
Answers
The given mathematical expression is evaluated for the input values (2, 4). The result of the expression is calculated using various operations such as addition, multiplication, square root, natural logarithm, minimum, maximum, and function composition.
The expression f(x1, x2) involves several mathematical operations. Let's evaluate each part of the expression step by step:
1. The first term is 421 + 222, which equals 643.
2. The second term is 3x² + 213. Plugging in x1 = 2 and x2 = 4, we get 3(2)² + 213 = 3(4) + 213 = 12 + 213 = 225.
3. The third term is 5x11². Substituting x1 = 2 and x2 = 4, we have 5(2)(11)² = 5(2)(121) = 1210.
4. The fourth term is (√₁+√₂)². Replacing x1 = 2 and x2 = 4, we obtain (√2 + √4)² = (1 + 2)² = 3² = 9.
5. The fifth term is 10ln(₁). Plugging in x1 = 2, we have 10ln(2) = 10 * 0.69314718 ≈ 6.9314718.
6. The sixth term is (x₁+x₂)(x² + x3). Substituting x1 = 2 and x2 = 4, we get (2 + 4)(2² + 4³) = 6(4 + 64) = 6(68) = 408.
7. The seventh term is min(3r1, 10√2). As we don't have the value of r1, we cannot determine the minimum between 3r1 and 10√2.
8. The eighth term is max{5x1,2r2}. Since we don't know the value of r2, we cannot find the maximum between 5x1 and 2r2.
9. Finally, we have MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2), which are not defined or given.
Considering the given expression, the evaluated terms for the input values (2, 4) are as follows:
- 421 + 222 = 643
- 3x² + 213 = 225
- 5x11² = 1210
- (√₁+√₂)² = 9
- 10ln(₁) ≈ 6.9314718
- (x₁+x₂)(x² + x3) = 408
The terms involving min() and max() cannot be calculated without knowing the values of r1 and r2, respectively. Additionally, MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2) are not defined.
To learn more about logarithm click here: brainly.com/question/30226560
#SPJ11
Write the quadratic function in vertex form. Then identify the vertex. y=x^2-4x-1
Answers
Answer:
see explanation
Step-by-step explanation:
the equation of a quadratic in vertex form is
y = a(x - h)² + k
where (h, k ) are the coordinates of the vertex and a is a multiplier
y = x² - 4x - 1
using the method of completing the square
add/subtract ( half the coefficient of the x- term)² to x² - 4x
y = x² + 2(-2)x + 4 - 4 - 1
y = (x - 2)² - 5
with vertex = (2, - 5 )
Which of the following is a polynomial?

Answers
Answer:
A poly nomial is an expression with more than one term.
Step-by-step explanation:
Terms are separated by +'s and -'s. So, anything that has multiple terms and are polynomials(poly: the greek root for many.)
If an expression has a division, and the denominator(the number under) is a variable(x,y,z, etc.), then it is not a monomial. Thus it is a polynomial.
So to sort of answer your question if you're one of those people who just look to the bottom for answers to be lazy, I see 3 polynomials.
Pleaseee help please I need itt!

Answers
The volume of the cuboids is given by the product of their dimensions.
What is cuboid?A cuboid is a three-dimensional shape that has 6 faces, 12 edges, and 8 vertices.
Given are cuboids, we need to determine the height, width and length of these,
To find the same, we just have to count the number of cubes, and the volume is the product of dimension,
1) Height = 3 units
Width = 4 units
Length = 4 units
Volume = 48 units³
2) Height = 5 units
Width = 2 units
Length = 5 units
Volume = 20 units³
3) Height = 3 units
Width = 5 units
Length = 5 units
Volume = 75 units³
4) Height = 4 units
Width = 3 units
Length = 5 units
Volume = 60 units³
5) Height = 4 units
Width = 5 units
Length = 3 units
Volume = 60 units³
6) Height = 3 units
Width = 5 units
Length = 5 units
Volume = 75 units³
7) Height = 2 units
Width = 2 units
Length = 3 units
Volume = 12 units³
8) Height = 5 units
Width = 3 units
Length = 5 units
Volume = 75 units³
9) Height = 5 units
Width = 2 units
Length = 5 units
Volume = 50 units³
10) Height = 4 units
Width = 4 units
Length = 4 units
Volume = 64 units³
Learn more about cuboids, click;
https://brainly.com/question/29568631
#SPJ1
Divide 1 m 71 cm in the ratio of 12:7
Answers
Answer:
Total length= 171 cm
Required ratio= 11:8
Let 11x and 8x be the required lengths.
Then, 11x+8x=171
19x=171
x=9
Therefore, required lengths are 11x=99
and 8x=72.
5a) Determine the measure of each unknown angle

Answers
Answer:
Step-by-step explanation:
25, i think
Pleaze help worth 30 points

Answers
Answer:
the second one
Step-by-step explanation:
Each number moves up the same amount each time, on the table. For both x and y.