Answers
Answer:
What's the question?
Step-by-step explanation:
Related Questions
Find x. (I'm so bad with circles pls help)

Answers
================================================
Explanation:
x = radius of the circle
The vertical leg of the right triangle is also x. The horizontal leg is 99.
The hypotenuse is x+81
We have these triangle side lengths:
a = xb = 99c = x+81Use the pythagorean theorem to tie them all together, which will allow us to solve for x.
\(a^2+b^2 = c^2\\\\\text{x}^2+99^2 = (\text{x}+81)^2\\\\\text{x}^2+9801 = \text{x}^2+162\text{x}+6561\\\\9801 = 162\text{x}+6561\\\\9801-6561 = 162\text{x}\\\\3240 = 162\text{x}\\\\\text{x} = 3240/162\\\\\text{x} = 20\)
A tool like GeoGebra or WolframAlpha can be used to confirm the answer is correct.
I will mark 1st correct answer as brainliest
Let f(x) = log base 3 of x and g(x) = 3^x.
What is the value of
[f(g(f(f(f(g(27))))))?]
I will mark 1st correct answer as brainliest
Answers
The value of the composite function [f(g(f(f(f(g(27))))))], when f(x) = log₃(x) and g(x) = 3ˣ is 1
How to evaluate the composite functionFrom the question, we have the following parameters that can be used in our computation:
Let f(x) = log base 3 of x and g(x) = 3^x.
Express the equations properly
So, we have the following representations
f(x) = log₃(x) and g(x) = 3ˣ
Calculating the composite function [f(g(f(f(f(g(27))))))], we have
[f(g(f(f(f(g(27))))))] = [f(g(f(f(f(3²⁷))))))]
Next, we have:
[f(g(f(f(f(g(27))))))] = [f(g(f(f(log₃(3²⁷))))))]
This gives
[f(g(f(f(f(g(27))))))] = [f(g(f(f(27))))))]
For f(27), we have
[f(g(f(f(f(g(27))))))] = [f(g(f(3)))))]
For f(3), we have
[f(g(f(f(f(g(27))))))] = [f(g(1))))]
Calculating g(1), we have
[f(g(f(f(f(g(27))))))] = f(3)
Lastly, we have
[f(g(f(f(f(g(27))))))] = log₃(3)
Evaluate
[f(g(f(f(f(g(27))))))] = 1
Hence, the solution is 1
Read more about composite function at
https://brainly.com/question/26044179
#SPJ1
Austin walked 3 km from his house to park a he then walked another 4 km from park a to park b the total time taken was 84 min find Austin’s average speed
Answers
Austin's average speed was 5 km / hour.
To find Austin's average speed, we need to divide the total distance he covered by the total time taken.
The distance Austin covered is the sum of the distances he walked from his house to Park A (3 km) and from Park A to Park B (4 km), which gives a total distance of 7 km.
The total time taken is 84 minutes which is equivalent to 1.4 hours.. Therefore the average speed at which Austin walked is:
Average speed = Total distance covered/Total time taken Average speed = 7 km/1.4 hours Average speed = 5 km/hourSo the correct answer is that Austin's average speed was 5 km/hour.
Learn more about average speed brainly.com/question/4931057
#SPJ4
Is 8.33865 irrational or rational
Answers
Answer:
Irrational
Step-by-step explanation:
A rational number can be made by dividing two integers, thereby, 8.33865 is an irrational number.
Hope this helps!
A firm manufactures padded shipping bags. A cardboard carton should contain 100 bags, but machine operators fill the cardboard cartons by eye, so a carton may contain anywhere from 98 to 123 bags (average = 105.5 bags). Each padded bag costs $0.03. Management realizes that they are giving away 5(1/2)% of their output by overfilling the cartons. One solution is to automate the filling of shipping cartons. This should reduce the average quantity of bags per carton to 100.3, with almost no cartons containing fewer than 100 bags. The equipment would cost $18,600 and straight-line depreciation with a 10-year depreciable life and a $3600 salvage value would be used. The equipment costs $16,000 annually to operate. 200,000 cartons will be filled each year. This large profitable corporation has a 40% combined federal-plus-state incremental tax rate. Assume a 10-year study period for the analysis and an after-tax MARR of 15%. Compute: (a) The after-tax present worth (b) The after-tax internal rate of return (c) The after-tax simple payback period =1.9 years
Answers
The after-tax present worth according to the given values is $732,140.56 and the internal rate of return is 22.65%.
(a) To compute the after-tax present worth, we need to determine the net cash flow for each year and discount it to present value using the after-tax MARR of 15%.
Year 0: Initial cost of equipment = -$18,600
Years 1-10:
Revenue from bags = (100.3 bags/carton) x ($0.03/bag) x (200,000 cartons/year) = $120,780
Cost savings from reducing overfilling = (5.5%) x ($0.03/bag) x (200,000 cartons/year) = $3,300
Operating cost of equipment = -$16,000
Depreciation expense = -$1,800 (($18,600 - $3,600 salvage value) / 10 years)
Net cash flow for each year:
Year 0: -$18,600
Year 1: $107,280 ($120,780 + $3,300 - $16,000 - $1,800)
Year 2: $109,160 ($120,780 + $3,300 - $16,000 - $1,800)
...
Year 10: $113,640 ($120,780 + $3,300 - $16,000 - $1,800)
Discounting each year's net cash flow to present value and summing them up, we get:
PV = -$18,600 + ($107,280 / (1+0.15)^1) + ($109,160 / (1+0.15)^2) + ... + ($113,640 / (1+0.15)^10)
PV = -$18,600 + $750,740.56
PV = $732,140.56
Therefore, the after-tax present worth is $732,140.56.
(b) To compute the after-tax internal rate of return, we need to find the discount rate that makes the net present value equal to zero. We can use trial and error or a financial calculator to solve this.
Using trial and error, we find that a discount rate of approximately 22.65% makes the net present value equal to zero. Therefore, the after-tax internal rate of return is approximately 22.65%.
(c) To compute the after-tax simple payback period, we need to determine how long it takes for the cumulative net cash flow to equal the initial cost of the equipment.
Year 0: -$18,600
Year 1: $107,280
Year 2: $109,160
Year 3: $110,960
Year 4: $112,680
Year 5: $114,320
Year 6: $115,880
Year 7: $117,360
Year 8: $118,760
Year 9: $120,080
Year 10: $121,320
The cumulative net cash flow becomes positive in year 3, so the after-tax simple payback period is approximately 1.9 years (between year 2 and year 3).
To learn more about After-tax, visit:
https://brainly.com/question/25790997
#SPJ11
Which of the following will cause a logical error if you are attempting to compare x to 5?
Answers:
a. if (x >= 5)
b. if (x = 5)
c. if (x == 5)
d. if (x <= 5)
Answers
Logical Error: In computer programming language, a logic error is a bug or in a program or code that causes it to operate incorrectly, but not to terminate abnormally (or crash).
A logic error developed unintended or undesired output or other behavior, although it may not immediately be recognized as such.
For example, assigning a value to the wrong variable may cause a many of unexpected program errors.
These errors can be programmer mistakes or sometimes machine less memory to load the code.
if(x>=5) {
// program
}
else if(x==5) {
//program
}
else(x<=5) {
//program
}
they all do not give any error.
x=5 gave an error because it is value assigning to 5.
To know more about Logical Error:
https://brainly.com/question/28957248
#SPJ
Solve this for brainliest
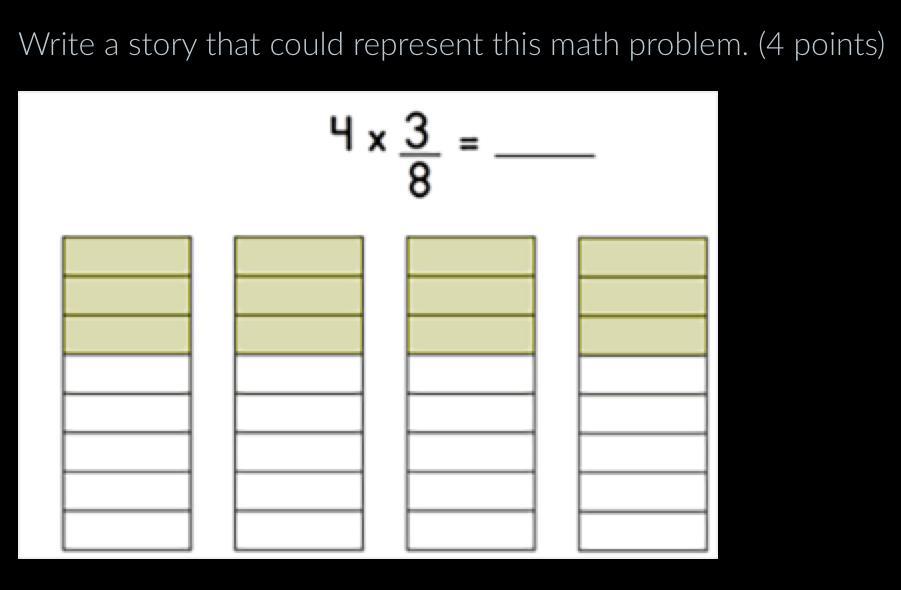
Answers
4 x 3/8 = 3/2 = 1 1/2 =1.5
I hope this helps!!
Find the Volume
If its correct i give 5 stars a like and brainliest

Answers
Answer:
171 in³
Step-by-step explanation:
Simplify
(2a2b4z)(6a3b225)
Answers
Answer:
64800a²b²z
Step-by-step explanation:
use a calculator
Find f(2) and f(3).
f(1) = 3
f(n) = 7f(n = 1)
Answers
Answer:
do it got a picture
on the edge2020
Step-by-step explanation:
Solve the system of equations -x+10y-2z=8. y-52=-4, 1+3x-y=0 via the SOR method using the starting point xo=0,yo=0.9,zo=1.1 tolerance=tol=0.05,a11=3,a22=10,a33=5and=0.9. [16 marks]
Answers
Three iterations are performed here to solve the system of equations using the Successive Over-Relaxation (SOR) method.
To solve the system of equations using the Successive Over-Relaxation (SOR) method, we need to iterate through the equations until convergence is achieved within the given tolerance.
The system of equations is:
- x + 10y - 2z = 8 (Equation 1)
y - 52 = -4 (Equation 2)
1 + 3x - y = 0 (Equation 3)
We start with the initial guesses:
x₀ = 0
y₀ = 0.9
z₀ = 1.1
Using the SOR method, the iteration formula is:
xₖ⁺¹ = (1 - ω)xₖ + (ω/a₁₁)(b₁ - a₁₂yₖ - a₁₃zₖ)
yₖ⁺¹ = (1 - ω)yₖ + (ω/a₂₂)(b₂ - a₂₁xₖ - a₂₃zₖ)
zₖ⁺¹ = (1 - ω)zₖ + (ω/a₃₃)(b₃ - a₃₁xₖ - a₃₂yₖ)
where ω is the relaxation factor, a₁₁, a₂₂, and a₃₃ are the diagonal elements of the coefficient matrix, b₁, b₂, and b₃ are the right-hand side values, and the subscripts k and k+1 represent the iteration steps.
Given:
tol = 0.05 (tolerance)
a₁₁ = 3
a₂₂ = 10
a₃₃ = 5
ω = 0.9
Let's proceed with the calculations using the SOR method:
Iteration 1:
x₁ = (1 - 0.9)(0) + (0.9/3)(8 - 10(0.9) - 2(1.1)) = 0.6
y₁ = (1 - 0.9)(0.9) + (0.9/10)(-4 - 3(0) - 5(1.1)) = 0.833
z₁ = (1 - 0.9)(1.1) + (0.9/5)(1 - 3(0) - 10(0.833)) = 1.035
Iteration 2:
x₂ = (1 - 0.9)(0.6) + (0.9/3)(8 - 10(0.833) - 2(1.035)) = 0.610
y₂ = (1 - 0.9)(0.833) + (0.9/10)(-4 - 3(0.6) - 5(1.035)) = 0.841
z₂ = (1 - 0.9)(1.035) + (0.9/5)(1 - 3(0.6) - 10(0.841)) = 1.012
Iteration 3:
x₃ = (1 - 0.9)(0.610) + (0.9/3)(8 - 10(0.841) - 2(1.012)) = 0.620
y₃ = (1 - 0.9)(0.841) + (0.9/10)(-4 - 3(0.610) - 5(1.012)) = 0.842
z₃ = (1 - 0.9)(
1.012) + (0.9/5)(1 - 3(0.610) - 10(0.842)) = 1.008
Continue these iterations until the solution converges within the given tolerance.
To know more about system of equations , refer here:
https://brainly.com/question/20067450
#SPJ4
pls solve cus im not smart
image given

Answers
From the factoring, it is possible to find the following answers:
Letter A: \(\frac{x\left(x+2\right)}{x-3}\)
Letter B: \(-\frac{2x^5}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}\)
Letter C: \(x^2+y^2\)
FactoringIn math, factoring or factorization is used to write an algebraic expression in factors. There are some rules for factorization. One of them is a factor out a common term for example: x²-x= x(x-1), where x is a common term.
Letter aHere you should factor the given expression.
\(\frac{x^3-4x}{x^2-5x+6} \\ \\ \frac{x\left(x+2\right)\left(x-2\right)}{x^2-5x+6}\\ \\ \frac{x\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\\ \\ \frac{x\left(x+2\right)}{x-3}\\ \\ Then,\\ \\ \frac{x^3-4x}{x^2-5x+6} =\frac{x\left(x+2\right)}{x-3}\)
Letter bFirstly, you should replace the variables A, B and C for the given expressions.
\(\frac{1}{1-x+x^2}-\frac{1}{1+x+x^2}-\frac{2x}{1+x^2}\)
After that, you should find the least common multiple.
\(\frac{\left(x^2+1\right)\left(x^2+x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}-\frac{\left(x^2+1\right)\left(x^2-x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}-\frac{2x\left(x^2-x+1\right)\left(x^2+x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}\)
Finally, you can simplify the expression
\(\frac{\left(x^2+1\right)\left(x^2+x+1\right)-\left(x^2+1\right)\left(x^2-x+1\right)-2x\left(x^2-x+1\right)\\ \\ \left(x^2+x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}\\ \\ \frac{-2x^5}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}= -\frac{2x^5}{\left(x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)}\)
Letter cFirstly, you should replace the variables P, Q and R for the given expressions.
\(\frac{x^4-y^4}{x^2+y^2-2xy}\cdot \frac{\left(x+y\right)^2-4xy}{x^3-y^3}\div \frac{x+y}{x^2+y^2+xy}\)
Rewriting
\(\frac{\frac{x^4-y^4}{x^2+y^2-2xy}\cdot \frac{\left(x+y\right)^2-4xy}{x^3-y^3}}{\frac{x+y}{x^2+y^2+xy}}=\frac{\frac{x^4-y^4}{x^2+y^2-2xy}\cdot \frac{\left(x+y\right)^2-4xy}{x^3-y^3}\left(x^2+y^2+xy\right)}{x+y}\\ \\\)
\(\frac{\left(x^2+y^2\right)\left(x+y\right)}{x+y}=x^2+y^2\)
Read more about the factoring here:
brainly.com/question/11579257
#SPJ1
If you double my number, then add 2,
divide by 20 and add -1, the result is 0. What's my number?
Answers
Answer:
77,464.4
Step-by-step explanation:
its right
Answer:
9
Step-by-step explanation:
9 doubled is 18.
18 plus 2 is 20.
20 divided by 20 is 1.
1 plus -1 is 0.
0.0000066 stantdard form or scientific notationn
Answers
Hope this helped:)
Answer:
\( 6.6 \times {10}^{ - 6} \)
Step-by-step explanation:
\(0.0000066 = 6.6 \times {10}^{ - 6} \)
1. (5 points) The arc of a football thrown by Patrick Mahomes is modeled by the equation h=-16t2 + 36t + 6, where h = the height of the ball and t = the time in seconds. Will the ball reach a height of 24 feet?
Answers
In order to determine if the ball reaches the 24 ft, replace h = 24 and solve the quadratic equation. If the solutions are real, then, the ball does reach 24ft.
Proceed as follow:
h = 16t² + 36t + 6
24 = 16t² + 36t + 6
16t² + 36t + 6 - 24 = 0
16t² + 36t - 18 = 0
use he quadratic formula, given by:
\(t=\frac{-b\pm\sqrt[]{b^{2}-4ac}}{2a}\)In this case, a = 16, b = 36 and c = -18
\(\begin{gathered} t=\frac{-36\pm\sqrt[]{(36)^{2}-4(16)(-18)}}{2(16)} \\ t=\frac{-36\pm49.47}{32} \\ t_1=-2.67 \\ t_2=\text{0}.42 \end{gathered}\)negative times do not have physical meanning, then, the available solution is
t = 0.42
Hence, you can conclude that the ball reaches 24 ft for a time of 0.42 seconds.
I just need to know the slope and the y-intercept of the equation, thanks!

Answers
Answer:
Slope is \(\frac{1}{4}\) and intercept is -2.
Step-by-step explanation:
Slope if the multiplied before the x (so \(\frac{1}{4}\)).
Intercept is the standalone number (so -2).
Susan had four bags of candy, each weighing 6 ounces. Isabel had one bag of candy weighing 1 pounds. Which girl has the more candy in weight? Your work will justify your answer.
Answers
Susan has more candy in weight compared to Isabel.
To compare the candy weights between Susan and Isabel, we need to ensure that both weights are in the same unit of measurement. Let's convert Isabel's candy weight to ounces for a fair comparison.
Given:
Susan: 4 bags x 6 ounces/bag = 24 ounces
Isabel: 1 bag x 16 ounces/pound = 16 ounces
Now that both weights are in ounces, we can see that Susan has 24 ounces of candy, while Isabel has 16 ounces of candy. As a result, Susan is heavier on the candy scale than Isabel.
for such more question on weight
https://brainly.com/question/24191825
#SPJ8
Only need help on #20 & #21 answer step by step if u can

Answers
Answer:
Step-by-step explanation: 22
tan30° = \(\frac{12}{x}\) ⇒ \(\frac{\sqrt{3} }{3}\) = \(\frac{12}{x}\) ⇒ x = 12√3
c = √(12√3)² + 12² = 24
P= a+b+c = 12√3 + 12 + 24 = 36+12√3
How long would it take R20000 invested today at a simple interest rate of 9% p.a. to reach an investment goal of R30000.
A Approximately 5.6 years
B Approximately 6.1 years
C Approximately 4.7 years
D Approximately 5.1 years
Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 30000\\ P=\textit{original amount deposited}\dotfill & \$20000\\ r=rate\to 9\%\to \frac{9}{100}\dotfill &0.09\\ t=years \end{cases} \\\\\\ 30000 = 20000[1+(0.09)(t)] \implies \cfrac{30000}{20000}=1+0.09t\implies \cfrac{3}{2}=1+0.09t \\\\\\ \cfrac{3}{2}-1=0.09t\implies \cfrac{1}{2}=0.09t\implies \cfrac{1}{2(0.09)}=t\implies 5.6\approx t\)
What is the rate of change in y per unit change in x for this linear function?
A. -5
B. -2.5
C. -2
D. -0.4

Answers
B. -2.5
Step-by-step explanation:
This is asking for gradient. Pick any two points (x, y) then calculate the y change ÷ x change. example, (0, -5) and (-2, 0). with [0-(-5) ÷ -2-0] you get -2.5
During the next two months Johnson-Perry Company must meet the demands provided in Table 1 for their Yummy brand and Wholesome brand sandwich patties. These demands must be met on time. Max Monthly Total Production 12,000,000 During each month, at most 12 million patties total can be produced. Both Yummy and Wholesome patties can be held in inventory at a cost of $0.05 each per month in a cold storage facility. Storage Cost per Unit S 0.05 TABLE 2 Cost per pound of raw materials Dark Meat Month 1 Cost per Ib Month 2 Cost per lb $0.10 $0.14 $0.15 $0.18 $0.02 $0.03 Table 2 shows the cost per pound of raw material used to produce sandwich patties. Table 3 shows the pounds of raw material required to produce a single patty of each type. Meat and grain gruel can be used only in the month it was purchased. Light Meat Grain Gruel TABLE 3 Raw material required per patty (lbs) Dark Meat Yummy Wholesome Light Meat 1.00 0.00 Grain Gruel 0.00 0.50 0.50 1.00 As shown in Table 4, each Yummy patty produced contains 20 grams of fat and each Wholesome patty contains 8 grams of fat. Each month, the combination of all patties produced by the company must average no more than 13 grams of fat for regulatory reasons. TABLE4 Develop a linear model and properly optimize it with Solver to minimize the total cost of producing and storing Yummy and Wholesome sandwich patties. Non-integer solutions are fine - Do not use any integer constraints. Fat (9) per Patty Yummy Wholesome 20 8 Max Avg Fat (9) of Patties Produced per Month 13
Answers
The optimized values of X and Y will represent the number of Yummy and Wholesome patties produced per month.
The total cost of production and storage will be minimized according to the objective function.
What is linear programming?
Linear programming is a mathematical method used to optimize (maximize or minimize) a linear objective function subject to a set of linear constraints. It is widely used in various fields, including economics, operations research, engineering, and finance, to solve optimization problems.
In linear programming, the objective is to find the best possible solution that satisfies a given set of constraints while optimizing a specific objective. The objective function represents the quantity to be maximized or minimized, such as profit, cost, time, or resource utilization. The constraints define the limitations or restrictions on the decision variables.
Decision Variables:
Let X be the number of Yummy patties produced per month.
Let Y be the number of Wholesome patties produced per month.
Objective Function:
Minimize the total cost of producing and storing Yummy and Wholesome sandwich patties.
Total Cost = (Production Cost per patty * Number of Yummy patties) + (Production Cost per patty * Number of Wholesome patties) + (Storage Cost per patty * Number of Yummy patties) + (Storage Cost per patty * Number of Wholesome patties)
Constraints:
Production capacity constraint: X + Y <= 12,000,000 (the total number of patties produced per month should not exceed 12 million).
Demand constraints: X >= demand for Yummy patties per month
Y >= demand for Wholesome patties per month
Fat content constraint: (20X + 8Y) / (X + Y) <= 13 (average fat content should not exceed 13 grams per patty)
To solve this linear programming problem and optimize the total cost, you can use Solver in software like Microsoft Excel. Here are the steps to set up and solve the problem using Solver:
Set up the spreadsheet:
Create a table with columns for variables (X and Y), objective functions, and constraints.
Enter the appropriate formulas for the objective function and constraints based on the given information.
Define the objective cell as the total cost and set it to minimize.
Set up the Solver:
Open Solver in Excel (usually found under the Data or Analysis tab).
Set the objective cell as the target to minimize.
Define the decision variables and their limits (X and Y >= 0).
Add the constraints based on the given conditions.
Set the Solver options as needed (non-integer solutions are allowed).
Run the Solver:
Click the Solve button to find the optimal solution.
Solver will adjust the values of X and Y to minimize the total cost while satisfying the constraints.
Review the results:
Once Solver completes, review the solution provided.
The optimized values of X and Y will represent the number of Yummy and Wholesome patties produced per month.
The total cost of production and storage will be minimized according to the objective function.
By following these steps and using Solver, you can find the optimal solution for minimizing the total cost of producing and storing Yummy and Wholesome sandwich patties while satisfying the given constraints.
To learn more about linear programming :
https://brainly.in/question/15044395
#SPJ4
(04.02 MC)
The equation of line CD is y = 3x − 3. Write an equation of a line perpendicular to line CD in slope-intercept form that contains point (3, 1).
y = 3x + 0
y = 3x − 8
y = negative 1 over 3x + 2
y = negative 1 over 3x + 0
Answers
Answer:y=negative 1 over 3x +2
Step-by-step explanation:
Answer:vvvvvvvvvvvvvvvvvvvvvvv
Step-by-step explanation: the guy above me is correct
vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv
y = negative 1 over 3x + 2

PICNIC TABLE How do you know that the top of the picnic table is parallel to the ground?

Answers
Answer:
because the lines are parallel meaning they will never cross
Step-by-step explanation:
A shop sells orange juice in the following ways:
500 ml bottle for £1.25
1.5 litre carton for £2.35 each or 2 cartons for £3.50
2 litre carton for £3.25
What's the cheapest way of buying exactly 8 litres with no extra?
Find the amount of each type of bottle or carton you need and the total cost of buying 8 litres
Answers
Answer:
1.
1.5 litre carton for $2.35 is the cheapest way since it's the cheapest out of all the other options.
2.
a. 1.25 / 0.5 = $2.50 per L
2.35 / 1.5 = $1.57 per L
3.25 / 2 = $1.63 per L
b. 2.50 x 8 = $20.00 per 8 L
1.57 x 8 = $12.56 per 8 L
1.63 x 8 = $13.04 per 8 L
Step-by-step explanation:
find unit rate (cost / quantity)
Price of an article is 400 and sold with discount including 13% vat at 339 find discount rate
Answers
To remove 13% vat divide by 1.13
339 / 1.13 = 300 the discounted price.
The amount of discount = 400 - 300 = 100
Discount rate = 100 / 400 = 1/4 = 25%
describe the end behavior of the function using limit notation.(SHOW ALL WORK)

Answers
We will know the end behavior as follows:
\(\lim _{x\rightarrow{\infty}}=x^4-3x^2+2=\lim _{x\rightarrow\infty}x^4+\lim _{x\rightarrow\infty}-3x^2+\lim _{x\rightarrow\infty}2\)\(=\lim _{x\rightarrow\infty}x^4-3\lim _{x\rightarrow\infty}x^2+\lim _{x\rightarrow\infty}2=\infty-3(\infty)+2=\infty\)\(\Rightarrow\lim _{x\rightarrow\infty}x^4-3x^2+2=\infty\)Please i need help please i need it quickly
Answers
Leo plans to go to the arcade with his friend. His parents gave him $20 to spend. He wants to buy a soda and bag of hot Cheetos which will be $4.25. If each game cost $0.75, how many games can he play? A. Write an inequality to solve this situation. B. Solve the inequality to answer games Leo can play C. Explain how you solved the inequality.
Answers
0.75x + 4.25 ≤ 20
B. To solve the inequality:
0.75x ≤ 20 - 4.25
0.75x ≤ 15.75
x ≤ 21
Leo can play a maximum of 21 games.
C. The inequality represents the maximum amount of money Leo can spend on games and snacks, which is $20. The left side of the inequality represents the total amount of money spent on games and snacks, and it must be less than or equal to $20. We solve for x, which represents the number of games Leo can play within the $20 budget. The solution is x ≤ 21, meaning Leo can play a maximum of 21 games.
Pleaseee answer correctly !!!!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!!!

Answers
Answer:
OS is congruent to SQ
Step-by-step explanation:
Above is the question

Answers
Answer:
its A
Step-by-step explanation:
asymptotes:=-1 and hole:x=4
