Do the expressions (-2)(3) and (2)(-3) have the same value? Show your thinking .
Answers
(-x)(y) = -xy
(x)(-y) = -xy
Until this happens:
(-x)(-y) = xy

Related Questions
The scores of an eighth-grade math test have a normal distribution with a mean u = 83 and a standard deviation o = 5. If
Din's test score was 92, which expression would she write to find the z-score of her test score?
OZ. z=92-83/83
z=83-91/5
z=92-83/5
z=5-83/92
Answers
Answer:
z=92-83/5
Step-by-step explanation:
The formula for calculating a z-score is given as:
z = (x-μ)/σ,
where
x is the raw score
μ is the population mean
σ is the population standard deviation.
Where: from the question
x is the raw score = 92
μ is the population mean = 83
σ is the population standard deviation = 5
z = 92 - 83/5
Therefore, expression would she write to find the z-score of her test score is
z = 92 - 83/5
Answer:
C on EDG
Step-by-step explanation:
The chart shows the distances, in miles, between some towns and cities.
Wrexham
12
21
15
Mold
20
COR
27
RUTHIN
Corwen
23
OSWESTRY
Oswestry
Darren lives in Wrexham and works in Corwen.
a) Use the chart to find the road distance
between Wrexham and Corwen.
Elyas lives in Mold and works in Oswestry for
5 days a week. Each day he travels to and from
work using the route shown on the map.
b) How many miles, in total, does he travel to
and from work each week?

Answers
The road distance between Wrexham and Corwen can be found to be 21 miles
The miles in total that Elyas travelled to and from work each week would be 270 miles.
How to find the road distance and miles traveled ?The road distance between Wrexham and Corwen can be found at the intersection between Wrexham and Corwen on the table which is 21 miles.
The miles between Mold and Oswestry by the same method would be 27 miles. This means that the total miles traveled by Elyas :
= 27 miles x 2 going and coming x 5 days a week
= 270 miles
Find out more on road distance at https://brainly.com/question/29085711
#SPJ1
(please help!) Find the surface area of the prism.

Answers
Answer:
42 sq ft
Step-by-step explanation:
L x W x H
3 x 7 x 2
21 x 2
42 sq ft
Autumn and her children went into a bakery and she bought $5 worth of donuts and cookies. Each donut costs $1 and each cookie costs $0.50. She bought a total of 6 donuts and cookies altogether. Graphically solve a system of equations in order to determine the number of donuts, x, and the number of cookies, y, that Autumn bought.
Answers
Autumn bought 4 Donuts and 2 Cookies worth of 5 dollars.
What are simultaneous equations?We know two simultaneous equations have a unique solution when they intersect at a point,
when they are parallel they have no solution and when they are coinciding they have an infinite no. of solutions.
Given, Autumn and her children went into a bakery and she bought $5 worth of donuts and cookies.
Each donut costs $1 and each cookie costs $0.50. She bought a total of 6 donuts and cookies altogether.
Let us denote no. of Donuts by x and no. of Cookies by y.
∴ x + y = 6...(i) and x + 0.5y = 5...(ii).
Subtracting eqn(ii) from eqn(i) we get y = 2 and substituting the value of y in eqn(i) we get x = 4.
Autumn bought 4 Donuts and 2 cookies with 5 dollars.
learn more about simultaneous equations here :
https://brainly.com/question/24065247
#SPJ1

Absco, Inc. purchased a framing machine for $60,000 on January 1, 2021. The machine is expected to have a four- year life, with a residual value of $5,000 at the end of four years. Using the straight-line method, depreciation for 2021 and book value at December 31, 2021, would be: $13,750 and $41,250 respectively. $13,750 and $46,250 respectively. $15,000 and $45,000 respectively. $15.000 and $40.000
Answers
Depreciation for 2021 and book value at December 31, 2021, would be: $13,750 and $46,250 respectively. The correct answer is B.
To calculate the depreciation for 2021 using the straight-line method, we need to determine the depreciable cost and divide it by the expected life of the machine.
Given:
Purchase cost of the machine = $60,000
Residual value at the end of four years = $5,000
Expected life of the machine = four years
Depreciable cost = Purchase cost - Residual value
Depreciable cost = $60,000 - $5,000
Depreciable cost = $55,000
Depreciation per year = Depreciable cost / Expected life
Depreciation per year = $55,000 / 4
Depreciation per year = $13,750
Therefore, the depreciation for 2021 using the straight-line method is $13,750.
To calculate the book value at December 31, 2021, we subtract the accumulated depreciation from the initial cost of the machine:
Book value = Purchase cost - Accumulated depreciation
Since it is the first year, the accumulated depreciation would be equal to the depreciation for 2021.
Book value = $60,000 - $13,750
Book value = $46,250
Therefore, the book value at December 31, 2021, is $46,250.
So, the correct option is B
Learn more about depreciation at https://brainly.com/question/16356562
#SPJ11
SOMEONE HELP ME PLEASE

Answers
Answer:
c = 180
Step-by-step explanation:
Varies joint with d and the square of g
c = k d g^2 where k is a constant
30 = k * 15 * 2^2
30 = 60k
30/60 = k
1/2 = k
c = 1/2 d g^2
Let d = 40 and g=3
c = 1/2 ( 40) (30^2
c = 20 (9)
c = 180
Find the coordinates of the midpoint of MN with endpoints M(-2,6) and N(8,0).
(3,2)
(1,0)
(8,0)
(3,3)
Answers
Answer:
(3, 3)
Step-by-step explanation:
Use the midpoint formula (x1+x2/2, y1+y2/2)
so its (-2+8/2, 6+0/2)
which is (3,3)
Grant plans to evaporate enough water from 22 gallons of a 16% ammonia solution to make a 24% ammonia solution. Which equation can he use to find n, the number of gallons of water he should remove?
3.52 (22 minus n) = 0.24
StartFraction 22 minus n Over 3.52 EndFraction = StartFraction 24 Over 100 EndFraction
StartFraction 3.52 Over 22 minus n EndFraction = StartFraction 24 Over 100 EndFraction
3.52 + (22 minus n) = 0.24
Answers
The equation that he used to find n, the number of gallons of water he should remove is 3.52 / (22 - n) = 24 / 100. Option C is correct.
Functions are the relationship between sets of values. e g y=f(x), for every value of x there is its exists in a set of y. x is the independent variable while Y is the dependent variable.
Amount of ammonia in the solution 16% x 22 gallons = 3.52 gallons
The proportion of ammonia remains the same as the water evaporates, but the total composition of the solution is decreased by the amount of water that evaporates.
Quantity of ammonia = 3.52 gallons
Quantity of water after evaporation = 22 - n
Composition of ammonia after evaporation of water, 24% = 24/100
Now the percentage of ammonia after evaporates
Quantity of ammonia / Remaining water = 24%
3.52 / (22 - n) = 24 / 100
Thus, the equation that he used to find n, the number of gallons of water he should remove is 3.52 / (22 - n) = 24 / 100.
Learn more about function here:
brainly.com/question/21145944
#SPJ1
recall that in problem 3 of the reading questions for section 2.1, you found that if , then . use this to find a formula for the tangent line to at .
Answers
The tangent line is y=x-1 and differentiation of ln(x) is 1/x
What does differentiation in mathematics mean?
Differentiation is a technique for determining a function's derivative. In mathematics, the technique of differentiation is used to determine the instantaneous rate of change in a function dependent on one of its variables.
The most prevalent example is velocity, which is the rate at which a distance changes in relation to time.
The ratio of the vertical to the horizontal distance between any two points on it is called slope of ray or line or line segment in analytical geometry.
y-y1 = m(x-x1)
If the function passes through (1,0) and the slope equals to 1 is:
y-0 = 1(x-1)
y=x-1
Learn more about differentiation
brainly.com/question/24898810
#SPJ4
The complete question is -
Recall that in Problem 3 of the reading questions for Section 2.1, you found that if f(x) = ln(x), then f'(2) = 1/2. Use this to find a formula for the tangent line to f(x) = ln(x) at x = 2.
Solve for x to the nearest 10 th. 65 = 690(0.5)^x/13
Answers
Answer:
x=−0.292355
Step-by-step explanation:
The box-and-whisker plot below
shows the test scores for the last
quiz. What is the interquartile range?
IS
40
50
60
70
80
90
100
Answers
Answer:
Interquartile range = 40
Step-by-step explanation:
interquartile range = Q3-Q1
It has 7 numbers, in order to make it even we remove the middle number (70) to make two sets of quartiles
Q1 = 50 (middle of the lower quartile)
Q3= 90 (middle of the higher quartile)
a garden table and a bench cost 573 combined. The garden table costs 77.00 less than the bench. what is the cost of the bench
Answers
Let 'x' represent the cost of the garden table.
Let 'y' represent the cost of the bench.
Therefore, from the first statemenet
\(x+y=573\ldots\ldots.1\)From the second statement,
\(x=y-77\ldots\ldots2\)Substitute x = y - 77 into equation 1
\(\begin{gathered} x+y=573 \\ y-77+y=573 \end{gathered}\)Collect like terms
\(\begin{gathered} y+y=573+77 \\ 2y=650 \end{gathered}\)Divide both sides by 2
\(\begin{gathered} \frac{2y}{2}=\frac{650}{2} \\ y=325 \end{gathered}\)Therefore, the cost of the bench is 325.
Briana has 4 1/2 cups of oats. She uses 2 1/4 cups of oats to make oatmeal- raisins cookies, then borrow 1 cup of oats from her neighbor. Her recipe for granola calls 2 1/2 cups of oats. Does she have enough? How much will she have left over, or how much more will she need?
Answers
Answer:
She has enough with \(\frac{3}{4}\) cups left over.
Step-by-step explanation:
For this equation, it's probably easiest to use improper fractions.
At the start, she has 4\(\frac{1}{2}\) cups, or \(\frac{9}{2}\), which can be converted to \(\frac{18}{4}\) (which is useful for the next part) by multiplying the numerator and denominator by 2.
When she uses 2\(\frac{1}{4}\) cups, which can be converted to \(\frac{9}{4}\). When subtracting this from the original, you get \(\frac{18}{4}\)-\(\frac{9}{4}\)=\(\frac{9}{4}\).
She borrows another cup, or \(\frac{4}{4}\) of a cup, which gets added on to the previous result, giving \(\frac{9}{4}\)+ \(\frac{4}{4}\)=\(\frac{13}{4}\).
The recipe calls for 2\(\frac{1}{2}\) cups, which can be converted to \(\frac{5}{2}\) or \(\frac{10}{4}\).
\(\frac{13}{4}\)-\(\frac{10}{4}\)=\(\frac{3}{4}\), meaning she has \(\frac{3}{4}\) cups left over.
** solving this mainly uses conversion to improper fractions and adding/subtracting fractions, which may be skills you would like to practice. I'm always happy to help!
There are a total of 64 students in a drama club and a yearbook club. The drama club has 10 more students than the yearbook club.
a. Write a system of linear equations that represents this situation. Let x represent the number of students in the drama club and y represent the number of students in the yearbook club.
System of equations: x=
x+
y=64
Question 2
b. How many students are in the drama club? the yearbook club?
Answers
Answer:
x = y +10; x +y = 64x = 37; y = 2737 in drama club; 27 in yearbook clubStep-by-step explanation:
The equations will reflect the relations given in the problem statement:
x = y +10 . . . . . . 10 more in drama club than yearbook club
x + y = 64 . . . . . total of 64 students in both clubs
__
If we use the first equation to substitute for x in the second equation, we get ...
(y +10) +y = 64
2y = 54 . . . . . . . subtract 10
y = 27 . . . . . . . divide by 2
x = y +10 = 27 +10 = 37
There are 37 students in the drama club; 27 in the yearbook club.
what percentage of the total sum of squares can be accounted for by the estimated regression equation (to decimal)?
Answers
The percentage of the total sum of the squares that can be accounted for by the estimation of regression is 51.3% when it is taken in three decimal points by the regression equation.
The regression equation is used to find one variable from another known variable. There are two types to find the regression equation they are:
1. Regression equation by using simultaneous equation 2. Regression line
The regression equation can be found by the be calculated by the sums of squares by the the sample of correlation coefficient that is 0.716. The amount of variation is taken by the total variation that is interpreted and is denoted by 'r', the sum of squares can be calculated by 1-SSE/ SST=(SST/SST = SSR/SST. When it comes to the product volume then the percentage is 93.64% where it also includes the product cost and variable cost of the product.
To know more about percentage:
https://brainly.com/question/28206078
#SPJ4
DON'T tell me it's easy or whatever because I'm having a hard time understanding it and someone on my last question WASTED my points.
PLEASE HELP ASAP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
(02.07 LC)
Two similar triangles are shown below:
Which two sets of angles are corresponding angles?
∠e and ∠h; ∠f and ∠g
∠e and ∠i; ∠f and ∠h
∠e and ∠g; ∠f and ∠h
∠e and ∠i; ∠f and ∠g

Answers
Answer:
im pretty sure the answer is ∠e and ∠i; ∠f and ∠g
but if not im so sorry :(
Answer:
The third answer
Step-by-step explanation:
Each angle on both triangles has a set of lines, either one, two, or three. These lines are used to show congruency over a number of lines or angles. So one angle will correlate with whatever other angles have that same number of lines. For example, e and g both have two lines, this means they are corresponding and congruent.
Kuta Software - Infinite Algebra 1 Name___________________________________ Adding and Subtracting Polynomials
Answers
Kuta Software - Infinite Algebra 1 is an educational tool that focuses on providing students with algebra 1 exercises. The software includes a range of topics that cover the fundamentals of algebra 1. One of the topics that the software covers is Adding and Subtracting Polynomials. Adding Polynomials involves combining like terms.
In the case where the polynomials are in descending order, students can start adding or subtracting their respective terms. Similarly, if the polynomials are in ascending order, the students should start with the terms with the highest degree and work their way down. Adding polynomials is relatively easy since it involves combining like terms.
However, when it comes to subtracting polynomials, the process becomes a bit more complicated. The subtraction of polynomials involves changing the sign of the terms to be subtracted. To be able to do this, students can first distribute a negative sign throughout the polynomial, then follow the same procedure they would have followed when adding polynomials to combine like terms.
To know more about Polynomials visit:
https://brainly.com/question/11536910
#SPJ11
Adding and subtracting polynomials in Algebra involves combining or subtracting like terms. For practice, Kuta Software provides various activities. An example is given to demonstrate the process.
Explanation:Adding and subtracting polynomials is a key concept within the subject of Algebra 1. Kuta Software is a common educational platform that offers a variety of activities for practicing this skill. In essence, to add or subtract polynomials, you combine or subtract like terms, which are terms with the same variable and exponent. For example, if you were to add the polynomials 3x^2 + 2x and 5x^2 - 2x, you would combine the x^2 terms and the x terms separately, resulting in (3x^2 + 5x^2) + (2x - 2x), which simplifies to 8x^2.
Learn more about Adding and Subtracting Polynomials here:https://brainly.com/question/35934946
Marcus has a box that is 4 feet long, , foot wide, and 2 feet high. What is the volume of the box? PLS HURRY I WILL DO ANYTHING
Answers
Answer:
8 feet cubed
Step-by-step explanation:
4 x 2 x 1
Write an equation for the nth term of the geometric sequence. Then find a7.
1,-2,4,-8...
Answers
Answer:
1,2,4,6,-8....
Step-by-step explanation:
Map Proportionality: You have a map where Indy and Fort Wayne are 19 centimeter apart. Kokomo and Indy are 9.5 cm apart on the map. If you know that Indy and Fort Wayne are actually 120 miles apart, how far apart would Indy and Kokomo be in real life? Express your answer rounded to the nearest tenth of
Answers
Answer: 60 miles
Step-by-step explanation:
On a map, Indy and Fort Wayne are 19 centimeter apart while Kokomo and Indy are 9.5 cm apart on the map.
In real life, Indy and Fort Wayne are actually 120 miles apart, the distance between Indy and Kokomo in real life would then be:
= 9.5 × 120/19
= 120/2
= 60 miles
Indy and Kokomo are 60 miles apart in real life.
Find the MAD for this set of data.
Swim Team
Name Age (years) Mean
Maddox
Enrique
13
Gloria
9
McKenna 10
Asher
10
Hannah
9
Danielle
Katy
Timothy
Gentry
10
10
11
9
9
10
10
10
10
10
10
10
10
10
10
Absolute
Deviation
1
3
1
0
0
1
0
0
1
1
MAD =
?
DONE
Answers
The mean absolute deviation (MAD) of the given data set is 0.8.
How to calculate the mean absolute deviation of a data set?Mean absolute deviation (MAD) is a measure of the average absolute distance between each data value and the mean of a data set. The formula for MAD is:
MAD = ∑|x-m|/n
∑ is known as Sigma and means to sum up
| | are vertical bars that mean absolute value
x is each value
m is the mean
n is the total number of data points in your data set
∑|x-m| is sum of Absolute Deviation
Using the table, the sum of Absolute Deviation will be:
∑|x-m| = 1 + 3 + 1 + 0 + 0 + 1 + 0 + 0 + 1 + 1 = 8
n = 10
MAD = ∑|x-m|/n = 8/10 = 0.8
Therefore, the mean absolute deviation of the set data is 0.8
Learn more about mean absolute deviation on:
brainly.com/question/16586775
#SPJ1
Complete Question
Check the attached image for table of data

Factor completely: 64x^3+1
Answers
Answer:
Step-by-step explanation:
Sum of cubes is a^3+b^3=(a+b)(a^2-ab+b^2)
64x^3+1
(4x+1)(16x^2-4x+1)
Simplify.
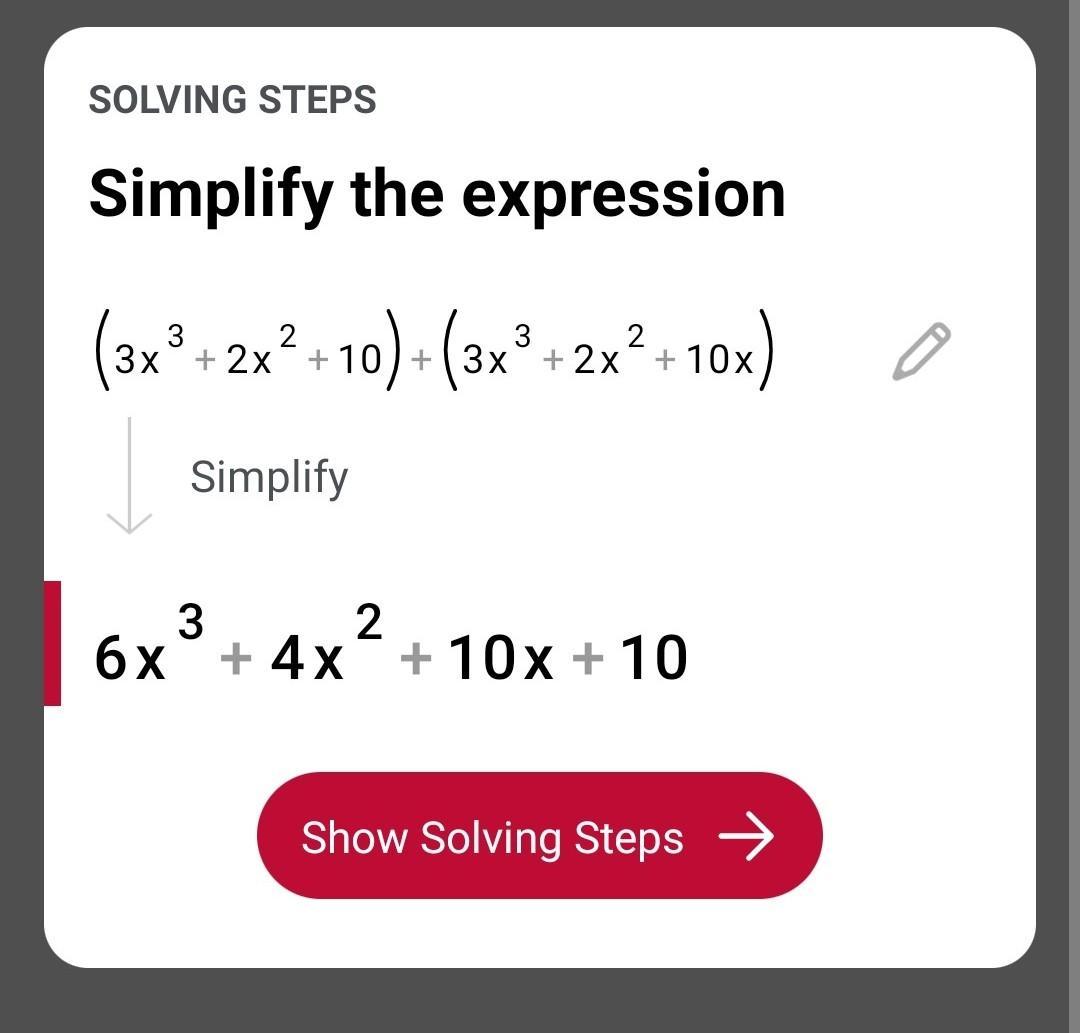
(3x^3 + 2x^2 + 10) + (3x^3 + 2x^2 + 10x)
A) 3x^3 + 2x^2 + 10x + 10
B) 6x^3 + 4x^2 + 20x
C) 6x^3 + 4x^2 + 10x + 10
D) 9x^3 + 4x^2 + 100x
Answers
Answer:
look at it.. ogogogogogogogogogoogogogog
A particle moves along the y-axis so that at time t≥0 its position is given by y(t)=t3−6t2+9t. Over the time interval 0
Answers
Therefore, the maximum displacement of the particle is 4 units, and it occurs at time t = 1.
To find the maximum displacement, we need to first determine the particle's velocity and acceleration.
The velocity of the particle is given by the derivative of its position function:
\(v(t) = y'(t) = 3t^2 - 12t + 9\)
The acceleration of the particle is given by the derivative of its velocity function: a(t) = v'(t) = 6t - 12
Now, to find the maximum displacement, we need to find the time at which the particle comes to rest.
This occurs when its velocity is zero:
\(3t^2 - 12t + 9 = 0\)
Simplifying this equation, we get:
\(t^2 - 4t + 3 = 0\)
This quadratic equation factors as:
(t - 1)(t - 3) = 0
So the particle comes to rest at t = 1 or t = 3.
Next, we need to determine whether the particle is at a maximum or minimum at each of these times.
To do this, we look at the sign of the acceleration:
When t = 1, a(1) = 6(1) - 12 = -6, which is negative.
Therefore, the particle is at a maximum at t = 1.
When t = 3, a(3) = 6(3) - 12 = 6, which is positive.
Therefore, the particle is at a minimum at t = 3.
Finally, we need to find the displacement of the particle at each of these times:
\(y(1) = 1^3 - 6(1)^2 + 9(1) = 4\)
\(y(3) = 3^3 - 6(3)^2 + 9(3) = 0.\)
For similar question on displacement.
https://brainly.com/question/1581502
#SPJ11
y-30≥32 lol i need help again
Answers
Answer:
y ≥ 62
Step-by-step explanation:
Give Me Brainllest plz T - T

three times a number, added to 4, is 40
Answers
Answer:
12
Step-by-step explanation:
12 × 3= 36
36 + 4= 40
so the answer is 12
Answer:
Not true with all numbers!
Step-by-step explanation:
see.Ex.3x3=9+4=13 not 40
Please help me, thank you :)

Answers
Answer:
14+14 + 4pi= 28 + 4pi
\(\pi\)
Area of rectangle = 14*4= 56
Area of circle = 4pi
Add them together. 56 + 4pi = 68.6
find the p-value (to two significant digits) for the following test. h0: μ ≤ 0, h1: μ > 0, σ = 1, z = 1.5 hint: the population follows the standard normal distribution.
Answers
The p-value for the given test is approximately 0.067, rounded to two significant digits. This was calculated by finding the area to the right of z=1.5 under the standard normal distribution.
It is given that Null hypothesis: H0: μ ≤ 0, Alternative hypothesis: H1: μ > 0, Population standard deviation: σ = 1, Test statistic: z = 1.5
To find the p-value, we need to calculate the probability of observing a z-value of 1.5 or greater under the null hypothesis. Since the population follows the standard normal distribution, we can use a standard normal table or a calculator to find this probability.
Using calculator, we can find that the area to the right of z = 1.5 is approximately 0.0668 (rounded to four decimal places).
Since this is a one-tailed test with the alternative hypothesis in the right tail, the p-value is equal to the area in the right tail beyond the observed z-value. Therefore, the p-value for the test is approximately 0.067 (rounded to two significant digits).
So, the p-value for the given test is 0.067 (rounded to two significant digits).
To know more about p-value:
https://brainly.com/question/30461126
#SPJ4
Taylor is proving the Pythagorean theorem.
(photo attached)
How could Taylor use the diagram to prove the Pythagorean theorem?
A. Taylor could set the area of a square with side length a + b equal to the sum of the areas of the 4 triangles and the square with side length c.
B. Taylor could set the area of the square with side length c equal to the sum of the areas of the 4 congruent triangles.
C. Taylor could find the ratio of the area of the square with side length a + b to the area of one of the congruent triangles.
D. Taylor could find the ratio of the area of the square with side length a + b to the area of the square with side length c.

Answers
If Taylor is proving the Pythagorean theorem. Taylor can use the diagram to prove the Pythagorean theorem by: A. Taylor could set the area of a square with side length a + b equal to the sum of the areas of the 4 triangles and the square with side length c.
How could Taylor use the diagram to prove the Pythagorean theorem?To prove the Pythagorean theorem, we want to show that in a right triangle with legs a and b and hypotenuse c, the square of the hypotenuse c^2 is equal to the sum of the squares of the legs a^2 + b^2.
From the given diagram, we can see that we have a square with side length a+b, which is divided into 4 congruent right triangles and a smaller square with side length c. Each of the 4 triangles has legs a and b, which are also the legs of the right triangle we want to prove the theorem for. The smaller square with side length c has an area equal to c^2, which is the square of the hypotenuse of the right triangle.
The area of the square with side length a+b is (a+b)^2 = a^2 + 2ab + b^2. The area of one of the congruent right triangles is (1/2)ab, so the sum of the areas of the 4 triangles is 2ab. Therefore, the sum of the areas of the 4 triangles and the smaller square is:
a^2 + 2ab + b^2 + c^2
But this is also equal to the area of the larger square with side length a+b, which is (a+b)^2. So we have:
a^2 + 2ab + b^2 + c^2 = (a+b)^2
Expanding the right-hand side gives:
a^2 + 2ab + b^2 + c^2 = a^2 + 2ab + b^2
Canceling the common terms on both sides gives:
c^2 = a^2 + b^2
This is the Pythagorean theorem, which we have proved using the given diagram.
Therefore, option A is the correct answer.
Learn more about Pythagorean theorem here:https://brainly.com/question/343682
#SPJ1
If Joan is buying a purse that is regularly priced at $407.99 and there is a sale sticker on it that says 27% off, which expression could not be used to find out the new price of the purse?
A.
407.99 • 0.73
B.
407.99 ‒ (407.99 • 0.27)
C.
407.99 × 73%
D.
407.99 • 0.27
Answers
The expression that could not be used to find out the new price of the purse is 407.99 • 0.27 .
in the question ,
it is given that
the regular price of the purse is $407.99
discount percent on the purse = 27% .
Since 27% is discount , so the new price will be
new price = original price ( 100- discount percent)
= 407.99*(100-27%)
= 407.99*73%
which is option (C)
on simplifying 407.99*73% , we get
= 407.99*0.73 ........ 73% = 0.73
which is option(A)
also the new price can be given by
new price = regular price - (regular price) * ( discount percent)
So ,
new price = 407.99 ‒ (407.99 • 0.27)
which is option (B)
only option(D) is missing
Therefore , The expression that could not be used to find out the new price of the purse is 407.99 • 0.27 , the correct option is (D) .
Learn more about Discount here
https://brainly.com/question/19260665
#SPJ1