DO U LIKE MATHEMATICS QUESTIONS
Answers
Answer:
No lol
Step-by-step explanation:
I actually hate maths..
Related Questions
Name a pair of lines that are perpendicular
Answers
Answer:
Two distinct lines intersecting each other at 90° or a right angle are called perpendicular lines. Here, AB is perpendicular to XY because AB and XY intersect each other at 90°. The two lines are parallel and do not intersect each other. They can never be perpendicular to each other.
Step-by-step explanation:
hope it helps:)
Have a screenshot of math question, check pick below plz thanks

Answers
Answer:
i dont see it
Step-by-step explanation:
Together, Steve and Tom sold 125 raffle tickets for their school. Steve sold 17 more than three times as many raffle tickets as Tom. How many raffle tickets did each boy sell?
Answers
Tom sold 27 raffle tickets and Steve sold 98 raffle tickets.
What is an equation?Two algebraic expressions having the same value and symbol '=' in between are called an equation.
Given:
Together, Steve and Tom sold 125 raffle tickets for their school.
Steve sold 17 more than three times as many raffle tickets as Tom.
Let s be the number of raffle tickets sold by Steve and t be the raffle tickets sold by Tom.
So,
3t + 17 + t = 125
4t = 108
t = 27
And s = 98
Therefore, Steve sold 98 and Tom sold 27 tickets.
To learn more about the equation;
https://brainly.com/question/12788590
#SPJ1
If 15% of the customers total is $98,880, then the sum total equals what
Answers
The sum total by the given data is equals to $658,880.
We are given that;
Percent=15%
Amount= $98,880
Suppose the value of which a thing is expressed in percentage is "a'
Suppose the percent that considered thing is of "a" is b%
Then since percent shows per 100 (since cent means 100), thus we will first divide the whole part in 100 parts and then we multiply it with b so that we collect b items per 100 items(that is exactly what b per cent means).
To divide by a percentage, we can convert it to a decimal by moving the decimal point two places to the left. This gives us:
15% = 0.15
To divide by 0.15, we can multiply by its reciprocal, which is 1/0.15. This gives us:
$98,880 / 0.15 = $98,880 x 1/0.15
To multiply by 100, we can move the decimal point two places to the right. This gives us:
$98,880 x 1/0.15 x 100 = $658,880
Therefore, by the percentage the answer will be $658,880.
Learn more about percent here:
https://brainly.com/question/11549320
#SPJ1
1+2*3-4. Please answer
Answers
Answer:1(2x3)-4= 3
2x3= 6 -4=2+1=3
Step-by-step explanation:
Answer:
3
Step-by-step explanation:
2x3=6
1+6=7
7-4=3
What is the answers to Part A, B, and C ?

Answers
Part a: The data points appear to follow an exponential pattern. This is because the balance is increasing at a rate that is proportional to the current balance.
How to explain the informationPart b: The equation of the best fit is y = 50(1.06)^x. This can be found using a variety of methods, including graphing the data points and fitting a curve to them, or using a statistical software package.
Part c: When x = 32, y = 50(1.06)^32 = $2,499.82.
Years since 1990, x 0 5 10 15 20 25 30
Balance, y $50 $62.31 $77.65 $96.76 $120.59 $150.27 $187.27 $2,499.82
The equation of the fitted curve is y = 50(1.06)^x.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
find the following arc measures

Answers
The measure of the angles are;
<KL = 23 degrees
m<LON is 23 degrees
m<OM = 113 degrees
m<KNL = 23 degrees
m<NL = 157 degrees
How to determine the measures of the arcTo determine the measures of the arc, we need to note the following;
Angles on a straight line is equal to 180 degreesAngle at right angle is equal to 90 degreesFrom the information shown in the diagram, we have;
<KL +<KM = 90 degrees
Now, substitute the values
<KL + 67 = 90
collect like terms
<KL = 23 degrees
m<LON and <KL are corresponding angles
Then, m<LON is 23 degrees
m<OM = m<LON + 90 degrees
Substitute the values
m<OM = 113 degrees
m<KNL = 23 degrees
m<NL = 90 + <LM
Substitute the values
m<NL = 157 degrees
Learn more about angles at: https://brainly.com/question/25770607
#SPJ1
If x is semi-prime, how many prime factors does it have?
please, 20 points for this!!
Answers
Answer:
2 prime factors
Answer: 2 prime factors
Step-by-step explanation: A semiprime is a number n that has just 2 prime factors p and q so n = p × q. It is therefore "almost" a prime (which has only one prime factor, itself!) or a semiprime.
Find the slope of the line (4, 12) (10, 6)
Answers
help please !! i need help

Answers
Answer: 1/2x
Step-by-step explanation:
Hope it’s right
Pls help me. How long is GH?

Answers
mathmatically indication example with solution
Answers
A mathematically indication example would be to solve the equation 3x + 2 = 14 for the value of x. The solution would be 4.
How to solve the equation ?Looking for a mathematically indication example, we can consider a simple mathematical equation with one variable and solve it.
The equation would be 3 x + 2 = 14.
So we can solve for the equation to be :
3x + 2 - 2 = 14 - 2
3x = 12
3 x / 3 = 12 / 3
x = 4
In conclusion, the mathematically indication example would be 3x + 2 = 14 and the value of x would be 4.
Find out more on equation solutions at https://brainly.com/question/2228446
#SPJ1
PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)
Which statement is true. A. The square root of 150 is 15.
B. The square root of 400 is 40.
C. The square root of 36 is 18.
D. The square root of 256 is 16
Answers
Answer:
D. The square root of 256 is 16
Step-by-step explanation:
16^2 = 256
consider a two-factor factorial design with three levels for facts a, three levels for factor b, and four replicates in each of the nine cells
a. how many degrees of freedom are there in determining the A variation and the factor B variation
b. how many degrees of freedom are there in dreaming the interaction variation
c. how many degrees of freedom are there in determining the random variation
d. how many degrees of freedom are there in determining the total variation
Answers
In calculating the factor A variation, there are two degrees of freedom. In determining the variation of factor B, there are two degrees of freedom.
What is a two-factorial design?A two-factor factorial design is an experiment that collects data for all potential values of the two factors of the study. The design is a balanced two-factor factorial design if equivalent sample sizes are used for every of the possible factor combinations.
Suppose we have two components, A and B, each of which has a high number of levels of interest. We will select a random level of component A and a random level of factor B, and n observations will be taken for each experimental combination.
From the data given:
a.
In calculating the factor A variation, there are two degrees of freedom.
In determining the variation of factor B, there are two degrees of freedom.
b.
Finding the degree of freedom using the interaction variation, there are four degrees of freedom.
c.
In finding the random variable, there are 9(4-1) = 27 degrees of freedom.
d.
In calculating the total variable, there are 9*4-1 =35 degrees of freedom.
Learn more about using a two-factor factorial design for determining the degree of freedom here:
https://brainly.com/question/14292694
#SPJ1
4. Calculate the Social Security and Medicare tax that would be applied to an annual salary of $56,400.
Answers
Answer:759
Step-by-step explanation:
Anderson uses the discriminant to correctly find the number of real solutions of the quadratic equation one-halfx2 + 4x + 8 = 0. Which explanation could Anderson provide?
The equation has no real number solutions because the discriminant is 0.
The equation has one real number solution because the discriminant is 0.
The equation has no real number solutions because the discriminant is less than 0.
The equation has two real number solutions because the discriminant is greater than 0.
Answers
Answer:
The equation has one real number solution because the discriminant is 0.
Step-by-step explanation:
If the discriminant is less than 0, there are no real number solutions.If the discriminant is equal to 0, there is one real number solution.If the discriminant is greater than 0, there are two real number solutions.Formula: D = \(b^{2}\) - 4ac
\(\frac{1}{2} x^{2}+4x+8=0\)
⇒ a = 1/2, b = 4, c = 8
⇒ D = 4*4 - 4*0.5*8 = 16 - 16 = 0
⇒ The equation has one real number solution because the discriminant is 0.
Answer: B
Step-by-step explanation:
Kelly's little brother is exactly 3 feet tall. How tall is he in inches?
Answers
Answer:
he is 36 inches
Step-by-step explanation:
Answer:
36 inches
Step-by-step explanation:
We know that Kelly's little brother is exactly 3 feet tall, and we know how big he is in inches.
To solve first keep in mind that 1 feet is 12 inches.
Therefore if there are 3 feet, we would multiply the inches 3 times.
12 * 3
= 36
Therefore, Kelly's little brother is 36 inches.
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
* HELP QUICK I WILL MARK BRANLIEST* If the circumference of a circle is 10x inches, what is the area, in square inches, of
the circle?
1) 10 sq. in
2) 254 sq. in.
3) 50. sq. in.
4) 100 sq. in.

Answers
Answer:
100 Sq in.
Step-by-step explanation:
BIG IDEAS MATH
K
Tell whether the information in the figure allows you to conclude that point P lies on the perpendicular bisector of
LM.
L
P
M
Yes
O No
N
Explain your reasoning.
Answers
Note that it is correct to state that LN ≅ MN and Nk ⊥ LM, so NK is the perpendicular bisector of LM and P is on NK. See attached image.
What is a perpendicular bisector?A perpendicular bisector is a line that cuts another line segment across the junction point at a straight angle. As a result, a perpendicular bisector always cuts a line segment through its midway. The phrase bisect implies dividing evenly or uniformly.
A simple technique to determine a perpendicular bisector is to measure the line segment you need to bisect. Then, divide the measured length by two to determine the midway. Draw a line at a 90-degree angle out from this middle.
Learn more about perpendicular bisectors:
https://brainly.com/question/24753075
#SPJ1
Full Question:
Tell whether the information in the diagram allows you to conclude that point P lies on the perpendicular bisector of LM. Explain your reasoning. See attached image.
A) No. You would need to know that LK ⊥ MK
B) No. You would need to know that KP ⊥ LM
C) Yes, t LN ≅ MN and Nk ⊥ LM, so NK is the perpendicular bisector of LM and P is on NK
D) Yes, NK ⊥ LM, so NK is the perpendicular bisector of LM and P is on NK

A bowl contains a mixture of r red and b brown candies. Find values of r and b so that there is exactly a 50 percent chance that the colors of two randomly chosen candies will not match. There are many possibilities, including r = 15 and b = 10. Verify that these values work, then find other values for r and b (besides r = 10 and b = 15) that are consistent with this information. You could try small values for r
and b.
Answers
There are two possible sets of values for r and b that satisfy the condition: r = 1 and b = 2, and r = 4 and b = 3.
Now to find the values of r and b such that there is exactly a 50% chance that two randomly chosen candies will not match, we need to set up the following equation:
(r/b) x ((b-1)/(r+b-1)) + ((b/r) x (r-1)/(r+b-1)) = 1/2
Simplifying this equation, we get:
\(2r^2 - 2rb + 2b^2 - 3r + 3b = 0\)
We can solve for r in terms of b using the quadratic formula:
\(r = (2b ± √(4b^2 - 4(2b^2 - 3b))) / 4\)
Simplifying this expression, we get:
\(r = (b ± \sqrt{(5b^2 - 12b))} / 2\)
Since r and b must be positive integers, we can try small values of b and see if we get integer values for r. For example, if we let b = 2, then:
\(r = (2 ±\sqrt{ (5(2)^2 - 12(2))) } / 2\)
r = (2 ± √4) / 2
r = 1 or 3
So, if there are 2 brown candies and 1 or 3 red candies, there is a 50% chance that two randomly chosen candies will not match.
Similarly, if we let b = 3, then:
\(r = (3 ± \sqrt{(5(3)^2 - 12(3)))} / 2\)
r = (3 ± √21) / 2
Since the square root of 21 is irrational, we cannot get integer values for r in this case. However, we can use a decimal approximation for √21 to get approximate values for r. For example, if we use √21 ≈ 4.58, then:
r ≈ (3 ± 4.58) / 2
r ≈ 3.79 or 0.21
Since r must be a positive integer, the only possible solution is r = 4 and b = 3.
Thus, we have found two possible sets of values for r and b that satisfy the condition: r = 1 and b = 2, and r = 4 and b = 3.
To know more about probability visit:
https://brainly.com/question/30034780
#SPJ1
A circle has a radius of 4 ft.
What is the area of the sector formed by a central angle measuring 270 degrees
Use 3.14 for pi and round the decimal to the nearest tenth.
42.8 ft
37.7 ft
12 ft
9.4 ft
Answers
The area of the sector is 37.7 ft.
What is sector:
A sector is a region of a circle that is bounded by two radii and the arc of the circle that lies between the endpoints of those radii.
The formula for the area of a sector is given by
A = (θ/360)πr²Where θ is the central angle in degrees, and r is the radius of the circle
Here we have
A circle has a radius of 4 ft.
The central angle of sector formed = 270°
Using the formula, Area of sector = (θ/360°) × π r²
Area of the given sector = [ 270/360] × 3.14 × (4)²
= [0.75 ] × [50.24]
= 37.68 ft
= 37.7 ft
Therefore,
The area of the sector is 37.7 ft.
Learn more about Area of sector at
https://brainly.com/question/2998942
#SPJ1
Help me solve this please right answer I’ll give brainlist to.

Answers
Answer:
$237.44
Step-by-step explanation:
Find the solutions of the quadratic equation –9x2 + 49 = 0.
Answers
Answer:
x = 7/3
Step-by-step explanation:
Given equation:
–9x² + 49 = 0To determine the value of "x", we need to isolate the x-variable and it's coefficient on one side of the equation. This can be done by subtracting 49 to both sides of the equation.
⇒ –9x² + 49 - 49 = 0 - 49⇒ –9x² = -49We can see that the negative sign in on both sides of the equation. Remove it by dividing -1 to both sides of the equation.
⇒ –9x² = -49⇒ -9x²/-1 = -49/-1⇒ 9x² = 49Clearly, we can see that 9x² and 49 are perfect squares. Therefore,
⇒ 9x² = 49⇒ (3x)² = (7)²Take square root both sides of the equation:
⇒ √(3x)² = √(7)²⇒ 3x = 7To determine the value of "x", we need to isolate it "completely". This can be done by dividing 3 to both sides of the equation
⇒ 3x/3 = 7/3⇒ x = 7/3Therefore, the value of "x" must be 7/3.
Answer:
x = 7∕3, –7∕3
Step-by-step explanation:
To find the solutions of the quadratic equation -9x^2 + 49 = 0, we can solve for x by isolating x^2 first:
-9x^2 + 49 = 0
-9x^2 = -49
Dividing both sides by -9, we get:
x^2 = 49/9
Taking the square root of both sides, we get:
x = ± 7/3
Therefore, the solutions of the quadratic equation -9x^2 + 49 = 0 are x = 7/3 and x = -7/3.
A bank manager wants to encourage new customers to open accounts with principals of at least $3500. He decides to make a poster advertising a simple interest rate of 3%. What must the principal be if the bank manager also wants to advertise that one can earn $10 the first month?
Answers
The principal if the bank manager also wants to advertise that one can earn $10 the first month is $4000.
How to calculate the principal?From the information, the simple interest is $10 and the rate is illustrated as 3%.
The formula for the simple interest in a month is illustrated as:
S = (p × r × t/12 / 100)
r = rate
t = time
S = interest
Place the values in the formula:
10 = p × 3 × 1 / 100 × 12
10 = 3p/1200
Cross multiply
3p = 12000
Divide
p = 12000/3
p = 4000
The principal is $4000.
Learn more about principal on;
brainly.com/question/19105603
#SPJ1
Is 500% of less than 10, greater than 10 but less than 100, or greater than 100?
Answers
Answer: less
Step-by-step explanation:
If 100% of 10 is 10, we multiply 10 by 5 to get 500%.
10 x 5 = 50
500% of 10 will be equal to the number 50.
The answer is less.
Consider this function.
please help!
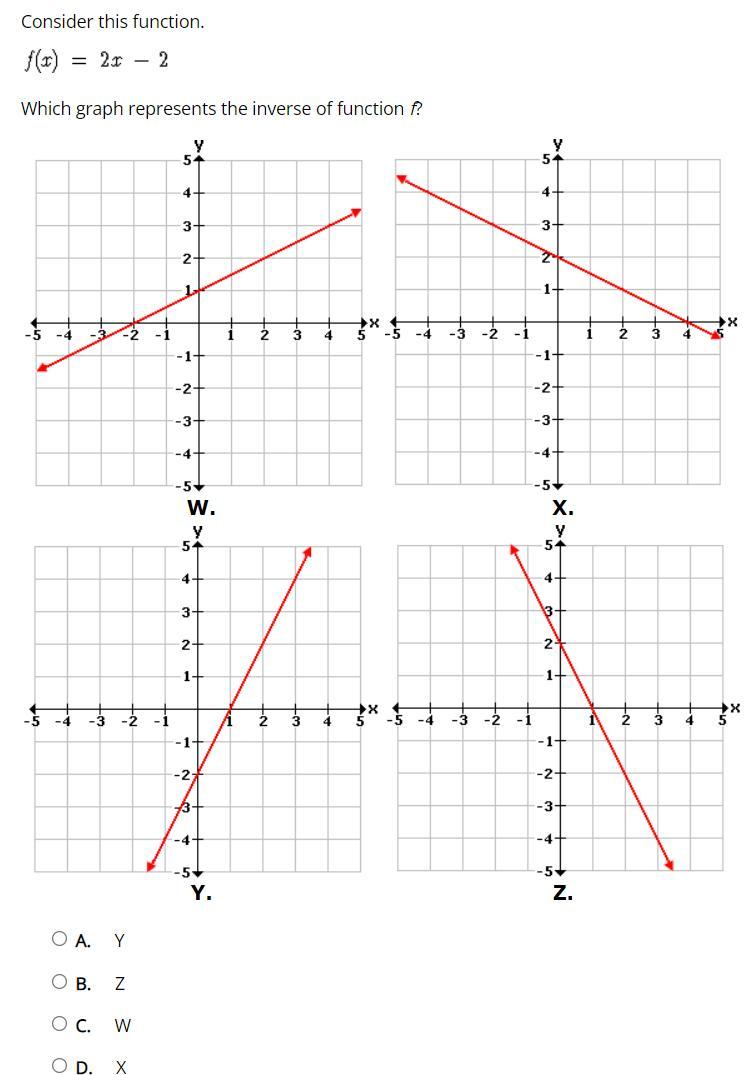
Answers
feel free to ask me if you didn't understand a part
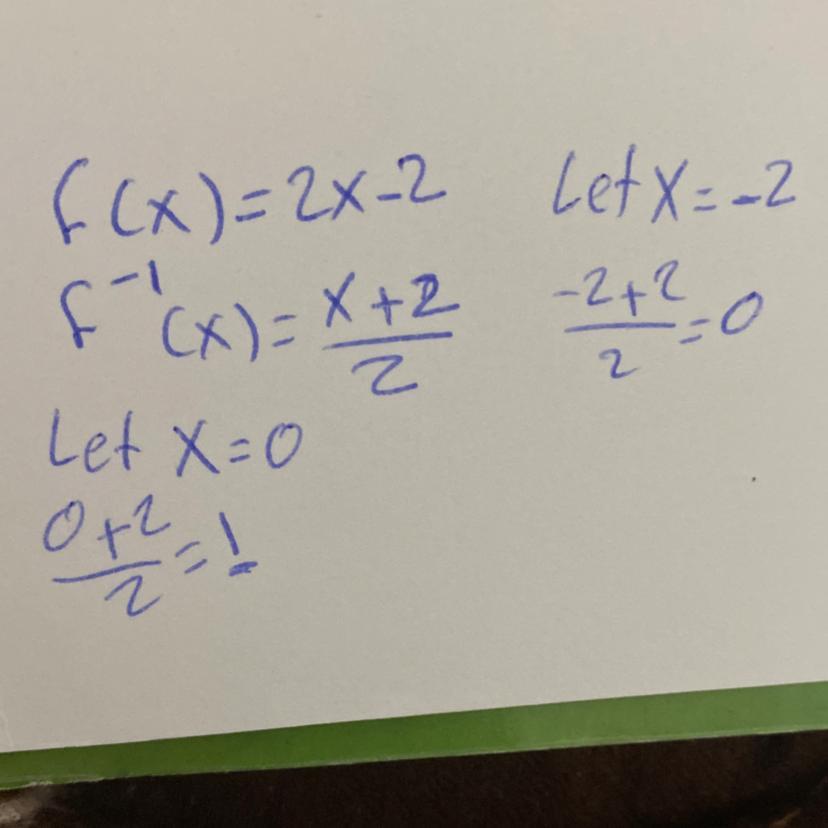
how many times can 8 go into 87
Answers
Answer:
10 times
Step-by-step explanation:
If you are talking about division, then we would do 87/8=10
Answer:
It can go 10.875 times.
Step-by-step explanation:
87/8 = 10.875
≈ 11
Hope this helps; have a great day!
hi guys, i have a percentage question that I am not sure.
Here is the question: A phone costing £500 is in a sale. The sale price is £400 what percentage off is this?
Answers
Answer:
20 percent
Step-by-step explanation:
\(\frac{400}{500}\)\(=0.8\)
\(1-0.8=0.2\)
This means that 20 percent off of 500 is 400.
Answer:
The answer should be 20%
Step-by-step explanation:
Hope this helps