Dominick and Ryan both invest $6,500 into savings accounts that earn 6. 8% interest. If Dominicks account earns compound interest and Ryan's earns simple interest, how much more interest will Dominick have earned after 10 years?
Answers
Dominick has earned $6,465.55 - $4,420.00 = $2,045.55 more interest than Ryan after 10 years.
How to find the earned interest?To solve this problem, we can use the formulas for compound interest and simple interest.
Compound interest formula:
\(A = P(1 + r/n)^(^n^t^)\)
Where:
A = the amount after time t
P = the principal
r = the annual interest rate
n = the number of times the interest is compounded per year
t = time in years
Simple interest formula:
I = Prt
Where:
I = the interest earned
P = the principal
r = the annual interest rate
t = time in years
Using the compound interest formula for Dominick's account:
\(A = P(1 + r/n)^(^n^t^)\)
A = 6500(1 + 0.068/365)^(365*10)
A ≈ $12,965.55
Using the simple interest formula for Ryan's account:
I = Prt
I = 65000.06810
I = $4,420.00
Dominick's account has earned: $12,965.55 - $6,500 = $6,465.55 in interest.
Ryan's account has earned: $4,420.00 in interest.
Therefore, Dominick has earned $6,465.55 - $4,420.00 = $2,045.55 more interest than Ryan after 10 years.
Learn more about Earned interest
brainly.com/question/31112017
#SPJ11
Related Questions
If a+5=b, then what is the value of (b-a)^4
Answers
Answer:82
Step-by-step explanation:
90 + 90 × 10%
= 90 + 90 × 0.10
= 90 + 9
= 99
Write as a fraction in lowest terms:

Answers
Answer:
\(\frac{79}{100}\)
Step-by-step explanation:
Question:
Write as a fraction in lowest terms:
Answer:
a = 79
b = 99
pls help for brainlest
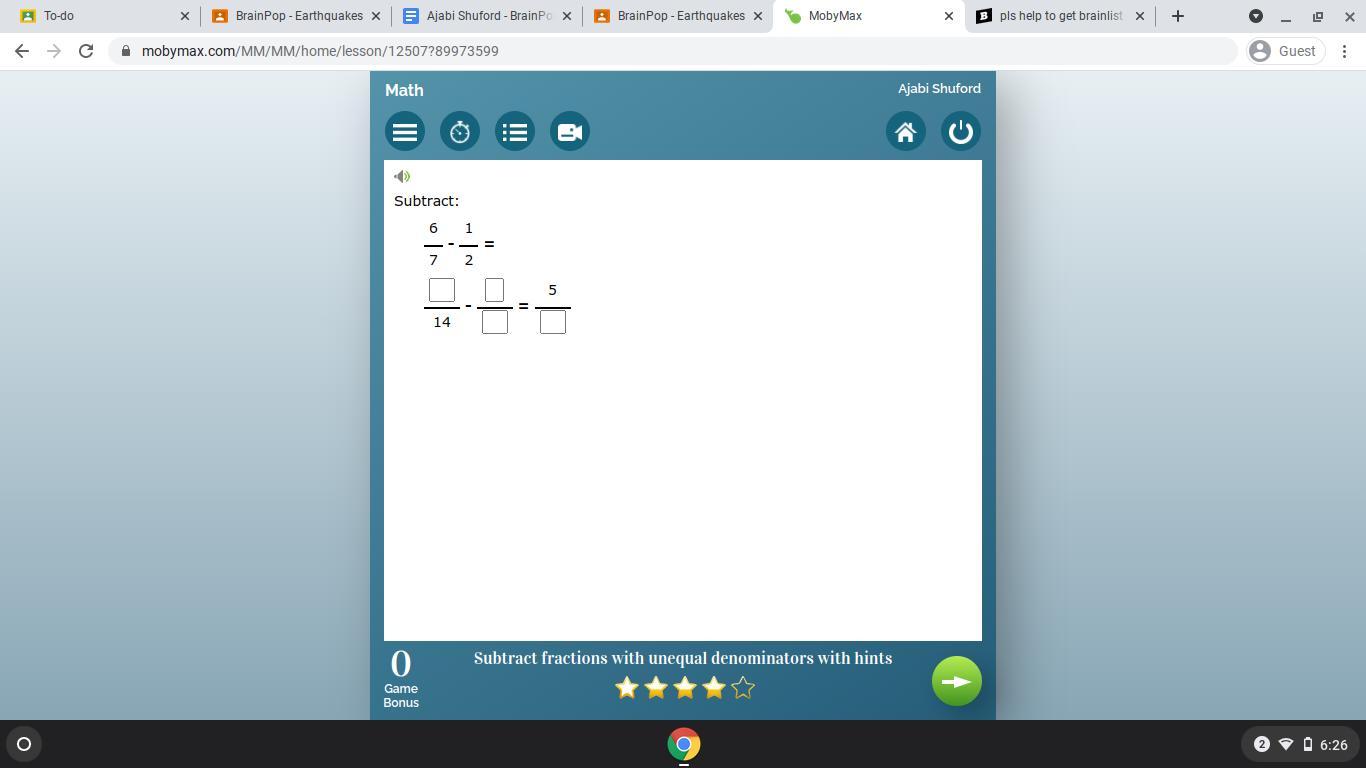
Answers
12/14+-7/14 . =5/14
lol
Use the drawing tool(s) to form the correct answer on the provided grid.
Lisa and Penny are guests at a beachside hotel. Lisa is laying on a towel at the beach which is 50 feet from the base of the hotel. When she looks up at an angle of 54.5 degrees, she can see her sister Penny waving to her from the hotel window.
Draw a scale representation of the triangle that models the situation and can be solved to find the straight-line distance between Penny and Lisa. Round calculations to the nearest foot. Each unit on the grid represents five feet.
Answers
Answer:
86 ft
Step-by-step explanation:
You want the straight line distance from a location 50 ft from a hotel to a window that has an angle of elevation of 54.5°.
CosineThe cosine relation between sides and angles in a right triangle is ...
Cos = Adjacent/Hypotenuse
The 50 ft distance is adjacent to the angle, and we want to find the hypotenuse. Using this equation, we can solve for the length we want:
Hypotenuse = Adjacent/Cos
ApplicationUsing the numbers in the problem statement, we find the straight-line distance to be ...
LW = LH/cos(54.5°) = (50 ft)/0.580703 ≈ 86 ft
The distance between Penny and Lisa is about 86 feet.
__
Additional comment
We don't know what drawing tools you have available. The attached diagram was drawn by locating the window at 50tan(54.5°) up from the base of the hotel. The tool provided the length of LW as 86.1.
We could have use a rotation tool to create the angle of 54.5°, or a line graphing tool to draw the line through (50, 0) with slope tan(-54.5°). Then an intersection tool could have located the window at the point of intersection of that line and the y-axis.
The calculation we did above is about the easiest for determining the distance mathematically (not having the tool measure it).
<95141404393>

For each geometric sequence given, write the next three terms a4, a5, and ag.
3, 6, 12,
a4 =____
a5= ____
a6= ____
Answers
The next three terms in the given geometric sequence are 24, 48, and 96
To find the next terms in the geometric sequence 3, 6, 12, we need to find the common ratio (r) first.
r = 6/3 = 2
Now we can use the formula for the nth term of a geometric sequence:
an = a1 * r^(n-1)
where n+1 is the nth term, a1 is the first term, r is the common ratio, and n is the term number.
Using this formula, we can find:
a4 = 24 (3 * 2^3)
a5 = 48 (3 * 2^4)
a6 = 96 (3 * 2^5)
Therefore, the next three terms in the sequence are 24, 48, and 96.
To learn more about geometric sequence go to:
https://brainly.com/question/13008517#
#SPJ11
A snail travels 48 inches per hour. Choose all the metric measures that are faster than 48 inches per hour
Answers
The value of 48 inches/hour is 121.92 centimetres/hour.
What is an expression?In mathematics, expression is defined as the relationship of numbers, variables, and functions using mathematical signs such as addition, subtraction, multiplication, and division.
To compare the speed of 48 inches per hour with metric measures, we need to convert inches to metric units. One way to do this is to use the conversion factor of 1 inch = 2.54 centimetres.
48 inches per hour is equivalent to:
48 inches/hour x 2.54 centimeters/inch = 121.92 centimeters/hour
To find all the metric measures that are faster than 48 inches per hour, we can convert 121.92 centimetres/hour to other units of measure. Here are some options:
1.2192 meters/hour: This is faster than 121.92 centimetres/hour because 1 meter = 100 centimetres.
0.0759 miles/hour: This is faster than 48 inches/hour because 1 mile = 63,360 inches.
Therefore, the metric measures that are faster than 48 inches per hour are 1.2192 meters/hour, 0.0759 miles/hour, and 0.042 knots.
To know more about an expression follow
https://brainly.com/question/3955273
#SPJ1
I NEED HELP FASTTTTTTT

Answers
Answer:
D
Step-by-step explanation:
i hope this helps!
Colton was given a box of assorted chocolates for his birthday. Each night, Colton treated himself to some chocolates. There were originally 30 chocolates in the box and Colton ate 2 chocolates each night. Write an equation for C,C, in terms of t,t, representing the number of chocolates remaining in the box tt days after Colton's birthday.
Answers
Answer:
C = -2t + 30
Step-by-step explanation:
y´all help a girl out- like bro what´re you supposed to do-


Answers
Answer:
1. y = 2/3x
2. P, y=-3x
Step-by-step explanation:
1. The constant k in the proportion y=kx can be found as ...
k = y/x . . . . for any x-y pair
The first pair gives ...
k = 2/3
So, the relation is ...
y = 2/3x
__
2. The y-intercept is 0, so the relation is proportional.
The constant of proportionality k can be found from the graph by finding the value of y when x=1. We know that a point on the graph is (-1, 3), and we can also see that the line goes through (1, -3)
y = -3x
If SSR (regression sum of squares) is 1200 and MSE (mean square error) is 20 from a simple regression which uses 22 data observations, then the R2 is _____.
Select one:
0.95
0.65
0.35
0.75
Answers
If SSR (regression sum of squares) is 1200 and MSE (mean square error) is 20 from a simple regression which uses 22 data observations, then the R² is 0.75.
In a simple linear regression, the total variation in the dependent variable (y) can be partitioned into two parts: explained variation due to the regression model and unexplained variation due to random error. The proportion of the total variation in y that is explained by the regression model is measured by the coefficient of determination, R².
R² is calculated as SSR/SST, where SSR is the regression sum of squares (variation explained by the regression model) and SST is the total sum of squares (variation in y around its mean).
Since we are given that SSR = 1200 and the regression model has one predictor variable, the degrees of freedom for SSR is 1. Therefore, SST = SSR + SSE (sum of squares error), where SSE = MSE*(n-2), with MSE being the mean square error and n being the sample size (number of observations).
Substituting the given values, we get: SST = 1200 + 20*(22-2) = 1600.
Thus, R² = SSR/SST = 1200/1600 = 0.75. Therefore, the answer is 0.75.
To know more about simple regression, refer here:
https://brainly.com/question/14313391#
#SPJ11
the diameter of a circle is 5.3 cm. What is the circumference
Answers
Answer:
16.642cm
Step-by-step explanation:
Diameter of a circle = 5.3cm
Circumference of a circle = π(d)
= π x 5.3
= 3.14 x 5.3
= 16.642cm
Answer:
C= pi x diameter
= 5.3pi
Answer is 16.65cm to 2 d.p
Hope this helps!
in the figure, a 60-cm length of uniform wire, of 60 g mass and negligible thickness, is bent into a right triangle. the x and y coordinates of the center of mass, in cm, are closest to
Answers
The center of mass of the right triangle is 2.14
The term center of mass refer a point where the whole mass of the body is supposed to be concentrated.
Here we have given that a 60-cm length of uniform wire, of 60 g mass and negligible thickness, is bent into a right triangle.
And we need to find the center of mass.
According to the following diagram, we have identified the values of
m1 = 24
m2 = 26
m3 = 20
r1 = 5
r2 = 5
r3 = 0
Then based on these values the center of mass is calculated as,
=> [(24 x 5) + (26 x 5) + (20 x 0)]/[24 + 26 + 20]
When we simplify this one then we get,
=> [ 120 + 130 + 0] / 70
Further simplification leads the value of,
=> 150/70
=>15/7
When we simplify this fraction into decimal then we get,
=> 2.14
To know more about center of mass here.
https://brainly.com/question/27549055
#SPJ4

Choose the letter of the correct answer
Why is the side AC congruent to itself?
A. Linear Pair
B. Reflexive Property
C. Vertical Angles are congruent
D. Alternate Interior Angles are Congruent
E. Given

Answers
In 30-60-90 triangle, the shorter leg is 6 ft long. Find the length to the nearest tenth of a foot of the other two sides.
Answers
Answer:
"In
In a 30-60-90 triangle, the sides are in a ratio of 1:√3:2.
So, the hypotenuse of the triangle is 62 = 12 ft long.
The longer leg of the triangle is 6√3 = 10.8 ft long (to the nearest tenth of a foot)
What is 200% of 190?
Answers
Review the proof of the identity cos(π − A) = −cosA.
cos(π − A)
Step 1: = cosπcosA − sinAsinπ
Step 2: = (−1)(cosA) + (sinA)(0)
Step 3: = −1cosA + (sinA)(0)
Step 4: = −cosA + 0
Step 5: = −cosA
At which step was an error made?
step 1
step 2
step 3
step 4
Answers
In the proof of given identity, cos(π - A) = -cos A. Therefore, step 1 is error made.
What are trigonometric identities?Trigonometric Identities are equality statements that hold true for all values of the variables in the equation and that use trigonometry functions. There are numerous distinctive trigonometric identities that relate a triangle's side length and angle.
The given identity is,
cos(π - A) = -cos A.
Use formula for cos(a − b) = cosa . cosb + sina . sinb
cos(π - A) = cosπcosA + sinAsinπ
= (−1)(cosA) + (sinA)(0)
= −1.cosA + (sinA)(0)
= −cosA + 0
= −cosA
Since, in the step 1 the formula is wrongly used,
Therefore, step 1 is error made.
To know more about Trigonometric identities on:
https://brainly.com/question/24377281
#SPJ1
How do you find the average value of a function?
Answers
The average value of function f(x) over [a,b] = 1/(b-a) × definite integral of f(x) over [a,b]
To find the average value of a function f(x) over an interval [a,b], you need to follow these steps:
Calculate the definite integral of the function f(x) over the interval [a,b]. The definite integral will give you the total area under the curve of the function over the interval.
Find the length of the interval [a,b] by subtracting the lower bound a from the upper bound b. The length of the interval will be (b-a).
Divide the value of the definite integral by the length of the interval to get the average value of the function over the interval [a,b]. That is:
Average value of f(x) over [a,b] = 1/(b-a) × definite integral of f(x) over [a,b]
So, the average value of a function over an interval is simply the total area under the curve of the function over that interval divided by the length of the interval.
Learn more about average value here
brainly.com/question/22847740
#SPJ4
Let X be a continuous random variable with probability density function defined by What value must k take for this to be a valid density?
Answers
The value of k that makes the given function a valid probability density function is k = 6.
To be a valid probability density function, the given function must satisfy the following two conditions:
The function must be non-negative for all possible values of X.
The integral of the function over all possible values of X must equal 1.
Using these conditions, we can determine the value of k as follows:
For the function to be non-negative, kx(1-x) must be non-negative for all possible values of X. This requires that k must be non-negative as well.
To find the value of k such that the integral of the function over all possible values of X is equal to 1, we integrate the given function from 0 to 1 and set the result equal to 1:
∫\(0^1 kx(1-x) dx = 1\)
Solving the integral gives:
k/6 = 1
k = 6
Learn more about probability
https://brainly.com/question/30034780
#SPJ4
X= 3y-5
2x + 12y = -4
This is a system of equations can somebody solve it you can use any method
Answers
Answer:
x = -4, y = 1/3
Step-by-step explanation:
=> x = 3y-5 (Equation 1)
=> 2x+12y = -4 (Equation 2)
Putting (1) in (2)
=> 2(3y-5)+12y = -4
=> 6y-10+12y = -4
=> 18y = -4+10
=> 18y = 6
Dividing both sides by 18
=> y = 6/18
=> y = 1/3
Putting y = 1/3 in Equation 1
=> x = 3(1/3)-5
=> x = 1-5
=> x = -4
2x+12y=-4
(-2)x=-6y+10
2x+12y=-4
12y=6
y=1/2
x=3y-5
2x+12y=-4
(-4)x=-12y+20
2x+12y=-4
-2x=16
x=-8
Construct the probability distribution by completing and the table below. Round tp three decimal places as needed. x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | p(x)| 7 | 14 | 32 | 56 | 43 | 27 | 15
Answers
The probability distribution can be constructed by dividing each value of p(x) by the sum of all p(x) values. This will give the proportion of each value in the distribution. The completed table is as follows: x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | p(x)| 0.030 | 0.061 | 0.139 | 0.243 | 0.186 | 0.117 | 0.064.
To construct the probability distribution, we need to find the probabilities for each value of x. The p(x) values given in the table represent the frequencies or counts of each value. To convert these counts into probabilities, we need to divide each p(x) value by the sum of all p(x) values.
In this case, the sum of all p(x) values is 7 + 14 + 32 + 56 + 43 + 27 + 15 = 194. To find the probability for each x value, divide each p(x) value by 194.
For example, the probability for x=0 is 7/194 ≈ 0.036. Similarly, the probability for x=1 is 14/194 ≈ 0.072, and so on.
The completed probability distribution table is as follows:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | p(x)| 0.036 | 0.072 | 0.165 | 0.289 | 0.222 | 0.140 | 0.082.
To know more about Frequencies visit.
https://brainly.com/question/33515650
#SPJ11
Pleaseee helppp answer correctly !!!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!!!!

Answers
Answer:
5 units
Step-by-step explanation:
Find the area of each regular polygon shown below. Round your answers to the nearest tenth, if necessary.

Answers
The area of the regular polygon is 280. 26 square inches
How to determine the areaWe can see from the diagram shown, that the polygon drawn is a hexagon, that is, a regular polygon with six sides.
The formula for calculating the area of a polygon is expressed as;
A = 3√3/2 a²
Given that the parameters are;
A is the area of a hexagona is the length of the side of the hexagon.From the information given,
Substitute the values, we have;
Area = 3√3/2 × 18²
Find the square
Area = 1. 73 ×324/2
Multiply the values
Area =560. 5/2
Divide the values
Area = 280. 26 square inches
Learn about polygons at: https://brainly.com/question/8409681
#SPJ1
Write an equation of the parabola in vertex form.

Answers
how many 8-letter ""words"" using the 26-letter alphabet (letters can be repeated) either begin or end with a vowel?
Answers
There are 26^7 * 21 number of ways to create an 8-letter word using the 26-letter alphabet that begins or ends with a vowel, where 26 is the number of letters in the alphabet, and 21 is the number of consonants.
To find the number of 8-letter words that either begin or end with a vowel, we need to consider two cases: words that begin with a vowel and words that end with a vowel.
For words that begin with a vowel, we have one vowel as the first letter and any of the 26 letters of the alphabet for the remaining 7 letters. Hence, there are 26^7 ways to create an 8-letter word that begins with a vowel.
For words that end with a vowel, we have 21 consonants for the first letter and any of the 26 letters of the alphabet for the remaining 7 letters, followed by one of the five vowels. Hence, there are 21 * 26^7 * 5 ways to create an 8-letter word that ends with a vowel.
Therefore, the total number of 8-letter words that either begin or end with a vowel is the sum of the two cases: 26^7 + 21 * 26^7 * 5, which simplifies to 26^7 * 21.
To know more about the number of ways refer here:
https://brainly.com/question/30649502#
#SPJ11
Someone pleaseee help I’m struggling

Answers
Step-by-step explanation:
(0,5) and (-2,-3)
y=mx+b
find m
\( \frac{y1 - y2}{x1 - x2} \\ = \frac{5 - ( - 3)}{0 - ( - 2)} \\ = \frac{8}{2} \\ = 4 \\ \)
m=4
Substitute (0,5) or (-2,-3)
For easy processing substitute : (0,5)
y=4x+b
5=b
y=4x+5 is the answer
Brainliest please~
A rectangle has side lengths 2x + 3 and 5x - 2.
Write an expression without brackets for the area of the rectangle
Answers
Answer:
10x² + 11x - 6
Step-by-step explanation:
The area (A) is the product of the sides, that is
A = (2x + 3)(5x - 2) ← expand using FOIL
= 10x² - 4x + 15x - 6 ← collect like terms
= 10x² + 11x - 6
PLEASEEE HELPPPP MEE WITH LINE PLOTSSS I DONT UNDERSTAND THISSSS
PLEASEE HELPPPP!!!!!!!


Answers
Answer:
Look at the lightest loaf of bread. It weighs 22 1/3 oz. The heavist loaf weighs 24 1/2. Subtract 24 1/2 and 22 1/3. Then, if the answer to that is 1 1/2 ounces then you agree. If it is not, then disagree. Then, add up all of the weights of the bread and find the answer.
plsxsssss helppp meee

Answers
The equation in standard form that models the number of possible t-shirts and shorts you can buy is; 4.5x + 6y = 108
The graph of the function is as attached
How to graph Linear Equation?
A linear equation is defined as an equation whereby the highest power of the variable is always 1.
We are told that the cost of each T-shirt is $4.50 while each short costs $6. Thus, if he has enough money for 12 t-shirts and 9 pairs of shorts, it means that;
Total amount he has = 12(4.5) + 9(6) = $108
Now, if the amount of t-shirts he can possibly buy is x and the amount of pairs of shorts he can possibly buy is y. Thus, the linear equation is;
4.5x + 6y = 108
Read more about Graph of Linear Equation at; https://brainly.com/question/14323743
#SPJ1

Two customers each both sets of tables and chairs for my furniture store offering a single price for chairs any single price for tables the amount paid by each customer is represented by the following any qualities where I see is the price of a single chair and tea is the price of a single table
Answers
PLEASE HELP ME
Answers that are possible:
A. –3 > |x + 1|
B. 1 > |x + 2| + 2
C. 2 < |x + 3| – 2
D. 4 > |x + 1| + 2

Answers
The inequality represented by the graph is given as follows:
D. 4 > |x + 1| + 2.
How to obtain the inequality represented by the graph?The solution set represented by the graph is composed by numbers between -3 and 1, with an open interval, that is:
-3 < x < 1.
Then we solve each inequality in this problem, to find the one with the solution set that matches this one.
For item a, we have that:
|x + 1| < -3.
Which has no solution, as the absolute value function always assumes a value of at least zero.
For item b, we have that:
1 > |x + 2| + 2.
|x + 2| < -1.
No solution, for the same reason as item a.
For item c, we have that:
2 < |x + 3| - 2
|x + 3| < 4.
Hence:
-4 < x + 3 < 4.
The lower bound of the solution is of:
x + 3 > -4
x > -7.
Which does not match.
For item d, we have that:
4 > |x + 1| + 2
|x + 1| < 2
Hence:
-2 < x + 1 < 2
The lower bound of the solution is of:
x + 1 > -2
x > -3.
The upper bound of the solution is of:
x + 1 < 2
x < 1.
Meaning that option D is the correct option.
More can be learned about inequalities at https://brainly.com/question/9290436
#SPJ1