(DONT JUST ANSWER FOR POINTS!!) A French toast recipe calls for 3/4 cup milk per beaten egg. An equivalent ratio to this rate is ___ cups milk for every ___ beaten eggs.
(choices)
4
3
Answers
Answer:
3,4
Step-by-step explanation:
The first blanck answer is 3 because 3/4 is also known as .75 as a decimal and if you do 3 divided by .75 you get 4 meaning 4 is your second black answer
Hope this Helped!!!
Answer:
French toast recipe calls for 3/4 cup milk per beaten egg. An equivalent ratio to this rate is 3 cups milk for every 4 beaten eggs.
Step-by-step explanation:
hope it helps brainliest would also be appreaciated
Related Questions
subtract the following 18 upon 25 -7 upon 5
Answers
Question:- Subtract :- \( \frac{18}{25} - \frac{7}{5} \)
Answer:-
\( \frac{18}{25} - \frac{(7)}{5} \\ \)
L.C.M -> 25
\( \frac{18 - 7(5)}{25} \\ \frac{18- 35}{25} \\ \frac{-17}{25} = -0.68 \)
a sculptor wants to remove stone from a cylindrical block that has a height of 3 feet to create a cone. the diameter of the base of the cone and cylinder is 2 feet. what is the volume of the stone that the sculptor must remove? round your answer to the nearest hundredth.
Answers
The sculptor must remove approximately 1.57 cubic feet of stone. Rounded to the nearest hundredth, this is 1.57 cubic feet.
To solve this problem, we need to use the formula for the volume of a cylinder and the volume of a cone. The volume of a cylinder is given by the formula V = πr^2h, where r is the radius of the base and h is the height of the cylinder.
The volume of a cone is given by the formula V = (1/3)πr^2h, where r is the radius of the base and h is the height of the cone.
In this case, we are given that the height of the cylindrical block is 3 feet and the diameter of the base is 2 feet. Since the diameter is 2 feet, the radius is 1 foot. Therefore, the volume of the cylindrical block is V = π(1)^2(3) = 3π cubic feet.
To create a cone from the cylindrical block, the sculptor needs to remove some stone. The diameter of the base of the cone is also 2 feet, so the radius is 1 foot.
We are not given the height of the cone, but we know that it must be less than 3 feet in order for the cone to fit inside the cylindrical block. Let's call the height of the cone h.
Using the formula for the volume of a cone, we can write the volume of the removed stone as V = (1/3)π(1)^2h = (1/3)πh. To find the height of the cone, we can use similar triangles.
The height of the cone is to the height of the cylinder as the radius of the cone is to the radius of the cylinder. Therefore, h/3 = 1/2, or h = 3/2 feet.
Plugging in the value of h, we get V = (1/3)π(1)^2(3/2) = π/2 cubic feet. Therefore, the sculptor must remove approximately 1.57 cubic feet of stone. Rounded to the nearest hundredth, this is 1.57 cubic feet.
To know more about value click here
brainly.com/question/30760879
#SPJ11
Suppose that A and B are events with P(A) = 0.5, P(B) = 0.1, and P(A and B) = 0.3. What is the probability that B will occur, if A occurs? Question 3 1 pts Suppose that A and B are events with P(A) = 0.3 and P(B) = 0.4. Furthermore, if A happens, then B must also happen. What is P(A or B)? O 0.3 O 0.4 O 0.58 O 0.7 O Not enough information given Question 4 1 pts Suppose that A and B are mutually exclusive, that P(A) = 0.7, and that P(B) = 0.2. Which of the following is true? O P(B|A) > P(B) O P(BIA) = P(B) O P(BIA) < P(B)
Answers
A and B are mutually exclusive, with P(A) is 0.7 and P(B) is 0.2, the probability of event B given event A (P(B|A)) and the probability of event B given event A (P(BIA)) are both 0.2.
To find the probability of B given A, we can use the formula:
P(B|A) = P(A and B) / P(A)
Given:
P(A) = 0.5
P(B) = 0.1
P(A and B) = 0.3
P(B|A) = 0.3 / 0.5
= 0.6
Therefore, the probability that B will occur if A occurs is 0.6.
Given:
P(A) = 0.3
P(B) = 0.4
Since A happening guarantees that B must also happen, the events A and B are not independent. In this case, we can use the formula:
P(A or B) = P(A) + P(B) - P(A and B)
P(A or B) = 0.3 + 0.4 - 0.3
= 0.4
Therefore, the probability of A or B occurring is 0.4.
Given:
P(A) = 0.7
P(B) = 0.2
Since A and B are mutually exclusive events, they cannot occur together. In this case, we have:
P(A and B) = 0
Therefore, P(B|A) = P(BIA)
= 0.
P(BIA) = P(B)
= 0.2.
So, P(BIA) < P(B) is true.
When events A and B are mutually exclusive, with P(A) = 0.7 and P(B)
= 0.2, the probability of event B given event A (P(B|A)) and the probability of event B given event A (P(BIA)) are both 0.2.
To know more about probability, visit:
https://brainly.com/question/23417919
#SPJ11
HELP PLEASEEEE AND EXPLAIN

Answers
The probability that the sum of the throw is divisible by 4 but greater than 7 is 17 / 36.
How to find the probability ?There are 36 possible outcomes when two dice are tossed.
The sum of the dice can be any number from 2 to 12. The sum is divisible by 4 when the sum is 4, 8, or 12. The sum is greater than 7 when the sum is 8 , 9 , 10 , 11, or 12.
There are 3 ways to get a sum of 4, 3 ways to get a sum of 8, 2 ways to get a sum of 12, 4 ways to get a sum of 9, 4 ways to get a sum of 10, and 1 way to get a sum of 11.
The probability of getting a sum that is divisible by 4 or greater than 7 is:
= ( 3 + 3 + 2 + 4 + 4 + 1 ) / 36
= 17 / 36
Find out more on probability at https://brainly.com/question/23955312
#SPJ1
Can someone help me with this pleaseee…….

Answers
The sides of the quadrilateral arranged from longest to shortest are CD, AB, DA, and BC.
We have,
To arrange the length of the sides of the quadrilateral from longest to shortest, we need to calculate the length of each side of the quadrilateral using the distance formula:
Distance Formula:
If (x1, y1) and (x2, y2) are two points in a plane, then the distance between them is given by:
d = √((x2 - x1)² + (y2 - y1)²)
Using the distance formula, we can calculate the length of each side of the quadrilateral as follows:
AB = √((4 - (-5))² + (5 - 5)²) = 9
BC = √((2 - 4)² + (0 - 5)²) = √(29)
CD = √((-5 - 2)² + (-2 - 0)²) = √(74)
DA = √((-5 - (-5))² + (5 - (-2))²) = 7
Therefore,
The sides of the quadrilateral arranged from longest to shortest are CD, AB, DA, and BC.
Learn more about quadrilaterals here:
https://brainly.com/question/29934440
#SPJ1
Evaluate x−2 for x=−3

Answers
Answer:
1/9
Step-by-step explanation:
x^-2
We know that a^-2 = 1/ a^2
1/x^2
Let x = -3
1/ (-3)^2
1/9
1/9 is a required answer.
Answer:
solution given:
\(x^{-2}=\frac{1}{x²}\)
again
substituting value of x
we have (-3)²=9
now
\(\bold{\frac{1}{x²}=\frac{1}{9}}\)
A window is 12 feet above the ground. A ladder is placed on the ground to reach the window. If the bottom of the ladder is placed 5 feet away from the ladder building, what is the length of the ladder
Answers
Answer:
Therefore, the length of the ladder is 13 feet.
Step-by-step explanation:
This is a classic example of a right triangle problem in geometry. The ladder serves as the hypotenuse of the triangle, while the distance from the building to the ladder and the height of the window serve as the other two sides. Using the Pythagorean theorem, we can solve for the length of the ladder:
ladder^2 = distance^2 + height^2 ladder^2 = 5^2 + 12^2 ladder^2 = 169 ladder = √169 ladder = 13
Therefore, the length of the ladder is 13 feet.
brainliest PLssssss
lines c and d are parallel. which statement about the relationship between the angle measures are true?
Answers
The statement which is true by the corresponding angles theorem is option (B) ∠2 ≅ ∠6
The corresponding angles theorem states that when a transversal intersects two parallel lines, the pairs of corresponding angles are congruent.
In this case, lines c and d are parallel and transversal p intersects them, creating eight angles: ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, and ∠8.
The corresponding angles are
∠1 and ∠5
∠2 and ∠6
∠3 and ∠7
∠4 and ∠8
Since lines c and d are parallel, we know that ∠2 and ∠6 are corresponding angles. Therefore, by the corresponding angles theorem, we can conclude that ∠2 ≅ ∠6
Therefore, the correct option is (B) ∠2 ≅ ∠6
Learn more about corresponding angles theorem here
brainly.com/question/19562895
#SPJ4
The given question is incomplete, the complete question is:
Lines c and d are parallel lines cut by transversal p.
Which must be true by the corresponding angles theorem?
A) ∠1 ≅ ∠7
B) ∠2 ≅ ∠6
C) ∠3 ≅ ∠5
D) ∠5 ≅ ∠7

An electric car's home battery charger uses 10.7 kiloWatt for 6 hour. If electricity costs $0.46 per kiloWatt-hour, how much (in dollars, to the nearest penny) does it cost to charge the car's battery
Answers
For an electric car's home battery charger uses 10.7 kiloWatt for 6 hour, the total cost of electricity used by it is equals to the $29.532.
We have an electric car's home battery charger. The amount of power used by charger, P = 10.7 kilowatt
Time taken by charger to use power of 10.7 kilowatt, t = 6 hours
The rate of cost of electricity, r = $0.46 per kilowatt - hour
We have to determine the cost to charge the car's battery. Now, first we calculate the total energy used for charging, E= P × t
=> E = 10.7 kilowatt × 6 hours
= 64.2 kilowatt- hour
Also, Total cost of electricity = E × r
= 0.46 per kilowatt- hour × 64.2 kilowatt- hour
= $ 0.46 × 64.2
= $ 29.532
Hence, required value is $29.532.
For more information about total cost, visit:
https://brainly.com/question/25109150
#SPJ4
f(x) = 3x + k
f(4) = 10
easy equation but I just need a confirmation that the answer is actually -2 lol
Answers
Answer:
-2
Step-by-step explanation:
f(x) = 3x + k
f(4) = 10
f(4) = 3×4+k
10 = 12 + k
10-12 = k
k = -2
(-7s + 4) - (-8s + 4)
Answers
Answer:
s
General Formulas and Concepts:
Pre-Algebra
Distributive PropertyAlgebra I
TermsStep-by-step explanation:
Step 1: Define
(-7s + 4) - (-8s + 4)
Step 2: Simplify
Distribute negative: -7s + 4 + 8s - 4Combine like terms (s): s + 4 - 4Combine like terms (Z): sMichael’s child is going to college in 13 years. If he saves $ 7,000 a year at 9%
compounded annually. How much will be available for Peter’s child education?
Answers
Michael’s child is going to college in 13 years. If he saves $ 7,000 a year at 9% compounded annually. Therefore, the amount available for Peter's child education will be $147,330.55.
Given that Michael is saving $7,000 per year for his child's education which will occur in 13 years. If the interest rate is 9% compounded annually,
The problem of finding the amount of money Michael will have saved in 13 years is a compound interest problem.
In this case, the formula for calculating the future value of the annuity is: $FV = A[(1 + r)n - 1] / r
where: FV is the future value of the annuity, A is the annual payment,r is the annual interest rate, and n is the number of payments.
Using the above formula; the future value of Michael's savings is:
FV = 7000[(1 + 0.09)^13 - 1] / 0.09= 7000(1.09^13 - 1) / 0.09= 147,330.55
Therefore, the amount available for Peter's child education will be $147,330.55.
Learn more about interest rate here:
https://brainly.com/question/27743950
#SPJ11
1. For the geometric series 0. 5 -0. 1 + 0. 2. Sn= 0. 416. Find thenumber of terms in the series. 2. For a geometric progression, u3= 4. 5 and u7= 22. 78125. Findthe value of the common ratio and the
Answers
Answer:
The common ratio would be 8:1.
Is t = –2 a solution to the inequality below?
–1 ≤
t
yes or no
Answers
Hope this helped
Divide the polynomial by the binomial with or without remainder
(y^(2)-5y+4)÷(y-4)
Answers
Answer:
(y-1)
Step-by-step explanation:
simplified you split y^2-1y+-4y+4 this is further simplified by splitting equation into y(y-1) -4(y-1) this leaves you with (y-4)(y-1)/(y-4) y-4 will cancel out and you are left with y-1
What is an equation of the line that passes through the points (-3,-1) and (6,2)?
Answers
Answer:
\(y=\frac{1}{3}x\)
Step-by-step explanation:
Hi there!
Linear equations are typically organized in slope-intercept form: \(y=mx+b\) where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
1) Determine the slope (m)
\(m=\frac{y_2-y_1}{x_2-x_1}\) where two points the line passes through are \((x_1,y_1)\) and \((x_2,y_2)\)
Plug in the given points (-3,-1) and (6,2)
\(=\frac{2-(-1)}{6-(-3)}\\=\frac{2+1}{6+3}\\=\frac{3}{9}\\=\frac{1}{3}\)
Therefore, the slope of the line is \(\frac{1}{3}\). Plug this into \(y=mx+b\):
\(y=\frac{1}{3}x+b\)
2) Determine the y-intercept (b)
\(y=\frac{1}{3}x+b\)
Plug in one of the given points and solve for b
\(2=\frac{1}{3}(6)+b\\2=2+b\)
Subtract 2 from both sides to isolate b
\(2-2=2+b-2\\0=b\)
Therefore, the y-intercept is equal to 0. Plug this back into \(y=\frac{1}{3}x+b\):
\(y=\frac{1}{3}x+0\\y=\frac{1}{3}x\)
I hope this helps!
Find the value of z.

Answers
2z = 15
z = 7.5
How else can the sequence for Row 1 be written? Notice: Square A: 1 penny = 20 Square B: 2 pennies = 21 Square C: 4 pennies = 22 How many pennies would be on the square labeled H? 29 28 27.
Answers
Answer:
2^7
Step-by-step explanation:
2 to the power of 7
There are 27 pennies on the square labeled H
What is a sequence?A sequence is a collection of numbers or character that follow the same pattern or rule
From the question, we have:
Square A: 1 penny = 20
Square B: 2 pennies = 21
Square C: 4 pennies = 22
So, the sequence can be written as:
\(T_n = n + 19\)
Where n represents the square number
For a square labelled H, we have:
n = 8
So, the number of pennies is:
\(T_8 = 8 + 19\)
\(T_8 = 27\)
Hence, there are 27 pennies on the square labeled H
Read more about sequence at:
https://brainly.com/question/7882626
What is the sum of the interior angles of an octagon?
Answers
Answer:
1080 degrees
180(n-2) = sum of all interior angles
180(6) = 1080
Answer:
1080°
Step-by-step explanation:
What is the angle sum of Octagon?
1080°
The sum of all the internal angles of any octagon is 1080°. As with all polygons, the external angles total 360°.
A=2(1+2)a2 this is the formula
Can someone help me with Geometry?

Answers
Answer:
6x + 2 is your answer I THINK
A plot of land is for sale. A scale drawing of the land shows the distance between the house and a barn as 4.8 cm. If the drawing uses a 1/800 scale factor what is the actual distance in meters between the house and the barn?
Answers
Answer:
If the scale factor is 1/800, it means that 1 cm on the scale drawing represents 800 cm or 8 meters in real life.
So, to find the actual distance between the house and the barn, we need to convert the distance on the scale drawing (4.8 cm) to meters and then multiply by the scale factor:
Actual distance = (Distance on scale drawing in cm) x (Conversion factor)
where the conversion factor is:
Conversion factor = (1 cm) / (100 cm/m) = 0.01 m/cm
Plugging in the values, we get:
Actual distance = (4.8 cm) x (0.01 m/cm) x (8 meters/1 cm) = 0.384 meters
Therefore, the actual distance between the house and the barn is 0.384 meters.
I'M TERRIBLE AT MATH SOMEONE HELP, WILL GIVE BRAINLIEST

Answers
Answer:
D) -1.8, -1 1/2 , 0.3 , 3/4 , 1
Step-by-step explanation:
Change all of the given terms to either fractions or decimals. Generally decimals are easier:
3/4 = 0.75
-1.8 = -1.8
1 = 1.0
-1 1/2 = -1.5
0.3 = 0.3
Order from least to greatest:
-1.8 , -1.5, 0.3 , 0.75 , 1.0
or
-1.8, -1 1/2 , 0.3 , 3/4 , 1
~
What is the equation of the line that passes through the point (-6.-2) and
has a slope of -1/6
Answers
the answer is y= -x\2-1
Answer:
y=-1/6x-3
Step-by-step explanation
1 step is substituting, which makes -2=-1/6(-6)+b
2 it become -2=1+b
3 Then subtracting 1 form both sides you get -3=b
4 then put it into slope form making it y=-1/6x-3
A flag post that is 40 ft in height casts a shadow that is 25 ft in length, if a nearby building is 200 ft talk what is the length of the flag pole
Answers
Answer:
I would assume that the shadow length is proportional to the height of the flagpole. Hence as the building is 5 times higher than the flagpole, the length of the shadow would be 5 times higher, 25x5= 125 ft.
Step-by-step explanation: hope this helps have a wonderful day :D
A website charges $3 for each movie you download. They also charge a one-time sign-up fee of $14. 99. What is the input variable?.
Answers
Answer:
The input variable is 5 i.e 15/3
A student needs 15 minutes to solve an algebra problem how many minutes dose this student need to slove 5 problems?
Answers
Answer:
75 minutes or 1 hour and 15 minutes
Step-by-step explanation:
15·5=75
Answer:
3 min's per question
Step-by-step explanation:
Mrs. Taylor bought some oranges and 30% of them were bad. Of there were 60 bad oranges how many oranges did she buy? *NEED ANSWER ASAP(Under 2 days)*
Answers
Answer:
Mrs. Taylor bought 200 oranges ;) .
Answer:
200
Step-by-step explanation:
If 30% of the oranges were bad, then that means 0.3 * total number of oranges, were bad. so if 0.3 * total = 60, then 60/0.3 = total number of oranges.
Sasha practices piano for 45 minutes, 6 days a week. How many minutes does Sasha practice in a week? Use an area model to solve.
Answers
Answer:
270
Step-by-step explanation:
Because i multiple 45 by 6
ANSWER ASAP PLEASE PICTURE BELOW

Answers
can you please explain it more clearly
Step-by-step explanation:
ABCD is a rectangle. Find the mCED
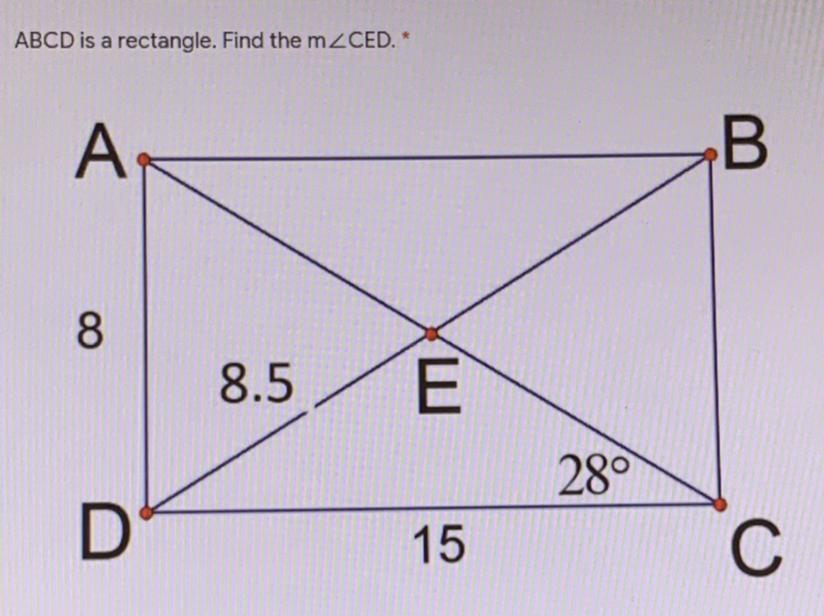
Answers
Answer:8.5...
Step-by-step explanation: