During the last football season, the percentage of tight ends in the league who made a touchdown reception was 45%. A sports statistician is interested in how the spread of receptions is affected by sampling a different number of tight ends in the league. What is the standard error of the sampling distribution of sample proportions for samples of size n= 32, n=42 and n=52?
Answers
The standard error of the sampling distribution for n = 32 is 0.0850, n= 42 is 0.014 and n = 52 is 0.009.
The standard error of the sampling distribution of sample proportions for samples of size.
To calculate the standard deviation (σ) of the population proportion, which is given by:
for n = 32
σ = \(\sqrt{[p * (1-p) / n]}\)
\(\sqrt{ [0.45 * (1-0.45) / 32]}\) = 0.0805
SE = σ/ \(\sqrt{(32)}\) = 0.0143
For n = 42:
σ = \(\sqrt{ [0.45 * (1-0.45) / 42] }\) = 0.0739
SE = σ / \(\sqrt{n}\) = 0.0739 / \(\sqrt{42}\) = 0.0114
For n = 52:
σ = \(\sqrt{{ [0.45 * (1-0.45) / 52]}}\) = 0.067
SE = σ/\(\sqrt{n}\) = 0.067/\(\sqrt{52}\) = 0.0094
Therefore, the standard error for n = 32 is 0.0850, n= 42 is 0.014 and n = 52 is 0.009 rounded to the nearest hundredths.
Learn more about standard error of the sampling distribution
brainly.com/question/14467769
#SPJ4
Related Questions
2. Use mathematical induction to show that n(n+1)(2n+1) is divisible by 6 for all positive integers n.
Answers
The given statement: n(n+1)(2n+1) is divisible by 6 for all positive integers n.
Step-by-step explanation: We need to prove that n(n+1)(2n+1) is divisible by 6 for all positive integers n using mathematical induction.
Step 1: First, lets prove the statement for the smallest possible value of n. The smallest value of n is 1. So, let's check whether the given statement is true for n = 1 or not.
\(LHS = 1(1+1)(2*1+1) = 6\)
It is divisible by 6. Hence, the statement is true for n=1.
Step 2: Let's assume that the statement is true for n=k. So, we can say that n(n+1)(2n+1) is divisible by 6 for n=k. i.e., n(n+1)(2n+1) = 6a (for some integer a).
Step 3: We need to prove the statement is true for n=k+1.
So, we need to prove that (k+1){(k+1)+1}[2(k+1)+1] is divisible by 6
Using the assumption we made in step 2.
\(LHS = (k+1){(k+2)}[2k+3] = (k+1)(k+2)(2k+3)LHS = (2k+3)k(k+1)(k+2)LHS = 2[k(k+1)(k+2)] + 3[k(k+1)]\)
Now, k(k+1)(k+2) is divisible by 6 using the assumption made in step 2.
So, LHS = 2[k(k+1)(k+2)] + 3[k(k+1)] is also divisible by 6.
Hence, the statement is true for n=k+1.
Step 4: Using steps 1 to 3, we can say that the given statement is true for n=1 and if it is true for n=k, then it is also true for n=k+1.
Hence, by mathematical induction, we can say that the statement is true for all positive integers n.
Hence, it is proved that n(n+1)(2n+1) is divisible by 6 for all positive integers n.
To know more about mathematical induction visit :
https://brainly.com/question/29503103
#SPJ11
Find the volume of radius 7 cm in diameter of 12 cm in 3.14
Answers
The volume of a sphere with a radius of 7 cm (or diameter of 12 cm) is 904.32 cubic centimeters.
To find the volume of a sphere with a radius of 7 cm, we can use the formula:
V = (4/3) * π * r^3
where V represents the volume and r represents the radius. However, you mentioned that the diameter of the sphere is 12 cm, so we need to adjust the radius accordingly.
The diameter of a sphere is twice the radius, so the radius of this sphere is 12 cm / 2 = 6 cm. Now we can calculate the volume using the formula:
V = (4/3) * π * (6 cm)^3
V = (4/3) * 3.14 * (6 cm)^3
V = (4/3) * 3.14 * 216 cm^3
V = 904.32 cm^3
For more such questions on volume
https://brainly.com/question/463363
#SPJ8
What is the value of X? WILL GIVE BRAINLIEST!

Answers
Answer:
18
Step-by-step explanation:
2 congruent triangles, their respective sides are congruent so:
(2x+80)/(27+60)= 80/602x+80= 87*4/32x+80= 1162x= 36x=18Write an equation in point-slope form of the line that passes through the given point and has the given slope (4, -5); m = 6
Answers
Answer:
m=6
X1=4
Y1= -5
Y-Y1=m(X-X1)
Y-(-5)=6(X-4)
Y+5=6X-24
Y=6X-24-5
Y=6X-29
consider the poset ({2, 4, 5, 10, 20}, |). what are the maximal elements, the minimal elements, the greatest element, and the least element of the poset?
Answers
Maximal elements are 10 and 20, minimal elements are 2 and 4, there is neither greatest element and nor least element.
→ The maximal element in the poset is an element that is divisible by all elements in poset is comparable to. so 10 and 20 are the maximal elements.
→The minimal element in the poset is an element that is divisible by all other elements in the relation they are comparable to. so 2 and 4 are minimal elements.
→There is no greatest element because 10 and 20 are incomparable which means that one doesn't precede the other.
→There is no least element because 2 and 4 are incomparable which means that one doesn't precede the other.
The equation A equals P equals quantity 1 plus 0.07 over 4 end quantity all raised to the power of 4 times t represents the amount of money earned on a compound interest savings account with an annual interest rate of 7% compounded quarterly. If after 15 years the amount in the account is $13,997.55, what is the value of the principal investment? Round the answer to the nearest hundredths place.
$13,059.12
$10,790.34
$9,054.59
$4,942.96
Answers
The value of the principal investment is:
$4,942.96
How to find the value of the principal investment?
To determine the value of the principal investment, we can use the given compound interest formula:
\(A = P(1 + \frac{0.07}{4})^{4t}\)
Where:
A = the final amount after 15 years
P = the principal
0.07 = the interest rate (7%)
4 = the number of times the interest is compounded per year, in this case quarterly
t = the time period in years, 15
Substituting t and A into the formula, we can find P:
\(13,997.55 = P(1 + \frac{0.07}{4})^{4*15}\)
\(13,997.55 = P(1 + 0.0175)^{60}\)
\(13,997.55 = P(1.0175)^{60}\)
\(P = \frac{13,997.55}{(1.0175)^{60}}\)
P = $4,942.96
Learn more about compound interest on:
brainly.com/question/24274034
#SPJ1
A cylinder has a height of 13 meters. Its volume is 16,328 cubic meters. What is the radius of the cylinder
Answers
Answer:
19.99 (rounded)
Step-by-step explanation:
We know that the formula to solve is:
\(V=\pi r^{2}h\).
\(R = \sqrt{\frac{V}{\pi h } } = \sqrt{\frac{16328}{\pi 13} = 19.99493\)
what is the ratio ηf/ηi, where ηf is the final surface charge density?
Answers
The ratio of the final surface charge density (ηf) to the initial surface charge density (ηi) is given by 3.68 * \(Q_i / (A_i \times A_i).\)
To understand the concept and solve this problem, we need to consider the relationship between surface charge density, area, and charge. Surface charge density (σ) is defined as the charge (Q) per unit area (A). Mathematically, we can express this relationship as σ = Q/A.
Let's assume the initial area of the irregular shape is \(A_i\), and the final area after each dimension is reduced is \(A_f\). Since each dimension (x and y) is reduced by a factor of 3.68, we can write the relationship between the initial and final areas as:
\(A_f = (1/3.68) \times A_i\)
Now, let's consider the relationship between charge and area. Since the charge remains constant for a given area, we can express it as \(Q_i = Q_f\), where \(Q_i\) is the initial charge and \(Q_f\) is the final charge.
Since the charge remains constant, the ratio of the surface charge densities can be expressed as:
ηf/ηi = \(\sigma _f/\sigma _i = Q_f/A_f / Q_i/A_i\)
Substituting the expressions for area into the equation, we have:
ηf/ηi = \(Q_f/A_f / Q_i/A_i = Q_f / (A_f * Q_i) * (A_i / Q_i)\)
Canceling out the \(Q_i\) terms, we get:
ηf/ηi = \(Q_f / (A_f * Q_i) * (A_i / Q_i) = Q_f / (A_f * A_i)\)
Since \(Q_i = Q_f\), we can simplify further:
ηf/ηi = \(Q_f / (A_f * A_i) = Q_i / (A_f * A_i)\)
Now, substituting the expressions for area into the equation, we have:
ηf/ηi = \(Q_i / (A_f * A_i) = Q_i / ((1/3.68) * A_i * A_i)\)
Simplifying, we find:
ηf/ηi = 3.68 x \(Q_i / (A_i \times A_i).\)
To know more about ratio here
https://brainly.com/question/13419413
#SPJ4
Complete Question:
The irregularly shaped area of charge in the figure has surface charge density ηi. Each dimension (x and y) of the area is reduced by a factor of 3.68.
What is the ratio ηf/ηi where ηf is the final surface charge density?
Which linear function has the steepest slope? Whoever answers this first I will mark them brainless

Answers
Answer:
y=-8x+5
Step-by-step explanation:
The others have a slope of -2, 7, and 6, which is not as steep as -8.
Answer:
A) y = -8x + 5
Step-by-step explanation:
Just took the test!
Correct me if I'm wrong!
Thank you
Tisa B Sora
please tell me answers

Answers
Answer:
no 8 is 90° and no 9 is two
Step-by-step explanation:
90° and two circles can pass through a given point
Find the surface area of a regular hexagonal pyramid with side length = 8, and a slant height = 16. Round to the nearest tenth.
Answer Immediately
Answers
Answer:
To find the surface area of a regular hexagonal pyramid, we need to find the area of the six triangular faces and the area of the hexagonal base, and then add them together.
The area of each triangular face is given by the formula:
(1/2) x base x height
In this case, the base of each triangle is the side length of the hexagon (8), and the height is the slant height of the pyramid (16). Therefore, the area of each triangular face is:
(1/2) x 8 x 16 = 64
The hexagonal base can be divided into six equilateral triangles, each with side length 8. The area of each equilateral triangle is:
(1/4) x sqrt(3) x side length^2
Plugging in the values, we get:
(1/4) x sqrt(3) x 8^2 = 16sqrt(3)
To find the total surface area, we add the area of the six triangular faces and the area of the hexagonal base:
6 x 64 + 16sqrt(3) = 384 + 16sqrt(3)
Rounding to the nearest tenth, the surface area of the regular hexagonal pyramid is:
398.6 square units (rounded to one decimal place)
Is it A,B,C or D I´m stuck on this..

Answers
Answer d
Step-by-step explanation:d
Answer:
c. 51
Step-by-step explanation:
Answer these two and I'll make as brainest.

Answers
Answer:
25x + 5 equals 130, x=5, (2) x= 6 10x=60 degrees
Step-by-step explanation:
Tell whether the function
\(y - 4x {}^{2} = 3 x\)
linear or nonlinear
Answers
please help meeeeee for points

Answers
Answer: Choice C
XY < YZ < ZX
=================================================
Explanation:
Check out the diagram below
Angle X = 70
Angle Y = 88
Z is the unknown angle. The three angles of any triangle always add to 180
X+Y+Z = 180
70+88+Z = 180
Z+158 = 180
Z = 180-158
Z = 22
Angle Z is 22 degrees.
Since Z is the smallest angle, this means the side opposite that is the smallest side. The smallest angle is always opposite the smallest side, and vice versa. So XY is the smallest side.
The largest side is always opposite the largest angle. Here we have angle Y = 88 as the largest, so side ZX is the largest side.
The order of the sides from smallest to largest is
XY < YZ < ZX

Stefan’s family rented a rototiller to prepare an area in their backyard for spring planting. The rental company charged an initial fee of $43 with an additional fee per hour. If they paid $64 after renting the rototiller for 7 hours, what was the hourly fee? If h represents the hourly fee, which equation models this problem? What was the hourly fee for the rototiller?
Answers
Answer:
It is $3.00 per hour
Step-by-step explanation:
Let C be the total charge and t be the rental time in hours.
C = ht + 43
Plugging the given values into the equation, we get:
64 = 7h + 43
7h = 21
h = 3
The hourly fee is $3.00 per hour.
The hourly fee for the rototiller is 3 dollars.
What is an equation?In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.
The solution of an equation is the set of all values that, when substituted for unknowns, make an equation true.
Given that, the rental company charged an initial fee of $43 with an additional fee per hour.
They paid $64 after renting the rototiller for 7 hours
Here, h represents the hourly fee
Now, 43+7h=64
7h=64-43
7h=21
h=$3
Therefore, the hourly fee for the rototiller is 3 dollars.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ7
PLEASE HELP ASAPPP !! WILL GIVE BRAINLIEST AND 5 STAR RATINGGG
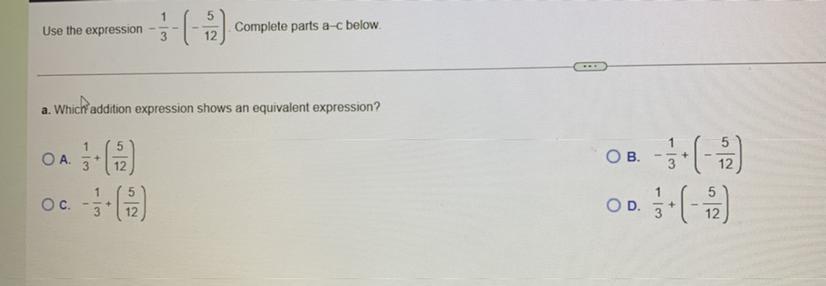
Answers
Answer: C
Step-by-step explanation:
A negative times a negative equals a positive.
For a fraction to a be Rational Number it has to be made up of _____?1. Integers2. Rational numbers3. Letters4. Irrational numbers
Answers
The definition of a rational number is: A rational number is a number that is of the form p/q where p and q are integers and q is not equal to 0.
Examples of rational numbers are:
\(\frac{1}{2},\frac{2}{3},\frac{7}{8},\text{ etc}\)From the above definition
For a fraction to a be Rational Number it has to be made up of integers
The answer is option 1
PLEASE ANSWER !!!!!!!!!!!

Answers
Answer:
1 1/16
explanation:
its 1/16 of a pound because its half a serving and a serving is 1/8 of a pound
According to a certain country's Department of Education, 41.5% of three-year-olds are enrolled in daycare. what is the probability that a randomly selected three-year-old is daycare? a. 0.415 b. 0.585 c. 42 d. There is no way to tell since the probability of selecting a three-year-old in daycare is unrelated to the proportion of three-year-olds in daycare.
Answers
The correct answer is option A: 0.415.The probability that a randomly selected three-year-old is in daycare is 0.415. This is because the given information tells us that 41.5% of three-year-olds are enrolled in daycare.
Option A: 0.415 is the right answer.The likelihood of a randomly picked three-year-old being in creche is 0.415. This is due to the fact that 41.5% of three-year-olds are enrolled in nursery, according to the data.
Because a randomly chosen three-year-old can be in creche or not, the likelihood that a randomly chosen three-year-old is in creche is the same as the proportion of three-year-olds enrolled in creche, which is 0.415, or 41.5%.
To elaborate, probability is a measure of the possibility that an event will occur. It is usually a number between 0 and 1, with 0 indicating that the occurrence is impossible and 1 indicating that the event is unavoidable.
In this scenario, the event is picking a three-year-old who is enrolled in creche, with a chance of 0.415, or 41.5%, of this event occuring.
Therefore, the correct answer is option A: 0.415.
For more question on probability
https://brainly.com/question/25839839
#SPJ8
Find the value of x that makes u and v parallel. Please help me!!
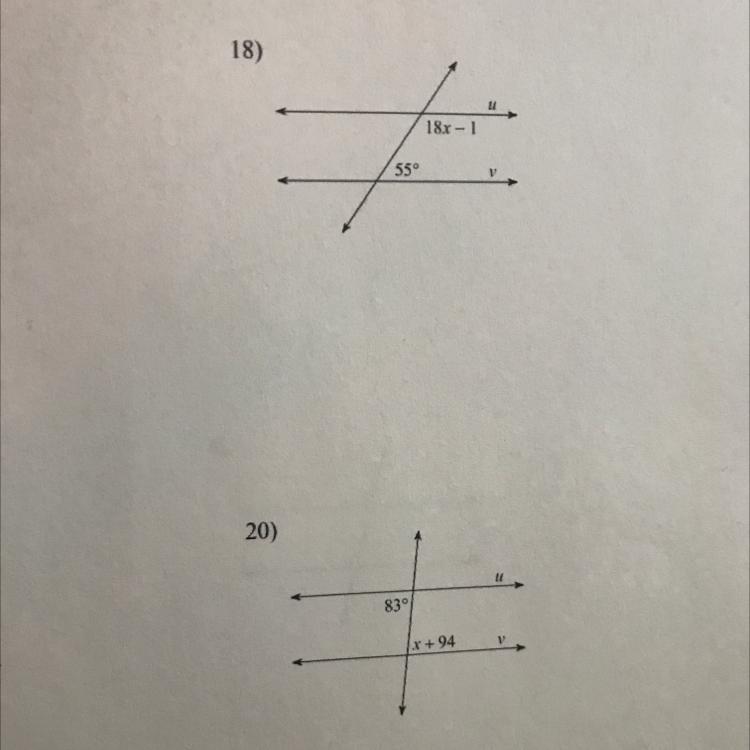
Answers
Answer:
7
Step-by-step explanation:
double the other angle 55 * 2 = 110
360 - 110 = 250 subtract from full circle of degrees
250/2 = 125 divide remainder by two
18x - 1 = 125
x = 7
What is the area of the triangle?

Answers
Answer:
63
Step-by-step explanation:
If m∠B = 46°, and m∠D = 67°, what is m∠BEA?
67°
46°
88°
134°

Answers
Is 16 a perfect square? Explain.
Answers
16 is a perfect square
Explanation:16 = 2 × 2 × 2 × 2
16 = (2 × 2) × (2 × 2)
16 = 4 × 4
Perfect squares numbers whose squares are whole numbers. Square root of 16 gives 4.
Hence, 16 is a perfect square
F(x)=4x+6, g(x) = 2x^2 find (fg) (x)
Answers
Answer:
F(2x^2) = 8x^2 + 6
Step-by-step explanation:
F (g(x))
= F(2x^2) = 4 (2x^2) + 6
= F(2x^2) = 8x^2 + 6
In a month, Caleb can produce a maximum of either 30 bushels of pears or 15 bushels of apples, or any linear combination in between. Similarly, Donna can produce a maximum of either 24 bushels of pears or 6 bushels of apples, or any linear combination in between. 1st attempt Part 1 (2 points) What is the opportunity cost for Caleb to produce one more bushel of apples in terms of pears
Answers
The opportunity cost for Caleb to produce one more bushel of apples in terms of pears is 2 bushels of pears.
To determine the opportunity cost for Caleb, we need to compare the trade-off between producing apples and pears. The given information states that Caleb can produce a maximum of 30 bushels of pears or 15 bushels of apples in a month.
We can calculate the opportunity cost by dividing the change in the quantity of pears by the change in the quantity of apples. In this case, if Caleb produces one more bushel of apples, he would have to give up producing pears. Therefore, the opportunity cost can be calculated as follows:
Opportunity Cost = Change in Pears / Change in Apples
Opportunity Cost = 30 bushels - 0 bushels / 15 bushels - 0 bushels
Opportunity Cost = 30 bushels / 15 bushels
Opportunity Cost = 2 bushels of pears per bushel of apples
The opportunity cost for Caleb to produce one more bushel of apples in terms of pears is 2 bushels of pears. This means that if Caleb decides to produce one additional bushel of apples, he would have to give up producing 2 bushels of pears.
To know more about opportunity cost follow the link:
https://brainly.com/question/28211220
#SPJ11
Homework please help

Answers
Answer:
b. one solution
Step-by-step explanation:
hope this helps :)
Answer:
B. One solution
Step-by-step explanation:
Hope this helps!!
find the area of the region that is bounded by the given curve and lies in the specified sector. r = 9 cos(), 0 ≤ ≤ /6
Answers
The area of the region bounded by the curve r = 9cos(θ) and the sector 0 ≤ θ ≤ π/6 is \($27\pi/8 - 81/8\times \sqrt{3}$\)
The curve r = 9cos(θ) is a polar curve that forms a half-circle with a radius of 9/2. To find the area of the region bounded by this curve and the sector 0 ≤ θ ≤ π/6, we can use the formula for the area of a polar region:
\($A = \frac{1}{2} \int_{a}^{b} r(\theta)^2 d\theta$\)
In this case, a = 0 and b = π/6, and the curve is given by r(θ) = 9cos(θ). Substituting these values into the formula, we get:
\($A = \frac{1}{2} \int_{0}^{\frac{\pi}{6}} (9\cos(\theta))^2 d\theta$\)
Simplifying and evaluating the integral gives:
\(A = \frac{1}{2} \int_{0}^{\frac{\pi}{6}} 81\cos^2(\theta) d\theta\\\\ = \frac{1}{2}\left(\frac{81}{2}\cdot\frac{\pi}{6}+\frac{81}{4}\cdot\sin\left(\frac{\pi}{6}\right)\right)\\ \\ = \frac{27\pi}{8} - \frac{81}{8}\sqrt{3}\)
Therefore, the area of the region bounded by the curve r = 9cos(θ) and the sector 0 ≤ θ ≤ π/6 is \($27\pi/8 - 81/8\times \sqrt{3}$\)
Learn more about polar curve here:
https://brainly.com/question/1094340
#SPJ11
Lmk if you understand thanks

Answers
Answer:
y = 100,000 (1 + 0.04) ²⁰
Step-by-step explanation:
Here:
100,000 = original amount.
0.04 = rate (a percent)
and
20 = number of times you need to run the simulation.
Abowling team consists of 34 members and 18 are male if 4females leaves the team ,what percent off the remaining number are male
Answers
after 4 females leave the team, the percentage of remaining team members who are male is 60%.
Initially, the team has 34 members with 18 males and 34 - 18 = 16 females. If 4 females leave the team, the number of females becomes 16 - 4 = 12. The number of remaining team members is 34 - 4 = 30 (since 4 members left).
To calculate the percentage of remaining team members who are male, we divide the number of males (18) by the total number of remaining team members (30) and multiply by 100:
Percentage of remaining team members who are male = (18 / 30) * 100 = 60%
Therefore, after 4 females leave the team, the percentage of remaining team members who are male is 60%.
learn more about percentage of remaining here:
https://brainly.com/question/13417121
#SPJ11