Elizabeth won a $300 gift certificate at silver gym. A membership costs $15 a month and has a one- time fee of $50. Complete the equation that models the number of months,x, her gift certificate is will pay for a Silver gym.

Answers
The correct answer is 15 x + 50 = 300
Explanation:
In an equation, the different values show a specific mathematical relationship, and the equality represented by the symbol (=) is used to find an unknown value. In the case presented, the unknown value is the number of months Elizabeth can pay using her $300 gift certificate. This means the letter x in the equation represents the number of months.
Moreover, this x should be multiplied by the month membership or $15 considering Elizabeth will need to pay this fee each month and this should be added to the one-time fee of $50. This implies the first part of the equation is 15x + 50. Finally, this value should be equal to the total money in the certificate or 300. According to this, the equation is 15x + 50 = 300.
Related Questions
Help solve for the area

Answers
Answer:
B
Step-by-step explanation:
half × base × height
height × length
Answer: B
Step-by-step explanation:
Triangle)
25 - 7 = 18
\(A=\frac{1}{2}(b)(h)\\A=\frac{1}{2}(18)(17)\\A=153cm^2\)
Rectangle)
\(A=b(h)\\A=7(17) = 119cm^2\)
Total)
\(153+119=272 cm^2\)
If m∠4=125° , what are the measures of ∠5 , ∠6 , ∠7 , and ∠8 ?

Answers
Answer: angle 5 = 55 degrees, angle 6 = 125 degrees, angle 7 = 55 degrees, angle 8 = 125 degrees
Suppose ln x-ln y=y-4 , where y is a differentiable function of x and y=4 when x=4 . What is the value of dy/dx when x=4 ?
Answers
Answer:
When x=4, ln x-ln y=y-4, so ln 4-ln 4=4-4, which is true. Therefore, when x=4, y=4, and dy/dx=0.
Step-by-step explanation:
So, when x = 4, the value of the differentiable function dy/dx is 0.
What is differentiable function?A differentiable function of one real variable is one that has a derivative at each point in its domain. In other words, a differentiable function's graph has a non-vertical tangent line at each interior point in its domain.
Here,
Given the equation ln x - ln y = y - 4, we can rearrange it to get ln(x/y) = y - 4. Taking the derivative of both sides with respect to x using the chain rule:
d/dx (ln(x/y)) = d/dx (y - 4)
(1/x) (dx/dx) - (1/y) (dy/dx) = dy/dx
dy/dx = (1/y) (dx/dx) + (1/x) (dy/dx) = (1/y) + (1/x) (dy/dx)
Rearranging and solving for dy/dx:
(x/y) (dy/dx) = (1/y) - (1/x)
dy/dx = (x/y^2) (1/x - 1/y) = (x/y^2) (1/x - 1/y)
We can substitute x = 4 and y = 4 into the expression to find the value of dy/dx when x = 4:
dy/dx = (4/16) (1/4 - 1/4) = 0
So, the value of differentiable function dy/dx when x = 4 is 0.
To know more about differentiable function,
https://brainly.com/question/30079101
#SPJ4
What is f(5) if f(1) =3.2 and f(x + 1) = 5/2(f(x))
Answers
Step-by-step explanation:
f(x + 1) = (5/2)*f(x)
f(x + 1) = 2.5*f(x), f(1) = 3.2
f(2) = 2.5f(1) = 2.5*3.2 = 8
f(3) = 2.5f(2) = 2.5*8 = 20
f(4) = 2.5f(3) = 2.5*20 = 50
f(5) = 2.5f(4) = 2.5*50 = 125
In the image, BD bisect ABC. If the measure of ABD is 60, what is the measure of ABC?
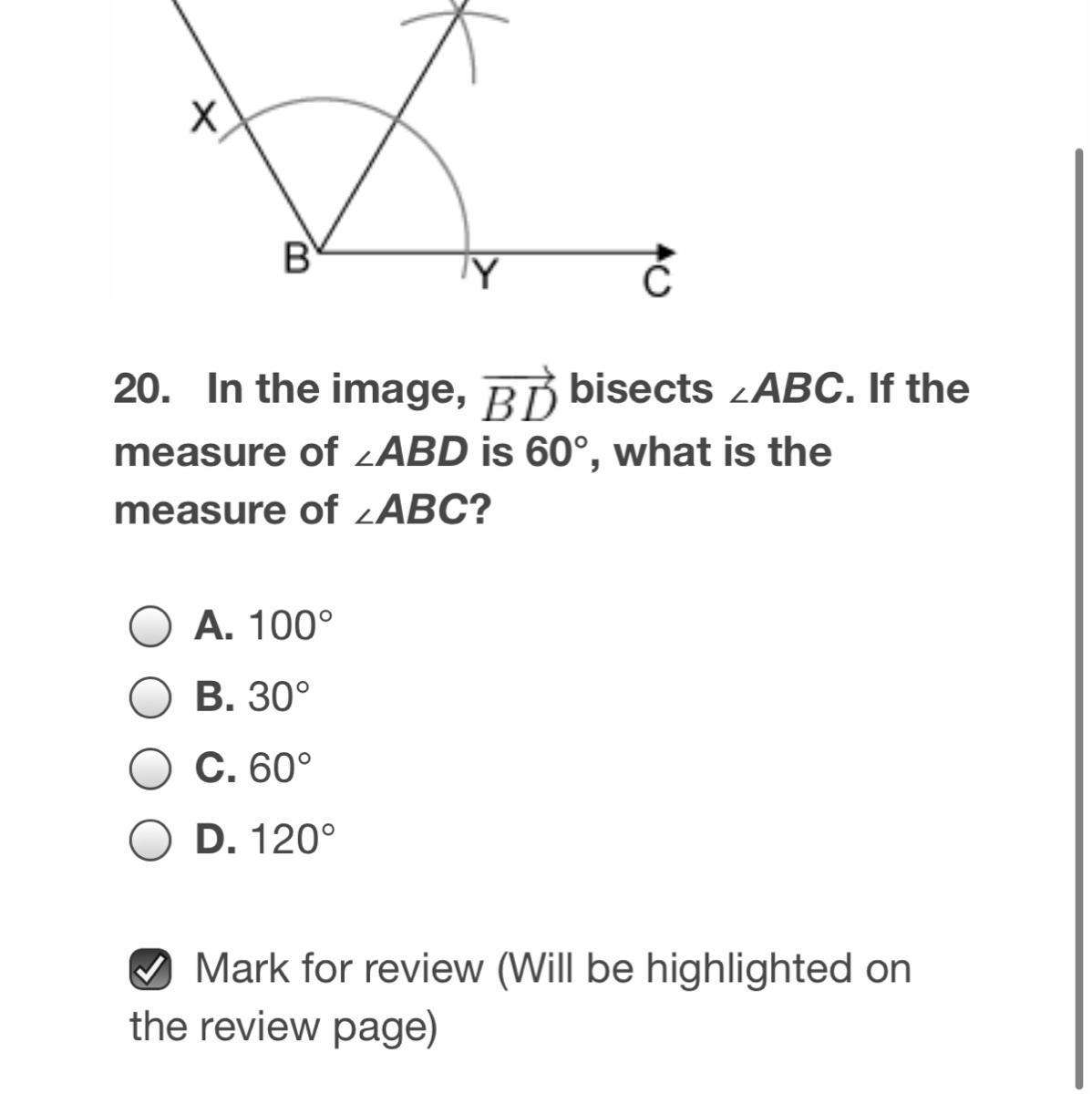
Answers
Answer:
Step-by-step explanation:
60 degree, since bd is bisector so ABC and abd value will be same
plzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz

Answers
Answer:
60 degrees
Step-by-step explanation:
A triangle is 180 degrees and there is already 40 and 80 degrees.
So... 180-80-40=60 degrees.
Hope this helps :D
X+80+40=180
X+120=180
X=180-120
Therefore X=60 degree ans
Hope this helps you!
Please mark it as the brainliest<3
Find the constant of variation for the relation and use it to write an equation for the statement.
If y varies as directly as the square of x, and y
75/8 when x = 5, find y when x = 2
Answers
Answer:
2
Step-by-step explanation:
75/8=5
(75/8)/5=5/5
3 3/4=2
If profits decrease by 13.8% when the degree of operating
leverage (DOL) is 3.8, then the decrease in sales is:
A) 0.28%
B) 0.52%
C) 3.63%
D) 10%
E) 52.44%
Answers
Given that profits decrease by 13.8% when the degree of operating leverage (DOL) is 3.8.
The decrease in sales is: We have to determine the percentage decrease in sales Let the percentage decrease in sales be x.
Degree of Operating Leverage (DOL) = % change in Profit / % change in Sales3.8
= -13.8% / x Thus, we have: x
= -13.8% / 3.8
= -3.63%Therefore, the decrease in sales is 3.63%.Hence, the correct option is C) 3.63%. Percentage decrease in sales = % change in profit / degree of operating leverage
= 13.8 / 3.8
= 3.63% The percentage decrease in sales is 3.63%.
To know more about profits, visit:
https://brainly.com/question/29987711
#SPJ11
Can you help.me with this1/5x=1/4x+2
Answers
Given: An equation:
\(\frac{1}{5}x=\frac{1}{4}x+2\)Solving for x:
\(\begin{gathered} \frac{1}{5}x=\frac{1}{4}x+2 \\ \frac{1}{5}x-\frac{1}{4}x=2 \\ \frac{4x-5x}{20}=2 \\ -x=40 \\ x=-40 \\ \text{Thus, the value of x is 40.} \end{gathered}\)THE FIRST IMAGE OF THE GRAPH IS THE SCATTER PLOT!!!
A scatter plot is shown on the coordinate plane.
scatter plot with points at 1 comma 6, 2 comma 4, 3 comma 2, 3 comma 6, 4 comma 1, 5 comma 4, 6 comma 2, and 9 comma 2
Which of the following graphs shows a line on the scatter plot that fits the data?
scatter plot with points at 1 comma 6, 2 comma 4, 3 comma 2, 3 comma 6, 4 comma 1, 5 comma 4, 6 comma 2, and 9 comma 2, with a line passing through the coordinates 1 comma 6 and 5 comma 4
scatter plot with points at 1 comma 6, 2 comma 4, 3 comma 2, 3 comma 6, 4 comma 1, 5 comma 4, 6 comma 2, and 9 comma 2, with a line passing through the coordinates 3 comma 4 and 7 comma 2
scatter plot with points at 1 comma 6, 2 comma 4, 3 comma 2, 3 comma 6, 4 comma 1, 5 comma 4, 6 comma 2, and 9 comma 2, with a line passing through the coordinates 1 comma 3 and 5 comma 3
scatter plot with points at 1 comma 6, 2 comma 4, 3 comma 2, 3 comma 6, 4 comma 1, 5 comma 4, 6 comma 2, and 9 comma 2, with a line passing through the coordinates 1 comma 6 and 3 comma 2
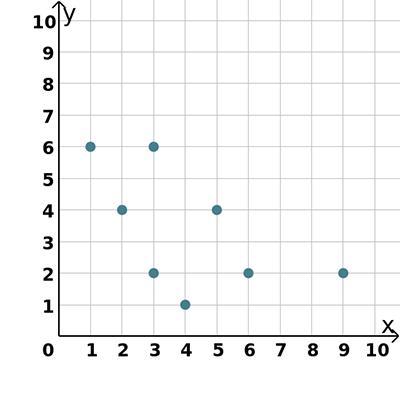




Answers
The correct answer is:
scatter plot with points at (1, 6), (2, 4), (3, 2), (3, 6), (4, 1), (5, 4), (6, 2), and (9, 2), with a line passing through the coordinates (1, 6) and (5, 4).
What is the scatter plot?
A scatterplot shows the relationship between two quantitative variables measured for the same individuals. The values of one variable appear on the horizontal axis, and the values of the other variable appear on the vertical axis. Each individual in the data appears as a point on the graph.
We have given,
scatter plot with points at
(1, 6), (2, 4), (3, 2), (3, 6), (4, 1), (5, 4), (6, 2), and (9, 2),
The first option shows a line passing through the coordinates (1, 6) and (5, 4) which appears to fit the data.
Therefore, the correct answer is:
scatter plot with points at (1, 6), (2, 4), (3, 2), (3, 6), (4, 1), (5, 4), (6, 2), and (9, 2), with a line passing through the coordinates (1, 6) and (5, 4).
To learn more about the scatter plot visit:
https://brainly.com/question/29785223
#SPJ1
Solve 14x -8 > 10x+40
(Multiple choice... options in picture)
DUE IN 5 MINUTES HURRYYYYY

Answers
Answer:
I think its no solution
Step-by-step explanation:
Answer:
x>12
Step-by-step explanation:
i worked it out as quick as possible.. hope this helps :)
what is the probability that 45 or more people in this sample have consumed alcoholic beverages? how does this probability relate to your answer to part (b)?
Answers
The probability that 45 or more people in this sample have consumed alcoholic beverages is 0.0516, or about 5.16 percent.
The probability that 45 or more people in a sample have consumed alcoholic beverages can be determined using normal distribution, as the sample size is sufficiently large. The distribution is also normal because of the large sample size. Using the normal distribution table or a calculator, the probability can be determined. The formula is:
P(X > 44.5) = 1 - P(X ≤ 44.5) = 1 - 0.9484 = 0.0516, approximately.
(Note: We use 44.5 because it is the midpoint of the interval 44.5 to 45.5, which is the one that includes 45.)
Therefore, the probability that 45 or more people in this sample have consumed alcoholic beverages is 0.0516, or about 5.16 percent.
To learn more about probability refer :
https://brainly.com/question/31197941
#SPJ11
simplify.
x⁴y²/x²y*6
Answers
Answer:
x^2y^-4
Step-by-step explanation:
Answer:
i think the answer is x²y/6
find the hcf of 91 , 112 , 49
Answers
Answer: The highest common factor of 91, 112 and 49 is 7
hope this helps :)
Find the slope of the line that contains (-9, 1) and (3,6).
Answers
Answer:
The slope is 5/12
Step-by-step explanation:
To find the slope between any two points, we can use the slope formula:
\(\displaystyle m=\frac{y_2-y_1}{x_2-x_1}\)
Where (x₁, y₁) and (x₂, y₂) are our two points.
We have the two points (-9, 1) and (3, 6).
Let’s let (-9, 1) be (x₁, y₁) and let (3, 6) be (x₂, y₂). Substitute appropriately:
\(\displaystyle m=\frac{6-1}{3-(-9)}\)
Evaluate:
\(\displaystyle m=\frac{5}{12}\)
So, the slope of the line that contains the two points (-9, 1) and (3, 6) is 5/12.
not sure how to do this one! will mark brainliest

Answers
Answer:
\(\frac{1}{6}\)
Step-by-step explanation:
\(-\frac{12}{16} + \frac{11}{12}\)
take lcm of the denominator
lcm=48
\(\frac{-12*3 + 11*4}{48}\)
\(\frac{-36 + 44}{48}\)
\(\frac{8}{48}\)
\(\frac{1}{6}\)
Answer:
\(=\frac{1}{6}\)
Step-by-step explanation:
\(-\frac{12}{16}+\frac{11}{12}\)
the lcm of 16 and 12 is 48
\(-\frac{12}{16} =-\frac{36}{48}\)
\(\frac{11}{12} =\frac{44}{48}\)
\(-\frac{36}{48} +\frac{44}{48}=\frac{8}{48}\)
\(=\frac{1}{6}\)
Hope this helps
To gather information about the elk population, scientists marked 30 elk. Later, they flew over the area and counted 150 elk, 18 of which
were marked.
To the nearest whole number, what is the best estimate of the elk population?
O 198
O 200
O250
O 280
Answers
Answer:
250
Step-by-step explanation:
We can approximate that the scientists counted \(\frac{18}{30}=\frac{3}{5}\) of the elk.
So, the best estimate of the elk population is \(150(5/3)=250\).
Answer:1,250
Step-by-step explanation:
need help please, will give Brainly

Answers
Answer:
evaluate C2 + 4a - b
-2 +4(-5)-3
4=-2-5-3
4=4
=4-4
=0
Draw a Triagle, Square, and Trapezoid.
Answers
Answer:
The triangle, square, and trapezoid are the following:


Consider the differential equation dy/dx = y^2 (2x + 2). Let y = f (x) be the particular solution to the differential equation with initial condition f(0) = -1.(a) find lim\frac{f(x)+1}{sinx}Show the work that leads to your answer.(b) Use Euler's method, starting at x = 0 with two steps of equal size, to approximate f(1/2).(c) find y = f (x), the particular solution to the differential equation with initial condition f(0) = -1
Answers
The limit of (f(x) + 1) / sin(x) as x approaches 0 is 0, the approximation for f(1/2) using Euler's method with two steps is 19/32 and the particular solution to the differential equation with the initial condition f(0) = -1 is: y(x) = -1 / (x² + 2x + 1) - 1.
(a) To find the limit of (f(x) + 1) / sin(x) as x approaches 0, we can first rewrite the given differential equation as:
dy / dx = y² (2x + 2)
Separating variables, we get:
dy / y² = (2x + 2) dx
Integrating both sides, we have:
∫(1 / y² ) dy = ∫(2x + 2) dx
Integrating the left side gives:
-1 / y = x² + 2x + C1
where C1 is the constant of integration.
Since we have the initial condition f(0) = -1, we substitute x = 0 and y = -1 into the above equation:
-1 / (-1) = 0² + 2(0) + C1
1 = C1
So the particular solution is:
-1 / y = x² + 2x + 1
Multiplying through by y gives:
-1 = y(x² + 2x + 1)
Simplifying further:
y(x² + 2x + 1) + 1 = 0
Now, to find the limit (f(x) + 1) / sin(x) as x approaches 0, we substitute x = 0 into the particular solution equation:
f(0)(0² + 2(0) + 1) + 1 = 0
-1(0) + 1 = 0
1 = 0
Therefore, the limit of (f(x) + 1) / sin(x) as x approaches 0 is 0.
(b) Using Euler's method, we approximate the value of f(1/2) starting at x = 0 with two steps of equal size. Let's choose the step size h = 1/4.
First step:
x0 = 0, y0 = f(0) = -1
Using the differential equation, we have:
dy / dx = y² (2x + 2)
dy = y² (2x + 2) dx
Approximating the derivative using the Euler's method:
Δy ≈ y² (2x + 2) Δx
Δy ≈ (-1)² (2(0) + 2) (1/4)
Δy ≈ 1/2
Next, we update the values:
x1 = x0 + Δx = 0 + 1/4 = 1/4
y1 = y0 + Δy = -1 + 1/2 = 1/2
Second step:
x0 = 1/4, y0 = 1/2
Using the differential equation again:
dy / dx = y^2 (2x + 2)
dy = y² (2x + 2) dx
Approximating the derivative using the Euler's method:
Δy ≈ y² (2x + 2) Δx
Δy ≈ (1/2)² (2(1/4) + 2) (1/4)
Δy ≈ 3/32
Updating the values:
x2 = x1 + Δx = 1/4 + 1/4 = 1/2
y2 = y1 + Δy = 1/2 + 3/32 = 19/32
Therefore, the approximation for f(1/2) using Euler's method with two steps is 19/32.
c)To find the particular solution to the differential equation dy/dx = y^2 (2x + 2) with the initial condition f(0) = -1, we can solve the separable differential equation.
Separating variables, we have:
dy / y² = (2x + 2) dx
Integrating both sides:
∫(1 / y² ) dy = ∫(2x + 2) dx
Integrating the left side:
-1 / y = x² + 2x + C
where C is the constant of integration.
To find the particular solution, we substitute the initial condition f(0) = -1:
-1 / (-1) = 0² + 2(0) + C
1 = C
So the particular solution is:
-1 / y = x² + 2x + 1
Multiplying through by y gives:
-1 = y(x² + 2x + 1)
Simplifying further:
y(x² + 2x + 1) + 1 = 0
Therefore, the particular solution to the differential equation with the initial condition f(0) = -1 is: y(x) = -1 / (x² + 2x + 1) - 1
To know more about differential check the below link:
https://brainly.com/question/28099315
#SPJ4
a jar contains 8 blue balls and 4 red balls. if a person selects 6 balls at random, without replacement, what is the probability that all red balls will be selected.
Answers
The probability that all red balls will be selected is 0.0083.
The total number of ways to select 6 balls from the jar is 12C6, which is equal to 495. The number of ways to select only red balls is 4C6, which is equal to 1. So, the probability of selecting all red balls is 1/495 = 0.0083. This means that only a small chance of selecting all red balls exists among all possible selections of 6 balls.
Probability is a mathematical concept that provides a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means an event is impossible and 1 means an event is certain to occur.
Learn more about Probability here:
https://brainly.com/question/7965468
#SPJ4
Ifx=−5andy=2, evaluate the following expressions:i)(4y)2−(2x)2ii)4y2−2x2i)(4y)2−(2x)2=ii)4y2−2x2=
Answers
Answer:
Step-by-step explanation:
-80
Drag the numbers below to put them in order from least to greatest:
8.66 8.6 8.611 8.641 8.63 8.691
Answers
8.6 8.63 8.66 8.611 8.641 8.691
The cost to produce x units of wire is C = 305x +1350 , while the revenue is R = 35x. Find the interval where the product will at least break even.
Answers
The interval where the product will at least break even is \($\left[\begin{array}{cc}\text { Solution: } & x \leq-5 \\ \text { Interval Notation: } & (-\infty,-5]\end{array}\right]$\)
Given C= 305 x+1350C
R=60 x
To find the interval where the product will at least break even we must have \($R(x) \geq c(x)$\)
\($\Rightarrow \quad 35 x \geq 305 x+1350$\)
\($$35 x \geq 305 x+1350$$\)
Subtract 305 x from both sides
\($$35 x-305 x \geq 305 x+1350-305 x$$\)
Simplify
\($$-270 x \geq 1350$$\)
Multiply both sides by - 1 (reverse the inequality)
\($$(-270 x)(-1) \leq 1350(-1)$$\)
Simplify
\($$270 x \leq-1350$$\)
Divide both sides by 270
\(\frac{270 x}{270} \leq \frac{-1350}{270}$$\)
Simplify
\($$x \leq-5$$\)
Mathematical expressions with inequalities are those in which the two sides are not equal. Contrary to equations, we compare two values in inequality. Less than (or less than or equal to), greater than (or greater than or equal to), or not equal to signs are used in place of the equal sign.
To learn more about inequalities visit:https://brainly.com/question/28823603
#SPJ1
Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle. y = x3 − 4x, y = 12x Find the area of the region
Answers
To sketch the region enclosed by the curves y = x^3 - 4x and y = 12x and determine the appropriate method of integration. By evaluating the definite integral ∫[-4 to 4] (12x - (x^3 - 4x)) dx, we can calculate the area of the region enclosed by the given curves.
The curves intersect when x^3 - 4x = 12x. Simplifying this equation, we get x^3 - 16x = 0. Factoring out x, we have x(x^2 - 16) = 0, which gives us x = 0 and x = ±4 as the intersection points.
To determine whether to integrate with respect to x or y, we can observe that the region is vertically bounded by the curves. Therefore, we'll integrate with respect to x.
To find the area of the region, we'll integrate the difference of the upper and lower curves within the given bounds, from x = -4 to x = 4.
Now, for a more detailed explanation:
First, let's analyze the curves individually. The curve y = x^3 - 4x represents a cubic function, and y = 12x represents a linear function. By plotting these curves on a graph, we can observe that they intersect at three points: (0, 0), (-4, -48), and (4, 48).
To determine the enclosed region, we need to find the x-values at which the curves intersect. Setting the two equations equal to each other, we have x^3 - 4x = 12x. Rearranging this equation, we get x^3 - 16x = 0. Factoring out x, we have x(x^2 - 16) = 0, giving us x = 0 and x = ±4 as the x-values of intersection.
Since the region is vertically bounded by the curves, we'll integrate with respect to x. To find the area, we'll integrate the difference between the upper curve (y = 12x) and the lower curve (y = x^3 - 4x) within the bounds from x = -4 to x = 4.
By evaluating the definite integral ∫[-4 to 4] (12x - (x^3 - 4x)) dx, we can calculate the area of the region enclosed by the given curves.
Learn more about enclosed click here: brainly.com/question/32198168
#SPJ11

solve pls brainliest

Answers
Interest = principal x rate x time
Interest = 8000 x 0.03 x 6
Interest = $1,440
Answer: $1,440
Please help meeeeeee

Answers
Answer:
3.5 units
Step-by-step explanation:
Base × Height = Area, so 10 Base × 3.5 Height = 35 units^2
Answer:
3.5 units
Step-by-step explanation:
if the diameter of a circle is 6.4 x 10^8, then the radius of the circle is
Answers
Radius of a circle is the distance from the center of the circle to any point on its circumference. The radius of the circle is 3.2 x 10^8.
The diameter of a circle is twice the length of its radius. So, to find the radius, we divide the diameter by 2.
Given that the diameter is 6.4 x 10^8, we divide it by 2 to get the radius: (6.4 x 10^8) / 2 = 3.2 x 10^8.
To calculate the radius of a circle, you need to know either the diameter or the circumference. If you have the diameter (the distance across the circle passing through the center), you can divide it by 2 to find the radius. If you have the circumference (the distance around the circle), you can use the formula: radius = circumference / (2 * π), where π is a mathematical constant approximately equal to 3.14159.
The radius of the circle is 3.2 x 10^8.
To know more about radius follow the link:
https://brainly.com/question/27696929
#SPJ11
Solve 5/6= 4/x
A. 7
B. 4.6
C. 5
D.4.8
Answers
Answer:
I think it's D, i might be wrong but im pretty sure it's D
What is the approximate volume of the cone?
Use 3.14 for π.
A 1206 cm³
B 2170 cm³
C 3260 cm³
C 6510 cm³

Answers
Answer:
A. 1206 cm³
Step-by-step explanation:
We have a cone and are asked to find the approximate volume of it.
Keep in mind we are using π for 3.14
The forumla of a cone is V = πr²\(\frac{h}{3}\)
We know the radius = 12
and the height = 8
Substitute :
V = π12²\(\frac{8}{3}\)
Since these are multiplied with each other, we can first start off with multiplying the fraction, including with factoring 12²:
V = \(\frac{2^4*3^2*8\pi }{3}\)
Cancel the common factor - 3 :
V = \(2^4 * 8 * 3\pi\)
Multiply 8 and 3π :
V = \(2^4 * 24\pi\)
Solve the exponent :
V = \(16 * 24\pi\)
Multiply :
V = \(384\pi\)
Multiply for the final answer :
1205.76 cm³
which can be rounded up to
A. 1206 cm³