Eva earns $5.50 per hour and time-and-a-half for overtime for all hours over 40 hours. How much did she earn the week she worked 47 hours?
Answers
Answer:
$277.75
5.50×40=220
5.50÷2=2.75
5.50+2.75=8.25×7=57.75
57.75+220=277.75
Related Questions
what is the final step in creating a frequency distribution? multiple choice question. set individual class limits. count the number of observations in each class. determine class width. decide on the number of classes.
Answers
The final step in creating a frequency distribution is to count the number of observations in each class. After determining the class width and deciding on the number of classes, the next step is to set individual class limits.
This involves establishing the lower and upper limits for each class interval. Once the class limits have been set, the next step is to tally the number of observations that fall within each interval. This process involves counting the number of data points that fall within each class and recording this information in a tally chart. After tallying the number of observations in each class, the final step is to create a frequency table that summarizes this information. The frequency table will typically include the class intervals, the frequency (i.e., the number of observations) in each interval, and the relative frequency (i.e., the proportion of observations) in each interval. By following these steps, you can create a comprehensive frequency distribution that provides insights into the distribution of your data.
To learn more about frequency distribution : brainly.com/question/28406412
#SPJ11
what is the y-int of the curve

Answers
Answer:
The y-intercept is (0,3)
Step-by-step explanation:
What is the value of x?

Answers
Answer:
As x is the exterior angle
Step-by-step explanation:
therefore
let name the angle exterior angle be ACE
interior angleABC=76°and angleBAC=55°
sum of 2 interior angle is equal to exterior angle
=76+55=x
=131=x
brian rehr obtains an installment loan of 1250 to buy canoe requires 24 monthly payments and has an apr of 10%
What is the monthly payment and finance charge
Answers
Answer:
I believe it is 122.6
Step-by-step explanation:
1,250 - 24 = 1,226
10%of 1,226 = 122.6
What are the possible vaules of x it (4x-5)2=49?
Answers
\(\boxed{The\:value\:of\:x\:is\:7.375.}\)
\(\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\orange{:}}}}}\)
\((4x - 5)2 = 49 \\ ⇢8x - 10 = 49 \\⇢8x = 49 + 10 \\ ⇢8x = 59 \\ ⇢x = \frac{59}{8} \\ ⇢x = 7.375\)
Therefore, the value of x is 7.375.
\({ \bf{ \underbrace{To\:verify :}}}\)
\((4x - 5)2 = 49 \\ ⇢(4 \times 7.375 - 5)2 = 49 \\ ⇢(29 .5 - 5)2 = 49 \\ ⇢24.5 \times 2 = 49 \\ ⇢49 = 49 \\ ⇢ L.H.S.=R. H. S\)
Hence verifed.
\(\large\mathfrak{{\pmb{\underline{\orange{Happy\:learning }}{\orange{.}}}}}\)
the chance of rain on a given day in seattle is 70%. if it rains, the chance that a food truck will incur a loss on that day is 80%. if it does not rain, then the chance of loss is 10%. on a randomly chosen day if the food truck has not incurred a loss, what is the probability that it had not rained that day?
Answers
The probability of incurring a loss when it rains is:P (loss | raining) = 80%So, there is a 20% chance that the food truck will not have incurred a loss when it rains.
The P (not raining | not loss) = 90% × 30% = 27%.Thus, the probability that it had not rained on that randomly selected day given that the food truck did not incur a loss is 27%.
The chance of not raining on a given day in Seattle can be calculated as follows:When it does not rain, there is a 10% probability that the food truck will incur a loss, as given in the statement. Similarly, when it rains, there is an 80% chance that the food truck will incur a loss on that day.
To calculate the probability that the food truck will not have incurred a loss on that day, we must first calculate the probability that the food truck will have incurred a loss on that day.Suppose the probability of rain is 70%, so the chance that it won't rain will be: P (not raining) = 100% - 70% = 30%When it rains, there is a 80% probability that the food truck will have incurred a loss, as given in the statement.
The probability of not incurring a loss when it does not rain is:P (not loss | not raining) = 100% - 10% = 90%The probability of not raining when the food truck does not incur a loss can be calculated as follows:P (not raining | not loss) = P (not loss | not raining) × P (not raining)P (not loss | not raining) = 90%P (not raining) = 30%
Learn more about Probability
brainly.com/question/11234923
#SPJ11
beginning with s2, the ball takes the same amount of time to bounce up as it does to fall, and so the total time elapsed before it comes to rest is given by t = 1 2 [infinity] (0.8)n. n = 1
Answers
With n = 1, the total time elapsed before the ball comes to rest is 0.4 units of time. The total time elapsed before the ball comes to rest is represented by the formula t = (1/2)∑(0.8)^n as n approaches infinity.
The ball takes the same amount of time to bounce up as it does to fall, starting from the second bounce (n = 1). This means that for each subsequent bounce, the time it takes for the ball to reach its maximum height and return to the ground is the same.
The total time elapsed before the ball comes to rest is given by the formula t = (1/2)∑(0.8)^n, where n represents the number of bounces and ∑ denotes the summation notation. In this case, the summation starts from n = 1 and goes to infinity.
To calculate the total time, we substitute n = 1 into the formula: t = (1/2)(0.8)^1 = 0.4. Therefore, with n = 1, the total time elapsed before the ball comes to rest is 0.4 units of time.
to practice more on time elapsed problems, visit: brainly.com/question/30266030
#SPJ11
What points are \(\sqrt{45}\) units away from (-3, 1)? Select all that apply.
1. (0,7)
2. (-9,4)
3. (3,-2)
3. (-6,-5)
Answers
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I, find the value of tan(A−B).
Answers
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I. The value of tan(A-B) is -23/33.
What is the value of tan(A-B)?We can start by using the identity: tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
From the given information, we have:
cos A = 24/25, which means sin A = sqrt(1 - cos^2 A) = 7/25 (since A is in Quadrant I)
tan B = 4/3, which means sin B = 4/sqrt(4^2 + 3^2) = 4/5 and cos B = 3/sqrt(4^2 + 3^2) = 3/5
Now, we can use the definitions of sine and cosine to find tan A:
tan A = sin A / cos A = (7/25)/(24/25) = 7/24
Substituting the values we have found into the formula for tan(A - B), we get:
tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
= [(7/24) - (4/3)]/[1 + (7/24)(4/3)]
= (-13/72)/(25/72)
= -13/25
Therefore, tan(A - B) = -13/25.
Learn more about tan(A - B) here:https://brainly.com/question/24305408
#SPJ1
Need help finding this angle
will mark as brainliest
do not attach a file or i will report you
thanks!

Answers
Step-by-step explanation:
Here's my step by step solution Friend..

The width of a rectangle is 2 cm less than the length. The
perimeter is greater than 28 inches. Describe the dimensions
of the rectangle.
Length=?
Width=?
Answers
Answer:
2+2+28+28=60 is the answer of the perimeter
Step-by-step explanation:
Inequalities help us to compare two unequal expressions. The length of the rectangle can be 19 cm, while its width will be 17 cm.
What are inequalities?Inequalities help us to compare two unequal expressions. Also, it helps us to compare the non-equal expressions so that an equation can be formed.
It is mostly denoted by the symbol <, >, ≤, and ≥.
Let the length of the rectangle be represented by x centimeters. Given the width of a rectangle is 2 cm less than the length. Therefore, the width of the rectangle is (x-2) centimeters.
Since the perimeter of the rectangle should be greater than 28 inches, therefore,
Perimeter of the rectangle > 28 inches × 2.54 = 71.12 centimeters
Now, given the perimeter is greater than 28 inches. Therefore,
2[x+(x-2)] > 71.12
x + (x-2) > 35.56
x + x - 2 > 35.56
2x - 2 > 35.56
2x > 37.56
x > 18.78
x = 19
Thus, the length of the rectangle can be 19 cm, while its width will be 17 cms.
Learn more about Inequality:
https://brainly.com/question/19491153
#SPJ1
please answer as soon as possibly
the mass of the rock Gibraltar is 1.78 x 10^12 kilograms 10^12 kilogram. The mass of the antarctic iceberg is 4.55 x 10^13 kilograms. approximately how many more kilograms is the mass of the antarctic iceberg than the mass of the Rock of Gibraltar? show your work and write your answer is scientific notation.
Answers
Answer:
2.56×101 hope this helps!:)
Step-by-step explanation:
4.55×1013
_________≈2.56×101
1.78∗1012
In a circle, what is the ratio of the circumference to its diameter?
A area
B radius
C volume
D Pi
Answers
Answer:
the answer is D
Step-by-step explanation:
whats the value of x in the triangle 9 3
Answers
Answer:
X = 9.4868
Step-by-step explanation:
Use the pythagorean theorem
a squared plus b squared equals c squared
in this case c equals x
A&b are the side and base length of a right triangle
Find d²y/dx² in terms of x and y.
y^5 = x^7
d²y/dx² =????
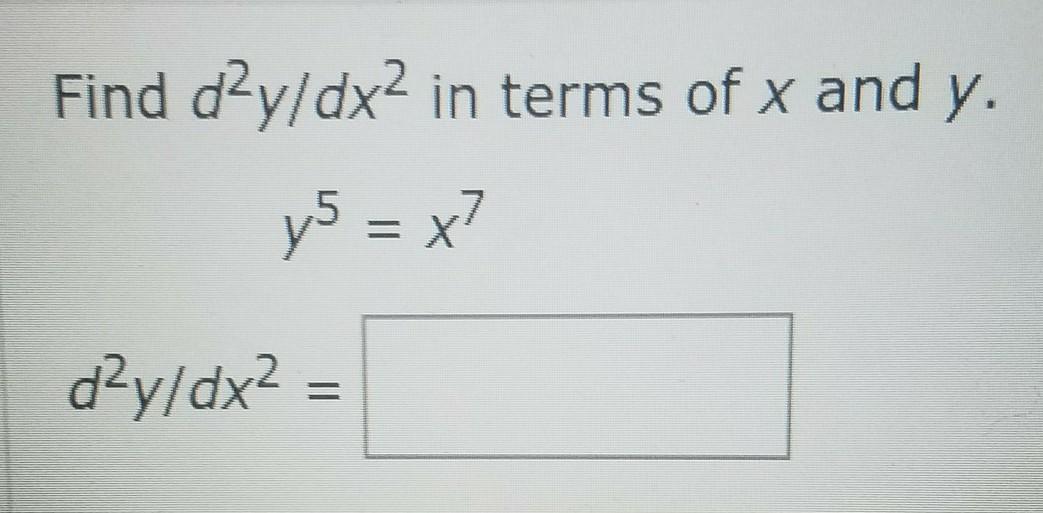
Answers
Answer: \(\frac{14y}{25x^2}\)
====================================================
Work Shown:
First calculate \(\frac{dy}{dx}\) through the use of implicit differentiation.
Don't forget about the chain rule.
\(y^5 = x^7\\\\\frac{d}{dx}\left[y^5\right] = \frac{d}{dx}\left[x^7\right]\\\\5y^4\frac{dy}{dx} = 7x^6\\\\\frac{dy}{dx} = \frac{7x^6}{5y^4}\\\\\)
Go back to line 3, shown above, and apply the derivative to both sides.
You'll be using the product rule.
\(5y^4\frac{dy}{dx} = 7x^6\\\\\frac{d}{dx}\left[5y^4\frac{dy}{dx}\right] = \frac{d}{dx}\left[7x^6\right]\\\\\frac{d}{dx}\left[5y^4\right]*\frac{dy}{dx}+5y^4*\frac{d}{dx}\left[\frac{dy}{dx}\right] = 42x^5\\\\20y^3*\frac{dy}{dx}*\frac{dy}{dx}+5y^4*\frac{d^2y}{dx^2}=42x^5\\\\20y^3*\left(\frac{dy}{dx}\right)^2+5y^4*\frac{d^2y}{dx^2} = 42x^5\\\\\)
Use substitution and isolate \(\frac{d^2y}{dx^2}\) to get the following:
\(20y^3*\left(\frac{dy}{dx}\right)^2+5y^4*\frac{d^2y}{dx^2} = 42x^5\\\\20y^3*\left(\frac{7x^6}{5y^4}\right)^2+5y^4*\frac{d^2y}{dx^2} = 42x^5\\\\\frac{196x^{12}}{5y^5}+5y^4*\frac{d^2y}{dx^2} = 42x^5\\\\\frac{196x^{12}}{5x^7}+5y^4\frac{d^2y}{dx^2} = 42x^5\\\\\)
\(\frac{196x^5}{5}+5y^4*\frac{d^2y}{dx^2}=42x^5\\\\5y^4*\frac{d^2y}{dx^2}=42x^5-\frac{196x^5}{5}\\\\5y^4*\frac{d^2y}{dx^2}=\frac{210x^5-196x^5}{5}\\\\5y^4*\frac{d^2y}{dx^2}=\frac{14x^5}{5}\\\\\)
\(\frac{d^2y}{dx^2}=\frac{14x^5}{5}*\frac{1}{5y^4}\\\\\frac{d^2y}{dx^2}=\frac{14x^5}{25y^4}\\\\\frac{d^2y}{dx^2}=\frac{14x^5*x^2}{25y^4*x^2}\\\\\frac{d^2y}{dx^2}=\frac{14x^7}{25y^4*x^2}\\\\\frac{d^2y}{dx^2}=\frac{14y^5}{25y^4*x^2}\\\\\frac{d^2y}{dx^2}=\frac{14y}{25x^2}\\\\\)
x=5/2; f(x) = (12/15)x -200 =

Answers
Answer:
The answer would be the letter c
A local little league has a total of 80 players, of whom 40% are right handed. how many right handed players are there?
Answers
Answer:
32
Step-by-step explanation:
A submarine is situated 400 feet below sea level. If it drops another 250 feet below sea level, what is the new position?
Answers
Answer:
-650ft
Step-by-step explanation:
I took a test with a question like that
After drinking, the body eliminates 37% of the alcohol present in the body per hour.
a) The amount of alcohol in grams in the body on an hourly basis is described by a discrete time dynamical system (DTDS) of the form xn+1=f(xn), where xn is the number of grams of alcohol in the body after n hours. Give the updating function f (as a function of the variable x).
b) Peter had three alcoholic drinks that brought the alcohol content in his body to 41 grams, and then he stopped drinking. Give the initial condition (in grams) for the DTDS in (a).
c) Find the solution of the DTDS in (a) with the initial condition given in (b). (Your answer will be a function of the variable n, which represents time in hours.)
Answers
The solution of the DTDS is xn = (0.63)^n * 41 grams, where n represents time in hours.
a) The updating function f(x) for the discrete time dynamical system (DTDS) can be derived from the given information that the body eliminates 37% of the alcohol present in the body per hour.
Since 37% of the alcohol is eliminated, the amount remaining after one hour can be calculated by subtracting 37% of the current amount from the current amount. This can be expressed as:
f(x) = x - 0.37x
Simplifying the equation:
f(x) = 0.63x
b) The initial condition for the DTDS is given as Peter having 41 grams of alcohol in his body after consuming three alcoholic drinks. Therefore, the initial condition is:
x0 = 41 grams
c) To find the solution of the DTDS with the given initial condition, we can use the updating function f(x) and iterate it over time.
For n hours, the solution is given by:
xn = f^n(x0)
Applying the updating function f(x) repeatedly for n times:
xn = f(f(f(...f(x0))))
In this case, since the function f(x) is f(x) = 0.63x, the solution can be written as:
xn = (0.63)^n * x0
Substituting the initial condition x0 = 41 grams, the solution becomes:
xn = (0.63)^n * 41 grams
Learn more about function at: brainly.com/question/30721594
#SPJ11
A machine that is used to regulate the amount of dye dispensed for mixing shades of paint can be set so that it discharges μ milliliters of dye per can of paint. The amount of dye discharged is known to have a normal distribution with mean μ (the amount the user specifies), and a standard deviation of 0.6 milliliters. If more than 8 milliliters of dye are discharged when making a certain shade of blue paint, the shade is unacceptable. Determine the setting for μ so that only 5% of the cans of paint will be unacceptable.
Answers
The machine should be set at approximately 7.006 milliliters of dye per can of paint.
How to determine the setting for μ?To determine the setting for μ so that only 5% of the cans of paint will be unacceptable, follow these steps:
1. Recognize that the amount of dye discharged follows a normal distribution with mean μ and a standard deviation of 0.6 milliliters.
2. Define unacceptable as discharging more than 8 milliliters of dye per can.
3. Use the z-score formula to find the z-value corresponding to 5% probability in the right tail (unacceptable region) of the distribution. Since we want only 5% of the cans to be unacceptable, we'll look for the z-value that corresponds to the 95th percentile (1 - 0.05 = 0.95).
4. Consult a standard normal table or use an online calculator to find the z-value corresponding to a cumulative probability of 0.95. The z-value is approximately 1.645.
5. Use the z-score formula to solve for μ:
z = (X - μ) / standard deviation
1.645 = (8 - μ) / 0.6
6. Solve for μ:
8 - μ = 1.645 * 0.6
μ = 8 - (1.645 * 0.6)
μ ≈ 7.006
Your answer: The machine should be set at approximately 7.006 milliliters of dye per can of paint to ensure that only 5% of the cans will be unacceptable.
Learn more about population mean
brainly.com/question/30727743
#SPJ11
Determine the period.
Enter

Answers
Answer:
Your answer should be \(\frac{\pi }{7}\)
Step-by-step explanation:
Looking at the x-axis we can say that is our b.
Period Formula: 2π/b.
x-axis is from 0 to 20.
b = 14 because of the rise to rise.
2π/14 = π/7
Helen has a garden in the shape of a circle of diameter 20 m.
She is going to cover all the garden with grass seed to make a lawn.
Grass seed is sold in boxes.
Each box of grass seed will cover 58 m² of garden.
a) Taking it to be 3.14 work out the area of the garden in m? (2)
20 m
b) Work out an estimate for the number of boxes of grass seed Helen needs.
To find your estimate, round each of the numbers in your working
to 1 significant figure. You must show your working. (2)
c) Your estimate for b) is
(1)
A an overestimate B an underestimate C could be either.
Total marks: 5
Answers
a. The area of the garden is 314m².
b. The number of boxes of grass Helen needs is 5 boxes.
c. My estimate for b is an underestimate.
A circle is a bounded object with points from its center to its circumference is equidistant.
Area of a circle = πr²
Where :
π = pi = 3.14
R = radius = diameter / 2 = 20m / 2 = 10m
3.14 x 10² = 314m²
Number of boxes needed to cover the garden = area of the garden / coverage of one box
314m² / 58m² = 5.14
5 boxes to one significant figure.
To learn more about the area of a circle, please check: https://brainly.com/question/21979774?referrer=searchResults

a. The area of the garden is 314m².
b. The number of boxes of grass Helen needs is 5 boxes.
c. My estimate for b is an underestimate.
A circle is a bounded object with points from its center to its circumference that is circumferenced equidistant.
Area of a circle = πr²
Where : π = pi = 3.14
R = radius = diameter / 2 = 20m / 2 = 10m
3.14 x 10² = 314m²
Number of boxes needed to cover the garden = area of the garden / coverage of one box
314314m² / 58m² = 5.14
5 boxes to one significant figure.
21. A triangle has vertices A(-2,4), B(6,2), and C(1,-1). Prove using the Distance Formula and
Slope Formula that ABC is an isosceles right triangle.
Answers
To prove that triangle ABC is an isosceles right triangle, we need to show that two sides of the triangle are equal in length and one angle is a right angle.
Distance Formula:
The distance between two points (x₁, y₁) and (x₂, y₂) is given by the distance formula:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Using the distance formula, we can calculate the lengths of the three sides of the triangle:
Side AB: d₁ = √[(6 - (-2))² + (2 - 4)²] = √[8² + (-2)²] = √(64 + 4) = √68
Side BC: d₂ = √[(1 - 6)² + (-1 - 2)²] = √[(-5)² + (-3)²] = √(25 + 9) = √34
Side AC: d₃ = √[(-2 - 1)² + (4 - (-1))²] = √[(-3)² + 5²] = √(9 + 25) = √34
Slope Formula:
The slope between two points (x₁, y₁) and (x₂, y₂) is given by the slope formula: m = (y₂ - y₁) / (x₂ - x₁)
Using the slope formula, we can calculate the slopes of the three sides of the triangle:
Slope AB:
m₁ = (2 - 4) / (6 - (-2)) = (-2) / 8 = -1/4
Slope BC:
m₂ = (-1 - 2) / (1 - 6) = (-3) / (-5) = 3/5
Slope AC:
m₃ = (4 - (-1)) / (-2 - 1) = 5 / (-3) = -5/3
From the distances calculated and the slopes of the sides, we can see that side AB is equal in length to side BC (both √34), indicating that two sides are equal. Additionally, the slope of side AC (m₃ = -5/3) is the negative reciprocal of the slope of side AB (m₁ = -1/4), indicating that the two sides are perpendicular, and hence, one angle is a right angle.
Therefore, triangle ABC is an isosceles right triangle.
Learn more about isosceles here
https://brainly.com/question/29793403
#SPJ11
The selling price of an article is 20% less than its marked price and the marked
price is 30% above the cost price. Find the profit percent.
Answers
Answer:
sp=mp-20%ofmp=0.8mp
mp=cp+30%ofcp=1.3cp
mp=1.3cp
cp=mp/1.3
profit %=?
Step-by-step explanation:
profit=sp-cp=0.8mp-mp/1.3=(1.04mp-mp)/1.3=0.04mp/1.3=0.0307mpProfit %=profit/cp×100%=0.0307mp/mp/1.3×100%=0.0307×1.3×100%=3.991%=4%The profit percentage is 4% .
What is profit percentage?Profit percentage (%) is the amount of profit expressed in terms of percentage. This profit is based on the cost price .
Formula for profit percentage is:
(Profit/Cost Price) × 100
where,
Profit = Selling price - Cost price
According to the question
Let Cost price of the article = 100x
marked price is 30% above the cost price
i.e marked price = \(\frac{130}{100} * 100x\)
= 130 x
selling price of an article is 20% less than its marked price
i.e Selling price of the article = \(130x * \frac{100-20}{100}\)
= \(130x * \frac{80}{100}\)
= 104 x
Now ,
Profit = Selling price - Cost Price
Profit = 104x -100x
Profit = 4x
Profit percentage = \(\frac{Profit}{Cost PRice} *100\)
substituting the values in formula
Profit percentage = \(\frac{4x}{100x} *100\)
Profit percentage = 4%
Hence, the profit percentage is 4% .
To know more about profit percentage here:
https://brainly.com/question/11018349
#SPJ2
A retail shop is replacing their flooring with laminate wood. The floor plan is shown below. Determine the total square feet of laminate wood needed to complete the job.

Answers
===========================================================
Explanation:
As shown in the diagram below, I've drawn a blue horizontal line to split the figure into two rectangles (smaller one up top, larger down below).
The smaller rectangle up top is 25 ft by 8 ft, giving an area of 25*8 = 200 sq ft.
The larger rectangle down below is 35 ft by 25 ft so we have an area of 35*25 = 875 sq ft.
The total area is 200+875 = 1075 square feet
Notes:
We can write "square feet" as "sq ft" or as "ft^2" without quotes.The portion "5 ft", in the upper left corner, is never used.
a and b are vectors that are not parallel
:)

Answers
The parallel vectors to CD are:
V = 20a - 15bV' =10a - 20b + 2a + 11bV'' = (-8a + 6b) = -2*(4a - 3b) V''' = a - (3/4)b = (1/4)*(4a - 3b)Which vectors are parallel to CD?Here we have the vector:
CD = 4a - 3b
Where a and b are vectors.
A vector V will be parallel to CD if we can find a scalar number k such that we can write the vector as:
V = k*CD
The second option:
V = 20a - 15b
We can rewrite this as:
V = 20a - 15b = 5*(4a - 3b) this vector is parallel.
The third one is:
V' =10a - 20b + 2a + 11b
V' = 12a - 9b = 3*(4a - 3b) this vector is parallel.
V'' = (-8a + 6b) = -2*(4a - 3b) this vector is parallel.
V''' = a - (3/4)b = (1/4)*(4a - 3b) this vector is parallel.
These are all the parallel vectors.
Learn more about vectors at:
https://brainly.com/question/3184914
#SPJ1
There are 20 black, 15 white, 12 green, 12 red, 9 blue, and 2 yellow candies in a box. How many candies should you take (without looking at them) to be sure that you have at least 3 candies the same color?
Answers
Answer:
All of them lol.
Step-by-step explanation:
If you take all of them, you have a 100% chance at getting at LEAST 3 candies of the same color.
Create a function called sensor_value that randomly generates a number between ( 0 and 3 ). Create a new function called Gate_Control that uses the function sensor_value to generate two semaphores: Gate and Counter. The semaphore Gate is passed if the output is 2 . On the other hand the semaphore Counter is passed if the output is 1 , or 3 ). Then create a thread using the Gate_Control function. C should be used and code should be ready to be executed
Answers
We have been able to create a thread that uses Gate_Control function and then shown the code generated.
How to use the Gate Control Function?A thread that uses Gate_Control function and the code generated is as follows:
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#include <semaphore.h>
#include <unistd.h>
sem_t Gate, Counter;
// Function to generate a random number between 0 and 3
int sensor_value() {
return rand() % 4;
}
// Function for the Gate_Control thread
void* Gate_Control(void* arg) {
while (1) {
int value = sensor_value();
if (value == 2) {
// Passing the Gate semaphore
sem_post(&Gate);
}
if (value == 1 || value == 3) {
// Passing the Counter semaphore
sem_post(&Counter);
}
usleep(1000000); // Wait for 1 second
}
return NULL;
}
int main() {
srand(time(NULL));
// Initialize semaphores
sem_init(&Gate, 0, 0);
sem_init(&Counter, 0, 0);
// Create the Gate_Control thread
pthread_t gateControlThread;
pthread_create(&gateControlThread, NULL, Gate_Control, NULL);
// Main thread waits for the Gate semaphore
while (1) {
sem_wait(&Gate);
// Gate semaphore passed
printf("Gate semaphore passed\n");
}
// Cleanup and exit
sem_destroy(&Gate);
sem_destroy(&Counter);
return 0;
}
Read more about Gate control Function at: https://brainly.com/question/30825273
#SPJ1
"When dividing powers of the same base, such as x^3/x^5, you will _____________ the exponents
Answers
the rule for division is:
\(\frac{x^a}{x^b}=x^{a-b}\)Then:
you will substract the exponents
Which circle will have the largest circumference?
O OA,r= 3 cm
O OB,r= 2 cm
OC,r= 6 cm
OD, r= 5 cm