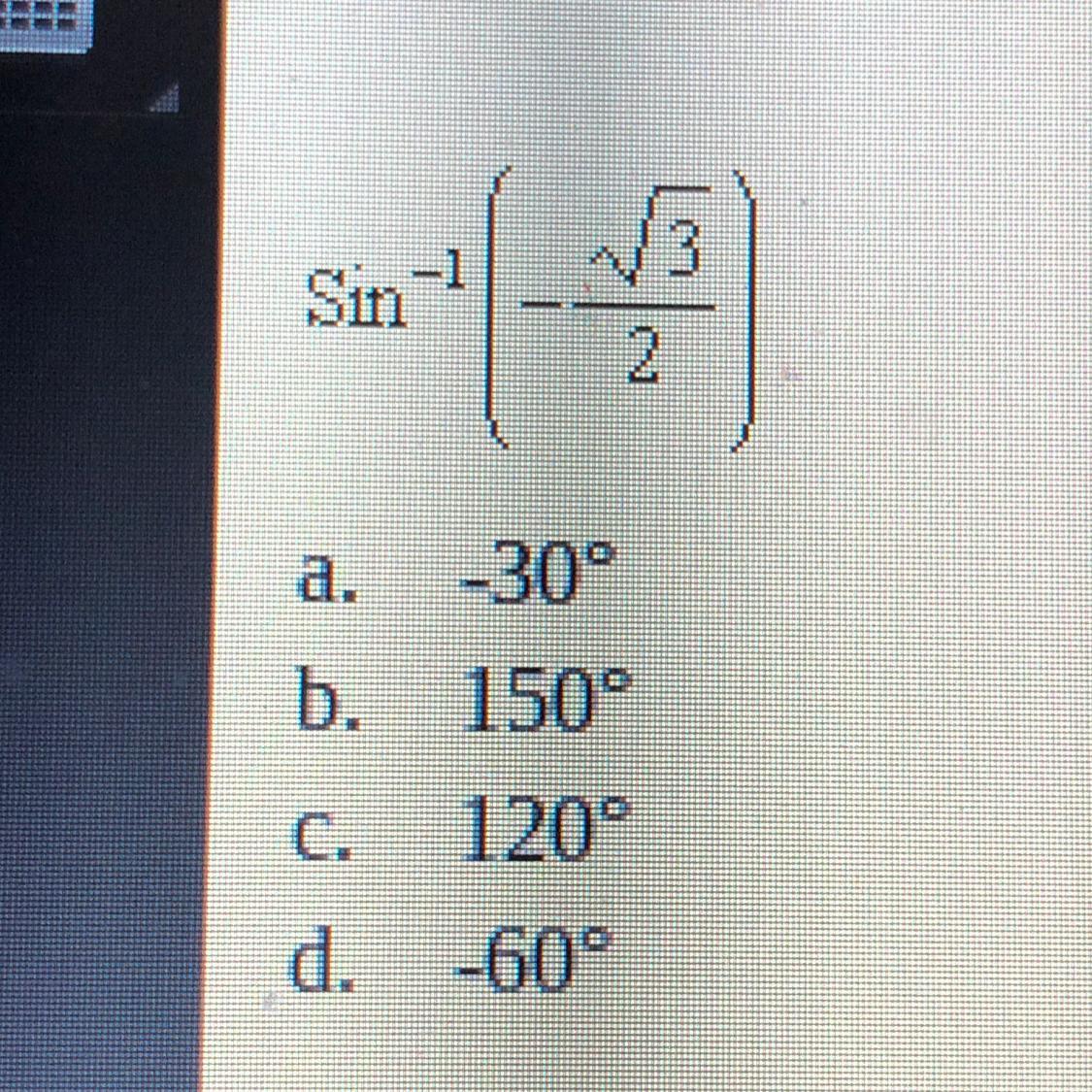Answers
Answer:
-60
hope it helps
Related Questions
1 foot = 0.305 meters to convert 20 meters into feet.
20 meters = feet
Answers
20 meters equal to 65.6168 feet by unit conversion.
What is unit conversion?
The process of translating measurements of a given quantity between different units, frequently using mathematical conversion factors that change the measurement of the quantity without changing its effects, is known as unit conversion.The specific circumstances or the desired result dictate the conversion process. This may be governed by regulation, contract, set of technical requirements, or other publicly available standards.Certain measurements must be accurately converted from one system to another without compromising the accuracy of both the original measurement.Each conversion factor is chosen based on the relationship here between particular pair of original units and a particular pair of target units.Using the given information about unit conversion, that,
1 foot = 0.305 meters
1 meter= (1/0.305) feet
20 meters = (1/0.305)*20 = 65.6168 feet
Learn more about unit conversion here: https://brainly.com/question/13016491
#SPJ9
What are the partial products that result from multiplying 15 x 32? (____ x ____) + (____ x ___) + (____ x ____) + (____ x ____)
Answers
Dividing both into this (15 x 32) below.
15=10+5
32=30+2 and both of the equations will give you the result of 4 partial products.
10x30=300
5x30=150
10x2=20
5x2=10
Solve *please show work* :)

Answers
Answer:
E.200.5ft²
Step-by-step explanation:
To find the area of the composite figure we simply split it into two regular shapes, a half circle and a square, we then find the area of the two shapes individually and add them together.
Area of square = s² where s = side length
It appears the given side length is 12 so s = 12
Which means area = 12² = 144ft²
For semi circle
Area = 1/2(πr² ), where r is the radius
The side length of the square is shared with the diameter of the semi circle meaning that the diameter of the semi circle is 12
To convert to radius from diameter we simply divide by 2 so r = 12/2 = 6
We have area = 1/2(πr² ) and r = 6
So area = 1/2(π6²)
==> evaluate exponent
Area = 1/2(36π)
==> take one half of 36
Area = 18π
==> multiply 18 and π
Area = about 56.5
Finally we add the two areas together
Total area = 56.5 + 144 = 200.5ft²
Describe and correct the error in listing the coordinates of the image after a dilation with a scale factor of 1/2.

Answers
Each coordinate was multiplied by 2 instead of divided by 2
the correct coordinates are
preimage image
A (2, 5) → (2 * 1/2, 5 * 1/2) → A' (1, 2.5)
B (2, 0) → (2 * 1/2, 0 * 1/2) → B' (1, 0)
C (4, 0) → (4 * 1/2, 0 * 1/2) → C' (2, 0)
How to find the coordinates of the imageDilation is a method of transformation that magnify or shrink the preimage depending on the scale factor
The transformation rule for dilation is as follows
(x, y) for a scale factor of r → (rx, ry)
following similar procedure for the given problem we solve with scale factor of 1/2
preimage image
A (2, 5) → (2 * 1/2, 5 * 1/2) → A' (1, 2.5)
B (2, 0) → (2 * 1/2, 0 * 1/2) → B' (1, 0)
C (4, 0) → (4 * 1/2, 0 * 1/2) → C' (2, 0)
Learn more about transformation here:
https://brainly.com/question/29329662
#SPJ1
a theater has (2x+1) rows of seats, with (x-3) seats in each row. how many seats are in the theater?
A. 2x^2- 5x- 3
B. 2x^2+ 5x- 3
C. 2x^2- 7x+ 3
D. 2x^2- 7x- 3
Answers
(2x+1)(x-3)
y(x-3) .... let y = 2x+1
y*x+y(-3) .... distribute
xy - 3y
x( y ) - 3( y )
x( 2x+1 ) - 3( 2x+1) ... replace y with 2x+1
2x^2 + x - 6x - 3 ..... distribute
2x^2 - 5x - 3
Answer is choice A
Need help urgently difficult but simple math equation if you get it right ill give you brainliest.

Answers
Answer:
No.
Step-by-step explanation:
Explanation below.

At your child's birth, you begin contributing monthly to a college fund. The fund pays an APR of 4.1% compounded monthly. You figure your child will need $40,000 at age 18 to begin college. What monthly deposit is required? (Round your answer to the nearest cent.)
Answers
Answer:
$185.19
Step-by-step explanation:
Completing the square x^2+16x+63=0
Answers
The square of x² + 16x + 63 = 0 is given by (x + 8)² = 127.
Given that,
x² + 16x + 63 = 0
To complete the square of above given equation.
Power is the degree of values that are mentioned at the superscript of the value.
Here,
x² + 16x + 63 = 0
Dividing the coefficient of x by 2, and adding and subtracting the square of the quotient.
x² + 16x + 64 - 64 - 63 = 0
(x + 8)² = 127
Thus, the square of x² + 16x + 63 = 0 is given by (x + 8)² = 127.
Learn more about powers here:
https://brainly.com/question/27809901
#SPJ1
Let V be the space of all infinite sequences of real num- bers. See Example 5. Which of the subsets of V given in Exercises 12 through 15 are subspaces of V? 12. The arithmetic sequences [i.e. sequences of the form (a,a + k;a + 2k,u 3k for some constants CL and k]
Answers
Yes , the arithmetic sequence ( written as sequences of the form (a , a+k , a+2k , a+3k for some constants a and k ) is a subspace of V .
To determine whether subsets of V in the arithmetic sequences are subspaces of V, we check if they satisfy the three conditions for a subset to be a subspace:
(i) The subset must contain the zero vector.
(ii) The subset must be closed under vector addition.
(iii) The subset must be closed under scalar multiplication.
Let S be a subset of V consisting of arithmetic sequences.
Now we check the three conditions :
(i) We find an arithmetic sequence in S that has all its terms equal to zero. The only arithmetic sequence that satisfies this is the sequence (0, 0, 0, 0, ...), which is in S.
So , the subset "S" contains zero vector.
(ii) Next we need to show that if u and v are two arithmetic sequences in S, then their sum "u + v" is also an arithmetic sequence in S.
Let U = (a, a+k, a+2k, a+3k, ...) and V = (b, b+l, b+2l, b+3l, ...) be two arithmetic sequences in S.
Then, their sum is ⇒ u+v = (a+b, a+k+b+l, a+2k+b+2l, a+3k+b+3l, ...).
This is also an arithmetic sequence,
So , subset "S" is closed under vector addition.
(iii) Next , we show that if U is an arithmetic sequence in S and C is a scalar, then CU is also an arithmetic sequence in S.
Let U = (a, a+k, a+2k, a+3k, ...) be an arithmetic sequence in S, and let c be a scalar.
we get , CU = (ca, ca+ck, ca+2ck, ca+3ck, ...) is also an arithmetic sequence,
So , subset "S" is closed under scalar multiplication.
we see that , S satisfies all three conditions, it is a subspace of V.
Therefore, any subset of V consisting of arithmetic sequences is a subspace of V.
Learn more about Subspace here
https://brainly.com/question/30318872
#SPJ4
The given question is incomplete , the complete question is
Let V be the space of all infinite sequences of real numbers , Which of the subsets of V in The arithmetic sequences [i.e. sequences of the form (a , a+k , a+2k , a+3k for some constants a and k] are subspaces of V ?
A.60
B.120
C.240
D.360

Answers
Answer:
b i think brainlest me plz
Step-by-step explanation:
Find the exact value of each of the remaining trigonometric functions of θ. Rationalize denominators when applicable.
secθ=−8, given that sinθ>0
Answers
The exact values of the remaining trigonometric functions of θ are:
sin(θ) = √(1/64)
cos(θ) = -8
tan(θ) = -8√(1/64)
csc(θ) = 1
cot(θ) = -√(1/64) / 8
Given that sec(θ) = -8 and sin(θ) > 0, we can find the exact values of the remaining trigonometric functions using the Pythagorean identity:
sec^2(θ) = 1/sin^2(θ)
Substituting the value of sec(θ), we have:
(-8)^2 = 1/sin^2(θ)
64 = 1/sin^2(θ)
sin^2(θ) = 1/64
sin(θ) = ±√(1/64)
Since sin(θ) > 0, we take the positive square root:
sin(θ) = √(1/64)
Next, we use the reciprocal identity for cosecant:
csc(θ) = 1/sin(θ)
Substituting the value of sin(θ), we have:
csc(θ) = 1/√(1/64) = 8√(1/64) = 8/√(64) = 8/8 = 1
Next, we use the reciprocal identity for cotangent:
cot(θ) = 1/tan(θ)
We can find the value of tan(θ) using the definition:
tan(θ) = sin(θ) / cos(θ)
Substituting the values of sin(θ) and cos(θ), we have:
tan(θ) = √(1/64) / (-8) = -√(1/64) / 8
Finally, we use the reciprocal identity for a tangent:
tan(θ) = 1/cot(θ)
Substituting the value of cot(θ), we have:
tan(θ) = -8√(1/64)
Therefore, the exact values of the remaining trigonometric functions of θ are:
sin(θ) = √(1/64)
cos(θ) = -8
tan(θ) = -8√(1/64)
csc(θ) = 1
cot(θ) = -√(1/64) / 8
The complete question is:-
Find the exact value of each of the remaining trigonometric functions of
θ. Rationalize denominators when applicable.
secθ=−8, given that sinθ>0
To learn more about trigonometric functions, refer:-
https://brainly.com/question/6904750
#SPJ4
Reflects -9, -7 across the x-axis then reflect the result across the Y axis what are the coordinates of a final point
Answers
So, reflecting (-9, -7) across the x-axis gives us (−9, 7).
When a point is reflected across the y-axis, the x-coordinate changes sign, while the y-coordinate remains the same.
So, reflecting (−9, 7) across the y-axis gives us (9, 7).
Therefore, the coordinates of the final point after reflecting (-9, -7) first across the x-axis and then across the y-axis is (9, 7).
a) (10 pts) Re-express the given differential equation as a first order differential equation by utilizing matrix
and vector notation and in accordance with ()
= () form.
b) (10 pts) Is the system obtained in (a) stable, neutrally stable of unstable? Determine this using matrix.
c) (10 pts) Compute the eigenvalues and eigenvectors of matrix.
d) (10 pts) Using the results computed in (c) find and matrices and show that =
−
relationship
(i.e., the diagonalization relationship) is a valid relationship.

Answers
a) To re-express the given differential equation as a first-order differential equation using matrix and vector notation, we can rewrite it in the form:
\(x' = Ax\)
where x is a vector and A is a square matrix.
b) To determine the stability of the system obtained in part (a), we need to analyze the eigenvalues of matrix A.
If all eigenvalues have negative real parts, the system is stable.
If at least one eigenvalue has a zero real part, the system is neutrally stable.
If at least one eigenvalue has a positive real part, the system is unstable.
c) To compute the eigenvalues and eigenvectors of matrix A, we solve the characteristic equation
\(det(A - \lambda I) = 0\),
where λ is the eigenvalue and I is the identity matrix.
By solving this equation, we obtain the eigenvalues.
Substituting each eigenvalue into the equation
\((A - \lambda I)v = 0\),
where v is the eigenvector, we can solve for the eigenvectors.
d) Once we have computed the eigenvalues and eigenvectors of matrix A, we can construct the diagonalization relationship as follows:
\(A = PDP^{(-1)}\)
where P is a matrix whose columns are the eigenvectors of A, and D is a diagonal matrix whose diagonal elements are the eigenvalues of A.
To show that this relationship is valid, we can compute \(PDP^{(-1)}\) and verify that it equals A.
For such more questions on differential equation
https://brainly.com/question/18760518
#SPJ8
Find the area of the triangle. 14 ft 15 ft
Answers
Answer:
210
Step-by-step explanation:
you have to multiple 15 by 14
Answer:
DO NOT MULTIPLY 15x14! THAT IS WRONG
Step-by-step explanation:
To find the area of a triangle the formula is 1/2 x b x h
If 15 and 14 is the base and height just do half of 15 x 14
so 15 x 14= 210/ divided by 2= 105
Formula for area of a circle= 1/2*b*h
I neeeeed heeeelp please

Answers
Answer:
10b/y^2
Step-by-step explanation:
Hope this helps! :)
Determine the turning points and distinguish between them when necessary y=x³ - 3x - 9x + 4
Answers
The turning points of the function y = x³ - 3x² - 9x + 4 are (3, -23) and (-1, 9).
To determine the turning points of the given function y = x³ - 3x² - 9x + 4, we need to find the critical points where the derivative of the function is equal to zero.
1. Find the derivative of the function:
y' = 3x² - 6x - 9
2. Set the derivative equal to zero and solve for x:
3x² - 6x - 9 = 0
3. Factorize the quadratic equation:
3(x² - 2x - 3) = 0
4. Solve the quadratic equation by factoring or using the quadratic formula:
(x - 3)(x + 1) = 0
This gives us two possible values for x: x = 3 and x = -1.
5. Substitute these critical points back into the original function to find the corresponding y-values:
For x = 3:
y = (3)³ - 3(3)² - 9(3) + 4
= 27 - 27 - 27 + 4
= -23
For x = -1:
y = (-1)³ - 3(-1)² - 9(-1) + 4
= -1 - 3 + 9 + 4
= 9
6. Therefore, the turning points are (3, -23) and (-1, 9).
Note: It appears that there was a typo in the original equation, where the term "-9x" should have been "-3x²". The above solution assumes the corrected equation.
For more such questions on points, click on:
https://brainly.com/question/26865
#SPJ8
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
Which of the following can you determine when you use deduction and start from a given set of rules and conditions
Answers
Answer:
What must be true
Step-by-step explanation:
What percent of the population is polled, if the population size is 4,000 at a NYC high
school and the sample size is 75?
Answers
Answer:
1.875 %
Step-by-step explanation:
Divide the sample size by the population then multiply by 100:
percent = (75 ÷ 4000) x 100 = 1.875 %
Plsss help me! Brainlist!!

Answers
Answer: = (the third option)
Step-by-step explanation
Answer:
the answer is this sign <!
Step-by-step explanation:
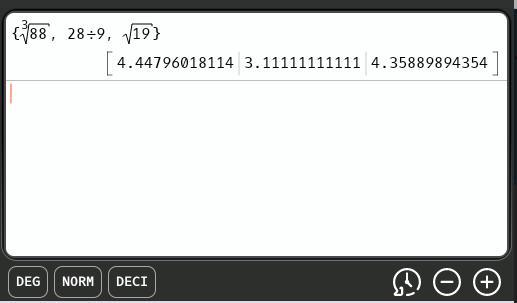
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1

A computer randomly puts a point inside the rectangle. What is the probability that the point lands in triangle T?
Answers
Answer:
87.5%
Step-by-step explanation:
The area of the entire rectangle is 8 by 6,
8x6=48 so the area is 48 units^2.
The area of the triangle is A=1/2bh
A=1/2(2)(6)
A=1(6)
A=6 units^2
6/48=0.125
0.125=12.5%
You need to find the percent it will not land in the triangle, so subtract 12.5 from 100.
100-12.5=87.5
There is an 87.5% chance it will not land in the triangle
Luct sold 8 cups of lemonade abbie sold 6 times as many cups of lemonade
Answers
The amount of cups of lemonade sold by Abbie is 6 x 8 = a.
Hence, option A is correct.
Use the concept of multiplication defined as:
To multiply means to add a number to itself a particular number of times. Multiplication can be viewed as a process of repeated addition.
Given that,
Number of lemonade cups sold by Lust = 8
Number of lemonade cups sold by Abbie = 6 times of lust
Let 'a' represents the number of cups sold by Abbie,
Therefore,
6 x 8 = a
Hence,
The correct expression is 6 x 8 = a which is option A.
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ3
The complete question is:
Luct sold 8 cups of lemonade Abbie sold 6 times as many cups of lemonade. Which equation helps us find how many cups Abbie sold if the number of cups sold by Abbie is 'a'.
A. 6x8 = a
B. 8xa = 6
C. 6xa = 8
What is the aquare route of 64
Answers
Answer:
square root of 64 is 8
Step-by-step explanation:
8^2=64
8*8=64
If
B
and
4 + 8
are the
root
of the Cauation
СТ
+ 6t -
and the value of c
Answers
Answer:
lol bro i hope these help u out
Step-by-step explanation:
good job me
10
Use the cards 1-10. Draw cards without replacing.
A.
B.
CÓ Ư
C.
D.
E.
F.
P(6, then 1)
P(even, then 5)
P(8, then odd)
P(3, then prime)
P(prime, composite)
P(even, then 3, then 5)
4
8
2
6
9
3
10

Answers
A. P(6, then 1) = 1/90
B. P(even, then 5) = 1/18
C. P(8, then odd) = 1/18
D. P(3, then prime) = 2/45
E. P(prime, composite) = 4/15
F. P(even, then 3, then 5) = 1/144
Given:
Total number of cards: 10
A. P(6, then 1):
P(6, then 1) = 1/10 x 1/9
= 1/90
B. P(even, then 5):
Number of favorable outcomes: 5 x 1 = 5
P(even, then 5) = 5/10 x 1/9
= 1/18
C. P(8, then odd):
Number of favorable outcomes: 1 x 5 = 5
P(8, then odd) = 1/10 x 5/9
= 1/18
D. P(3, then prime):
Number of favorable outcomes: 1 x 4 = 4
P(3, then prime) = 1/10 x 4/9
= 2/45
E. P(prime, composite):
Number of favorable outcomes: 4 x 6 = 24
P(prime, composite) = 4/10 x 6/9
= 4/15
F. P(even, then 3, then 5):
Number of favorable outcomes: 5 x 1 x 1 = 5
P(even, then 3, then 5) = 5/10 x 1/9 x 1/8
= 1/144
Learn more about Probability here:
brainly.com/question/32117953
#SPJ1
A rectangle has an area of 18 square centimeters.
Which of the following could be the rectangle's length and width?
(Area = length x width)
Choose all answers that apply:
B
C
1 cm and 18 cm
2 cm and 9 cm
3 cm and 6 cm
4 cm and 5 cm
Answers
Answer:
1 cm and 18 cm
2 cm and 9 cm
3 cm and 6 cm
Step-by-step explanation:
We need to find the factors of 18
which are; 1,18; 2,9; 3,6
So therefore we'd pick:
1 cm and 18 cm
2 cm and 9 cm
3 cm and 6 cm
Find the unit rate. 3/8 mile in 3/4 hour
Answers

We are required to find the unit rate, that is, miles per hour
The unit rate is 1/2 miles per hourNumber of miles = 3/8 mileNumber of hours = 3/4 hourTherefore, unit rate = = 3 / 8 ÷ 3/4= 3 / 8 × 4/3= 12/24= 1/2Read more:
https://brainly.com/question/8406966
Help please?! I don't understand what I need to do.

Answers
A) The maximum of the periodic function is 1.
B) The minimum of the periodic function is - 3.
C) The equation of the midline of this periodic function is (1 - 3)/2 = - 1.
D) The amplitude of the periodic function is (1 + 3)/2 = 2.
E) the period of the periodic function is 2π/3.
F) We know frequency = 2π/period = 2π/2π/3 = 2π×(3/2π) = 3.
G) The amplitude of the periodic function is 2sin3((πx - π/6)) - 1.
What is a periodic function?A period is the amount of time between two waves, whereas a periodic function is one whose values recur at regular intervals or periods.
A function f will be periodic with period x, so if we have
f (a + x) = f (a), For every a > 0.
A) The periodic function's maximum value is 1.
B) The periodic function's minimum value is -3.
C) This periodic function's midline's equation is (1 - 3)/2 = - 1.
D) The periodic function's amplitude is (1 + 3)/2 = 2.
E) The periodic function's period is 2π/3.
F) We already know that frequency = 2π/period
= 2π/2π/3 = 2π×(3/2π) = 3.
G) The periodic function is 2sin3((πx - π/6)) - 1.
learn more about periodic functions here :
https://brainly.com/question/29277391
#SPJ1