Figure ABCD is a parallelogram.
Parallelogram A B C D is shown. The length of A B is 3 y minus 2, the length of B C is x + 12, the length of D C is y + 6, and the length of A D is 2 x minus 4.
What are the lengths of line segments AB and BC?
AB = 4; BC = 16
AB = 4; BC = 8
AB = 10; BC = 20
AB = 10; BC = 28
Answers
The lengths of line segments AB and BC are AB = 10; BC = 28
What are parallelograms?Parallelograms are shapes with parallel and equal opposite sides
The given parameters are:
AB = 3y - 2
BC = x + 12
DC = y + 6
AD = 2x - 4
The above means that:
AB = DC
BC = AD
So, we have:
AB = DC
3y -2 = y + 6
Collect like terms
3y - y = 2 + 6
2y = 8
Divide by 2
y = 4
Also, we have:
BC = AD
x + 12 = 2x - 4
Collect like terms
2x - x = 4 + 12
x = 16
The lengths AB and BC are given as:
AB = 3y - 2
BC = x + 12
So, we have:
AB = 3*4 - 2
AB = 10
BC = x + 12
BC =16 + 12
BC = 28
Hence, the lengths of line segments AB and BC are AB = 10; BC = 28
Read more about parallelograms at:
https://brainly.com/question/24056495
Answer:
D
Step-by-step explanation:
Related Questions
FILL IN THE BLANK eigenvalues and eigenvectors of a matrix (optional) 0 points possible (ungraded) let , ____ and ____, where unanswered_____- , where unanswered . therefore, is an eigenvector of with eigenvalue , and is an eigenvector of with eigenvalue .
Answers
Let A be a matrix, v and λ be vectors. Therefore, Av = λv, where v is an eigenvector of A with eigenvalue λ, and if there is another non-zero vector w such that Aw = μw, then w is an eigenvector of A with eigenvalue μ. Therefore, v is an eigenvector of A with eigenvalue λ, and w is an eigenvector of A with eigenvalue μ.
Allow a to be a matrix, and v and λ to be vectors. Consequently, av = λv, wherein v is a non-zero vector and λ is a scalar. This means that v is an eigenvector of a with eigenvalue λ.
Further, if there may be every other non-0 vector w such that aw = μw, then w is an eigenvector of a with eigenvalue μ. The eigenvectors and eigenvalues of a matrix are vital in lots of packages, including fixing systems of linear equations, studying dynamical systems, and studying facts using strategies along with main thing evaluation.
By computing the eigenvectors and eigenvalues of a matrix, we will benefit perception of its shape and conduct, and use these records to solve problems and make predictions.
Learn more about eigenvalue:
brainly.com/question/29749542
#SPJ4
Due to the tide, the water level rises and falls daily in Buzzard's Bay. D gives the depth of the water, in meters, t hours after midnight on a certain day. What is the best interpretation for the following statement? The value of the derivative of D at t = 8 is equal to -0.5. Choose 1 answer a. At 8 a.m. the water level decreased at a rate of 0.5 meters per hour. b. At 8 a.m. the water level decreased at a rate of 0.5 meters. c. At 8 a.m. the water level was 0.5 meters below sea level. d. Until 8 a.m. the water level decreased at a rate of 0.5 meters per hour.
Answers
The correct interpretation for the statement D'(8) = -0.5 is (c) At 8 a.m. the water level was 0.5 meters below sea level.
How to interpret the function notation D'(n)From the question, we have the following parameters that can be used in our computation:
The function D gives the depth of the water, in meters, t hours after midnight on a certain day
This means that
D = depth in meters
t = time in hours
From the question, we have
Notation = D(n)
Also, from the question, we have
D'(8) = -0.5
This is the inverse of the function D(t)
So, the values of the parameters are
D(t) = -0.5
t = 8
This means that the number of hours is 8 and the depth is -0.5 meters
Hence, the interpretation of D'(8) = -0.5 is (c) At 8 a.m. the water level was 0.5 meters below sea level.
Read more about inverse functions at
brainly.com/question/3831584
#SPJ1
Huiling has sonme 20-cent coins and 50-cent coins. She has 4 times as many 20-cent coins as 50-cent coins. She has a total of $39. How many coins does she have altogether?
Answers
Answer: 150
Step-by-step explanation:
When writing a proof, how do you construct the first statement?
A) By writing the justification for the first statement in the right column.
B) By copying the “prove” statement(s) from the original problem.
C) By writing the next logical statement from the current one.
D) By copying the “given” statement(s) from the original problem.
Answers
When writing a proof, you should construct the first statement by copying the “prove” statement(s) from the original problem. The Option B is correct.
How should you construct the first statement in a proof?When constructing the first statement in a proof, it is important to begin with copying the “prove” statement(s) from the original problem. This involves writing the next statement based on the given or previously proven statements.
It is not helpful to write a justification for the first statement in the right column without considering its logical connection to the problem. By beginning with a logically connected statement, the proof can proceed in a clear and organized manner which leads to a valid conclusion.
Read more about proof
brainly.com/question/29969150
#SPJ1
20 points!
Please help.

Answers
2+2 brain time yessir
Answers
Answer:
Step-by-step explanation:
4 is the correct answer
Which reason explains why the triangles below are congruent?SSSSASAASASAHL or none of the above

Answers
We have the following:
Congruence criteria
The congruence criteria show us the minimum information necessary to affirm that two
triangles are congruent. They allow us to identify, with the available information, if two triangles
are or are not congruent with each other.
First congruence criterion: SSS
Two triangles are congruent if their three sides are respectively equal
Second congruence criterion: SAS
Two triangles are congruent if they have two sides and the angle between them respectively equal.
Third congruence criterion: ASA
Two triangles are congruent if they have one side and the two angles adjacent to that side respectively equal.
In this case we have that all the angles are equal, therefore, all their sides are equal, which means that it is an SSS congruence.
A manufacturer has 576 square inches of material available to construct the 6 faces of a carton, which will be in the shape of a rectangular prism. To maximize the volume, the carton will have dimensions such that the length and width are each twice the height.
Answers
To maximize the volume, of the rectangular prism, the carton should have dimensions of approximately 10.74 inches (length), 10.74 inches (width), and 5.37 inches (height).
What is the dimension required to maximize the volume of the box?Assuming the height of the rectangular prism is h inches.
According to the given information, the length and width of the prism will be twice the height, which means the length is 2h inches and the width is also 2h inches.
The total surface area of the rectangular prism is given by the formula:
Surface Area = 2lw + 2lh + 2wh
Substituting the values, we have:
576 = 2(2h)(2h) + 2(2h)(h) + 2(2h)(h)
576 = 8h² + 4h² + 4h²
576 = 16h² + 4h²
576 = 20²
h² = 576/20
h² = 28.8
h = √28.8
h = 5.37
The height of the prism is approximately 5.37 inches.
The length and width will be twice the height, so the length is approximately 2 * 5.37 = 10.74 inches, and the width is also approximately 2 * 5.37 = 10.74 inches.
Learn more on maximizing volume here;
https://brainly.com/question/10373132
#SPJ4
Answer correctly for brainlist

Answers
Answer:
Quadrilaterals
Step-by-step explanation:
Graph the equation using slope-intercept form (y=mx +b)
-3x + y = -2
Answers
both x-axis in the graph is before 5 or -5
SLOPE-INTERCEPT: y=3x-2
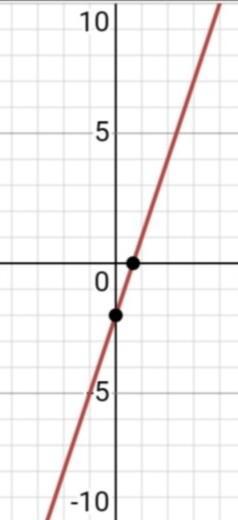

-3x+y=-2
y=3x-2

Use Stokes´ Theorem to evaluate ∬s.curl F•nds. Assume that the Surface S is oriented upward.
F= (6yz)i+(5x)j+ (yz(e^(x^2)))k. ; S that portion of the paraboloid z=(1/4)x^2+y^2 for 0≤z≤4
Answers
The surface integral in terms of ρ and θ ∫∫S.((6y - 5)e^(x^2))
To evaluate ∬s.curl F•nds using Stokes' Theorem, we first need to find the curl of the vector field F and then compute the surface integral over the given surface S.
Given vector field F = (6yz)i + (5x)j + (yz(e^(x^2)))k, let's find its curl:
∇ × F = ∂/∂x (yz(e^(x^2))) - ∂/∂y (5x) + ∂/∂z (6yz)
Taking the partial derivatives, we get:
∇ × F = (0 - 0) i + (0 - 0) j + (6y - 5)e^(x^2)
Now, let's parametrize the surface S, which is the portion of the paraboloid z = (1/4)x^2 + y^2 for 0 ≤ z ≤ 4. We can use cylindrical coordinates for this parametrization:
r(θ, ρ) = ρcos(θ)i + ρsin(θ)j + ((1/4)(ρcos(θ))^2 + (ρsin(θ))^2)k
where 0 ≤ θ ≤ 2π and 0 ≤ ρ ≤ 2.
Next, we need to find the normal vector n to the surface S. Since S is oriented upward, the normal vector points in the positive z-direction. We can normalize this vector to have unit length:
n = (∂r/∂θ) × (∂r/∂ρ)
Calculating the partial derivatives and taking the cross product, we have:
∂r/∂θ = -ρsin(θ)i + ρcos(θ)j
∂r/∂ρ = cos(θ)i + sin(θ)j + (1/2)(ρcos(θ))k
∂r/∂θ × ∂r/∂ρ = (-ρsin(θ)i + ρcos(θ)j) × (cos(θ)i + sin(θ)j + (1/2)(ρcos(θ))k)
Expanding the cross product, we get:
∂r/∂θ × ∂r/∂ρ = (ρcos(θ)(1/2)(ρcos(θ)) - (1/2)(ρcos(θ))(-ρsin(θ)))i
+ ((1/2)(ρcos(θ))sin(θ) - ρsin(θ)(1/2)(ρcos(θ)))j
+ (-ρsin(θ)cos(θ) + ρsin(θ)cos(θ))k
Simplifying further:
∂r/∂θ × ∂r/∂ρ = ρ^2cos(θ)i + ρ^2sin(θ)j
Now, we can calculate the surface integral using Stokes' Theorem:
∬s.curl F•nds = ∮c.F•dr
= ∫∫S.((∇ × F)•n) dS
Substituting the values we obtained earlier:
∫∫S.((∇ × F)•n) dS = ∫∫S.((6y - 5)e^(x^2))•(ρ^2cos(θ)i + ρ^2sin(θ)j) dS
We can now rewrite the surface integral in terms of ρ and θ:
∫∫S.((6y - 5)e^(x^2))
for such more question on surface integral
https://brainly.com/question/20771646
#SPJ8
The transformation T that transposes every matrix is definitely linear. Which of these extra properties are true? (a) T2 = identity transformation. (b) The kernel of T is the zero matrix. (c) Every matrix is in the range of T. (d) T (M) = -M is impossible
Answers
Option (a) T2 = identity transformation. (b) The kernel of T is the zero matrix. (c) Every matrix is in the range of T. this are true extra properties.
The transformation T that transposes every matrix is indeed linear.
Let's analyze each of the extra properties:
(a) T² = identity transformation: This is true. When you transpose a matrix twice (apply T twice), you get the original
matrix back.
Step 1: Apply T to a matrix M to get its transpose M'.
Step 2: Apply T to the transpose M' to get (M')' which is equal to M.
(b) The kernel of T is the zero matrix: This is true. The kernel of T consists of all matrices M such that T(M) = 0. Since the
transpose of a zero matrix is still a zero matrix, the kernel of T only contains the zero matrix.
(c) Every matrix is in the range of T: This is true. Given any matrix M, there exists another matrix M' such that T(M') = M.
This is because T(M') = M implies M' = T(M), so the transpose of any matrix M can be found by applying T to M.
(d) T(M) = -M is impossible: This is false. It is possible for T(M) = -M in the case of skew-symmetric matrices. A skew
symmetric matrix M satisfies the property that its transpose M' = -M.
for such more question on matrix
https://brainly.com/question/2456804
#SPJ11
Find that the radius of curvature of ^2y=x^3-a^3
at the point where the
curves cut the X-axis.
Answers
The radius of curvature of the curve \(a^{2y\)=x³-a³ at the point where the curve intersects the x-axis is 27\(a^{\frac{3}{2}\).
To find the radius of curvature of the curve \(a^{2y\)=x³-a³ at the point where the curve intersects the x-axis, we need to first find the equation of the curve and then determine the value of y and its derivative at that point.
When the curve intersects the x-axis, y=0. Therefore, we have:
a⁰ = x³ - a³
x³ = a³
x = a
Next, we need to find the derivative of y with respect to x:
dy/dx = -2x/(3a²√(x³-a³))
At the point where x=a and y=0, we have:
dy/dx = -2a/(3a²√(a³-a³)) = 0
Therefore, the radius of curvature is given by:
R = (1/|d²y/dx²|) = (1/|d/dx(dy/dx)|)
To find d/dx(dy/dx), we need to differentiate the expression for dy/dx with respect to x:
d/dx(dy/dx) = -2/(3a²(x³-a³\()^{\frac{3}{2}\)) + 4x²/(9a⁴(x³-a³\()^{\frac{1}{2}\))
At x=a, we have:
d/dx(dy/dx) = -2/(3a²(a³-a³\()^{\frac{3}{2}\)) + 4a²/(9a⁴(a³-a³\()^{\frac{1}{2}\)) = -2/27a³
Therefore, the radius of curvature is:
R = (1/|-2/27a³|) = 27\(a^{\frac{3}{2}\)
To learn more about radius of curvature click on,
https://brainly.com/question/31403088
#SPJ1
Find the value of x.
13)
O
(2x+8)
62°
20 22 Kuta Software LLC.
14)
A
(x-4) (2x+1)
All rights reserve d-1-Made with Infinite Geometry.
Answers
Answer:
Without additional information or context, it is not possible to find the value of x for the given diagrams. Please provide more information or the full problem statement.
What is the value of ?
T
80°
25°
R
?
P
PLEASE

Answers
9514 1404 393
Answer:
105°
Step-by-step explanation:
The exterior angle marked "?" is equal to the sum of the remote interior angles:
? = 25° +80°
? = 105°
By creating a General Court made up of delegates from each town in the colony, this document reflects the principle of:
federalism
individual rights
checks and balances
republicanism

Answers
By creating a General Court made up of delegates from each town in the colony, this document reflects the principle of: D. republicanism.
What is federalism?Federalism simply refers to a form of government in which the federal government and other institutional bodies such as states, towns, smaller units, and provinces share power and authority.
What is republicanism?Republicanism can be defined as a form of government that is centered around citizenship in a state and emphasizes their participation for the common good of a geographical area such as states, towns, and other smaller units in a colony.
This ultimately implies that, republicanism involves citizens selecting their representatives (delegates) from each town in a colony, especially through an electoral process such as in Article 8, Fundamental Orders of Connecticut.
Read more on republicanism here: https://brainly.com/question/5188360
#SPJ1
Answer:
republicanism
Step-by-step explanation:
f(x)=4x2−5x
as 1≤x≤7
.
Answers
Answer: 1<23
Step-by-step explanation:
A recent survey showed that exactly 38%
of people in a town buy the local
newspaper. There are 2450 people in the
town.
a) How many people in the town buy the
local newspaper?
b) How many people in the town do not
buy the local newspaper?
Answers
Answer:
a) .38 × 2,450 = 931 people buy the local newspaper.
b) 2,450 - 931 = 1,519 people do not buy the local newspaper.
Which of the following statements describes the graph below?
PLS HELP.

Answers
Answer:
piecewise, continuous.
Step-by-step explanation:
This is piecewise simply because it is in pieces. Thus PIECEwise (Pun intended). This is continuous because, as you can see, there is a filled in dot on the same x coordinate as every empty dot. The empty dots mean that that value is not in that part of the graph. However, since the other parts of the function "fill the gaps," then it is continuous. I hope this helps!
It's offcourse piecewise
For continuity
Observe the graph
The domain is like
(-oo,1]U(1,2]U(2,oo)For close ineterval there is an open interval hence it's continuous
Write equation (2,9) slope -3
Answers
Answer: y=-3x+15
Step-by-step explanation:
y=mx+b
9=(-3)(2)+b
b=15
y=-3x+15
The length of a rectangle is 3 inches more than its width. If the length and width are each increased by 2 inches, the perimeter of the rectangle becomes 66 inches. If x is the width of the rectangle, find its length and width.
Answers
Answer:1
Step-by-step explanation:
Ryu went shopping for new headphones he found a pair he wanted for $50.00. He found a discount code for 35%. How much did ryu save with this discount code
pls hurry I need this ASAP
will give first CORRECT answer brianliest
btw This is the TGA
Answers
Explanation: Two ways to look at it, 35% is the same as saying 35 hundredths or 0.35. We know that anytime there’s an of in a math problem it means multiply, so you multiply .35x50 and you get 17.5 or $17.50.
Explanation 2: you can look at the 50 as the 100%, so if you divide 100% by 100 you get 1% so that’s what we’re going to start with dividing the 50 by 100 and you get .5, and now that you have 1% you can multiply that by 35 to get the 35%. Which is 17.5
..........................................what's the exchange rate at the post office is £1

Answers
Answer:
€327.6
Step-by-step explanation:
==>Given:
Post office exchange rate=> £1 = €1.17
==>Required:
Amount of Euros that will get me £280
==>Solution:
Using the exchange rate at the list office as stated in the question, convert £280 to euros:
Let x be the amount in euros
£1 = €1.17
£280 = x
Cross multiply to equate
x*£1 = €1.17*£280
Divide both sides by £1 to make x the subject of formula
x = (€1.17*£280)/£1
x = €327.6
You will get €327.6 for £280
Solve for in the equation = .
Answers
Answer:
What's the equation?
Step-by-step explanation:
Russell is doing some research before buying his first house. He is looking at two different areas of the city, and he wants to know if there is a significant difference between the mean prices of homes in the two areas. For the 33 homes he samples in the first area, the mean home price is $168,300. Public records indicate that home prices in the first area have a population standard deviation of $37,825. For the 32 homes he samples in the second area, the mean home price is $181,900. Again, public records show that home prices in the second area have a population standard deviation of $25,070. Let Population 1 be homes in the first area and Population 2 be homes in the second area. Construct a 95% confidence interval for the true difference between the mean home prices in the two areas.
Answers
Answer:
The 95% confidence interval for the true difference between the mean home prices in the two areas is (-$29156.52, $1956.52).
Step-by-step explanation:
Before building the confidence interval, we need to understand the central limit theorem and subtraction of normal variables.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Subtraction between normal variables:
When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.
First area:
33 homes, mean of $168,300, standard deviation of $37,825. Thus:
\(\mu_1 = 168300\)
\(s_1 = \frac{37825}{\sqrt{33}} = 6584.5\)
Second area:
33 homes, mean of $181,900, standard deviation of $25,070. Thus:
\(\mu_2 = 1819000\)
\(s_2 = \frac{25070}{\sqrt{32}} = 4431.8\)
Distribution of the difference:
\(\mu = \mu_1 - \mu_2 = 168300 - 181900 = -13600\)
\(s = \sqrt{s_1^2+s_2^2} = \sqt{6584.5^2 + 4431.8^2} = 7937\)
Confidence interval:
\(\mu \pm zs\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
95% confidence level
So \(\alpha = 0.05\), z is the value of Z that has a p-value of \(1 - \frac{0.05}{2} = 0.975\), so \(Z = 1.96\).
The lower bound of the interval is:
\(\mu - zs = -13600 - 1.96*7937 = -29156.52 \)
The upper bound of the interval is:
\(\mu + zs = -13600 + 1.96*7937 = 1956.52\)
The 95% confidence interval for the true difference between the mean home prices in the two areas is (-$29156.52, $1956.52).
Identifying the center and radius to graph

Answers
Answer:
center is (5/2,2) and the radius is 4
Step-by-step explanation:
show that a) cos3∅=cos²∅-3cos∅sin²∅
Answers
The correct proof of the equation is cos3θ =cos(2θ + θ) = cos²θ - 3cosθsin²θ (Proved)
Solving trigonometry identity
Given the trigonometry identity below:
cos3∅=cos²∅-3cos∅sin²∅
We are to prove that both sides of the equation are equal.
cos 3θ = cos(2θ + θ)
Using the double angle formula for cosine, we can expand the first term:
cos(2θ + θ) = cos2θ cos θ - sin2θ sinθ
Since cos2θ = cos²θ - sin²θ
cos(2θ + θ) = cos²θ - sin²θ - 2cosθsinθsinθ
cos(2θ + θ) = cos²θ - sin²θ - 2cosθsin²θ
On simplifying, we can see that;
cos3θ =cos(2θ + θ) = cos²θ - 3cosθsin²θ (Proved)
Learn more on trigonometry here: https://brainly.com/question/7331447
#SPJ1
Isabel went to the grocery store. She spent $15.91 on vegetables and $11.22 on fruit. She also bought some bread. If she paid with 3 ten dollar bills and got 45 cents back in change, how much did she spend on bread?
Answers
Based on an equation, the amount that Isabel spent on bread was $2.42.
How the equation was solved?To solve the equation for the amount spent on bread, we determined the total amount Isabel spent by subtracting the change from the total bills she had.
An equation is a mathematical statement of the equality or equivalence of two or more mathematical expressions.
The amount Isabel spent on vegetables = $15.91
The amount she spent on fruits = $11.22
Let the amount she spent on bread = x
The total amount she went with = $30 (3 x $10)
The change she got after giving the cashier $30 = $0.45
The total amount Isabel spent for vegetables, fruits, and bread = $29.55 ($30.00 - $0.45)
x = $2.42 ($29.55 - $15.91 - $11.22)
Check:
Vegetables = $15.91
Fruits = $11.22
Bread = $2.42
Total expenses = $29.55
Learn more about equations at https://brainly.com/question/29174899.
#SPJ1
How many unique values can be created by forming the fraction $\frac{x}{y}$ where $x$ is either 4, 8, or 12 and $y$ is either 4, 8, or 12?
Answers
Answer:
7 unique values can be created.
\(1,2,3,\dfrac{1}{2},\dfrac{1}{3},\dfrac{2}{3},\dfrac{3}{2}\)
Step-by-step explanation:
We need to find unique values that can be created by forming the fraction
\(\dfrac{x}{y}\)
where, \(x\) is either 4, 8, or 12 and \(y\) is either 4, 8, or 12.
Now, possible ordered pairs are (4,4), (4,8), (4,12), (8,4), (8,8), (8,12), (12,4), (12,8), (12,12).
For these ordered pairs the value of \(\dfrac{x}{y}\) are:
\(\dfrac{4}{4},\dfrac{4}{8},\dfrac{4}{12},\dfrac{8}{4},\dfrac{8}{8},\dfrac{8}{12},\dfrac{12}{4},\dfrac{12}{8},\dfrac{12}{12}\)
\(1,\dfrac{1}{2},\dfrac{1}{3},2,1,\dfrac{2}{3},3,\dfrac{3}{2},1\)
Here, 1 is repeated three times. So, unique values are
\(1,2,3,\dfrac{1}{2},\dfrac{1}{3},\dfrac{2}{3},\dfrac{3}{2}\)
Therefore, 7 unique values can be created.
Which equation correctly shows the relationship between the numbers 6,560 and 656?
Answers
Answer:
656×1000
Step-by-step explanation: