Find point
on the x-axis so that AC + BC is a minimum.
A(4,-5), B(12,3)

Four technicians make repairs when breakdowns occur on an automated production line. 20% of the breakdowns are serviced by Janet, 60% of the breakdowns are serviced by Tom, 15% of the breakdowns are serviced by Georgia, and 5% of the breakdowns are serviced by Peter.

When making repairs, each technician has a chance of making an incomplete repair. Janet makes an incomplete repair 1 time in 20, Tom makes an incomplete repair 1 time in 10, Georgia makes an incomplete repair 1 time in 10, and Peter makes an incomplete repair 1 time in 20.

If the next problem with the production line is diagnosed as being due to an initial repair that was incomplete, we can find the probability that the initial repair was made by each technician as follows:
- Probability that the initial repair was made by Janet: (20/100) x (1/20) = 0.001
- Probability that the initial repair was made by Tom: (60/100) x (1/10) = 0.006
- Probability that the initial repair was made by Georgia: (15/100) x (1/10) = 0.0015
- Probability that the initial repair was made by Peter: (5/100) x (1/20) = 0.00025

Therefore, the probability that the initial repair was made by Janet is 0.001, the probability that it was made by Tom is 0.006, the probability that it was made by Georgia is 0.0015, and the probability that it was made by Peter is 0.00025. The total probability is 0.00875.

To know more about production line visit:

https://brainly.com/question/26966565

#SPJ11

Answer:

The odd answer

is d

This is because 90 + 48 + c gives us 138

and so its not trye

Answer:

A

Step-by-step explanation:

perpendicular lines are the negative reciprocals of each other, and a pair of these lines intersects at 90 degrees.

Answer:

D. y=-6x+3

Step-by-step explanation:

the equations have the same slope of -6 which makes them perpendicular

the probability that the sample mean breaking strength for a random sample of 40 rivets is between 10,000 and 10,300 P(10000 ≤ x ≤ 10300) = 0.54

We would assume a normal distribution for the breaking strength of a rivet. We would apply the formula for normal distribution which is expressed as

z = (x - µ)/σ/√n

Where

n = number of samples

x = Breaking strengths of rivet.

µ = mean breaking strength

σ = standard deviation

From the information given,

µ = 10,100 psi

σ = 499 psi

n = 40

The probability that the sample mean breaking strength for a random sample of 40 rivets is between 10000 and 10,300 is expressed as

P(10000 ≤ x ≤ 10300)

For x = 10000,

z = (10000 - 10100)/499/√40 = - 0.13

Looking at the normal distribution table, the probability corresponding to the z score is 0.45

For x = 10300,

z = (10300 - 10100)/499/√40 = 2.54

Looking at the normal distribution table, the probability corresponding to the z score is 0.99

Therefore,

P(10000 ≤ x ≤ 10300) = 0.99 - 0.45 = 0.54

learn more about of probability here

https://brainly.com/question/15248399

#SPJ4

We have verified Chebyshev’s inequality for k = 2 and k = 3 when x ∼ binomial(50, 0.4).

Main answer :Using r’s "pbinom" function, we can verify Chebyshev’s inequality for k = 2 and k = 3 when x ∼ binomial(50, 0.4).The P(X ≤ μ + 2σ) and P(X ≤ μ + 3σ) values were obtained from the "pbinom" function for k = 2 and k = 3, respectively.

Supporting explanation :Chebyshev’s inequality states that for any data set, the proportion of the data within k standard deviations of the mean is at least 1 – 1/k^2, where k is a constant greater than 1. This holds true regardless of the shape of the distribution. To verify Chebyshev’s inequality for k = 2 and k = 3 when x ∼ binomial(50, 0.4), we first calculate the mean and standard deviation using the formula μ = np and σ = sqrt(npq), where n = 50, p = 0.4, and q = 0.6. Thus, μ = 20 and σ = 2.83.Then, we use the "pbinom" function in R to obtain the values of P(X ≤ μ + 2σ) and P(X ≤ μ + 3σ) for k = 2 and k = 3, respectively. For k = 2, P(X ≤ 25.66) = 0.9975, and for k = 3, P(X ≤ 28.49) = 0.9995.These values are greater than or equal to 1 – 1/k^2, where k = 2 and k = 3, respectively.

Know more about Chebyshev’s inequality here:

https://brainly.com/question/30928440

#SPJ11

Answer: 14.73091

Step-by-step explanation:

The square root of 217, (or root 217), is the number which when multiplied by itself gives the product as 217. Therefore, the square root of 217 = √217 = 14.730919862656235.

Triangle EBC have interior angles and exterior angles. The three appropriate options to the given question are:

B. Angle DEC is an exterior angle

C. Angle ABE and EBC are supplementary angles

E. Angle BEC is a remote interior angle to exterior angle BCF​

An exterior angle is one that lies outside a given figure. Thus, it is not an interior angle of the figure. While an interior angle is an angle within the boundaries of the figure.

Supplementary angles are two or more angles whose measures add up to the value of angle on a straight line (i.e \(180^{o}\)).

Thus considering the given triangle EBC, the appropriate options to the question are:

B. Angle DEC is an exterior angle

C. Angle ABE and EBC are supplementary angles

E. Angle BEC is a remote interior angle to exterior angle BCF​

These three options best describes the relationships among the angles of the triangle.

Visit: https://brainly.com/question/23327304

Answer:

bce

Step-by-step explanation:

took the test

The rounded potential volume of the tank is approximately 348,700.9 cubic feet, making the approximate volume of the tank 348,700.9 cubic feet.

To calculate the potential volume of the tank (cylinder), we need to know the radius of the base. However, the given information only provides the circumference of the tank and the height. We can use the circumference to find the radius, and then use the radius and height to calculate the volume of the cylinder.

Let's proceed with the calculations step by step:

Step 1: Find the radius of the tank's base

The formula for the circumference of a cylinder is given by:

C = 2πr, where C is the circumference and r is the radius.

Given that the circumference is approximately 295.3 feet, we can solve for the radius:

295.3 = 2πr

Divide both sides by 2π:

r = 295.3 / (2π)

Calculate the value of r using a calculator:

r ≈ 46.9 feet

Step 2: Calculate the volume of the cylinder

The formula for the volume of a cylinder is given by:

V = π\(r^2h\), where V is the volume, r is the radius, and h is the height.

Substitute the values we have:

V = π(\(46.9^2)(40)\)

V = π(2202.61)(40)

Calculate the value using a calculator:

V ≈ 348,700.96 cubic feet

Step 3: Round the volume to the nearest tenth

The potential volume of the tank, rounded to the nearest tenth, is approximately 348,700.9 cubic feet.

Therefore, the potential volume of the tank is approximately 348,700.9 cubic feet.

For more such information on: volume

https://brainly.com/question/31439709

#SPJ8

Answer:

She made 138, 179 two point field goals and 118

3-point field goals during the regular season

Step-by-step explanation:

Answer:

118, 138, and 179 points

Step-by-step explanation:

x = 3-point goals

2-point goals = 2x - 57

free throws = 2x - 57 - 41

3x + 2x * (2x - 57) + (2x - 57 - 41) = 850

3x + 4x - 114 + 2x - 98 = 850

9x = 1062

x = 118

2x - 57 = 2 * 118 - 57 = 179

2x - 57 - 41 = 138

Answer:

The sum of 2 + 2 is 4

Step-by-step explanation:

A federal study reported that 7.5% of the u.s. workforce has a drug problem

a-1. You would expect 1.5 of the 20 employed workers in the sample to have a drug problem.

a-2. The standard deviation for this problem would be 1.1180.

b. The likelihood that none of the workers sampled has a drug problem is 0.3679.

c. The likelihood that at least one of the workers sampled has a drug problem is 1 - 0.3679 = 0.6321.

Using drugs may result in dependency and addiction, as well as physical and mental health concerns, difficulties sleeping, and other negative outcomes. Your usage of drugs has an effect not just on you but also on the people around you.

a-1. It is reasonable to anticipate that 1.5 of the 20 employed people in the sample will have a problem with drugs.

a-2: The value of 1.1180 would be used to represent the standard deviation for this situation.

a. The probability that any of the employees who were surveyed struggle with substance abuse is 0.3679.

c. The probability that at least one of the employees who have sampled struggles with substance abuse is 1 less than 0.3679, which equals 0.6321.

Read more about the drug problem

https://brainly.com/question/957216=

#SPJ1

Answer:

km is a unit of distance

and si unit of distance is meters.(m)

1 km = 10³ m

•°• 2 km = 2 × 10³ m

in SI unit 2km = 2 × 10³ m or 2000 m

Using pythagorean theorem the area of the rectangle in terms of n is given by A = n√(324 - n^2).

In the given scenario, we have a circle with a diameter that is twice the length of the radius, which is stated as 18. The diagonal of the rectangle is also the diameter of the circle, so it measures 18. Let's assume the width of the rectangle as 'w'. By applying the Pythagorean theorem, we can establish the following relationship:\(n^2 + w^2 = 18^2\) = 324, where 'n' represents the length of the rectangle.

To solve for 'w', we rearrange the equation: \(w^2 = 324 - n^2.\) This equation allows us to calculate the width 'w' of the rectangle when we know the length 'n'.

The area of the rectangle, denoted as 'A', is given by the formula A = nw, where 'n' is the length and 'w' is the width of the rectangle. By substituting the expression for w^2, we obtain: A =\(n\sqrt(324 - n^2).\)

This equation represents the relationship between the length 'n' and the area 'A' of the rectangle, taking into account the given information about the diameter of the circle, which is also the diagonal of the rectangle. By solving for 'n' and substituting it into the formula, we can determine the area of the rectangle.

Let the width of the rectangle be w, then by the Pythagorean theorem, we have:

\(n^2 + w^2 = 18^2\) = 324

Solving for w, we get: \(w^2 = 324 - n^2\)

The area of the rectangle is given by:

A = nw

Substituting the expression for w^2, we get:

A =\(n\sqrt(324 - n^2)\)

To know more about pythagorean theorem refer to

https://brainly.com/question/343682

#SPJ11

A form of digital television that works with digital broadcast signals, transmitting digital sound, supporting wide screens, and providing high resolutions is High-Definition Television (HDTV).

HDTV is a type of television broadcasting that utilizes digital signals, allowing for superior picture and sound quality compared to traditional analog television. It supports wide screens, providing an aspect ratio of 16:9, which is ideal for displaying content in widescreen formats. HDTV also offers high resolutions, typically 720p or 1080i/p, resulting in sharper and more detailed images on compatible high-definition displays. With its digital nature, HDTV brings improved audiovisual experiences to viewers, enhancing their overall television-watching experience.

Learn more about ratio here:

https://brainly.com/question/31945112

#SPJ11

Answer: D. x+2/x^3+2

Step-by-step explanation:

x2+x−2/x3−x2+2x−2

x2+x−2/x3−x2+2x−2

(x−1)(x+2)/(x−1)(x2+2)

x+2/x2+2

Answer:

15<m

Step-by-step explanation:

7<2m-23

+23. +23

30<2m-0

30<2m

30/2<2/2

15<m

To find the amount of oatmeal in ounces for 1 ounce of milk, we use the following proportion

Now, we solve for x.

So, for 1 ounce of milk, the amount of oatmeal is 4/5 ounces.

Now, let's find the amount of milk for 5 1/10 ounces of oatmeal.

Now, we solve for x

Hence, there are needed 6 3/8 ounces of milk to get 5 1/10 ounces of oatmilk.

The inversion of the Sackur-Tetrode equation yields the expression for the internal energy U(S, V, N) of an ideal gas. By using the thermodynamic identity, expressions for temperature T, pressure p, and chemical potential µ can be derived. The ideal gas law pV = NkBT is verified through this derivation.

The Sackur-Tetrode equation for the entropy of an ideal gas is:

S = Nk [ ln (V/N (4πmU/3Nh²\()^{3/2}\)) + 5/2 ]

Inverting this equation to obtain U(S, V, N)

U = 3/2 (S/Nk - 5/2 k ln(V/N(4πm/3Nh²\()^{3/2}\))

Next, using the thermodynamic identity U = TdS − pdV + µdN, we can derive expressions for T, p, and µ:

T = (∂U/∂S)|V,N = 3/2 k[(∂S/∂S)|V,N] = 3/2 k

p = - (∂U/∂V)|S,N = NkT/V

µ = (∂U/∂N)|S,V = -5/2 kT ln(V/N(4πm/3Nh²\()^{3/2}\))

Finally, we can verify the ideal gas law pV = NkBT by substituting the expression for T into the expression for p, giving:

pV = NkT/V * V = NkT

which is consistent with pV = NkBT. Thus, we have derived the expression for U(S, V, N), as well as expressions for T, p, and µ, and verified the ideal gas law.

To know more about ideal gas law:

https://brainly.com/question/13821925

#SPJ4

Step-by-step explanation:

a= - 5 - b

Subs. the above into...

ab = - 24

(-5-b)b = - 24

Therefore b=-24 or b=19

Answer:

see explanation

Step-by-step explanation:

Given the 2 equations

a + b = - 5 → (1)

ab = - 24 → (2)

Rearranging (1) expressing a in terms of b, that is

a = - 5 - b → (3)

Substitute a = - 5 - b into (2)

b(- 5 - b) = - 24 ← distribute left side

- 5b - b² = - 24 ( subtract - 5b - b² from both sides )

0 = b² + 5b - 24 ← in standard form

0 = (b + 8)(b - 3) ← in factored form

Equate each factor to zero and solve for b

b + 8 = 0 ⇒ b = - 8

b - 3 = 0 ⇒ b = 3

Substitute these values into (3) for corresponding values of a

b = - 8 : a = - 5 - (- 8) = - 5 + 8 = 3

b = 3 : a = - 5 - 3 = - 8

Thus

a = 3, b= - 8 or a = - 8, b = 3

The slope intercept form of a line which passes through the points (-2, 5) and (6, -4)  is  y = (-9/8)x + 11/4.

According to the question.

A line passes through the two points (-2, 5) and (6, -4).

As we know that, the slope intercept formula y = mx + b is used when you know the slope of the line to be examined and the point given is also the y intercept (0, b). In the formula, b represents the y value of the y intercept point.

So, the slope of the line = -4 -5/(6 + 2) = -9/8

And, the slope intercept form of a line which passes through the points (-2, 5) and (6, -4) is given by

y = (-9/8)x + b

Since, the line passes through (-2, 5) and (6, -4). So, both the points must statisfy the above equation.

⇒ 5 = (-9/8)(-2) + b

⇒ 5 = 9/4 + b

⇒ b = 5 - 9/4

⇒ b = (20 - 9)/4

⇒ b = 11/4

Therefore, the slope intercept form of a line which passes through the points (-2, 5) and (6, -4)  is  y = (-9/8)x + 11/4.

Find out more information about slope intercept form of a line here:

https://brainly.com/question/9682526

#SPJ4

Answer:

0.85

Step-by-step explanation:

17/20 = 85/100 = 0.85

Answer:

52°

Step-by-step explanation:

it should always add up to 180°

We may build up a proportion and solve for the scale model radius of Neptune using the ratio between the radii of the two planets and the known scale model radius of the Earth. The scale model of Neptune that is produced has a radius of around 9.7 cm.

We may take advantage of the fact that the ratio between the two planets' radii and the ratio between their respective scale model radii is the same. Let's name the Neptune scale model radius "r" Then, we may set up the ratio shown below:

Neptune's radius is equal to the product of Earth's radius and its scale model.

With the provided values, we may simplify and obtain:

24620 km / 6370 km equals 2.5 cm / r

We obtain the following when solving for "r":

r = (24620 km * 2.5 cm) / (6370 km)

r ≈ 9.7 cm

Therefore, a scale model of Neptune would have to be drawn with a radius of approximately 9.7 cm.

Learn more about scale models here:

https://brainly.com/question/17581605

#SPJ4

Explanation:

Label the slots A,B,C for first through third place.

There are 8 choices for slot A, 7 for slot B, and 6 for slot C. We start with 8 and count our way down until we get to the final slot. Then we multiply out those values

8*7*6 = 336

There are 336 ways to select three people from a pool of eight overall.

-----------------

If you want to use the permutation formula, then your steps might look like this

\(_n P _r = \frac{n!}{(n-r)!}\\\\_8 P _3 = \frac{8!}{(8-3)!}\\\\_8 P _3 = \frac{8!}{5!}\\\\_8 P _3 = \frac{8*7*6*5!}{5!}\\\\_8 P _3 = 8*7*6\\\\_8 P _3 = 336\\\\\)

Note how the 5! terms cancel out on the second to last step, leaving behind the expression 8*7*6 which was found earlier.

Answer:

15 long-sleeved shirts can be ordered.

Step-by-step explanation:

x = amount of short-sleeved.

y = amount of long-sleeved.

10x + 12y = 300

10(12) + 12y = 300

120 + 12y = 300

12y = 300 - 120

12y = 180

y = 180 / 12

y = 15

Answer:

nonlinear

Step-by-step explanation:

because the axis is located below so its all gucci

Answer:

Nonlinear

Step-by-step explanation:

It's actually a parabola because it has a squared value.

Hope that helps and have a great day!

One example of a graph G where the chromatic number is equal to the largest vertex degree plus one (A + 1) is a complete graph with A + 1 vertices.

In a complete graph, every vertex is connected to every other vertex, so the degree of each vertex is A. Therefore, the chromatic number of this graph would be A + 1. Another example is a star graph, where one central vertex is connected to A vertices. In this case, the central vertex has a degree of A, and all the other vertices have a degree of 1. Again, the chromatic number of this graph would be A + 1.  Based on these examples, the type of graph that satisfies this condition is a graph where there is one vertex with the maximum degree A, and all other vertices have degree 1. (b) An example of a planar graph with a chromatic number of 4 is the graph known as the "wheel graph". The wheel graph consists of a central vertex (hub) connected to several other vertices (spokes), and all the spokes are also connected to each other. In the wheel graph, the central vertex has degree equal to the number of spokes plus 1, and all the other vertices (spokes) have a degree of 3. Therefore, the chromatic number of the wheel graph is 4. Visually, the wheel graph looks like a wheel with the hub at the center and the spokes radiating outwards, forming a cycle with additional edges connecting the hub to each spoke.

It's important to remember that these are just examples, and there can be other graphs that satisfy the given conditions.

To learn more about chromatic number click here: brainly.com/question/32065333

#SPJ11

The probability of producing three daughters in a family of three children is 1/8 or 12.5%. This assumes that the probability of having a daughter or a son is equal, and that the gender of each child is independent of the others.

In order to calculate the probability, we can consider all possible combinations of genders for the three children. There are eight possible outcomes: BBB, BBG, BGB, BGG, GBB, GBG, GGB, and GGG, where B represents a boy and G represents a girl.

Out of these eight outcomes, only one outcome (GGG) fulfills the requirement of having three daughters. Therefore, the probability of producing three daughters is 1 out of 8, or 1/8. This translates to a probability of 12.5%.

It's important to note that this calculation assumes equal probability of having a boy or a girl, and that the gender of each child is independent of the others. In reality, the probability of having a boy or a girl may not be exactly 50%, and the gender of one child may influence the gender of subsequent children in some cases.

Learn more about probability here:

https://brainly.com/question/32004014

#SPJ11

The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).

To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:

Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:

\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)

Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:

\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)

Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.

So, the differentiation of the entire equation is:

\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)

Now, let's rearrange the terms:

\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)

Simplifying further:

\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)

Factoring out:

\(\[(\frac{dy}{dx})(y - x) = 0 \]\)

Finally, solving:

\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)

Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.

Learn more about derivative

brainly.com/question/29144258

#SPJ11

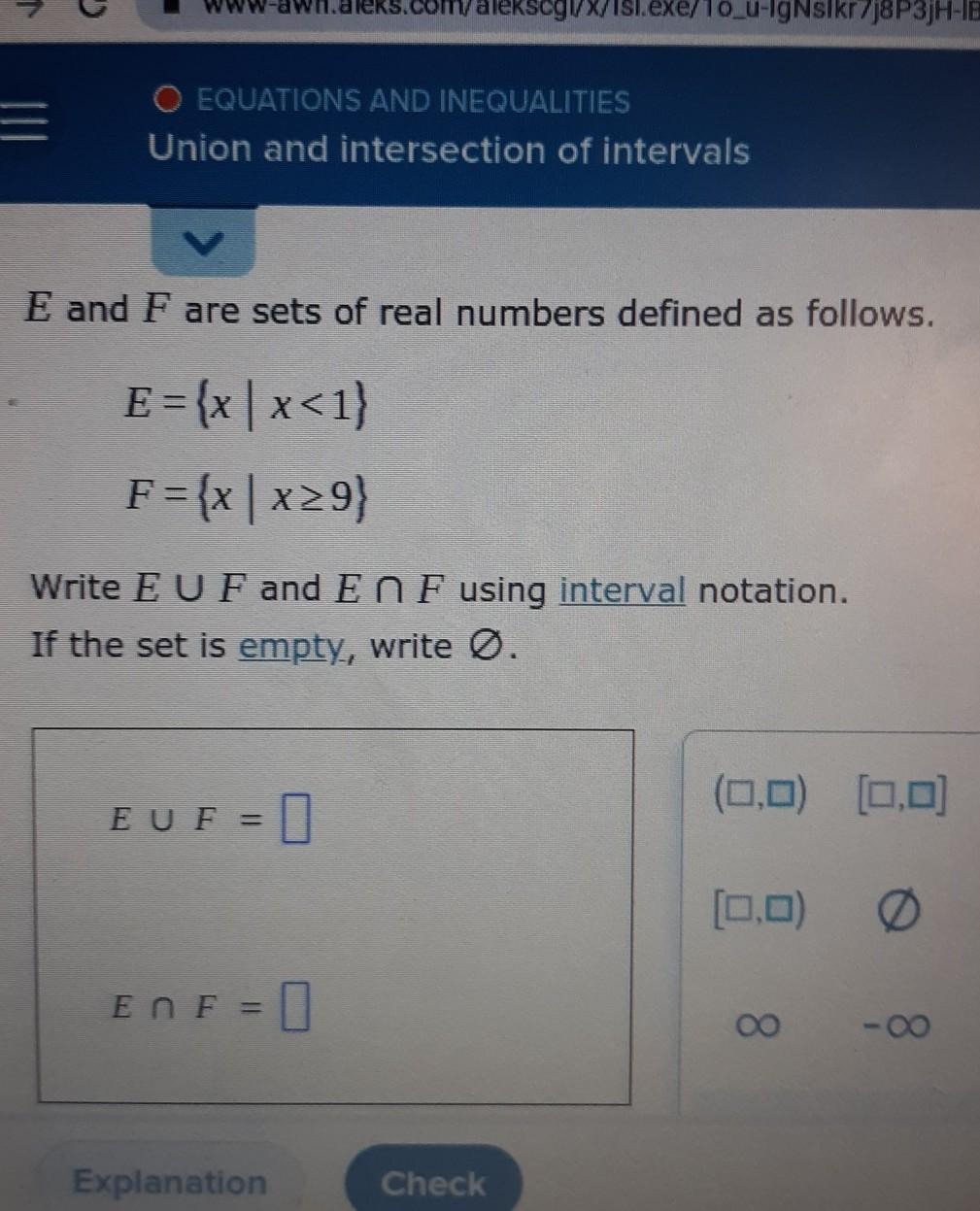
Answer:

Step-by-step explanation:

Union and intersection of intervals​

We are given the following intervals:

\(\mathbf{E}=\{x\mid x <1\}\)

\(\mathbf{F}=\{x\mid x \ge 9\}\)

We need to find the union and the intersection of the intervals.

Both intervals are represented in the number line as shown in the figure below.

The union of intervals is the set of elements that belong to any of the intervals.

Since both intervals have no common area:

\(E\cup F=(-\infty,1)\cup [9,+\infty)\)

The intersection of intervals is the set of elements that belong to all the intervals.

As pointed above, there is no common area, thus the intersection is empty

\(E\cap F=\o\)