Find the 8th term of the geometric sequence 6, 18, 54
Answers
6 • 3 = 18
18 • 3 = 54
54 • 3 = 162
162 • 3 = 486
486 • 3 = 1,458
1,458 • 3 = 4,374
4,374 • 3 = 13,122
Beginning at 6 as the initial value, we will find that the 8th term of this geometric sequence is 13,122.
Answer:
13122
Step-by-step explanation:
Term multiply by 3
First term is 6
Seven terms remain to be defined
then the 8th term is:
6 * 3⁷ = 6*2187
= 13122
Related Questions
Consider a Poisson probability distribution with λ = 5.1. Determine the following probabilities.
a) exactly 5 occurrences
b) more than 6 occurrences
c) 3 or fewer occurrences
Click the icon to view a partial table of Poisson probabilities.
a) The probability of exactly 5 occurrences is
(Round to four decimal places as needed.)
Answers
The probability of exactly 5 occurrences is (Rounding to three Decimal places), we get P(X ≤ 3) ≈ 0.251.
a) The probability of exactly 5 occurrences is given by the Poisson probability mass function:
P(X = 5) = (e^(-λ) * λ^5) / 5! = (e^(-5.1) * 5.1^5) / 120 ≈ 0.1755
Rounding to four decimal places, we get P(X = 5) ≈ 0.1755.
b) The probability of more than 6 occurrences can be calculated as the complement of the probability of 6 or fewer occurrences:
P(X > 6) = 1 - P(X ≤ 6) = 1 - (P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6))
Using the Poisson probability mass function and the given value of λ, we can calculate each of the probabilities:
P(X = 0) ≈ 0.006
P(X = 1) ≈ 0.031
P(X = 2) ≈ 0.079
P(X = 3) ≈ 0.135
P(X = 4) ≈ 0.174
P(X = 5) ≈ 0.1755
P(X = 6) ≈ 0.1493
Substituting these values into the formula, we get:
P(X > 6) ≈ 1 - (0.006 + 0.031 + 0.079 + 0.135 + 0.174 + 0.1755 + 0.1493) ≈ 0.249
Rounding to three decimal places, we get P(X > 6) ≈ 0.249.
c) The probability of 3 or fewer occurrences is given by the cumulative distribution function:
P(X ≤ 3) = ∑ P(X = k), for k = 0, 1, 2, 3.
Using the Poisson probability mass function and the given value of λ, we can calculate each of the probabilities:
P(X = 0) ≈ 0.006
P(X = 1) ≈ 0.031
P(X = 2) ≈ 0.079
P(X = 3) ≈ 0.135
Adding these probabilities, we get: P(X ≤ 3) ≈ 0.251
Rounding to three decimal places, we get P(X ≤ 3) ≈ 0.251.
To know more about probability
https://brainly.com/question/24756209 .
#SPJ11
Which is the equation of a line that has a slope of 1/2 and passes through point (2, -3)?
Y=1/2x-4, Y=1/2x-2, Y=1/2x+2, Y=1/2x+3
Answers
Answer:
y=1/2x-4
Step-by-step explanation:
y=1/2x+b
-3=1/2(2)+b
-3=1+b
-4=b
y=1/2x-4
Let the random variable X be equal to the number of days that it takes a high-risk driver to have an accident. Assume that X has an exponential distribution. If P(X < 50) = 0.25, compute P(X > 100 | X > 50).
Answers
The detailed answer of this question is:
P(X > 100 | X > 50)=0.455
Given that X follows an exponential distribution, we know that the probability density function (PDF) of X is given by:
f(x) = λe^(-λx) for x ≥ 0
where λ is the rate parameter of the distribution.
We are given that P(X < 50) = 0.25. Using the cumulative distribution function (CDF) of X, we can write:
P(X < 50) = 1 - e^(-λ*50) = 0.25
Solving this equation for λ, we get:
λ = -ln(0.75)/50 ≈ 0.0278
Now, we are asked to find P(X > 100 | X > 50). Using the definition of conditional probability, we can write:
P(X > 100 | X > 50) = P(X > 100 and X > 50) / P(X > 50)
= P(X > 100) / P(X > 50)
= e^(-λ100) / e^(-λ50)
= e^(-λ*50)
Substituting the value of λ, we get:
P(X > 100 | X > 50) = e^(-0.0278*50) ≈ 0.455
Therefore, the probability that a high-risk driver will have an accident after 100 days given that they have not had an accident for the first 50 days is approximately 0.455.
To know more about Exponential Function visit:
https://brainly.com/question/28596571
#SPJ4
HURRY !!
Write an equation for the graph in slope-intercept form.
Do not use spaces in the equation.
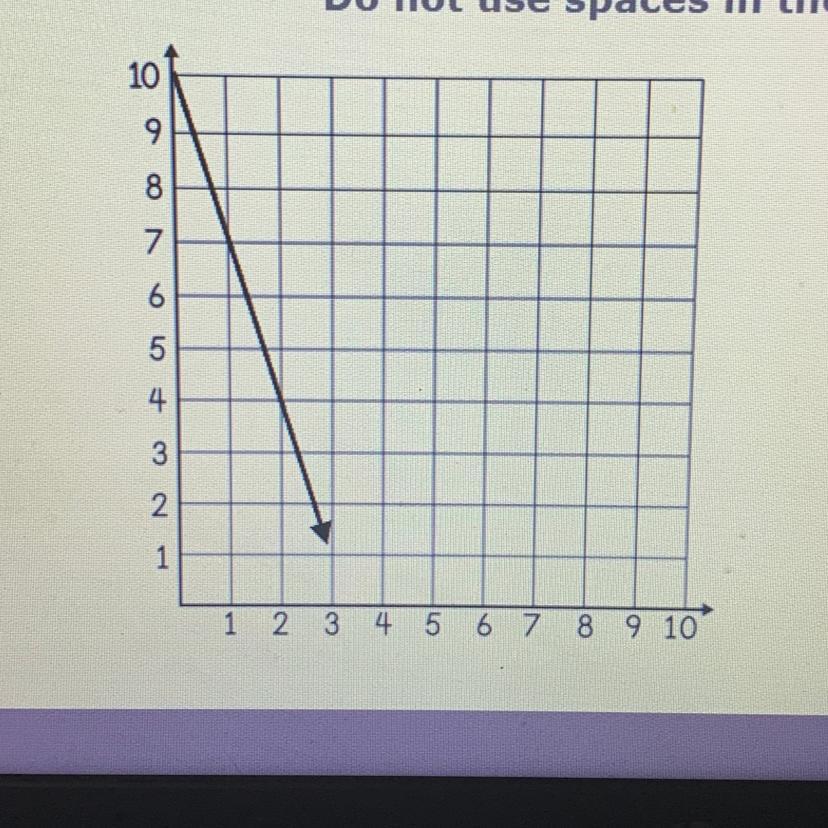
Answers
The equation for graph in slope intercept form is y=-3x+10.
Given the points from the graph are:
(0,10) = (x₁ , y₁)
(3,1) = (x₂ , y₂)
slope of the given points is :
m = (y₂ - y₁)/(x₂ - x₁)
m = (1 - 10)/(3 - 0)
m = -9/3
m = -3
equation of the line is : y - y₁ = m(x-x₁)
we have m = -3
and point = (0,10)
therefore, y - 10 = (-3)(x-0)
y-10=-3x+0
y=-3x+10
hence the slope intercept form is :
y=mx+c
therefore, y=-3x+10
hence we get the equation of the line as y=-3x+10
Learn more about Slope intercept form here:
brainly.com/question/1884491
#SPJ1
What is 1/10 if 7000
Answers
Answer:
700
Step-by-step explanation:
PLEASE HELP find the ratio of 25 cents to $1.25
Answers
Can someone please help me with this?

Answers
Answer:
65 mm²
Step-by-step explanation:
Total surface area of the prism = area of all parts of the prism's net
✔️Area of rectangle 1 with the following dimensions:
L = 5.2 mm
W = 2.1 mm
Area = 5.2*2.1 = 10.92 mm²
✔️Area of rectangle 1 with the following dimensions:
L = 5.2 mm
W = 4.5 mm
Area = 5.2*4.5 = 23.4 mm²
✔️Area of rectangle 3 with the following dimensions:
L = 5.2 mm
W = 5 mm
Area = 5.2*5 = 26 mm²
✔️Area of the 2 traingles with the following dimensions:
b = 4.5 mm
h = 2.1 mm
Area = ½*bh
= ½*4.5*2.1
= 4.725 mm²
Total surface area = 10.92 + 23.4 + 26 + 4.725 = 65.045 ≈ 65 mm² (nearesth while number)
Can someone fill this out thanks

Answers
20 Per Question, Algebra 2, Thanks :)





Answers
The answer to the expression is (x+3)/(x-1)
What is a quadratic expression?You should recall that a quadratic expression is an algebraic expression of the form ax2 + bx + c = 0, where a ≠ 0
The given expressions are
(x² - 3x - 18) / (x²- 7x +6
(x²-6x +3x +19) / (x²-x -6x +6)
This implies that {(x²-6x)+(3x-18)} / {(x²-x) -(6x+6)}
⇒[x(x-6)+3(x-6)] / [x(x-1) - 6(x-1)]
This means that [(x+3)(x-6)] / [(x-6)(x-1)]
Dividing by (x-6) to have
Therefore the value of the expression is (x+3)/(x-1)
Learn more about quadratic expression on https://brainly.com/question/31368124
#SPJ1
2. True or false? You can only use graphing find the solution to a system of equations if all
the equations are linear.
True
False
Answers
Answer:
False
Step-by-step explanation:
Graphing tells you where the solution of the system, or graph intersection occurs no matter what. You can have a quadratic and exponential function -- graphing will always show you where they intersect (or don't!)
BRAINLIEST please if this helped!Answer:
false
Step-by-step explanation:
hope this helps
What is the probability of at least two coins landing on heads? startfraction 5 over 16 endfraction startfraction 3 over 8 endfraction one-half startfraction 11 over 16 endfraction.
Answers
Answer:
.25 or 25%
Step-by-step explanation:
A sample of 100 gadgets is selected from one day’s production of 5,000 gadgets. In the sample, 7 are defective. Predict the number of gadgets in the day’s production that are not defective.
Answers
We can use the proportion of defective gadgets in the sample to estimate the number of defective gadgets in the entire production, and then subtract that from the total number of gadgets produced to estimate the number of non-defective gadgets.
The proportion of defective gadgets in the sample is:
7/100 = 0.07
We can assume that this proportion is representative of the entire production, so we can estimate the number of defective gadgets in the entire production as:
0.07 x 5000 = 350
Therefore, we can estimate the number of non-defective gadgets in the production as:
5000 - 350 = 4650
Therefore, we can predict that there are 4,650 gadgets in the day's production that are not defective.
Find dy/dx (the derivative ) of f(x) = 4x
2
using
limits definition of the derivitive (of limit of the
DQ when h> 0
Formulas needed
a) Equation of a line in slopeyintercept form y = f(x) = mx + b
b) Equation of a line slopepoint y y1 = m (x x1)
Answers
Derivative are used to determine the nature of a function. The derivative of the function f(x) = 4x^2 is 8x
Derivative of a functionThe formula for finding the derivative of a function is expressed as:
f'(x) = nax^n-1
Given the function expressed as:
f(x) = 4x^2
We are to find its derivative as shown:
f'(x) = 2(4)x^2-1
f'(x) = 8x^1 = 8x
Hence the derivative of the function f(x) = 4x^2 is 8x
Learn more on derivative here: https://brainly.com/question/416343
The gas tank of Dave car has a capacity of 12 gallons. The tank was 3/8 full before Dave filled it to capacity. It cost him $2.50 per gallon of gas . How much did Dave spend , in dollars, to fill the tank to capacity?
Answers
Answer: $18.75
Step-by-step explanation:
1 - 3/8 = 5/8
12 x 5/8 = 7.5
7.5 x 2.5 = 18.75
Dave spent $18.75, in filling his car's tank of capacity 12 gallons up to the capacity, which was 3/8th filled already, at the unit rate of $2.50 per gallon of gas.
What is the unit rate?The unit rate is the quantity (cost/distance/time, etc.) for one unit of another quantity (cost/distance/time, etc.).
How to solve the question?In the question, we are informed that the gas tank of Dave's car has a capacity of 12 gallons. The tank was 3/8 full before Dave filled it to capacity. It cost him $2.50 per gallon of gas.
We are asked the amount Dave spent.
The unit rate of gas is $2.50 per gallon.
To find the total amount spent by Dave, we need to find the volume of gas he filled and then multiply that volume with the unit rate.
The capacity of Dave's car's tank = 12 gallons.
Gas it already had = 3/8th of capacity,
or, gas it already had = 3/8 * 12 = 4.5 gallons.
Therefore, the volume of gas Dave filled = 12 - 4.5 gallons = 7.5 gallons.
The amount spent by Dave = Volume filled*Unit rate = $ 7.5 * 2.5 = $18.75.
Therefore, Dave spent $18.75, in filling his car's tank of capacity 12 gallons up to the capacity, which was 3/8th filled already, at the unit rate of $2.50 per gallon of gas.
Learn more about unit rates at
https://brainly.com/question/13994187
#SPJ2
please help!!! only 20 mins left

Answers
The rule of (x, y) → (-x, y), which is reflection over y-axis.
Given that, ΔABC maps to triangle ΔA'B'C'.
What is the reflection on y-axis?When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is taken to be the additive inverse. The reflection of point (x, y) across the y-axis is (-x, y).
The coordinate points of ΔABC are A(-4, 3), B(-3, -3) and C(1, 2) and the coordinate points of ΔA'B'C' are A'(4, 3), B'(3, -3) and C'(-1, 2).
Here, A(-4, 3) → A'(4, 3), x-coordinate is negated and y-coordinate remains same.
Similarly, B(-3, -3) → B'(3, -3) and C(1, 2) → C'(-1, 2) follows the same pattern.
From this, it is clear that the coordinates of triangle ABC is reflected on y-axis.
Therefore, the rule of (x, y) → (-x, y), which is reflection over y-axis.
To learn more about the reflection over y-axis visit:
https://brainly.com/question/15175017.
#SPJ1
Some number added to -11 is 37. Divide this number by -12. Then, multiply by -8. What is the final number?
Answers
Answer:
32
Step-by-step explanation:
Let the number be x
x + (-11) = 37
x - 11 = 37
x = 37 + 11
x = 48
Divide this number by -12. This will be:
= 48/-12
= -4
Then, multiply by -8. This will be:
= -4 × -8
= 32
Question 3 of 10
which choice is equivalent to the quotient
According to the property
below?
O A -5
B. 25
C5
OD. - 5
ES

Answers
Answer: D: Square Root Of 5
Step-by-step explanation: 30/6 is 5, now fill in the sqrt symbol. Hope this helped. (This problem was one of the simpler, friendlier numbers.)
Find two square numbers that total 45
Answers
x^2+^2=45
if ×=3 and y=6
then 9+36=45
a circular logo has a 72 degree sector shaded orange and a 129 degree sector shaded blue. The radius of the logo is 10 inches. What is the total area shaded orange and blue?
Answers
I don't know the answer so help
HELO PLEASE HELP ME WITH THIS I BADLY NEED THIS RN I'LL MARK AS BRA!NLIEST!! SOLVE THE VARIABLES!! IT'S OKAY IF YOU ONLY ANSWER 1 BUT PLEASE PUT THE SOLUTION!!

Answers
(1) The missing sides of the right triangle is r = 8√2, and t = 8.
(2) The missing sides of the right triangle cannot be determined.
(3) The missing sides of the right triangle is 60√2.
(4) The missing sides of the right triangle is y = 20, and z = 20√3.
(5) The missing sides of the right triangle is m = 2, and n = 4.
(6) The missing sides of the right triangle is p = 5√3, and O = 5.
What are the values of the missing sides of the right triangle?The values of the missing sides of the right triangle is calculated as follows;
For question 1; the lengths of the right triangle is calculated as;
sin 45 = 8/r
r = 8/sin 45
r = 8√2
tan 45 = t/8
t = 8 tan(45)
t = 8
For question 2;
The value of g cannot be determined since we don't know if the triangle is a right triangle.
For question 3; the lengths of the right triangle is calculated as;
Assuming the triangle is 45, 45, 90 triangle, then the value of x is calculated as;
sin 45 = 60/x
x = 60/sin 45
x = 60√2
For question 4; the lengths of the right triangle is calculated as;
sin 30 = Y/40
Y = 40 x 0.5
Y = 20
cos 30 = z/40
z = 40 x cos30
z = 20√3
for question 5; the lengths of the right triangle is calculated as;
tan 30 = m/2√3
m = 2√3 x tan30
m = 2
sin 30 = m/n
n = m/sin30
n = 2/0.5
n = 4
For question 6; the lengths of the right triangle is calculated as;
sin 60 = p/10
p = 10 x sin60
p = 5√3
sin 30 = O/10
O = 10 x sin(30)
O = 5
Learn more about sides of right triangles here: https://brainly.com/question/1248322
#SPJ1
using the disk method, determine the volume of a solid formed by revolving the region bounded above by the line , on the left by the line , on the right by the curve , and below by the line the about the -axis.
Answers
The volume of a solid formed by revolving the region bounded above by the line is (932π/15)
To use the disk method, we need to integrate over the axis of revolution, which is the y-axis in this case. We can break the solid into vertical disks of thickness dy.
The radius of each disk is given by the distance between the y-axis and the curve \(x = y^2 - 1\). So the radius is:
\(r = y^2 - 1\)
The height of each disk is the difference between the y-coordinate of the top curve y = 3 and the y-coordinate of the bottom curve y = 1. So the height is:
h = 3 - 1 = 2
The volume of each disk is then:
\(dV = \pi r^2h dy\)
Substituting r and h, we have:
\(dV = \pi (y^2 - 1)^2 (2) dy\)
To find the total volume, we integrate over the range of y from 1 to 3:
\(V = \int_{1}^{3} \pi(y^2 - 1)^2 (2) dy\)
This integral can be simplified by expanding the squared term:
\(V = \int_{1}^{3} \pi (y^4 - 2y^2 + 1) (2) dyV = 2\pi \int_{1}^{3}(y^4 - 2y^2 + 1) dyV = 2\pi [(1/5)y^5 - (2/3)y^3 + y]^3_1\)
V = \(2\pi [(1/5)(3^5 - 1^5) - (2/3)(3^3 - 1^3) + (3 - 1)]\)
V = 2π [(1/5)(242) - (2/3)(26) + 2]
V = 2π [(242/5) - (52/3) + 2]
V = 2π [(726/15) - (260/15) + 30/15]
V = 2π [(466/15)]
V = (932π/15)
To learn more about Disk method :
https://brainly.com/question/29891838
#SPJ4
Note: The full question is
Use the disk method or the shell method to find the volumes of the solids generated by revolving the region bounded by the graphs of the equations about the given lines. y = 1, y = 3, x = y^2 - 1.
Steve drove for 4 1/2 hours at 68 mph, how far did Steve drive?
Answers
Distance = speed x time
Distance = 68 x 4 1/2
Distance = 306 miles
Answer: 306 miles
Step-by-step explanation:
Speed= distance/time
Distance= speed•time
Time= distance/speed
Find the area of the rectangle on this centimetre grid.
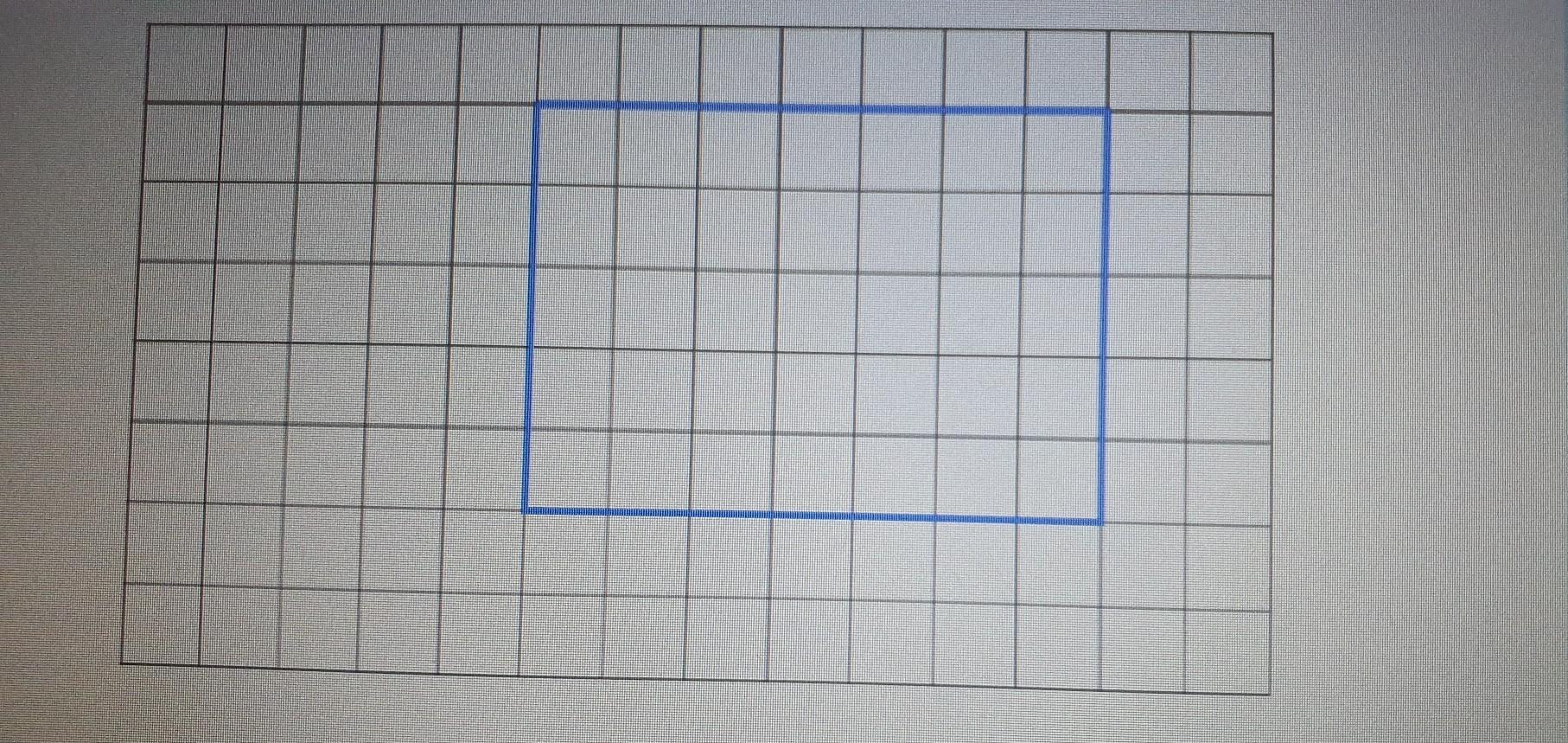
Answers
Answer:
A = 35 cm²
Step-by-step explanation:
the area (A) of a rectangle is calculated as
A = length × width
by counting the squares on the sides
length = 7 cm and width = 5 cm , then
A = 7 × 5 = 35 cm²
Which ratio is equivalent to 5:2?
7:4
2:5
10:4
5:1
Submit
Answers
Answer:
10:4
Step-by-step explanation:
..................
B. The estimate of the product is 7 OC. The estimate of the product is 10. D. The estimate of the product is 5. 1 oo lo X7 N(Type a whole number, fraction, or mixed number 7 . vo Enter your answer in the answer box and then click Check Answer. All parts showing

Answers
When we divide mixed numbers we need to first convert it from mixed fractions to improper ones and then we divide them. When we divide fractions a common guideline is to conserve the first fraction and multiply it by the inverse of the second one. With this in mind let's solve the problem.
\(\begin{gathered} (2+\frac{2}{3})\colon(4+\frac{1}{4}) \\ (\frac{6}{3}+\frac{2}{3})\colon(\frac{16}{4}+\frac{1}{4}) \\ \frac{8}{3}\colon\frac{17}{4} \\ \frac{8}{3}\cdot\frac{4}{17} \\ \frac{32}{51} \end{gathered}\)The answer to this division is 32/51
Find the area of the polygon. 4 cm 8 cm 8 cm 2 cm 2 cm 4 cm . . . Question content area right Part 1 The area of the polygon is
Answers
Answer:
the answer is 28 bc 2+2+4+4+8+8=28 so you answer will be twenty eight centi meters
Solve the equation 42 = v + 35 for v.
A. −77
B. 77
C. −7
D. 7
Answers
Answer:
v = 7
Step-by-step explanation:
42 = v + 35
-35 -35
7 = v
The answer is D. 7
I took the quiz and got it right
If your original biconditional statement is true, would the contrapositive be true? Give an example to illustrate your reasoning. '
Answers
Answer:
Step-by-step explanation:
es, if the original biconditional statement is true, then its contrapositive is also true.
Example: "If it rains, the grass is wet."
The contrapositive of this statement would be "If the grass is not wet, then it didn't rain."
Both the original statement and its contrapositive have the same truth value, as they are logically equivalent.
You have a pickle recipe that requires 24 ounces of sugar. You want to make a triple batch of pickles. How many pounds of sugar do you need for the triple batch?
Answers
Answer:
Step-by-step explanation:
4.5
The number of the pounds of sugar that you need for triple batch will be 72 ounces.
What are ratio and proportion?A ratio is a collection of ordered integers a and b represented as a/b, with b never equaling zero. A proportionate expression is one in which two items are equal.
You have a pickle recipe that requires 24 ounces of sugar.
You want to make a triple batch of pickles.
Then the number of the pounds of sugar that you need for triple batch will be
⇒ 3 x 24
⇒ 72 ounces
More about the ratio and the proportion link is given below.
https://brainly.com/question/14335762
#SPJ2
-16.3=w+6.1 first to answer will earn brainiest!
Answers
Answer:
w = - 22.4
Step-by-step explanation:
w + 6.1 = -16.3
**subtract 6.1 on both sides to isolate w:
w = -16.3 - 6.1
w = -22.4
Answer:i wont answer it because the other guy is right
Step-by-step explanation: