find the absolute maximum and absolute minimum values of f on the given interval. f(x) = 4x3 − 6x2 − 144x 9, [−4, 5]
Answers
The absolute maximum value of f on the interval [-4, 5] is 1,157 and the absolute minimum value of f on the interval [-4, 5] is -311.
To find the absolute maximum and absolute minimum values of f on the given interval, we need to follow the given steps:Step 1: Calculate the derivative of f(x)Step 2: Determine the critical points by setting the derivative equal to zero and solving for x.Step 3: Determine the intervals that need to be tested for local and absolute maxima and minima.
This can be done by creating a sign chart for the derivative.Step 4: Test each interval using the first or second derivative test to determine if the critical point is a local maximum or minimum, or if there is an absolute maximum or minimum on that interval.Step 5: Compare all the local and absolute maximum and minimum values to find the absolute maximum and absolute minimum values of f on the given interval.
The interval that needs to be tested for absolute maxima and minima is [-4, 5].We can create a sign chart for the derivative using the critical points to determine the intervals that need to be tested:Interval 1: (-∞, -3)Interval 2: (-3, 4)Interval 3: (4, ∞)f′(x) + − + − f(x) decreasing decreasing increasing Therefore, the interval (-3, 4) needs to be tested using the first or second derivative test.We can find the second derivative of f(x) as:f′′(x) = 24x − 12f′′(4) = 72 > 0Therefore, x = 4 is a local minimum on the interval (-3, 4).
To know more about interval visit :
https://brainly.com/question/30882226
#SPJ11
Related Questions
this graph represents the function f(x)=4sin(x) which statement is true about this function

Answers
Answer:
A
Step-by-step explanation:
The function is increasing in the interval in A because as the x-values increase so do the y-values on the graph, which can be shown by the graph sloping upwards at that specific section.
The graph of a function is increasing on the interval (3π/2, 2π) option (A) is correct.
What is trigonometry?Trigonometry is a branch of mathematics that deals with the relationship between sides and angles of a right-angle triangle.
We have given a graph of a trigonometric function,
As we know, the trigonometric function is sinusoidal in nature, and it has a domain of all real numbers and lies between the [a, a]where is the amplitude of the function.
The trigonometric ratio is defined as the ratio of the pair of a right-angled triangle.
From the graph, the function is increasing from 3π/2 to 2π
The graph slopes upward at that particular segment, indicating that the function is increasing in the interval in A as the x-values increase and the y-values on the graph follow suit.
Thus, the graph of a function is increasing on the interval (3π/2, 2π) option (A) is correct.
Learn more about trigonometry here:
brainly.com/question/26719838
#SPJ5
△DEF∼△XYZ Solve for x.
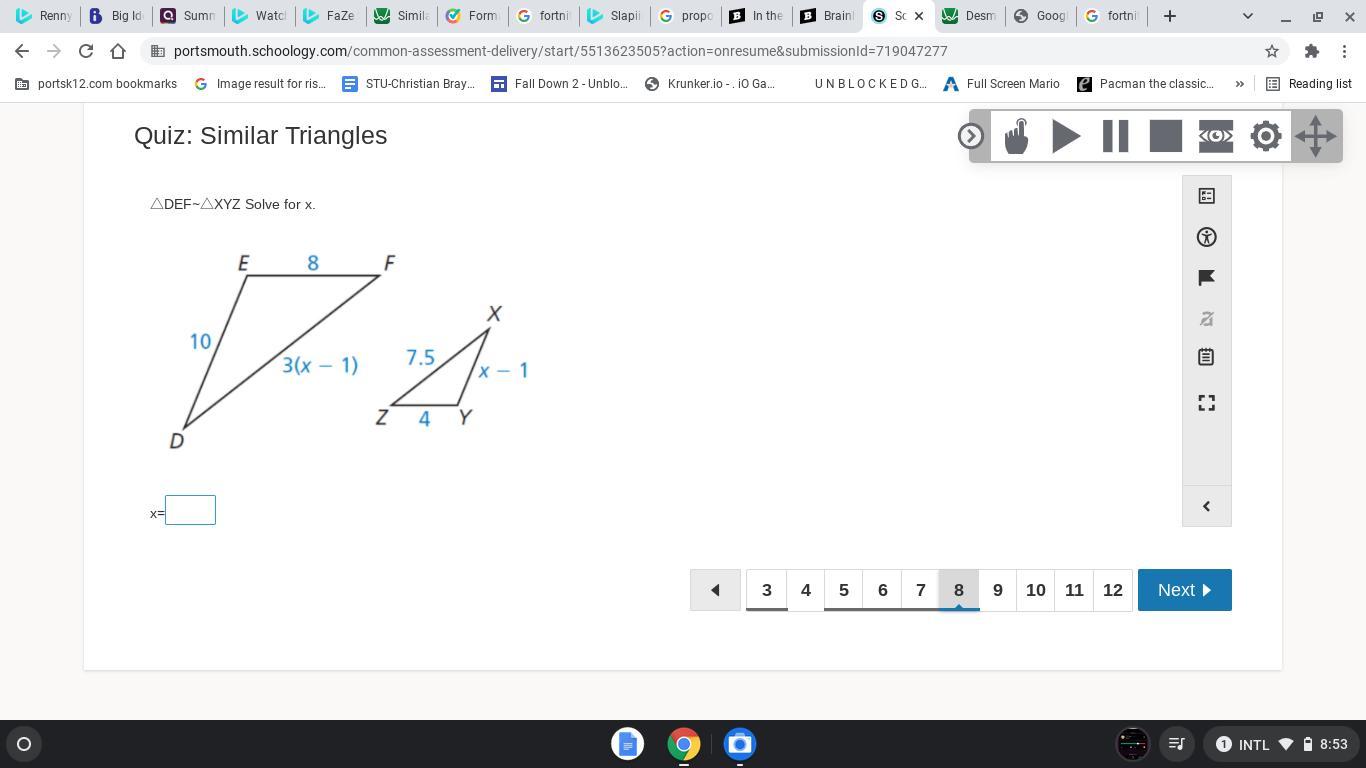
Answers
Answer:
x = 6
Step-by-step explanation:
Since the triangles are similar then the ratios of corresponding sides are in proportion, that is
\(\frac{DE}{XY}\) = \(\frac{EF}{YZ}\) , substitute values
\(\frac{10}{x-1}\) = \(\frac{8}{4}\) = 2 ( multiply both sides by x - 1 )
2(x - 1) = 10 ( divide both sides by 2 )
x - 1 = 5 ( add 1 to both sides )
x = 6
a= 5.2 B=70
Work out the area of the triangle. Round your answer to 1 DP

Answers
Answer:
8.7
Step-by-step explanation:
Calculate the area of the triangle by using sine.
Area of Triangle
\(A = \frac{1}{2} \times \text{side} \times \text{side} \times \sin{\theta}\)
θ ... included angle between the two sides
We already have two sides a and another side which is congruent to a, making it isosceles triangle. But we don't have the included angle. The angle we need is the vertex angle of the isosceles triangle. Angle B is one of the base angles (two base angles are congruent) and it measures 70°.
Recall that angles in any triangle add up to 180°.
base angle + base angle + vertex angle = 180°
70° + 70° + vertex angle = 180°
vertex angle = 40°
Now we have all the information to use the formula!
\(A = \frac{1}{2} \times \text{side} \times \text{side} \times \sin{\theta}\)
\(A = \frac{1}{2} \times 5.2 \text{ cm} \times 5.2 \text{ cm} \times \sin{40^\circ}\)
\(A = 13.52 \text{ cm}^2 \times \sin{40^\circ}\)
\(A \approx 8.6904 \text{ cm}^2\)
Rounded to 1 DP:
\(A = 8.7 \text{ cm}^2\)
Harry catches the train from Belfast to Dublin at 4pm.
The average speed of the train is 70mph and the distance from Belfast to Dublin is 105 miles.
What time does Harry arrive in Dublin?
Answers
Answer:
5:30 pm
Step-by-step explanation:
105/70 = 1.5
*10 points* ANSWER ASAP WILL MARK AS BRAINLIEST!!
Do you have to regroup to find each sum?
Choose Yes or No.
38 + 12
29 + 15
28 + 7
27 + 12
Answers
Answer:
1) yes
2)yes
3) yes
4) no
Step-by-step explanation:
let y= 6 −9 4 , u1= −3 −5 1 , u2= −1 1 2 . find the distance from y to the plane in ℝ3 spanned by u1 and u2.
Answers
The distance from y to the plane is:
distance = |47| / √30
= 47 / √30 (approximate value)
To find the distance from point y to the plane in ℝ³ spanned by u₁ and u₂, we can use the formula for the distance between a point and a plane. The formula is:
distance = |(y - p) · n| / ||n||
where y is the given point, p is a point on the plane, n is the normal vector to the plane, · denotes the dot product, and ||n|| represents the magnitude of the normal vector.
First, let's find the normal vector n by taking the cross product of u₁ and u₂:
n = u₁ x u₂
Calculating the cross product:
n = (-3, -5, 1) x (-1, 1, 2)
= (-32 - (-51), -12 - 1(-3), (-11 - (-31))
= (-1, -5, 2)
Now, let's choose a point on the plane. Since the plane is spanned by u₁ and u₂, any linear combination of u₁ and u₂ will lie on the plane. Let's choose the origin (0, 0, 0) as the point on the plane (p).
Using the formula, the distance from y to the plane is:
distance = |(y - p) · n| / ||n||
= |(6, -9, 4) · (-1, -5, 2)| / ||(-1, -5, 2)||
Calculating the dot product:
(6, -9, 4) · (-1, -5, 2) = 6*(-1) + (-9)(-5) + 42
= -6 + 45 + 8
= 47
Calculating the magnitude of the normal vector:
||(-1, -5, 2)|| = √((-1)^2 + (-5)^2 + 2^2)
= √(1 + 25 + 4)
= √30
Therefore, the distance from y to the plane is:
distance = |47| / √30
= 47 / √30 (approximate value)
Please note that the approximate value depends on the specific decimal approximation used for √30.
learn more about "distance ":- https://brainly.com/question/26550516
#SPJ11
As of 2019, there were about `210000000` adults in the United States.
On average, they each purchased `60` clothing items per year.
About how many clothing items did all of the adults in the United States purchase in 2019?
Answers
Answer:
Step-by-step explanation:
60= (total number of clothing items purchased)/ 210000000
total number of clothes purchased = 60*210,000,000= 12,600,000,000
If f(x) = 2x2 – 2, what is
X, what is f(-6)
give the right answer for a brilliant!
Answers
Answer:
f(- 6) = 70
Step-by-step explanation:
To evaluate f(- 6) , substitute x = - 6 into f(x)
f(- 6) = 2(- 6)² - 2 = 2(36) - 2 = 72 - 2 = 70
Answer:
\( \sf \: f( - 6) = 70\)
Step-by-step explanation:
Given function,
→ f(x) = 2x² - 2
Now we have to,
→ Find the required value of f(-6).
Then the value of f(-6) will be,
→ f(x) = 2x² - 2
→ f(-6) = 2(-6)² - 2
→ f(-6) = 2(36) - 2
→ f(-6) = 72 - 2
→ [ f(-6) = 70 ]
Hence, the value of f(-6) is 70.
Determine the infinite limit. x+2 lim *444x14 -[infinity] 8100 Need Help? Submit Answer Read It Watch It h
Answers
Given that x + 2 lim * 444x14 - [infinity] 8100, we are supposed to find the infinite limit. The solution to this problem is given below.
We are given that x + 2 lim * 444x14 - [infinity] 8100. The expression in the limit is in the form of (infinity - infinity), which is an indeterminate form.
To evaluate this limit, we need to rationalize the expression.
Let's multiply both numerator and denominator by the conjugate of the numerator.
Thus, the infinite limit of the given expression is x + 2.
Summary:Therefore, the infinite limit of the given expression x + 2 lim *444x14 - [infinity] 8100 is x + 2.
Learn more about conjugate click here:
https://brainly.com/question/11624077
#SPJ11
What is the unknown number?
Twelve us fourteen plus an unknown number
Answers
unknown number = -2
Let unknown number be n
12 = 14 + n
n + 14 = 12
n = 12 - 14
n = -2
an automobile insurance company divides customers into three categories: good risks, medium risks, and poor risks. assume that of a total of 11,102 customers, 7732 are good risks, 2421 are medium risks, and 949 are poor risks. as part of an audit, one customer is chosen at random. round your answers to four decimal places if necessary. a) the probability that the customer is a good risk is 0.70 . b) the probability that the customer is not a poor risk is
Answers
The probability that the customer is a good risk is 0.70 and the probability that the customer is not a poor risk is 0.957.
To calculate the probability of the customer being a good risk, we need to divide the total number of good risk customers (7732) by the total number of customers (11,102). This gives us 7732/11102 = 0.7000. To calculate the probability of the customer not being a poor risk, we can subtract the total number of poor risk customers (949) from the total number of customers (11,102). This gives us 11102-949 = 10,153. We then divide this number by the total number of customers, giving us 10,153/11,102 = 0.9571. Therefore, the probability that the customer is a good risk is 0.70 and the probability that the customer is not a poor risk is 0.9571.
Learn more about probability here
https://brainly.com/question/30034780
#SPJ4
PLEASE HURRY!!!!!!!
ILL GIVE BRAINLIEST!!!!!!!!!
NO LINKS!!!!!!!
CORRECT AND COMPLETE ANSWERS ONLY!!!!
Data regarding fuel efficiency of an 18-wheel truck were collected. The graph shows the correlation between the average speed above 40 miles per hour (in miles per hour) and the money spent on gas (in dollars):
image of a scatter plot with Average Speed on the x axis and Money Spent on Fuel on the y axis with points 1 comma 2, 3 comma 2 and one half, 5 comma 5, 7 comma 7, 9 comma 10, 11 comma 15, and 12 comma 17
Estimate the average rate of change from x = 5 to x = 9.
4
−4
1.25
Answers
Answer:
Give me a second, I just finished answering it, and trying to find a way to take a picture of it and send it to you.
Step-by-step explanation:
Graph -1,3 after rotation 90 degree clockwise around the orgin
Answers
Answer:
( 3,1)
Step-by-step explanation:
To rotate the point (-1, 3) 90 degrees clockwise around the origin, we can use the following formula:
(x', y') = (y, -x)
where (x, y) are the coordinates of the original point, and (x', y') are the coordinates of the rotated point.
So, for the point (-1, 3), we have:
x = -1
y = 3
Using the formula, we get:
x' = 3
y' = -(-1) = 1
Therefore, the coordinates of the point after rotation are (3, 1).
To graph this point, we can plot it on the coordinate plane. The point (3, 1) is located 3 units to the right of the origin and 1 unit above the origin.
The graph of the point (-1, 3) and its image (3, 1) after rotation 90 degrees clockwise around the origin is shown below:
|
| (3, 1)
|
|
------O------
|
|
|
| (-1, 3)
Help please due tomorrow

Answers
Answer: Its x^2 hope this helps
Step-by-step explanation:.
Answer:
a. 25
b. 34
Step-by-step explanation:
a). X²
if X=5
then
5²=25
b).(X +3)²
(5 +3)²
25+9
34
when isa travels to the usa for a holiday he leaves the uk at 1.00 pm local time and lands at 5.00 pm local time. on the return journey he leaves at 8.00 pm local time and lands at 10.00 am local time the next day. find the length of the flight in hours and the time difference between the uk and the part of the usa that isa visited
Answers
Isa took 4 hour when isa go from UK to USA and took 14 hour when she returns and time difference will be 10 hours
What is a definition distance?
the extent or amount of space between two things, points, lines, etc. the state or fact of being apart in space, as of one thing from another; remoteness
when isa travels to the usa for a holiday he leaves the uk at 1.00 pm local time and lands at 5.00 pm local time.
so isa took 4 hour
on the return journey he leaves at 8.00 pm local time and lands at 10.00 am local time the next day
isa tool 14 hour
find the length of the flight in hours and the time difference between the uk and the part of the usa that isa visited
length of flight is 18 hour
time difference will be 14-4 = 10 hour
learn more about time here
https://brainly.com/question/23973491
#SPJ4
Find the slope of the line segment shown.

Answers
The slope is the "rise over run" between any two points on the line.
Count out how much "up or down" vs "left or right" to find the slope:
We go up 5 and right 5, giving us the fraction
\(\dfrac{up~ 5}{right~ 5}=\dfrac{5}{5}=1\)
When counting, up and right are counted as positive; left and down are counted as negative.

Franklin took a total of 18 quizzes over the course of 6 weeks. How many weeks of school will Franklin have to attend this quarter before he will have taken a total of 30 quizzes? Solve using unit rates..
Answers
Franklin has to attend 10 weeks of school this quarter to have taken 30 quizzes.
The first step is the find the number of quizzes Franklin takes per week of school. To do that, use the formula:
= Number of quizzes / Number of weeks of school so far
= 18 / 6
= 3 quizzes per week
If Franklin gets 3 quizzes a week, to have 30 quizzes he will have to be in school for:
= Number of quizzes in total / Number of quizzes per week
= 30 / 3
= 10 weeks
Franklin will have to attend 10 weeks of school to write 30 quizzes.
Find out more at https://brainly.com/question/24572137.
Guys, I’m back from nearly a year later went on hiatus on The Brainly because of myself as an anxiety and a very stressful year with A.D.H.D., and I really need help from my own schoolwork from my own school about, “A Perimeter Of The Composite Figures” with only 2 more perimeter questions left to go as soon as possible before it’s too late, please! :O
Please read it as soon as possible before answering to 2 of my own perimeter questions and thank you guys. :)
There’s only 55 points for you to answer to my own 2 of my own perimeter questions, guys! :D
Well good luck, guys! :D

Answers
Answer:
2. 26.2 m
3. 117.2 cm
Step-by-step explanation:
You want the perimeters of two figures involving that are a composite of parts of circles and parts of rectangles.
2. Semicircular archThe circumference of a circle is given by ...
C = πd . . . . . where d is the diameter
The length of the semicircle of diameter 12.6 m will be ...
1/2C = 1/2(π)(12.6 m) = 6.3π m ≈ 19.8 m
The two lighted sides of the rectangle have a total length of ...
3.2 m + 3.2 m = 6.4 m
The length of the light string is the sum of these values:
19.8 m + 6.4 m = 26.2 m
The length of the string of lights is about 26.2 meters.
3. Fan shapeThe perimeter of the figure is the sum of four quarter-circles of radius 11.4 cm, and 4 straight edges of length 11.4 cm.
Four quarter-circles total one full circle in length, so we can use the formula for the circumference of a circle:
C = 2πr
C = 2π·(11.4 cm) = 22.8π cm ≈ 71.6 cm
The four straight sides total ...
4 × 11.4 cm = 45.6 cm
The perimeter of the figure is the sum of the lengths of the curved sides and the straight sides:
71.6 cm + 45.6 cm = 117.2 cm
The design has a perimeter of about 117.2 cm.
__
Additional comment
The bottom 12.6 m edge in the figure of problem 2 is part of the perimeter of the shape, but is not included in the length of the light string.
<95141404393>
2.5(4+2/5)=-13 how do I solve this
Answers
Answer: You add 4+2/5 then multiply it times 2.5
Step-by-step explanation:
If you Evaluate it your answer will be: 11 = -13
What is the total volume of snow used to make the snowman if the head is 12 inches wide, the middle is 16 inches wide,and the bottom is 18 inches wide
Answers
Answer:
726.65 cubic inches
Step-by-step explanation:
We are going to assume that the head, middle and bottom are spheres.
The formula to get the volume of a sphere is
\(V= \frac{4}{3}\pi r^{2}\) where r is the radius of the sphere.
Now, let's proceed to apply this formula to the 3 spheres of the snowman:
The head is 12 inches wide (diameter), thus, the radius would be 6 inches:
\(V= \frac{4}{3}\pi r^{2}\\V= \frac{4}{3}\pi 6^{2}\\V= \frac{4}{3}\pi 36\\V=\frac{144\pi }{3} \\V=38\pi\) cubic inches
The middle is 16 inches wide (diameter), thus, the radius would be 8 inches.
\(V= \frac{4}{3}\pi r^{2}\\V= \frac{4}{3}\pi 8^{2}\\V= \frac{4}{3}\pi 64\\V=\frac{256\pi }{3} \\V=85.3\pi\) cubic inches
The bottom is 18 inches wide (diameter), thus the radius would be 9 inches.
\(V= \frac{4}{3}\pi r^{2}\\V= \frac{4}{3}\pi 9^{2}\\V= \frac{4}{3}\pi 81\\V=\frac{324\pi }{3} \\V=108\pi\) cubic inches.
Now, to get the total volume of the snowman we're going to sum up the volume of all three spheres:
Total volume = \(38\pi +85.3\pi +108\pi =231.3\pi\) cubic inches.
If we take pi = 3.1416,
Total volume = \(231.3(3.1416)=726.65\) cubic inches.
2a-6=2(a-3) is their a solution
Answers
Which undefined geometric term is described as a two dimensional set of points.
Answers
The undefined geometric term that is described as a two-dimensional set of points is a "plane."
A plane in geometry is an abstract concept that represents a flat, two-dimensional surface that extends infinitely in all directions. It is a fundamental geometric term that helps us understand and analyze spatial relationships.
When we say that a plane has no thickness, we mean that it is infinitely thin. It does not have any depth or volume. Instead, it is defined by its length and width, which are the dimensions that determine its size and shape.
To visualize a plane, we often use a flat, infinite sheet of paper or a tabletop as a representation. These objects provide a tangible example of a two-dimensional surface that we can observe and work with in the physical world.
To know more about plane,
https://brainly.com/question/4695190
#SPJ11
6 is added to the
product of 7 and a number.
Answers
The equation model of the given statement in question is 6 + 7× x.
What are equation models and arithmetic?The model of equation is defined as the model of the given situation in the form of an equation using constants and variables.
In math, it deals with numbers of operations given according to the statements. The four major arithmetic operators are, addition, subtraction, multiplication, and division.
Given that;
6 is added to product of a number and 7
Now,
Let, the number multiplied by 7 be x,
=7*x
6 is added to the product;
= 6 + 7 × x
Therefore, the equation of model will be given as 6 + 7 × x;
To know more about models visit:
brainly.com/question/22591166
#SPJ9
Explain why each expression is undefined.
csc 180°
Answers
The expression csc 180° is undefined because it corresponds to the cosecant function of 180 degrees. The cosecant function is defined as the reciprocal of the sine function, so csc θ = 1/sin θ.
In trigonometry, the sine function represents the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right triangle. Since the angle in question is 180 degrees, it corresponds to a straight line on the x-axis, where the opposite side has a length of zero. Therefore, the sine of 180 degrees is also zero.
Now, applying the reciprocal operation, we have 1/0, which results in division by zero. Division by zero is undefined in mathematics because it violates the fundamental rules of arithmetic.
In terms of trigonometric functions, division by zero indicates that the function does not have a valid value at that particular angle. In the case of csc 180°, the cosecant function is undefined because it would require dividing by zero.
To summarize, the expression csc 180° is undefined because it involves dividing by zero, which is mathematically invalid and violates the fundamental rules of arithmetic.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
y>=-(7)/(6)x Alot points on the Boundary Ine. Select the Ene to swith between solif and dotted. Select a reglon to shade it.
Answers
The final solution to the inequality y>=-(7)/(6)x is the shaded region on the graph.
To solve the inequality y>=-(7)/(6)x, we will first graph the boundary line and then shade the appropriate region.
1. Begin by graphing the boundary line y=-(7)/(6)x. This line has a slope of -(7)/(6) and passes through the origin (0,0).
2. Since the inequality includes the "greater than or equal to" symbol (>=), the boundary line should be solid to indicate that points on the line are included in the solution.
3. Next, we need to determine which region to shade. To do this, we can choose a test point that is not on the boundary line. A common test point is (0,1), which is above the boundary line.
4. Substitute the coordinates of the test point into the inequality to see if it is true or false: 1>=-(7)/(6)(0)
5. Since the inequality is true, the region that includes the test point is the solution. This means we should shade the region above the boundary line.
6. The final graph should have a solid boundary line with the region above it shaded.
The solution to the inequality y>=-(7)/(6)x is the shaded region on the graph.
To know more about shaded region graph refer here:
https://brainly.com/question/19598687#
#SPJ11
Ruth has already written 21 pages, and she expects to write 2 pages for every additional hour spent writing. How many hours will Ruth have to spend writing this week in order to have written a total of 29 pages? Write and solve an equation to find the answer.
Answers
Answer: 4 hours
Step-by-step explanation:
21+2x=29
29-21=8/2=4 2x/2
Subtract 29-21=8
For 1 hour she writes 2 pages so you
8x2=16
16hrs she spends writing
Find the slope and y-intercept of the line. Graph the line.

Answers
Answer:
Graphing the equation we have;
Explanation:
Given the equation;
\(x+5y=40\)the slope of the line can be derived by expressing the equation in slope-intercept form;
\(\begin{gathered} 5y=-x+40 \\ y=-\frac{1}{5}x+\frac{40}{5} \\ y=-\frac{1}{5}x+8 \end{gathered}\)So, the slope and y-intercept are;
\(\begin{gathered} \text{slope m = -}\frac{1}{5} \\ y-\text{intercept b = 8} \end{gathered}\)to graph the equation, let us find the x-intercept;
\(\begin{gathered} at\text{ y=0;} \\ x+5y=40 \\ x+0=40 \\ x=40 \\ (40,0) \\ at\text{ x=0;} \\ (0,8) \end{gathered}\)Graphing the equation we have;
Other points on the graph includes;
\(\begin{gathered} at\text{ x=10}; \\ y=-\frac{1}{5}(10)+8=-2+8=6 \\ (10,6) \\ at\text{ x=20;} \\ y=-\frac{1}{5}(20)+8=-4+8=4 \\ (20,4) \end{gathered}\)

how to tell if a limit approaches positive or negative infinity
Answers
The approaches of the limits are given as follows:
Negative infinity: graph points down.Positive infinity: graph points up.What is the end behavior of a function?The end behavior of a function refers to how the function behaves as the input variable approaches positive or negative infinity.
Hence, if the function increases indiscriminately, with the graph pointing up, we have that the limits approaches positive infinity, while if the function decreases indiscriminately, with the graph pointing down, we have that the limits approaches negative infinity.
More can be learned about the end behavior of a function at brainly.com/question/1365136
#SPJ4
On a class field trip, there are four buses taking 36 students to the zoo. Each bus has the same number of students. How many students are on each bus?
Answers
Answer: 9 students on each bus
Step-by-step explanation: 36 divied by 4 is 9. There is 9 students on each bus.
PLEASE HELP! ;-;
A particle rotates in a clockwise motion according to the equation x=3cos(0.2t+0.813) what is its frequency?
Answer= [ ? ] hertz
Answers
The particle has a frequency of 0.032 hertz.
The particle experiments a sinusoidal motion, whose mathematical model is described below:
\(x = x_{o} + A\cdot \cos (\omega\cdot t + \phi)\) (1)
Where:
\(x\) - Current position, in meters.\(x_{o}\) - Initial position, in meters. \(\omega\) - Angular frequency, in radians per second. \(t\) - Time, in seconds.\(\phi\) - Angle phase, in radians.The frequency (\(f\)), in hertz is defined by this formula:
\(f = \frac{\omega}{2\pi}\) (2)
By direct observation on the formula described in statement we find that \(\omega = 0.2\,\frac{rad}{s}\), then we find the frequency of the particle by (2):
\(f \approx 0.032\,hz\)
The particle has a frequency of 0.032 hertz.
We kindly invite to check this question on simple harmonic motion: https://brainly.com/question/17315536