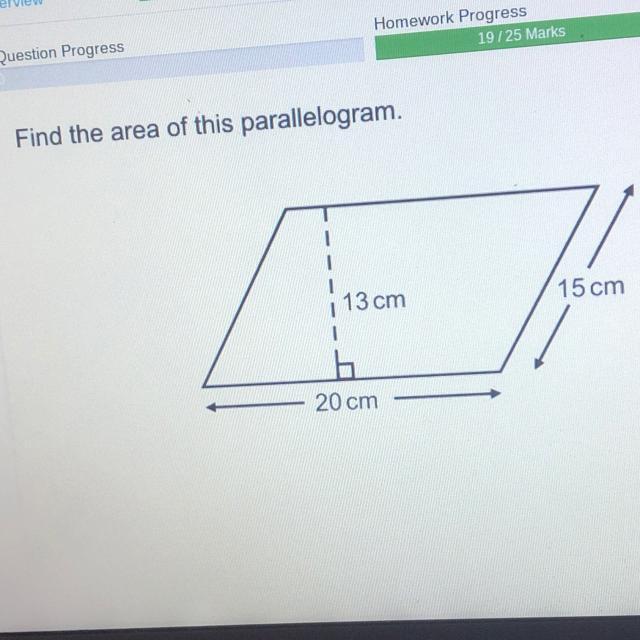
Answers
Answer: 260
Step-by-step explanation: find the base ( which is 20)
Find the height ( which is 13) now A=BxH so
It is 260 :)
Answer:Area+base x perpendicular height
20cm x 13cm
+260cm
Step-by-step explanation:
Related Questions
Plz help thanks I will mark brainliest

Answers
Answer:13x
Step-by-step explanation:I had that
Answer:
I have no clue what a graphical situation is but I do know the answer to x and how to plot it
first of all the answer to x is
x<-3 1/3
So first of all for the graph its a blank circle becuase its not a greater then or equal to sign.
Always iclude 0 in graphs
make a plot out of 1/3 benchmarks
1/2, 2/3, 1, 1 1/3, etc. (but its negative instead)
Now from the -3 1/3 point
make a black circle and make a line pointing to the left
there The graph
-(7) to the power of 4
Which expression shows the power correctly written in expanded
notation?
-7 x -7 x -7 x -7
-7 x 7 x 7 x 7
-4 x -4 x -4 x -4 x -4 x -4 x -4
-4 x 4 x 4 x 4 x 4 x 4 x 4
Answers
Answer:
the first one is correct
Step-by-step explanation:
this is the same way as writing 7 to the power of four, but all of the sevens are negative in your case
Answer:-7x-7x-7x-7
Step-by-step explanation:
in the diagram below chords ab and cd intersect at e if mAEC =4x mAC=120 and mDB = 2x what is the value of x
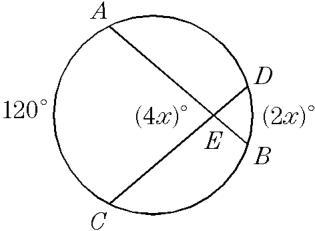
Answers
Answer:
x = 20--------------------------
According to the Angles of Intersecting Chords Theorem, the angle between two chords is half the sum of the intercepted arc measures :
m∠AEC = m∠DEB = (mAC + mDB)/2Substitute and solve for x:
4x = (120 + 2x)/24x = 60 + x3x = 60x = 20A researcher studied the relationship between the number of times a certain species of cricket will chirp in one minute and the temperature outside. Her data is expressed in the scatter plot and line of best fit below. Based on the line of best fit, how many times would the cricket most likely chirp per minute if the temperature outside were 78
F?
Answers
The cricket would most likely chirp 58 times per minute with an outside temperature of 78 ºF.
How to solve the problem?The input and the output of the function graphed in this problem are given as follows:
Input: outside temperature.Output: number of times that the cricket would chirp per minute.One point on the graph is given as follows:
(58,78).
This means that the cricket would most likely chirp 58 times per minute with an outside temperature of 78 ºF.
More can be learned about functions at https://brainly.com/question/1415456
#SPJ1

a given exam has a normal distribution with a mean of 70 and a standard deviation of 10. a sample of size 25 is selected. what percentage of the time would you expect the mean of this sample size to fall below 66?
Answers
Answer:
we would expect the mean of the sample to fall below 66 about 5% of the time
Step-by-step explanation:
To answer this question, we can use the 68-95-99.7 rule, which states that in a normal distribution, approximately 68% of the values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations.
In this case, the mean of the sample is 70 and the standard deviation is 10, so the values that fall within one standard deviation of the mean are between 60 and 80. The values that fall below 66 are outside of this range, so we need to determine what percentage of the values fall within two standard deviations of the mean.
The values that fall within two standard deviations of the mean are between 50 and 90, so the percentage of values that fall below 66 is approximately (100 - 95) = 5%.
Therefore, we would expect the mean of the sample to fall below 66 about 5% of the time.
given that the absolute value of the difference of the two roots of $ax^2 + 5x - 3 = 0$ is $\frac{\sqrt{61}}{3}$, and $a$ is positive, what is the value of $a$?
Answers
The value of "a" is approximately 1.83 given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive.
We are given that the absolute value of the difference between the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive. We need to find the value of "a".
Let the two roots of the equation be r1 and r2, where r1 is not equal to r2. Then, we have:
|r1 - r2| = √(61) / 3
The sum of the roots of the quadratic equation is given by r1 + r2 = -5 / a, and the product of the roots is given by r1 × r2 = -3 / a.
We can express the difference between the roots in terms of the sum and product of the roots as follows:
r1 - r2 = √((r1 + r2)² - 4r1r2)
Substituting the expressions we obtained earlier, we have:
r1 - r2 = √(((-5 / a)²) + (4 × (3 / a)))
Simplifying, we get:
r1 - r2 = √((25 / a²) + (12 / a))
Taking the absolute value of both sides, we get:
|r1 - r2| = √((25 / a²) + (12 / a))
Comparing this with the given expression |r1 - r2| = √(61) / 3, we get:
√((25 / a²) + (12 / a)) = √(61) / 3
Squaring both sides and simplifying, we get:
25 / a² + 12 / a - 61 / 9 = 0
Multiplying both sides by 9a², we get:
225 + 108a - 61a² = 0
Solving this quadratic equation for "a", we get:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61)
Since "a" must be positive, we take the positive root:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61) ≈ 1.83
Therefore, the value of "a" is approximately 1.83.
Learn more about absolute value at
https://brainly.com/question/1301718
#SPJ4
The question is -
Given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive, what is the value of "a"?
what fraction gives a quotient of 2/3 when divided by 1/4
Answers
The fraction that gives a quotient of 2/3 when divided by 1/4 is 8/9.
To find the fraction that gives a quotient of 2/3 when divided by 1/4, we can use the formula:a/b ÷ c/d = ad/bcwhere a/b is the unknown fraction, c/d is the divisor, and 2/3 is the quotient given.The unknown fraction is given by multiplying the divisor and the quotient and putting them in the numerator and denominator, respectively. So, we have:a/b = (c/d) × (2/3)Now, substituting c/d with 1/4, we have:a/b = (1/4) × (2/3)Simplifying, we get:a/b = 2/12 = 1/6Therefore, the fraction that gives a quotient of 2/3 when divided by 1/4 is 1/6.
When a fraction is divided by another fraction, we multiply the dividend with the reciprocal of the divisor. Mathematically, we can write it as:a/b ÷ c/d = a/b × d/cThe multiplication of the dividend with the reciprocal of the divisor gives the unknown fraction. Thus, we have:a/b = (a/b) ÷ (c/d) = (a/b) × (d/c)Now, substituting the given values, we have:x ÷ 1/4 = 2/3Multiplying both sides by 1/4, we get:x = (2/3) × (1/4) = 2/12We can simplify the fraction 2/12 by dividing both the numerator and denominator by 2. So, we get:x = 1/6Therefore, the fraction that gives a quotient of 2/3 when divided by 1/4 is 1/6.
To know more about fraction visit :-
https://brainly.com/question/10354322
#SPJ11
Of all rectangles with a perimeter of 10 meters, which one has the maximum area? (Give both the dimensions and the area enclosed)
Answers
Zone(area) = L x W = 2.5 x 2.5 = 6.25 square meters.
Of all rectangles with an edge of 10 meters, the one that has the greatest zone(area) could be a square.
To see why, let's assume that a rectangle with a border of 10 meters has measurements of length L and width W.
At that point, we know that:
2L + 2W = 10
Rearranging this condition, we get:
L + W = 5
Presently, we need to discover the most extreme range encased by the rectangle, which is given by:
Area = L x W
Able to illuminate for one variable in terms of the other utilizing the condition L + W = 5:
L = 5 - W
Substituting this expression for L into the condition for the zone, we get:
Zone = (5 - W) x W
Extending and disentangling this expression, we get:
Area = 5W - W²
To discover the most extreme esteem of this quadratic expression, we will take its subsidiary with regard to W and set it to break even with zero:
dArea/dW = 5 - 2W =
Tackling for W, we get:
W = 2.5
Substituting this esteem back into the condition for the edge, we get:
L = 2.5
Hence, the measurements of the rectangle that has the greatest region are L = 2.5 meters and W = 2.5 meters, which implies it could be a square. The most extreme zone enclosed by the rectangle is:
Zone(area) = L x W = 2.5 x 2.5 = 6.25 square meters.
To know more about rectangles refer to this :
https://brainly.com/question/2607596
#SPJ4
What do we mean by equidistant?
Answers
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.
In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in n-space is an (n−1)-space.
For a triangle the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to cyclic polygons: the circumcentre is equidistant from each of the vertices. Likewise, the incentre of a triangle or any other tangential polygon is equidistant from the points of tangency of the polygon's sides with the circle.
Learn more about equidistant to visit this link
https://brainly.com/question/29886221
#SPJ4
water is leaking out of an inverted conical tank at a rate of 13100.013100.0 cm3/mincm3/min at the same time that water is being pumped into the tank at a constant rate. the tank has height 15.0 m15.0 m and the the diameter at the top is 3.0 m3.0 m. if the water level is rising at a rate of 20.0 cm/min20.0 cm/min when the height of the water is 3.0 m3.0 m, find the rate at which water is being pumped into the tank in cubic centimeters per minute.
Answers
The rate at which water is being pumped into the tank in cubic centimeters per minute is 289.252.7 \(cm^{3}/min\)
what is volume?the volume that a substance or thing takes up or the space it takes up inside a container, especially when it is large.
given
For the given cone the ratio of radius to height is \(\frac{1}{3}\)
so \(r= \frac{1}{3}h\)
V=\(\pi \frac{r^{2}h}{3}\) becomes V= \(\frac{\pi h^{3} }{27}\)\(\frac{800000}{9}cm^{3}/min\)
\(\frac{dV}{dh}=\frac{\pi h^{2} }{9}\)
We are interested in how Volume has changed over time and see that
\(\frac{dV}{dt}=\frac{dV}{dh} * \frac{dh}{dt}\)
Using the result we already determined for \(\frac{dV}{dh}\) in addition to the given figure of 20 cm/min (at a height of 200 cm )
we get,
\(\frac{dV}{dt } = \frac{\pi (200 cm)^{2}*20 cm }{9 min}\)
= \(\frac{800000}{9}cm^{3}/min\)
or roughly, 279,252.7 \(cm^{3}/min\)
This is the inflow rate necessary to cause an increase in height while ignoring the rate of leakage.
The sum of these two has to represent the actual inflow rate:
279,252.7 \(cm^{3}/min\) + 10000 \(cm^{3}/min\)
289.252.7 \(cm^{3}/min\)
hence the rate at which water is being pumped into the tank in cubic centimeters per minute is 289.252.7 \(cm^{3}/min\)
To know more about volume visit:-
https://brainly.com/question/13338592
#SPJ4
A tennis player ran a simulation twice to estimate the proportion of wins to expect using a new game strategy. Each time, the simulation ran a trial of 1,000 games. The first simulation returned 172 wins, and the second simulation returned 205 wins. Construct and interpret 95% confidence intervals for the outcomes of each simulation.
The confidence interval from the first simulation is (0. 149, 0. 195), and the confidence interval from the second simulation is (0. 180, 0. 230). For the first trial, we are 90% confident the true proportion of wins with the new game strategy is between 0. 149 and 0. 195. For the second trial, we are 90% confident the true proportion of wins with the new game strategy is between 0. 180 and 0. 230.
The confidence interval from the first simulation is (0. 149, 0. 195), and the confidence interval from the second simulation is (0. 180, 0. 230). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0. 149 and 0. 195. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0. 180 and 0. 230.
The confidence interval from the first simulation is (0. 152, 0. 192), and the confidence interval from the second simulation is (0. 184, 0. 226). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0. 152 and 0. 192. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0. 184 and 0. 226.
The confidence interval from the first simulation is (0. 152, 0. 192), and the confidence interval from the second simulation is (0. 184, 0. 226). For the first trial, we are 90% confident the true proportion of wins with the new game strategy is between 0. 152 and 0. 192. For the second trial, we are 90% confident the true proportion of wins with the new game strategy is between 0. 184 and 0. 226
Answers
The correct answer is: The confidence interval from the first simulation is (0. 149, 0. 195), and the confidence interval from the second simulation is (0. 180, 0. 230). For the first trial, we are 95% confident the true proportion of wins with the new game strategy is between 0. 149 and 0. 195. For the second trial, we are 95% confident the true proportion of wins with the new game strategy is between 0. 180 and 0. 230.
What is the confidence interval?The confidence interval is a range of values that is likely to contain the true proportion of wins with the new game strategy based on the sample data.
A 95% confidence interval means that if the simulation is repeated many times, the proportion of wins with the new game strategy will fall within this range 95% of the time.
The correct interpretation of the confidence intervals is that for the first simulation, we are 95% confident that the true proportion of wins with the new game strategy is between 0.149 and 0.195.
This means that if we were to repeat the simulation many times, we would expect the true proportion of wins to fall between these values in 95% of the trials.
Similarly, for the second simulation, we are 95% confident that the true proportion of wins with the new game strategy is between 0.180 and 0.230.
Therefore, the correct answer is an option (b).
To learn more about the confidence interval visit:
https://brainly.com/question/17212516
#SPJ1
what is the range of f?

Answers
Answer:
[-4,5]
Step-by-step explanation:
you look on the starting point and the ending point of the y-axis ( you always start with the smallest value)
f(x)=6+3x
Find the value of f(5)
Answers
Please the inverse of this function!!

Answers
Answer:
\(\frac{5x-3}{4}\)
Step-by-step explanation:
\(x=\frac{4y+3}{5} \\ 5x=4y+3\\ 5x-3=4y\\ \frac{5x-3}{4} =y\)
convert -350 degrees in radians
Answers
Answer:
-(350 degrees) =-(350 degrees) =-6.10865238 radiansAnswer:
-35π/18 radians
Step-by-step explanation:
if you choose two cards out of a deck of cards, what are the chances one is a red face card and the other is a black non-face card?
Answers
Using the probability, if you choose two cards out of a deck of cards, then the chances one is a red face card and the other is a black non-face card is 1/2.
In the given question,
If you choose two cards out of a deck of cards, then we have to find the chances one is a red face card and the other is a black non-face card.
As we know that in a deck having 52 cards. In which 26 are red and 26 are black.
We have to choose a red face card.
As we know that in a deck have 12 face cards. In which 6 red face cards and 6 black face cards.
So the chance of getting red face card is
P(R)=Total number of red face cards/Total number of cards
P(R)=6/52
We have to choose a black non-face card.
We know that in a deck have 6 black face cards and total black cards are 26. So the non face cards are 20.
So the chance of getting black non-face card is
P(B)=Total number of black non-face cards/Total number of cards
P(B)=20/52
Now the chances of getting one is a red face card and the other is a black non-face card is
P(R or B)=P(R)+P(B)
P(R or B)=6/52+20/52
P(R or B)=(6+20)/52
P(R or B)=26/52
P(R or B)=1/2
Hence, if you choose two cards out of a deck of cards, then the chances one is a red face card and the other is a black non-face card is 1/2.
To learn more about probability link is here
brainly.com/question/11034287
#SPJ4
help will reward brainly

Answers
Answer: Positive but I might be wrong I haven't done slopes in a while
Step-by-step explanation:

If it were negative, it would go the opposite way
find the radius of convergence and interval of convergence of the series. sqrt(n)/8^n(x 6)^n
Answers
The interval of convergence is (-2, 14)., the radius of convergence is 8.
To find the radius of convergence, we take half the length of the interval of convergence: Radius of Convergence = (14 - (-2))/2 = 16/2 = 8. Hence, the radius of convergence is 8.
To find the radius of convergence and interval of convergence of the series, we will use the ratio test. Consider the series:
∑ [(√n)/(8^n)] * [(x-6)^n]
Let's apply the ratio test:
lim┬(n→∞)(|(√(n+1))/(8^(n+1)) * ((x-6)^(n+1))| / |(√n)/(8^n) * ((x-6)^n)|)
Simplifying this expression, we get:
lim┬(n→∞)(|√(n+1)/(√n) * ((x-6)/(8))|)
Since we are interested in finding the radius of convergence, we want to find the limit of this expression as n approaches infinity:
lim┬(n→∞)(|√(n+1)/(√n) * ((x-6)/(8))|) = |(x-6)/8| * lim┬(n→∞)(√(n+1)/(√n))
Now, let's evaluate the limit term:
lim┬(n→∞)(√(n+1)/(√n)) = 1
Therefore, the simplified expression becomes:
|(x-6)/8|
For the series to converge, the absolute value of (x-6)/8 must be less than 1. In other words:
|(x-6)/8| < 1
Simplifying this inequality, we have:
-1 < (x-6)/8 < 1
Multiplying each part of the inequality by 8, we get:
-8 < x-6 < 8
Adding 6 to each part of the inequality, we have:
-8 + 6 < x < 8 + 6
Simplifying, we obtain:
-2 < x < 14
Therefore, the interval of convergence is (-2, 14).
Finally, to find the radius of convergence, we take half the length of the interval of convergence:
Radius of Convergence = (14 - (-2))/2 = 16/2 = 8
Hence, the radius of convergence is 8.
Learn more about convergence here:
https://brainly.com/question/31401345
#SPJ11
subtracting decimals
4 - 21
Answers
Answer:
-17
Step-by-step explanation:
It is basically subtracting 4 from 21 except the answer is negative
Which of the following does not represent a function?

Answers
Answer:
D,
Step-by-step explanation:
D would be the only one that doesn't represent a function because the y-value never changes while the x-value does.
Given side AB in triangle ABC has length x, what is the length of side AC?

Answers
The length of the side AC is 2x and this can be determined by using the sine function which is an important trigonometric function.
Given :
Given side AB in triangle ABC has length x.
The trigonometric function can be used to determine the length of the side AC. Sine function can be used to determine the length of AC.
The sine function is the ratio of the opposite side to the hypotenuse. The sine function is given by:
\(\rm sin\theta = \dfrac{Opposite }{Hypotenuse}\)
Now, put the known values in the above equation.
\(\rm sin30^\circ = \dfrac{x}{AC}\)
\(\rm \dfrac{1}{2}=\dfrac{x}{AC}\)
AC = 2x
So, the correct option is D).
For more information, refer to the link given below:
https://brainly.com/question/21286835
Harry invests £6000 in the savings account. The account pays 3.4% compound interests per year. Work out the value of his investment after 3 years. Give your answer to the nearest penny.
Answers
Answer:
£6633.04
Step-by-step explanation:
The formula for compound interest is p(1+r/100)^t
Substitute p with principal, t with time and r with rate
6000(1+3.4/100)^3
6000(103.4/100)^3
6000 x 103.4/100 x 103.4/100 x 103.4/100
Solve to get £6633.04
Help please I am struggling pretty bad thank you

Answers
Answer:
1.024 cm
Step-by-step explanation:
volume of Sphere is given by; V=4/3(πr³).
by making r subject of formula, the equation for r is;
r=³√(3v)/4π
given from question that V=4.5cm³, π=3.14, substituting the values in the equation for r,
we have that;
r=³√[3(4.5)]/[4(3.14)]
r=1.024 cm ( 2 significant figures?
How to add polynomials in brackets
Answers
The innermost parentheses are calculated first, followed by the brackets that form the next layer outwards, followed by braces that form a third layer outwards. Within and outside of parentheses, brackets, and braces, you then follow the normal order of operations as laid out by PEMDAS or other acronyms.
I hope this helps you!!!
What is the difference between midpoint and perpendicular bisector?
Answers
Answer:The midpoint can be any middle part of a line, and the perpendicular Bisector is can only be 90 degrees.
You measure 3 inches between your house and the movie theater. How many miles is in from your house to the movie theater?
Answers
Answer:
4.734 * 10^-5 miles
Step-by-step explanation:
Given that:
Distance between House to movie theater = 3 inches
Expressing the distance in miles :
Converting inch to miles
1 inch = 1.578 * 10^-5 miles
3 inches = (3 * 1.578*10^-5)
3 inches = 4.734 * 10^-5 miles
A graph shows time (minutes) on the horizontal axis and speed (miles per hour) on the vertical axis. Both axes are unnumbered. An orange line is in four sections, labeled A, B, C, D. A starts near the top of the vertical axis and goes down as time increases. B levels out as time continues. C moves up the vertical axis as time continues. D levels out as time continues.
Use the drop-down menus to complete each sentence.
In section A, speed is
as time is increasing.
In section B, speed is
as time is increasing.
In section C, speed is
as time is increasing.
In section D, speed is
as time is increasing.
Answers
Section A shows a decreasing speed, section B and D exhibit a constant speed, and section C displays an increasing speed as time continues. By analyzing the movements of the orange line on the graph.
In section A of the graph, the speed is decreasing as time is increasing. The description mentions that the orange line starts near the top of the vertical axis and goes down as time increases.
This downward movement indicates a decrease in speed. As time progresses, the speed is getting slower, resulting in a negative slope for section A of the graph.
In section B, the speed levels out as time continues. This implies that there is no significant change in speed as time increases. The orange line remains relatively constant, indicating a constant speed. This section is characterized by a horizontal line on the graph.
Moving on to section C, the speed is increasing as time continues. The description mentions that the orange line moves up the vertical axis as time increases. This upward movement signifies an increase in speed. As time progresses, the speed is getting faster, resulting in a positive slope for section C of the graph.
Finally, in section D, the speed levels out as time continues. Similar to section B, there is no significant change in speed as time increases. The orange line remains relatively constant, indicating a constant speed. This section is also characterized by a horizontal line on the graph.
For more such questions on speed
https://brainly.com/question/26046491
#SPJ11
I need some help with this

Answers
Answer:
125
Step-by-step explanation:
Ls señora pepa les dijo a sus hijos Francisco, camila, antonio que saquen cada uno un tercio de caramelos que hay en un frasco Francisco va al frasco y saca su tercio sin contarle a sus hermanos luego va camila y saca su tercio sin decirle a nadie y por último va antonio y saca su tercio. Al final quedan 48 caramelos ¿cuantos caramelos les había comprado la señora pepa
Answers
Answer:
La señora compró 162 caramelos.
Step-by-step explanation:
Sea x la cantidad de caramelos comprada.
Cuando Francisco va al frasco, este toma un tercio de la cantidad total. Es decir \(\frac{x}{3}\). La cantidad restante de caramelos es x-x/3 = \(\frac{2x}{3}\):
Luego, Camila toma un tercio de la cantidad que hay en el frasco, es decir:
\( \frac{2x}{3} \cdot \frac{1}{3}\). Es decir, toma \(\frac{2x}{9}\). La cantidad restante en el frasco es \(\frac{2x}{3}-\frac{2x}{9} = \frac{4x}{9}\).
Finalmente, Antonio toma un tercio de lo que queda, es decir
\( \frac{4x}{9}\cdot \frac{1}{3} = \frac{4x}{27}\).
La cantidad restante en el frasco es
\(\frac{4x}{9}-\frac{4x}{27} = \frac{8x}{27}\).
Finalmente, nos dicen que la cantidad restante es 48.
Es decir,
\(\frac{8x}{27}=48\)
Multiplicando ambos lados de la ecuación por 27/8, tenemos que x = 162.
whats a third of 83 1/2
Answers
Answer:
27.83
The 3 is repeating
Step-by-step explanation: