Answers
Answer:
6√2
Step-by-step explanation:
from the graph the coordinates of the points are (2, 5) and (- 4, -1)
the distance is d= √(x2-x1)²+(y2-y1)² = √(-4-2)²+(-1-5)²=√72 = √2*2*2*3*3= 6√2
Related Questions
If the imple interet on $5000 for 4 year i $1000, then what i the interet rate?
Answers
5% is the interest rate.
What does the term "simple interest" mean?
The principal of a loan or the initial deposit into a savings account serves as the foundation for simple interest. Simple interest does not compound, so the creditor only has to pay interest on the principal sum and the borrower never has to pay interest on the interest that has already accrued.P = $5000
T = 4 Year
S.I. = $1000
R = ?
According to question,
S.I. = P * R* T/100
1000 = 5000 * R * 4/100
R = 1000 * 100/5000 * 4
R = 5%
Learn more about Simple interest
brainly.com/question/25845758
#SPJ4
I also need help on this one too

Answers
Answer:
4x-9= 3x+29
+9 +9
4x=3x+38
-3x -3x
x=38
Now that we have x we can substitute it into one of the equations
3(38)+29=
114+29=
143 <- this is the angle
Answer: x=38
Step-by-step explanation:
(4x-9)=(3x+29)
4x-9=3x+29
combine like terms: subtract 3x from both sides
x-9=29
combine like terms: add 9 to both sides
x=38
Check answer:
4*38=152
152-9=143
3*38=114
114+29=143
which of the following statements must be true about this diagram ? check ALL that apply

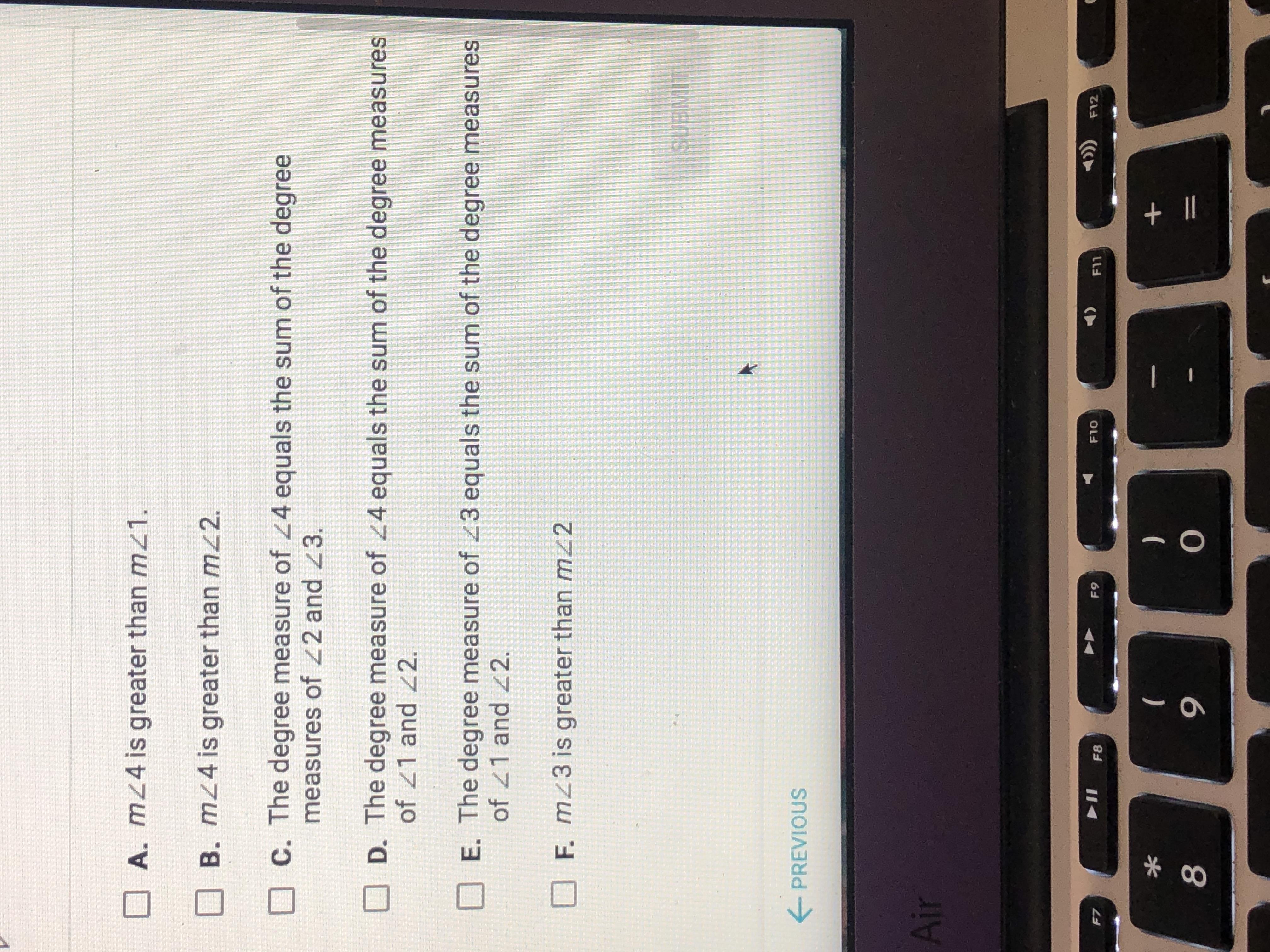
Answers
Answer:
Check A, B and DStep-by-step explanation:
A. m∠4 = 180° - m∠3
m∠1 = 180° - (m∠3 + m∠2)
m∠3 < m∠3 + m∠2 ⇒ m∠4 >m∠1
B. m∠4 = 180° - m∠3
m∠2 = 180° - (m∠3 + m∠1)
m∠3 < m∠3 + m∠1 ⇒ m∠4 >m∠2
C. Not necessarily {could be but not always}
D. m∠4 = 180° - m∠3
m∠1 + m∠2 + m∠3 = 180° ⇒ m∠1 + m∠2 = 180° - m∠3 = m∠4
E. m∠3 = m∠1 + m∠2 only if m∠3 = 90°
F. Not necessarily. {Could be but also could not be. In the picture is, but we don't know if the diagram is accurate or just approximate.}
Select the correct statement:
(this is only briefly mentioned in the video, if you have a difficult time finding it, or just want to make sure you answer is correct, you can find the answer in the book too)
Group of answer choices
Freud is not a stage theorist
Freud is a stage theorist
Answers
Freud is a stage theorist. Sigmund Freud, the renowned Austrian neurologist and psychoanalyst, is widely recognized as one of the pioneers in the field of psychoanalysis.
He proposed a developmental theory that included psychosexual stages of development. According to Freud, human development progresses through distinct stages, each characterized by a specific focus on different erogenous zones. These stages include the oral stage, stage, phallic stage, latency stage, and genital stage. Freud believed that the way individuals navigate these stages influences their personality and psychological well-being in adulthood.
Although Freud's stage theory has been critiqued and modified over time, his ideas regarding the importance of early childhood experiences and unconscious processes have had a profound impact on psychology and continue to shape our understanding of human development.
To know more about psychoanalyst:
https://brainly.com/question/279955
#SPJ4
Select the correct test statistic and critical value.

Answers
Answer:
Step-by-step explanation:
option A
find the measurement of the diagonal if vt=22, then ZT=?

Answers
Answer:
ZT = 11
Step-by-step explanation:
Diagonals of a parallelogram bisects each other.
\( \therefore ZT = \frac {1}{2} \times VT\\\\
\therefore ZT = \frac {1}{2} \times 22\\\\
\therefore ZT = 11\\\\\)
What is an equation of the line
that is perpendicular to the line
y=-x-1
and passes through
the point (-4, 2)?
Answers
Answer:
Step-by-step explanation:
A line that is perpendicular to a reference line will have a slope that is the negative inverse of the reference line.
In this case, the reference line is y = -x - 1. It has a slope of -1. The negative inverse of this would be -(1/-1) = 1.
We can then write:
y = mx + b
y = 1x + b
To find b, enter the one given point that lines on the line, (-4,2).
y = 1x + b
y = 1x + b for (-4,2)
2 = 1(-4) + b
b = 6
The equation becomes y = x + 6
See attached.

Solve |h+3|<5. Write the solution set using set-builder notation.
Answers
Answer:
To solve the inequality |h + 3| < 5, we need to consider two cases, depending on whether the expression inside the absolute value bars is positive or negative:
Case 1: h + 3 >= 0
If h + 3 >= 0, then we can remove the absolute value bars without changing the inequality:
h + 3 < 5
Subtracting 3 from both sides, we get:
h < 2
So the solution for this case is h < 2.
Case 2: h + 3 < 0
If h + 3 < 0, then the inequality becomes:
-(h + 3) < 5
Multiplying both sides by -1 (and reversing the inequality), we get:
h + 3 > -5
Subtracting 3 from both sides, we get:
h > -8
So the solution for this case is h > -8.
Putting these two solutions together, we have:
-8 < h < 2
Therefore, the solution set in set-builder notation is:
{h | -8 < h < 2}
PLEASE HELP IM STUCK ON THIS
which table of values can be defined by the function y=6x-2
x y
-2 10
-1 8
0 6
1 4
2 2
x y
-14 -2
-8 -1
-2 0
4 1
10 2
x y
0 -2
6 -4
12 -6
18 -8
24 -10
x y
-10 -62
-5 -32
0 -2
5 28
10 58
Answers
Answer:
23
Step-by-step explanation:
find the length of segment AB

Answers
Answer:
96
Step-by-step explanation:
Answer:
96
hope this helps you!!
Give the required elements of the hyperbola.
y²/9 - x^2/4=1
The value of a is:
03
04
09
02
Answers
Thus, the value of the y-offset from origin for the given equation of hyperbola y²/9 - x²/4 = 1 is found as: a = 3.
Explain about the hyperbola?This is how a hyperbola looks. Find the values that were utilised to locate the hyperbola's vertices and asymptotes using this form.
(y-k)²/a² - (x-h)²/b² = 1
To make the right side of the equation equal to 1, summarise each term in the equation. The right portion of an equation must equal 1 in order for an ellipse or hyperbola to have the usual shape.
y²/9 - x²/4 = 1
Compare this hyperbola's values to those in the standard form. The variables h and k denote the x and y offsets from the origin, respectively, while 'a' denotes the y-offset.
a = 3
b= 2
k = 0
h = 0
Thus, the value of the y-offset from origin for the given equation of hyperbola y²/9 - x²/4 = 1 is found as: a = 3.
Know more about the hyperbola
https://brainly.com/question/3351710
#SPJ1
find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 5xy. (note: start your answer with y
Answers
The equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is y = (5/2) * x^2y + 1. This equation represents a curve where the y-coordinate is a function of the x-coordinate, satisfying the conditions.
To determine an equation of the curve that satisfies the conditions, we can integrate the slope function with respect to x to obtain the equation of the curve. Let's proceed with the calculations:
We have:
Point: (0, 1)
Slope: 5xy
We can start by integrating the slope function to find the equation of the curve:
∫(dy/dx) dx = ∫(5xy) dx
Integrating both sides:
∫dy = ∫(5xy) dx
Integrating with respect to y on the left side gives us:
y = ∫(5xy) dx
To solve this integral, we treat y as a constant and integrate with respect to x:
y = 5∫(xy) dx
Using the power rule of integration, where the integral of x^n dx is (1/(n+1)) * x^(n+1), we integrate x with respect to x and get:
y = 5 * (1/2) * x^2y + C
Applying the initial condition (0, 1), we substitute x = 0 and y = 1 into the equation to find the value of the constant C:
1 = 5 * (1/2) * (0)^2 * 1 + C
1 = C
Therefore, the equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is:
y = 5 * (1/2) * x^2y + 1
Simplifying further, we have:
y = (5/2) * x^2y + 1
To know more about equation of the curve refer here:
https://brainly.com/question/31467851#
#SPJ11
Is it true that If A is a 3×3 matrix, then det5A = 5detA.
Answers
Yes, it is true that if A is a 3×3 matrix and K is a scalar, then det(KA) = \(K^3\) det(A).
To see why this is true, let's use the definition of the determinant of a matrix. For a 3×3 matrix A with entries\(ka_{11}, ka_{12}, ka_{13}, ka_{21}, ka_{22}, ka_{23}, ka_{31}, ka_{32}, ka_{33}\), the determinant det(A) is given by:
\(det(A) = a11(a22a33 - a23a32) - a12(a21a33 - a23a31) + a13(a21a32 - a22a31)\)
Now consider the matrix KA, where K is a scalar. The entries of KA are simply the entries of A multiplied by K. In other words, the entries of KA are:
\(ka_{11}, ka_{12}, ka_{13}, ka_{21}, ka_{22}, ka_{23}, ka_{31}, ka_{32}, ka_{33}\)
Using the same formula as above, we can calculate the determinant of KA:
\(det(KA) = (K a_{11})(K a_{22})(K a_{33}) - (K a_{11})(K a_{23})(K a_{32}) - (K a_{12})(K a_{21})(K a_{33})+ (K a_{12})(K a_{23})(K a_{31}) + (K a_{13})(K a_{21})(K a_{32}) - (K a_{13})(K a_{22})(K a_{31)\)
Substituting in the entries of KA, we get:
\(det(KA) = (K a_{11})(K a_{22})(K a_{33}) - (K a_{11})(K a_{23})(K a_{32}) - (K a_{12})(K a_{21})(K a_{33})+ (K a_{12})(K a_{23})(K a_{31}) + (K a_{13})(K a_{21})(K a_{32}) - (K a_{13})(K a_{22})(K a_{31)\)
Simplifying this expression, we get:
\(det(KA) = K^3 (a_{11} a_{22}a_{33} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31})\)
But this is just the same as\(K^3\) times the determinant of A! Therefore, we have shown that det(KA) =\(K^3\)det(A) for any 3×3 matrix A and scalar K.
for such more question on matrix
https://brainly.com/question/31043586
#SPJ11
Question
Is it true that If A is a 3×3 matrix, then det (KA) = K^3 * det(A)
is -14/2 a real number
Answers
Answer:
yes
Step-by-step explanation:
yes it will still be a real number
because real numbers are both rational and irrational
-14/2=-7
therefore -7 is also a real number
answer- it depends because -14/2 could be represented as a fraction and if that is the case it is a real number. but this could also be shown as a division equation.
Step-by-step explanation:
Find the generating function of the sequence {an}n≥0 determined by an = an−1 + 6an−1 with initial conditions a0 = 1, a1 = 3. You need to find the closed form of the generating function, but you don’t need find the closed form of the coefficients.
Answers
The generating function for the sequence {an} is given by a(x) = (1 + 2x) / (1 - x - 6x^2). It captures the terms of the sequence {an} as coefficients of the powers of x.
To find the generating function of the sequence {an}, we can use the properties of generating functions and solve the given recurrence relation.
The given recurrence relation is: an = an-1 + 6an-2
We are also given the initial conditions: a0 = 1 and a1 = 3.
To find the generating function, we define the generating function A(x) as:
a(x) = a0 + a1x + a2x² + a3x³ + ...
Multiplying the recurrence relation by x^n and summing over all values of n, we get:
∑(an × xⁿ) = ∑(an-1 × xⁿ) + 6∑(an-2 × xⁿ)
Now, let's express each summation in terms of the generating function a(x):
a(x) - a0 - a1x = x(A(x) - a0) + 6x²ᵃ⁽ˣ⁾
Simplifying and rearranging the terms, we have:
a(x)(1 - x - 6x²) = a0 + (a1 - a0)x
Using the given initial conditions, we have:
a(x)(1 - x - 6x²) = 1 + 2x
Now, we can solve for A(x) by dividing both sides by (1 - x - 6x^2²):
a(x) = (1 + 2x) / (1 - x - 6x²)
Therefore, the generating function for the given sequence is a(x) = (1 + 2x) / (1 - x - 6x²).
Read more on Functions here: https://brainly.com/question/29890699
#SPJ11
A person must score in the upper 2% of the population on an IQ test to qualify for membership in Mensa, the international high IQ society. If IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. what score must a person have to qualify for Mensa? If required, round your answers to nearest whole number.£
Answers
Answer:
130.81
Step-by-step explanation:
Given that :
Mean, μ = 100
Standard deviation, σ = 15
To obtain the upper 2% of scores :
We find the Zscore (value) of the upper 2% from the normal probability distribution table ;
Zscore corresponding to the area in the left of (1 - 0.02) = 2.054
Using this with the Zscore formula :
Zscore = (x - μ) / σ
2.054 = (x - 100) / 15
2.054 * 15 = x - 100
30.81 = x - 100
30.81 + 100 = x
x = 130.81
An administrator of a TANF program is concerned about the length of time hard-to-place clients were able to gain employment. He wants to contrast the average length of time at a job for his clients with the national average. What statistic should he use
Answers
The administrator should use the mean duration of employment for his clients to compare it with the national average. This will help determine if his hard-to-place clients have shorter or longer job durations than the average.
What statistic should be used to compare the job duration of TANF program clients with the national average?To contrast the average length of time at a job for his clients with the national average, the administrator of the TANF program should use the mean duration of employment for his clients and compare it to the national average.
This would provide a measure of the central tendency of employment durations for his clients and allow him to compare this measure to the corresponding national statistic.
However, it is important to note that this measure alone may not provide a complete picture of employment outcomes for hard-to-place clients in the TANF program.
The administrator may also want to consider other statistical measures such as the median duration of employment or the standard deviation to get a better understanding of the distribution of employment durations among his clients.
The median duration of employment would provide a measure of the middle value of employment durations, which may be a more representative statistic if there are outliers or extreme values in the data.
The standard deviation would provide a measure of the variability in employment durations among his clients, which would be useful in determining whether there is a wide range of outcomes or if most clients have similar employment durations.
In addition to statistical measures, the administrator may also want to consider qualitative factors such as the types of jobs his clients are able to secure and whether they are able to advance in their careers over time.
This would provide a more nuanced understanding of employment outcomes and allow for a more comprehensive evaluation of the effectiveness of the TANF program in supporting hard-to-place clients in gaining and maintaining employment.
Learn more about administrator statistic
brainly.com/question/28218199
#SPJ11
8.1 + u/7 = -3.1
Please help, Thanks!!
Answers
Alternative Form
4=-782/5,u=-78.4
Help me pls I don’t know what it is

Answers
The bread recipe calls for 2 more cups of flour per cup of sugar than the cookie recipe.
========================================================
Explanation:
I'll use this shorthand
s = sugarf = flourSomething like "2 cups of sugar" will shorten to "2s".
The cookies need 3s for every 6f.
Therefore we get this ratio
3s : 6f
And we can divide both sides by 3 to end up with
s : 2f
Meaning "each cup of sugar needs 2 cups of flour".
--------------------
Meanwhile, the bread recipe calls for 2s for every 8f.
2s : 8f
2s/2 : 8f/2 .... divide both sides by 2
s : 4f
When making bread, each cup of sugar needs 4 cups of flour. In other words, the amount of flour is quadruple that of the sugar.
--------------------
Recap
Cookies have the ratio of s : 2fBread has the ratio of s : 4fThese ratios are reduced so that we have "s" on the left side without any numbers attached to it. In other words, we have 1s.
We can see that the bread needs 2 more cups of flour compared to the cookies (since 4f - 2f = 2f). It's important that we reduce those ratios so that we're talking about the same amount of sugar for each food item.
This is why choice B is the final answer.
--------------------
An example:
Each food item will use 1 cup of sugar.
The cookies need twice the amount of flour, so the cookies require 2 cups of flour (because of the ratio s:2f mentioned earlier).
The bread needs quadruple the amount of flour compared to sugar. Meaning the bread needs 4 cups of flour (because of the ratio s:4f).
Then subtract to get
(4 cups flour for bread) - (2 cups flour for cookies) = 2 cups flour
if f(x)=5x-6 determine the value of x if f(x) = 44
Answers
Given:-
\(f(x)=5x-6\)To find the value when f(x) is 44.
So now we substitute the value and simplify to find the value of x. so we get,
\(\begin{gathered} f(x)=5x-6 \\ 44=5x-6 \\ 5x=44+6 \\ 5x=50 \\ x=10 \end{gathered}\)So the value of x is 10.
Which lines have a slope of -2?

Answers
Answer:
Lines C and D
Step-by-step explanation:
Both lines C and D are negative, and they both have the same slope. in order to find the slope you use rise over run; in this case, you go down 2 over left 1. C and D are the only lines that use that slope; therefore, they are the answers.
Evaluate 64½
with steps please
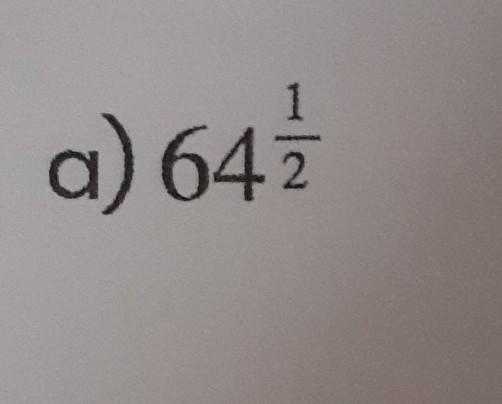
Answers
Answer:
8
Step-by-step explanation:
64¹⁺² = √64 = √8 * 8
= 8
Answer:
\(8\)
Step-by-step explanation:
\( {64}^{ \frac{1}{2} } \\ {2}^{6 \times \frac{1}{2} } \\ {2}^{ \frac{6}{2} } \\ {2}^{3} \\ 2 \times 2 \times 2 \\ 4 \times 2 \\ = 8\)
Hope this helps you.
Let me know if you have any other questions :-):-)
In a family with 7 children, excluding multiple births, what is the probability of having 7 boys? Assume that a girl is as likely as a boy at each birth. Let E be the event that the family has 7 boys, where the sample space S is the set of all possible permutations of girls and boys for 7 children. Find the number of elements in event E, n(E), and the total number of outcomes in the sample space, n(S). n(E) = n(S)=
Answers
The probability of having 7 boys in a family with 7 children is 1 out of 128, as there is only one favorable outcome out of 128 total possible outcomes.
To find the probability, we need to calculate n(E) and n(S).
In this case, event E represents the scenario where all 7 children are boys. The sample space S consists of all possible permutations of boys and girls for the 7 children, which is 2^7 = 128.
This is because each child has 2 possibilities (boy or girl), and we multiply these possibilities for all 7 children.
Since event E includes only one specific outcome (all boys), n(E) is equal to 1. Therefore, both n(E) and n(S) are 1 and 128, respectively. The probability of having 7 boys is given by n(E)/n(S) = 1/128.
Learn more about Probability click here : brainly.com/question/30034780
#SPJ11
Can someone turn this into y=ax+b form with your work?

Answers
Step-by-step explanation:
given
2x + y = 13
turning to y = ax + b we get
y = - 2x + 13
hope it helps :)❤
given the following all-integer linear program: max 15x1 2x2 s. t. 7x1 x2 < 23 3x1 - x2 < 5 x1, x2 > 0 and integer a. solve the problem as an lp, ignoring the integer constraints. b. what solution is obtained by rounding up fractions greater than or equal to 1/2? is this the optimal integer solution? c. what solution is obtained by rounding down all fractions? is this the optimal integer solution? explain. d. show that the optimal objective function value for the ilp (integer linear programming) is lower than that for the optimal lp. e. why is the optimal objective function value for the ilp problem always less than or equal to the corresponding lp's optimal objective function value? when would they be equal? comment on the optimal objective function of the milp (mixed-integer linear programming) compared to the corresponding lp and ilp.
Answers
The required solution of the linear programming problem for the given objective function and subject to constraints are,
Linear programming problem is Maximize 15x1 + 2x2
Subject to:
7x1 + x2 < 23
3x1 - x2 < 5
x1, x2 > 0
Objective function value for rounding up fraction 1/2 solution is 53
Objective function value for rounding up all fraction solution is 23.
Optimal objective function value 53 is lower than optimal value 95.5.
Optimal objective function value is always less than or equal to the LP's optimal objective function value as ILP problem is a more constrained version.
To solve the problem as an LP,
we can ignore the integer constraints
And solve the problem as a continuous linear program.
The problem can be written as,
Maximize 15x1 + 2x2
Subject to:
7x1 + x2 < 23
3x1 - x2 < 5
x1, x2 > 0
Rounding up fractions greater than or equal to 1/2,
The following feasible solution is,
x1 = 3, x2 = 4
The objective function value for this solution is 53.
However, this is not the optimal integer solution since both x1 and x2 are not integers.
Rounding down all fractions, we get the following feasible solution,
x1 = 1, x2 = 4
The objective function value for this solution is 23, which is less than the LP's optimal objective function value of 95.5.
This is not the optimal integer solution either.
Optimal objective function value for the ILP is lower than that for the optimal LP, solve the ILP problem.
In any one constraints
When x1 = 0 ⇒ x2 = 23
x2 = 0 ⇒ x1 = 3.3
Optimal value is ,
15(3.3) + 2(23)
= 49.5 + 46
= 95.5
Optimal objective function value is lower than optimal value.
The optimal objective function value for the ILP problem is always less than or equal to the corresponding LP's optimal objective function value .
Because the ILP problem is a more constrained version of the linear programming problem.
The ILP problem restricts the variables to be integers, which reduces the feasible region and makes the problem more difficult to solve.
The optimal objective function values for the LP and ILP problems are equal.
If the LP problem has an optimal solution that satisfies the integer constraints.
In general, the optimal objective function value of the MILP problem can be better or worse than that of the LP or ILP problem.
It depends on the specific problem instance.
learn more about linear programming here
brainly.com/question/28443444
#SPJ4
The above question is incomplete, the complete question is :
Given the following all-integer linear program:
Max 15x1 + 2x2
s. t.
7x1 + x2 < 23
3x1 - x2 < 5
x1, x2 > 0 and integer
a. solve the problem as an lp, ignoring the integer constraints.
b. what solution is obtained by rounding up fractions greater than or equal to 1/2? is this the optimal integer solution?
c. what solution is obtained by rounding down all fractions? is this the optimal integer solution? explain.
d. show that the optimal objective function value for the ilp (integer linear programming) is lower than that for the optimal lp.
e. why is the optimal objective function value for the ilp problem always less than or equal to the corresponding lp's optimal objective function value? when would they be equal? comment on the optimal objective function of the milp (mixed-integer linear programming) compared to the corresponding lp and ilp.
Quick! I need an answer now! Please!
Linear or nonlinear:
y=x y=x/2 - 3 3x + y =12 y= 6/x - 2 y=3x^3+5
Answers
this equation is a non linear equation
In this case, many of the equations, such as Y=x/2-3 have no exponents, which means they are linear
The only one that is nonlinear is the last one, which has an x^3. This graph would look wiggly (as to mean non linear)
The measure of an angle is 19.5°. What is the measure of its complementary angle?
Answers
Answer:
70.5
In Maths, two angles are said to be complementary, when the angles add up to 90 degrees. The complementary angle need not be adjacent to each other, but its sum should be equal to 90 degrees. For example, 47° and 43° are complementary angles.
Example:
To find out another angle if one of the complementary angles is 60°
Solution:
We know that the sum of complementary angles is 90
Let the unknown angle be x
Thus,
60° + x = 90°
X = 90° – 60°
X = 30°
Hence, the unknown angle is 30°
NEED ANSWER ASAP : The formula gives the maximum height y of a projectile launched straight up, given acceleration a and initial velocity v.
y=v^2/2a
Solve for v.
Responses
v=2ay√/a
v equals fraction numerator square root of 2 a y end root over denominator a end fraction
v=4a^2y^2
v equals 4 a squared y squared
v=4y^2/a^2
v equals fraction numerator 4 y squared over denominator a squared end fraction
v=2ay−−−√
Answers
The required expression is v = √2ay.
Let acceleration is given by: a
and initial velocity is given by: v
So, The maximum height(y) is
y= v² sinθ / 2a
As, θ=90 then
y = v² /2a
v² = 2ay
v = √2ay
Thus, the required expression is v = √2ay.
Learn more about Expression here:
https://brainly.com/question/9584905
#SPJ1
Enter equivalent equation
8x + 3 = 1x – 10
Answers
Exact form:
x= - 13/3
Decimal form:
x= -1.857142
Mixed number form:
x=- 1 6/7
Liz is buying a home for $426,000. She is making a 22% down payment and financing the rest with a 20-year loan at 5.25% interest.
What will her total payment for the home be? Round your answer to the nearest dollar.
Use a mortgage table to find the monthly mortgage payment per 1000 dollars borrowed.
$598,424
$600,306
$610,442
$631,057

Answers
In linear equation, $869,776 will her total payment for the home be .
What in mathematics is a linear equation?
An algebraic equation with simply a constant and a first-order (linear) term, such as y=mx+b, where m is the slope and b is the y-intercept, is known as a linear equation.
Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.
You have to use the number in the intersection of the row for 5.25% interest and the column for 20 years.
The number is $6.74.
That means that, for every $1,000 borrowed for 20 years at 5.25% interest you will pay $6.74 every month.
2. Amount borrowed
You will make a 22% down payment:
Thus the amount borrowed is $426,000 - $93,720 = $332,280
3. Monthly payment
Multiply the monthly payment per 1,000 by the amount borrowed divided by 1,000:
4. Total monthly payments:
Multiply the number of payments by the monthly payment.
Number of payments = 20 years × 12 payments /year = 240 payments.
5. Total payment for the home.
The total payment for the home will be the down payment plus the amount paid to the bank:
$322,280 + $537,496 = $869,776
Learn more about a linear equation.
brainly.com/question/29739212
#SPJ1
