Find the image of (-9, 4) for a dilation centered at the origin with a scale factor of 3/4.
Answers
Point A = (0, 0)
Point B = (-9, 4)
Scale factor = 3/4
Dilation point (-6.75 , 3)
Related Questions
Select all instances in which the variable described is binomial.
a. A coin flip has two outcomes: heads or tails. The probability of each outcome is 0.50. The random variable represents the total number of flips required to get tails.
b. A quality check on a particular product must meet five guidelines. All products are made in the same factory under the same conditions. The random variable represents the total number of products out of 35 tested that pass inspection.
c. Based on the parents' genetics, each of 6 children from a particular pair of parents has a 0.30 probability of having blue eyes. The random variable represents the total number of children from this pair of parents with blue eyes.
d. There are two banking options for customers of ABC Bank, checking or savings. The random variable represents the total number out of 567 customers with a checking account.
e. The probability of drawing an ace in a standard deck of cards is 0.08. Seven cards are drawn without replacement. The random variable represents the total number of ace cards observed.
Answers
Answer: a. , c. , d., e.
Step-by-step explanation:
A variable that counts how many times a certain event occurs in a particular number of trials is known as binomial random variable.
For each trial, there exist only two outcomes .
The probability of for each event is the same on each trial.
a. Event has two outcomes with same probability as 0.50, therefore the random variable represents the total number of flips required to get tails is a binomial random variable.
b. Total guidelines are 5.
Here total outcomes are not 2 , it does not meet with the conditions of binomial.
c. The random variable represents the total number of children from this pair of parents with blue eyes has two outcomes (where has or not.)
also, the probability of having blue eyes is same in each trial, so it represents binomial random variable.
d. The random variable represents the total number out of 567 customers with a checking account has two outcomes (checking or savings).
So, it represents binomial random variable.
e. The random variable represents the total number of ace cards observed has two outcomes ( ace or not ace).
So it represents the binomial random variable.
What is the size of the reflex angle below to the nearest degree? PLSSSSS

Answers
The size of the reflex angle above to the nearest degree is 277 degrees.
What is a circle?In Mathematics, a circle can be defined as a closed, two-dimensional curved geometric shape with no edges or corners. Additionally, a circle refers to the set of all points in a plane that are located at a fixed distance (radius) from a fixed point (central axis) with a measure of 360 degrees.
What is a reflex angle?A reflex angle can be defined as a type of angle that is more than 180 degrees but less than 360 degrees.
Based on the information provided about this circle (protractor), we have:
83 + x = 360
x = 360 - 83
x = 277 degrees.
Read more on reflex angle here: https://brainly.com/question/30195819
#SPJ1
Please help with work, thank you in advanced!

Answers
Answer:
ans is
\( \frac{9}{8x {}^{6} y {}^{3} } \)
Solve the equation. k − 34 = 71
Answers
Answer:
105
Step-by-step explanation:
\(k − 34 = 71 \\ \\ k = 71 + 34 \\ \\ k = 105\)
Answer:
k=105
Step-by-step explanation:
34+71=105
if f(1) =2 and f(n)= f(n-1)-3 find the value of f(5)
Answers
Answer:
f(5) = -10
Step-by-step explanation:
Let's go through the calculation step by step to find the value of f(5) using the given recursive formula f(n) = f(n-1) - 3.
Start with the initial value f(1) = 2, as given in the problem.
To find f(2), we use the recursive formula f(n) = f(n-1) - 3. Since n = 2, we have f(2) = f(1) - 3. Plugging in the value of f(1) as 2, we get f(2) = 2 - 3 = -1.
Continuing the pattern, we find f(3) = f(2) - 3 = -1 - 3 = -4. We subtract 3 from the previous term f(2) to obtain f(3).
Moving on, f(4) = f(3) - 3 = -4 - 3 = -7. Again, we subtract 3 from the previous term f(3) to calculate f(4).
Finally, f(5) = f(4) - 3 = -7 - 3 = -10. Following the recursive formula, we subtract 3 from the previous term f(4) to determine f(5).
Therefore, the value of f(5) is -10.
Hope this helps!
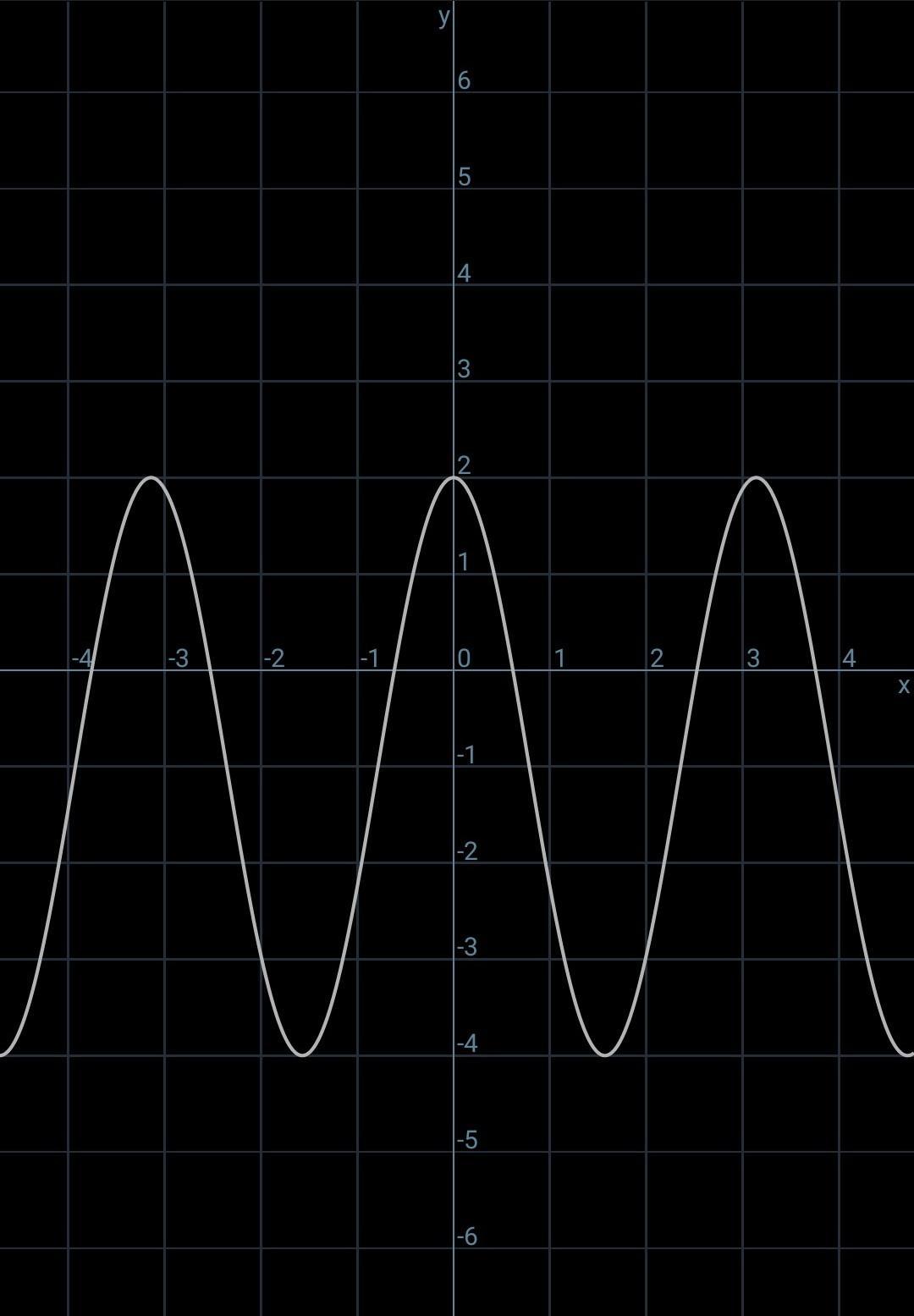
Graph h(x)=3cos(2x)−1.
Use 3.14 for π.

Answers
Step-by-step explanation:
the answer is in the attachment
Answer:
The right answer is in yellow.
Step-by-step explanation:
Took the quiz :)

In one jar, I have two balls labelled 1 and 2 respectively. In a second jar, I have three balls labelled 0, 1 and 2 respectively. I draw one ball from each jar, multiply the numbers on the two balls together, and then calculate three to the power of that product, e.g. if I draw 1 and 2, I calculate 3^2=9. Let’s call this number X. What is the probability that the number 1,024 is an exact multiple of X?
Answers
Step-by-step explanation:
this is a kind of trick question, actually.
with whatever we draw, we produce X values as power of 3.
to be precise, we can have only
3⁰ = 1
3¹ = 3
3² = 9
3⁴ = 81
due to the possible combinations of drawn numbers (e.g. 3 cannot be created by a multiplication of 0s, 1s and 2s).
so, mostly, these results cannot be exact factors of 1024.
1024 cannot be divided by 3, nor by 9 nor by 81.
but 1024 is a multiple of 1 (as is every number).
so, we are looking at the probability to get 0 as multiplication result of the numbers on the 2 drawn balls.
the only possibilities are
1 and 0
2 and 0
out of in total 6 (2×3) different outcomes
1 and 0
1 and 1
1 and 2
2 and 0
2 and 1
2 and 2
the probability of this "0" event is again
number of desired outcomes / number of possible outcomes = 2/6 = 1/3
Assume that a population is normally distributed with a mean of 100 and a standard deviation of 15. Would it be unusual for the mean of a sample of 3 to be 115 or more? Why or why not?
Answers
Answer:
|Z| < 2, which means that it would not be unusual for the mean of a sample of 3 to be 115 or more.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
If \(|Z| > 2\), the value of X is considered to be unusual.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Assume that a population is normally distributed with a mean of 100 and a standard deviation of 15.
This means that \(\mu = 100, \sigma = 15\)
Sample of 3
This means that \(n = 3, s = \frac{15}{\sqrt{3}}\)
Would it be unusual for the mean of a sample of 3 to be 115 or more? Why or why not?
We have to find the z-score.
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{115 - 100}{\frac{15}{\sqrt{3}}}\)
\(Z = 1.73\)
|Z| < 2, which means that it would not be unusual for the mean of a sample of 3 to be 115 or more.
Fill in the box below to write an expression that is equivalent to:
7 (2x + y)
8x + 2y + 9x + 5y -
Answers
17x+7y
Or 31x+14y
The Bear Lake in Idaho is 24 miles long. Suppose John starts cycling at one end at 20 mph and Ramona starts at the other end at 16 mph. How long would it take them to meet?
A. 30 min
B. 35 min
C. 40 min
D. 45 min
E. 50 min
Answers
Answer:
30 mins
Step-by-step explanation:
20 / 16 is 1.25 then multiply 24 miles by 1.25 and you get 30 mins
I need help with this math problem.

Answers
Answer:
Answer and steps in picture.

What is the simplified value of the expression below? One-third divided by two-thirds 0 One-third One-half 1
Answers
Answer:
It is one half 1
2
Step-by-step explanation:
did test on edg 2020
Answer:
c on edge 2021
Step-by-step explanation:
1/2
A laboratory manager was interested in buying a new pipette. Company A was selling 2 pipettes for £300 less than Company B was selling 3 pipettes for. For a single pipette, Company A was more expensive by £60 than Company B.
Answers
The price of the pipette for company A and company B will be $480 and $420, respectively.
What is the solution to the equation?The allocation of weights to the important variables that produce the calculation's optimum is referred to as a direct consequence.
A research facility supervisor was keen on purchasing another pipette. Organization A was selling 2 pipettes for £300 not as much as Organization B was selling 3 pipettes for. For a solitary pipette, Organization A was more costly by £60 than Organization B.
Let 'x' be the price of the pipette of company A and 'y' be the price of the pipette of company B. Then the equations are given as,
2x = 3y - 300 ...1
x = y + 60 ...2
From equations 1 and 2, then we have
2(y + 60) = 3y - 300
2y + 120 = 3y - 300
y = 420
Then the value of x is given as,
x = 420 + 60
x = 480
The price of the pipette for company A and company B will be $480 and $420, respectively.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ1
What is the mean of this data?
12, 9, 4, 10, 15
Enter your answer in the box.
Answers
Step-by-step explanation:
the mean is always the sum of all data divided by the number of data points.
we have 5 data points.
their sum is
12 + 9 + 4 + 10 + 15 = 50
the mean is
50/5 = 10
Please help with this!!

Answers
Answer:
2x + 4
Step-by-step explanation:
So sorry if this is wrong, I'm rusty in this area of math
Shyla answered 38 out of 40 questions correctly on the quiz. What percent did she answer correctly? She answered 95% correctly. Show the proportion and work that gives that answer.
Answers
Answer: I think 90 %
Step-by-step explanation:
Answer:
it is 95%
Step-by-step explanation:
Calculate, correct to one decimal plice
the acute angle between the lines
3x - 4y + 5 = 0 and 2x + 3y -1 = 0
A. 70.69
B. 50.2
C. 39.8
D. 19.4
Answers
Answer:
A. 70.69 is the correct answer.
Step-by-step explanation:
Given:
Two lines:
\(3x - 4y + 5 = 0 \\2x + 3y -1 = 0\)
To find:
Angle between the two lines = ?
Solution:
Acute Angle between two lines can be found by using the below formula:
\(tan \theta = |\dfrac{(m_1 - m_2)}{ (1 + m_1m_2)}|\)
Where \(\theta\) is the acute angle between two lines.
\(m_1, m_2\) are the slopes of two lines.
Slope of a line represented by \(ax+by+c=0\) is given as:
\(m = -\dfrac{a}{b }\)
So,
\(m_1 = -\dfrac{3}{- 4} = \dfrac{3}{4}\)
\(m_2 = -\dfrac{2}{ 3}\)
Putting the values in the formula:
\(tan \theta = |\dfrac{(\dfrac{3}{4}- (-\dfrac{2}{3}))}{ (1 + \dfrac{3}{4}\times (-\dfrac{2}{3 }))}|\\\Rightarrow tan \theta = |\dfrac{\dfrac{3}{4}+\dfrac{2}{3}}{ (1 -\dfrac{1}{2})}|\\\Rightarrow tan \theta = |\dfrac{\dfrac{17}{12}}{ \dfrac{1}{2}}|\\\Rightarrow tan \theta = \dfrac{17}{6}\\\Rightarrow \theta = tan^{-1}(\frac{17}{6})\\\Rightarrow \theta = \bold{70.69^\circ}\)
So, correct answer is A. 70.69
Read 3 integer numbers from the user; these numbers represent the lengths of 3 straight lines. From the 3 lengths, determine whether a triangle can be formed with the corresponding lines. If it is possible to form a triangle, determine whether the triangle is a right triangle or not. The rules to be used are: 1. To form a triangle where all lines’ ends meet (form vertices), the sum of the lengths of two sides must be greater than the length of the third side. This short video illustrates this concept: How to determine if the three sides make up a triangle. 2. Per the Pythagorean theorem: in a straight triangle, the square of the length of the longest side (the hypotenuse) is equal to the sum of the squares of the lengths of the other two sides. 3. The user can enter the lengths of each line in any order, i.e.: you may not assume that the first length is the longest or the smallest or the middle value.
Answers
Answer:
Written in Python
print("Enter three sides of a triangle: ")
length = []
for i in range(0,3):
inp = int(input(""))
length.append(inp)
length.sort()
if length[1]+length[2] > length[0] and length[0] + length[2] > length[1] and length[0] + length[1] > length[2]:
print("Triangle")
if length[2]**2 == length[0]**2 + length[1] **2:
print("Right Angled")
else:
print("Not Right Angled")
else:
print("Not Triangle")
Step-by-step explanation:
This line prompts user for sides of triangle
print("Enter three sides of a triangle: ")
This line declares an empty list
length = []
The following iteration gets user input
for i in range(0,3):
inp = int(input(""))
length.append(inp)
This line sorts user input
length.sort()
The following if condition checks if user input is triangle
if length[1]+length[2] > length[0] and length[0] + length[2] > length[1] and length[0] + length[1] > length[2]:
The following is executed is the if condition is true
print("Triangle")
The following if condition checks if user input forms a right angled triangle
if length[2]**2 == length[0]**2 + length[1] **2:
print("Right Angled")
else:
print("Not Right Angled")
This is executed if user input is not a triangle
else:
print("Not Triangle")
A certain type of car has room for 4 passengers.
Using the equation you made on question 6. Solve for how many cars would be needed to fit 78 passengers?
Answers
Solve for x .
5+ln(x-4)=4
Do not round any intermediate computations, and round your answer to the nearest hundredth.
Answers
The value of x = 4.3679
Now, According to the question:
Let's Know:
A logarithm (or log) is the mathematical expression used to answer the question: How many times must one “base” number be multiplied by itself to get some other particular number? For instance, how many times must a base of 10 be multiplied by itself to get 1,000? The answer is 3 (1,000 = 10 × 10 × 10).
Given the data is:
5+ln(x-4) = 4
ln(x-4) = 4 - 5
In (x - 4) = -1
x - 4 = \(e^-^1\)
x = \(e^-^1\) + 4
x = 0.3679 + 4
x = 4.3679
Learn more about Logarithm at:
https://brainly.com/question/27389970
#SPJ4
Let t be the number of weeks Dr. Elder is on his diet and D(t) be a linear equation that models his weight in pounds. At the beginning of his diet, t=0, Dr. Elder weighs 265 pounds, D(0)=265. After nine weeks, t=9, he now weighs 229 pounds, D(9)=229. Find the slope
Answers
Using it's concept, it is found that the slope of the function is of -4.
What is the slope of a function?The slope of a function is given by the change in the output of the function divided by the change in the input.
For this problem, in 9 months, his weight changed from 265 pounds to 229 pounds, hence it changed -36 pounds, which means that the slope is of:
m = -36/9 = -4.
More can be learned about the slope of a function at https://brainly.com/question/24808124
#SPJ1
A mountain is 13,318 ft above sea level and the valley is 390 ft below sea level What is the difference in elevation between the mountain and the valley
Answers
Answer: 13,708 ft
Step-by-step explanation:
To find the difference in elevation between the mountain and the valley, we need to subtract the elevation of the valley from the elevation of the mountain:
13,318 ft (mountain) - (-390 ft) (valley) = 13,318 ft + 390 ft = 13,708 ft
Therefore, the difference in elevation between the mountain and the valley is 13,708 ft.
Answer: The difference is 13,708 ft.
Given that a mountain is 13,318 feet above sea level. So the elevation of the mountain is \(= +13,318 \ \text{ft}\).
Given that a valley is 390 feet below sea level.
So the elevation of the valley is \(= -390 \ \text{ft}\).
So the difference between them is \(= 13,318 - (-390) = 13,318 + 390 = 13,708 \ \text{ft}.\)
Learn more: https://brainly.com/question/20521181
Please help if you know how to do this, thanks




Answers
9514 1404 393
Answer:
1. see the first attachment for a graph; quadrants I, II, III; vertex (-3, -4); x-intercepts -5, -1; graph is dashed line, shaded inside the parabola, which opens up
2. see the second attachment for a graph; all quadrants; vertex (1, 2); x-intercepts 1±√2; graph is a solid line, shaded outside the parabola, which opens down; (-7, 0) is a solution
Step-by-step explanation:
1. The boundary expression is in vertex form, so the vertex can be read directly.
y = (x -h)^2 +k . . . . . . parabola with vertex (h, k)
y > (x +3)^2 -4 . . . . . (h, k) = (-3, -4)
The leading coefficient is +1, a positive number, so the parabola opens up. The relation is y > ( ), so values of y above the dashed line will be shaded. Those values are inside the parabola. The points (0, 0) and (-7, 0) are not in the shaded area, so are not solutions.
__
2. Again, the boundary expression is in vertex form, so the vertex can be read directly.
y ≥ -(x -1)^2 +2 . . . . . (h, k) = (1, 2)
The x-intercepts are found by solving for x when y=0:
0 = -(x -1)^2 +2
x -1 = ±√2
x = 1±√2
The leading coefficient is -1, so the parabola opens downward. The relation is y ≥ ( ), so y-values above the solid line will be shaded. Those values are outside the parabola. Point (0, 0) is not a solution. Point (-7, 0) is a solution.
_____
Additional comment
As with the graph of any inequality, the boundary line is solid when the "or equal to" case is part of the relation. If the relation is strictly "greater than" or "less than", then the boundary line is dashed.


b) In a certain weight lifting machine, a weight of 1 kN is lifted by an effort of 25 N. While the weight moves up by 100 mm, the point of application of effort moves by 8 m. Find mechanical advantage, velocity ratio and efficiency of the machine
Answers
The mechanical advantage of the given machine is 40, Velocity ratio is 80 and efficiency is 0.5.
The given question is concerned with finding the mechanical advantage, velocity ratio and efficiency of a weight lifting machine.
The problem has provided the following information:
Weight of the object, W = 1 kN = 1000 NEffort applied, E = 25 NHeight through which the object is lifted, h = 100 mm = 0.1 m Distance through which the effort is applied, d = 8 m
We know that, mechanical advantage = load/effort = W/E and velocity ratio = distance moved by effort/distance moved by the load.Mechanical advantage
The mechanical advantage of the given machine is given by; Mechanical advantage = load/effort = W/E= 1000/25= 40Velocity ratioThe velocity ratio of the given machine is given by;
Velocity ratio = distance moved by effort/distance moved by the load.= d/h = 8/0.1= 80EfficiencyThe efficiency of the given machine is given by;
Efficiency = (load × distance moved by load) / (effort × distance moved by effort)Efficiency = (W × h) / (E × d)= (1000 × 0.1) / (25 × 8)= 0.5
Therefore, the mechanical advantage of the given machine is 40, velocity ratio is 80 and efficiency is 0.5.
For more questions on Velocity .
https://brainly.com/question/25749514
#SPJ8
a 90% confidence interval is found to be (72,78). what is the margin of error
Answers
The margin of error for the 90% confidence interval is 3.
To find the margin of error for a 90% confidence interval, we can use the formula:
Margin of Error = (Upper Limit - Lower Limit) / 2
Given the confidence interval (72, 78), where 72 is the lower limit and 78 is the upper limit, we can substitute these values into the formula to calculate the margin of error.
Margin of Error = (78 - 72) / 2
Margin of Error = 6 / 2
Margin of Error = 3
Consequently, the 90% confidence interval's margin of error is 3.
for such more question on margin of error
https://brainly.com/question/10218601
#SPJ8
Perform the indicated operation.
2w + 16w
p^3 x p^5
7k - 3k
5z x z^3
Answers
Answer:
18w
p^8
4k
5z^4
Step-by-step explanation:
1. 2w+ 16w= 18w
2. when multiplying exponents just add the exponents giving you p^8
3. 7k - 3k= 4k
4. 5z also equals 5z^1 and just like problem two you will just add the exponents but you will leave the coefficient( 5 alone) giving you 5^4
Alternate exterior angles are congruent which angle forms a pair of alternate exterior angles with angle 2?

Answers
An account manager for a local software firm believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: Salesperson Number of Contacts Sales (in millions) 1 14 24 2 12 14 3 20 28 What is the dependent variable
Answers
Answer:
Amount of sales
Step-by-step explanation:
The dependent variable also called the measured or predicted variable is simply the variable obtained due to inputs in of the independent variable. It is the variable which is being measured in an experiment. Here, the test is that the number of sales depends on the number of contact. Here, the number of contacts will has an influence or determines the amount of sales, hence, the number of contacts is the independent variable while the amount of sales is the dependent variable.
The multiplicative inverse of -2¹/₇ is
Answers
The multiplicative inverse of a number is the reciprocal of that number. Since
-2 1/7 *(-7/15)= 1, then -7/15 is the multiplicative inverse of -2 1/7.
Which ordered pair is a solution to the following linear system? y = x y = –x
Answers
Answer:
(2,2) (-1,-1)
Step-by-step explanation
i think this is there answer im sorry if im wrong