find the lcm of the following numbers by division method.
198 and 352
with process
Answers
Answer:
198 = 2 × 3² × 11
352 = 2⁵ × 11
LCM = (2 × 11) × 3² × 2⁴ = 5544
Therefore, the LCM of 198 and 352 using the division method is 5544.
Related Questions
What is the value of x in the equation - - *?
0 32
18
18
0 32

Answers
Answer:
x= 18
Step-by-step explanation:
How large should we choose n so that the trapezoid-rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001? (Use the error bound given in Section 5.9 of the course text.)
Answers
The trapezoidal rule is a numerical integration method that uses trapezoids to estimate the area under a curve. The trapezoidal rule can be used for both definite and indefinite integrals. The trapezoidal rule approximation, Tn, to the integral sin r dz is given by:
Tn = (b-a)/2n[f(a) + 2f(a+h) + 2f(a+2h) + ... + 2f(b-h) + f(b)]where h = (b-a)/n. To determine how large n should be so that Tn is accurate to within 0.00001, we can use the error bound given in Section 5.9 of the course text. According to the error bound, the error, E, in the trapezoidal rule approximation is given by:E ≤ ((b-a)³/12n²)max|f''(x)|where f''(x) is the second derivative of f(x). For the integral sin r dz, the second derivative is f''(r) = -sin r. Since the absolute value of sin r is less than or equal to 1, we have:max|f''(r)| = 1.
Substituting this value into the error bound equation gives:E ≤ ((b-a)³/12n²)So we want to choose n so that E ≤ 0.00001. Substituting E and the given values into the inequality gives:((b-a)³/12n²) ≤ 0.00001Simplifying this expression gives:n² ≥ ((b-a)³/(0.00001)(12))n² ≥ (b-a)³/0.00012n ≥ √(b-a)³/0.00012Now we just need to substitute the values of a and b into this expression. Since we don't know the upper limit of integration, we can use the fact that sin r is bounded by -1 and 1 to get an upper bound for the integral.
For example, we could use the interval [0, pi/2], which contains one full period of sin r. Then we have:a = 0b = pi/2Plugging in these values gives:n ≥ √(pi/2)³/0.00012n ≥ 5073.31Since n must be an integer, we round up to the nearest integer to get:n = 5074Therefore, we should choose n to be 5074 so that the trapezoidal rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001.
To know more about integration visit :
https://brainly.com/question/31744185
#SPJ11
Solve the inequality -5x<20. Write the solution set in inte
Answers
The solution set for the inequality -5x < 20, expressed as an interval, is (-∞, -4).
To solve the inequality -5x < 20, we need to isolate the variable x. First, we divide both sides of the inequality by -5, remembering to flip the direction of the inequality sign when dividing by a negative number. This gives us x > -4.
The solution set can be expressed as an interval notation, which indicates all the values that satisfy the inequality. In this case, since x is greater than -4, the solution set is (-∞, -4), where -∞ represents negative infinity and the parentheses indicate that -4 is not included in the solution set.
Therefore, the solution set for the inequality -5x < 20, in interval notation, is (-∞, -4).
Learn more about solving inequalities here: brainly.com/question/21857626
#SPJ11
If sint=18 , and t is in quadrant i, find the exact value of sin(2t) , cos(2t) , and tan(2t) algebraically without solving for t
Answers
The value of Sin2t is 1/4 and cos2t is (15/16)^1/2 and tan2t is 1/(15)^1/2.
According to the statement
we have given that the sint=1/8 then we have to find the exact value of
sin(2t) , cos(2t) , and tan(2t).
Here the value of Sint = 18
then sin2t becomes
sin2t = 2*1/8 then
sin2t = 1/4.
And
(Cos2t)^2 = 1 - (Sin2t)^2
(Cos2t)^2 = 1 - 1/16
(Cos2t)^2 = (16 - 1)/16
(Cos2t)^2 = 15/16
(Cos2t) = (15/16)^1/2
then
tan2t = sin2t/cos2t
tan2t = (1/4)/(15)^1/2 / 4
tan2t = 1/(15)^1/2
these are the values of given terms.
So, The value of Sin2t is 1/4 and cos2t is (15/16)^1/2 and tan2t is 1/(15)^1/2.
Learn more about TRIGONOMETRY here https://brainly.com/question/13276558
#SPJ4
on the island of mumble, the mumblian alphabet has only $5$ letters, and every word in the mumblian language has no more than $3$ letters in it. how many words are possible? (a word can use a letter more than once, but $0$ letters does not count as a wor
Answers
The total number of possible words is 155.
How many words are possible? (A word can use a letter more than once, but 0 letters do not count as a word)
There are 5 letters in the mumblian alphabet, and each word must contain 1, 2, or 3 letters.
The number of 1 letter words is 5 since every letter is a word.
The number of 2 letter words is 5 × 5 = 25 because there are 5 options for the first letter and 5 options for the second letter.
The number of 3 letter words is 5 × 5 × 5 = 125 because there are 5 options for the first letter, 5 options for the second letter, and 5 options for the third letter. Therefore, the total number of possible words is:
\($5 + 25 + 125 = \boxed{155}$\)
To know more about letter words problems: https://brainly.com/question/29424977
#SPJ11
What must added to 4 3/5 to make seven?
Answers
Answer:
the answer would be 2 and 2/5
Step-by-step explanation:
3/5 + 2/5 = 1
and, 4 + 2 = 6
6 + 1 = 7
hope this helps :)
Answer:
\(2 \frac{2}{5} \)
Step-by-step explanation:
To find the answer we subtract four and three fifths from 7
\(7 - 4\frac{3}{5} = \frac{7}{1} - \frac{23}{5} \)
when subtracted we get
\(2 \frac{2}{5} \)
What is the solution to this equation?
2x - x + 9 + 3x - 2 = 16
O A - 23
B. x - 3
O O O o
c. x-?
D. . -
Answers
Answer:
the answer is b
Step-by-step explanation:
Answer:
x = 9/4
Step-by-step explanation:
2x - x + 9 + 3x - 2 = 16
Combine like terms
4x + 7 = 16
Subtract 7 from both sides
4x = 9
Divide both sides by 4
x = 9/4
it is not necessary to have a base case in all recursive algorithms true or false
Answers
False. It is necessary to have a base case in all recursive algorithms.
A base case is a condition that stops the recursion process and returns a result. Every recursive algorithm must have a base case. The base case is the point at which the recursion will stop, and the function will begin to return the values from the call stack. The base case is necessary to stop the recursive algorithm from entering an infinite loop that will cause it to consume all available resources, resulting in a stack overflow error. If there is no base case, the algorithm will continue to call itself until the stack overflows, which will result in a runtime error.
In conclusion, a base case is essential in all recursive algorithms, and the lack of one can result in a stack overflow error.
To know more about recursive algorithms visit:
brainly.com/question/32999356
#SPJ11
what is the length of the line? the first quadrant of an x- y- coordinate plane. a line segment extends from two, eight to twelve, two.
Answers
The length of the line segment is approximately 12.04 units. This formula calculates the distance between two points, (x1, y1) and (x2, y2), on the line segment. The formula is as follows: d = √((x2 - x1)^2 + (y2 - y1)^2)
The length of a line segment in a two-dimensional x-y coordinate plane can be found using the distance formula. This formula calculates the distance between two points, (x1, y1) and (x2, y2), on the line segment. The formula is as follows:
d = √((x2 - x1)^2 + (y2 - y1)^2)
In this case, the line segment extends from the point (2, 8) to the point (12, 2). By plugging these values into the formula, we find that:
d = √((12 - 2)^2 + (2 - 8)^2) = √(100 + 36) = √136 = 12.04
So, the length of the line segment is approximately 12.04 units. This formula is useful for finding the distance between any two points in a two-dimensional plane and can be used in various fields such as geometry, physics, and engineering. The formula is based on the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
Learn more about coordinates here: brainly.com/question/16634867
#SPJ4
Complete question:
What is the length of the line segment in the first quadrant of an x-y coordinate plane that extends from (2, 8) to (12, 2)?
Answer:
its D 136
Step-by-step explanation:
khan
H E L P P L S S S S S S S ! ! !

Answers
Answer:
i would be a reflection so the 2nd option
Answer:
That is a reflection
Step-by-step explanation:
That is an example of a reflection because the image is reflected over the line :)
A quantity with an initial value of 3600 grows continuously at a rate of 2.5% per decade. What is the value of the quantity after 47 years, to the nearest hundredth
Answers
The value of the quantity after 47 years is approximately 4071.38.
To find the value of the quantity after 47 years, we'll use the formula for continuous compound growth:
Final Value = Initial Value * (1 + Growth Rate) ^ Time
Here, Initial Value = 3600, Growth Rate = 2.5% (which is 0.025 as a decimal), and Time = 47 years.
However, the growth rate is given per decade. So, first, we need to convert the time into decades:
Time (in decades) = 47 years / 10 years/decade = 4.7 decades
Now, we can use the formula:
Final Value = 3600 * (1 + 0.025) ^ 4.7
Final Value ≈ 3600 * (1.025) ^ 4.7
Final Value ≈ 3600 * 1.130939
Now, rounding the final value to the nearest hundredth:
Final Value ≈ 4071.38
So, the value of the quantity after 47 years is approximately 4071.38.
to learn more about continuous compound growth click here:
brainly.com/question/1601228
#SPJ11
What is the slope of the line through (-4,2)(−4,2)left parenthesis, minus, 4, comma, 2, right parenthesis and (3,-3)(3,−3)left parenthesis, 3, comma, minus, 3, right parenthesis?
Answers
Answer:
The slope of the line through the points is -5/7
Step-by-step explanation:
Here, we want to calculate the value of the slope through the lines
Mathematically;
m = y2-y1/(x2-x1)
Where (x1,y1) = (-4,2)
and (x2,y2) = (3,-3)
Substituting these values, we have;
m = (-3-2)/(3-(-4)) = -5/7 = -5/7
The slope of the line through (-4, 2) and (3, -3) is; -5/7
According to the question;
We are required to determine the slope of the line through the points given.The slope, m of the line is given mathematically as;
m = (y2 -y1)/(x2 - x1)Therefore, in this case;
Slope, m = (-3 - 2)/(3 -(-4))Slope, m = -5/7
Read more:
https://brainly.com/question/16949303
Asx approaches negative infinity, for which of the following functions does f(x) approach positive infinity? Select all that apply. Select all that apply: f(x) =2x5 Ofx)9x +100 f(x)= 6x8 +9x6+32 f(x)=-8x3 + 11 f(x)=-10x +5x+ 26 f(x)=-x +8x4 + 248
Answers
Among the provided functions, the ones that approach positive infinity as x approaches negative infinity are:
- f(x) = 2x^5
- f(x) = 6x^8 + 9x^6 + 32
- f(x) = -x + 8x^4 + 248
To determine which functions approach positive infinity as x approaches negative infinity, we need to analyze the leading terms of the functions. The leading term dominates the behavior of the function as x becomes very large or very small.
Let's examine each function and identify their leading terms:
1. f(x) = 2x^5
The leading term is 2x^5, which has a positive coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and positive, indicating that f(x) approaches positive infinity.
2. f(x) = 9x + 100
The leading term is 9x, which has a positive coefficient but a lower power of x compared to the constant term 100.
As x approaches negative infinity, the leading term becomes very large and negative, indicating that f(x) approaches negative infinity, not positive infinity.
3. f(x) = 6x^8 + 9x^6 + 32
The leading term is 6x^8, which has a positive coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and positive, indicating that f(x) approaches positive infinity.
4. f(x) = -8x^3 + 11
The leading term is -8x^3, which has a negative coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and negative, indicating that f(x) approaches negative infinity, not positive infinity.
5. f(x) = -10x + 5x + 26
Combining like terms, we have f(x) = -5x + 26.
The leading term is -5x, which has a negative coefficient but a lower power of x compared to the constant term 26.
As x approaches negative infinity, the leading term becomes very large and positive, indicating that f(x) approaches negative infinity, not positive infinity.
6. f(x) = -x + 8x^4 + 248
The leading term is 8x^4, which has a positive coefficient and the highest power of x.
As x approaches negative infinity, this term becomes very large and positive, indicating that f(x) approaches positive infinity.
Therefore, the correct choices are:
- f(x) = 2x^5
- f(x) = 6x^8 + 9x^6 + 32
- f(x) = -x + 8x^4 + 248
To know more about functions refer here:
https://brainly.com/question/28134738#
#SPJ11
If the volume of a cube shaped box is 795 cubic inches, which equation would you uses to determine how many 1-inch cubes could fit along one side.
Pls help ASAP

Answers
1.1. How many m³ = are there in 3( mile )³
1.2. How many gal/min correspond to 5ft³ /s. 1.3. Convert the following: 9.50 cm to nm/sec² (5)
Answers
Using the conversion factors, we find that 3 cubic miles is approximately equal to 1.2504543 × 10^10 cubic meters. 5 cubic feet per second is equal to 2244.156 gallons per minute. 9.50 centimeters is equal to 9.50 * 10^7 nanometers per second squared.
1.1. One mile is equal to 1609.34 meters. Since we're dealing with cubic units, we cube the conversion factor.
1 mile = 1609.34 meters
1 mile³ = (1609.34 meters)³ = 4.168181 × 10^9 cubic meters
Therefore, 3 cubic miles is equal to 3 * 4.168181 × 10^9 cubic meters, which is approximately 1.2504543 × 10^10 cubic meters.
1.2. To convert from cubic feet per second (ft³/s) to gallons per minute (gal/min), we use the appropriate conversion factors.
Here are the conversion factors:
1 cubic foot = 7.48052 gallons
1 minute = 60 seconds
So, we set up the conversion as follows:
5 ft³/s * 7.48052 gal/ft³ * 60 s/min = 2244.156 gal/min
Therefore, 5 cubic feet per second is equal to 2244.156 gallons per minute.
1.3. To convert centimeters (cm) to nanometers per second squared (nm/sec²), we use the appropriate conversion factors. Here are the conversion factors:
1 centimeter = 10^7 nanometers
1 second = 1 second
So, we set up the conversion as follows:
9.50 cm * (10^7 nm/cm) / (1 sec)² = 9.50 * 10^7 nm/sec²
Therefore, 9.50 centimeters is equal to 9.50 * 10^7 nanometers per second squared.
To know more about conversion factors, refer to the link :
https://brainly.com/question/30567263#
#SPJ11
My book have 120 Pagés if i have read half of it how Many Pagés I have read
Answers
Answer:
60..........
.........
Answer:
60
Step-by-step explanation:
120/2
60
You have read 60 pages
if the bug can come crawl at a rate of 0.107 VUUNITS/seconds, how long would it take the bug to travel from corner A to corner B



Answers
Given :
The dimensions of the Box
Length = 23.5 , Width = 24 , Height = 31.5
Task 1 :
The distance from A to B =
\(\sqrt[]{23.5^2+24^2+31.5^2}=\sqrt[]{2120.5}=46.05\)The bug fly at a rate of 0.519 Vunits/sec
So, the time of flying = distance/speed = 46.05/0.519 = 88.73 seconds
Task 2 :
The distance from A to B = 46.05 VUNITS
The bug crawl at a rate of 0.107 VUNITS/sec
So, the time of crawling = 46.05/0.107 = 430.36 seconds
Callie drew the map below to show her
neighborhood.
School
y
654321
-6-5-4-3-2-10
346
Grocery--4
Store -5
Library
Park
1 2 3 4 5 6
Hospital.
Fire
Station
X
If each unit in the coordinate plane
represents 1.5 miles, how many miles.
is it from the school to the grocery store?
Answers
Based on the information, it is 3 miles from the school to the grocery store.
How to calculate tie distanceLooking at the map, we can see that the school is located at (-4, 5) and the grocery store is located at (-5, 4). The horizontal distance between them is 1 unit, and the vertical distance is also 1 unit.
Therefore, the total distance between the school and the grocery store is:
Distance = (horizontal distance) x (distance per unit) + (vertical distance) x (distance per unit)
Distance = 1 x 1.5 miles + 1 x 1.5 miles
Distance = 3 miles
Learn more about Distance on
https://brainly.com/question/26550516
#SPJ1
Cronbach's alpha indicates to what extent scale items are correlated to each other?
True
False
Answers
False. Cronbach's alpha is a measure of internal consistency reliability, not a measure of the correlation between scale items.
It assesses the extent to which the items in a scale or questionnaire are measuring the same underlying construct.
Cronbach's alpha is calculated based on the inter-item correlations among the items in a scale. It provides a measure of the average correlation between all possible pairs of items in the scale. The range of Cronbach's alpha is between 0 and 1, with higher values indicating greater internal consistency or reliability.
Essentially, Cronbach's alpha quantifies the extent to which the items in a scale are consistently measuring the same construct or concept. It assesses how well the items "hang together" as a reliable measurement tool.
While correlation between scale items is related to internal consistency, Cronbach's alpha specifically measures the degree to which the items are interrelated and provides a single coefficient that reflects the overall reliability of the scale. It does not directly indicate the extent of item-item correlations or the strength of individual item contributions to the scale.
Learn more about questionnaire at: brainly.com/question/27972710
#SPJ11
please help me this assignment is already late

Answers
The degree of polynomial 4x ^2 y+x^ 2 -2y ^2 is
Answers
Answer:
degree 3
Step-by-step explanation:
The degree of a polynomial is determined by the largest exponent of the term within the polynomial.
4x²y = 4x²\(y^{1}\) ← with exponent 2 + 1 = 3
x² ← exponent 2
- 2y² ← exponent 2
The term with the largest exponent is 4x²y with exponent 3
Then the polynomial is of degree 3
SOMEONE PLZ HELP ME!!!!!

Answers
Answer:
5 m/s
Step-by-step explanation:
cos 60 = 300/x
x = 300/cos 60 = 600
600m / 120sec
5 m/s
The manager of a mechanic shop notices that Julio can change a tire in 5 minutes while his twin brother Jaden takes 10 minutes. How much time would it take both brothers working simultaneously to change one tire if Julio only works 2 minutes
Answers
According to the given work and time, if Julio works for only 2 minutes, it would take approximately 3.33 minutes for both Julio and Jaden working together to change one tire.
Julio can change a tire in 5 minutes, while his twin brother Jaden takes 10 minutes. We need to determine how much time it would take for both brothers, working simultaneously, to change one tire if Julio only works for 2 minutes.
Let's assume that the time it takes for both brothers working together to change one tire is represented by "t" minutes. We can set up a proportion based on the work rates of Julio and Jaden:
Julio's work rate: 1 tire / 5 minutes
Jaden's work rate: 1 tire / 10 minutes
Combined work rate: 1 tire / t minutes
According to the work rate principle, the combined work rate is the sum of the individual work rates. Therefore, we have the equation:
1/5 + 1/10 = 1/t
To find the value of "t", we need to solve this equation. Multiplying through by the least common denominator (LCD) of 10t, we get:
2t + t = 10
Combining like terms, we have:
3t = 10
Dividing both sides by 3, we find:
t = 10/3
So, it would take both Julio and Jaden working simultaneously approximately 3.33 minutes (or 3 minutes and 20 seconds) to change one tire if Julio only works for 2 minutes.
Therefore, if Julio works for only 2 minutes, it would take approximately 3.33 minutes for both Julio and Jaden working together to change one tire.
Learn more about Work and Time here:
brainly.com/question/19382734
#SPJ11
How many students are enrolled in a course either in calculus, discrete mathematics, data structures, 7. or programming languages at a school if there are 507, 292, 312, and 344 students in these courses, respectively; 14 in both calculus and data structures; 213 in both calculus and programming languages; 211 in both discrete mathematics 558 and data structures; 43 in both discrete mathematics and programming languages; and no student may take calculus and discrete mathematics, or data structures and programming languages, concurrently
Answers
Answer:
974
Step-by-step explanation:
Let assume that:
The set of student that took part in Calculus be = C
Those that took part in discrete mathematics be = D
Let those that took part in data structures be = DS; &
Those that took part in Programming language be = P
Thus;
{C} = 507
{D} = 292
{DS} = 312
{P} = 344
For intersections:
{C ∩ DS} = 14
{C ∩ P} = 213
{D ∩ DS} = 211
{D ∩ P} =43
{C ∩ D} = 0
{DS ∩ P} = 0
{C ∩ D ∩ DS ∩ P} = 0
According to principle of inclusion-exclusion;
{C ∪ D ∪ DS ∪ P} = {C} + {D} + {DS} + {P} - {C ∩ D} - {C ∩ DS} - {C ∩ P} - {D ∩ DS} - {D ∩ P} - {DS ∩ P}
{C ∪ D ∪ DS ∪ P} = 507 + 292 + 312 + 344 - 14 - 213 - 211 - 43 - 0
{C ∪ D ∪ DS ∪ P} = 974
Hence, the no of students that took part in either course = 974
Please help and provide an explanation for why the answer is f(x) = 3/2x + 7
What is the equation of the line that passes through Point (-4, 1) and has a Slope of 3/2.
Answers
Answer:
see below
Step-by-step explanation:
the point-slope equation is
y-1 = 3/2 (x+4)
Answer:
\(y=\frac{3}{2}x+7\)
Step-by-step explanation:
To write the equation of a line, two information are needed.
Slope (also known as gradient)A pair of coordinates (or a point) on the lineThe slope can be calculated using the gradient formula as long as two pairs of coordinates are given. This question provides the slope, hence we can substitute its value into the equation right away.
In slope-intercept form, the equation of a line is given by y= mx +c, where m is the slope and c is the y-intercept. The slope gives us the steepness of the line, while the y-intercept is the y value in which the line cuts through the y-axis (vertical axis).
y= mx +c
Given that slope= \(\frac{3}{2}\), m= \(\frac{3}{2}\).
Substitute the value of m:
\(y=\frac{3}{2}x+c\)
Next, find the value of c by substituting a pair of coordinates.
When x= -4, y= 1,
\(1=\frac{3}{2} (-4)+c\)
1= -6 +c
Add 6 to both sides:
c= 1 +6
c= 7
Substituting the value of c:
\(\bf{y=\frac{3}{2}x +7 }\)
For more examples on writing equation of lines, check out: https://brainly.com/question/27941697
help me with this answer please
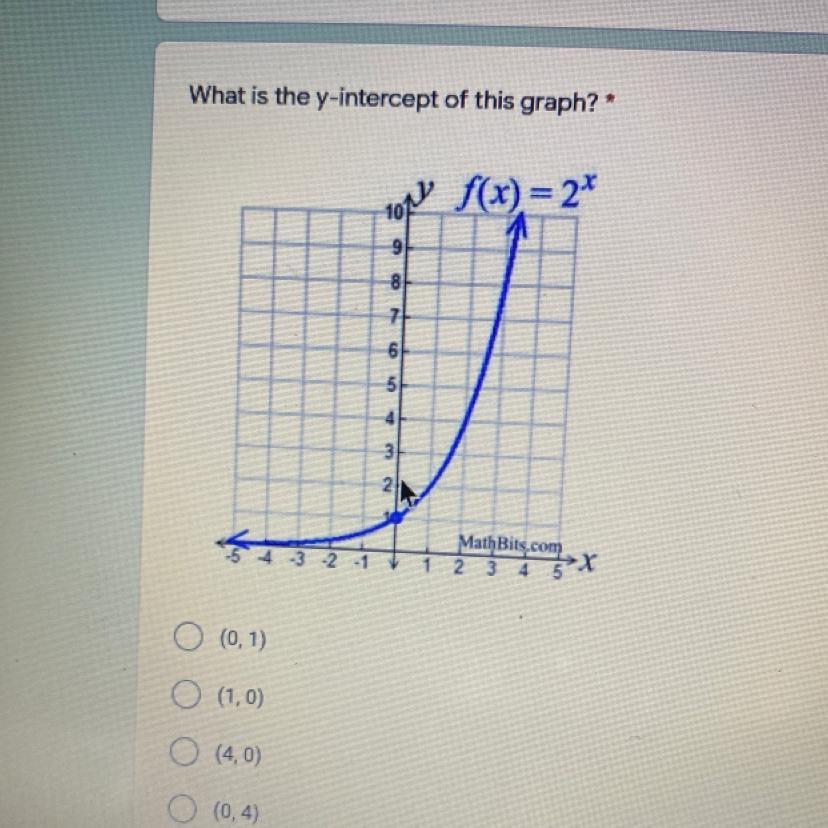
Answers
Answer:
(0,1)
Step-by-step explanation:
0 because its intercept at 0 x-axis
1 because its intercept at 1 y-axis
also it is written in this way (0,1) because we write first the number on x-axis then y-axis
Can you simply these fractions?

Answers
Answer:
2/7
3/4
1/2
1/10
5/7
3/8
1/9
2/5
1/5
Step-by-step explanation:
I'm a junior lol
Answer:
10/35= 2/7
18/24= 3/4
10/15= 2/3
3/6= 1/2
3/30=1/10
6/16= 3/8
2/18= 1/9
8/20=2/5
2/10= 1/5
Step-by-step explanation:
Triangle XYZ is rotated 90° counterclockwise using the origin as the center of rotation.
Which other rotation can be used to create triangle X’Y’Z’ from triangle XYZ?
90° clockwise
270° clockwise
270° counterclockwise
360° counterclockwise
Answers
The other rotation that can be used to achieve the transformation is; C: 270° counterclockwise
What is the rotation used?
From the coordinates of XYZ transformed to coordinates of triangle X'Y'Z', we can see that the transformation pattern is;
(x, y) -----> (-y, x)
Now, this pattern of transformation occurs when;
There is a 90° clockwise rotation. However, the other rotation that can be used to achieve this is a 270° counterclockwise rotation
Answer: Triangle XYZ can be rotated 90° counterclockwise using the origin as the center of rotation to create triangle X’Y’Z’. To obtain the original triangle XYZ, we need to rotate the triangle X'Y'Z' by 90° clockwise using the origin as the center of rotation. This means that rotating the triangle X'Y'Z' by 90° clockwise is the same as rotating triangle XYZ by 90° counterclockwise, so the answer is 90° clockwise.
Daniela scored
101
101101 points in
5
55 basketball games. Casey scored
154
154154 points in
8
88 games. Hope scored
132
132132 points in
7
77 games.
Casey tried to order the players by their points per game from least to greatest, but he made a mistake. Here's his work:
Answers
Hope, Casey, and Daniela are the players in order from lowest to highest points per game average.
To find the points per game for each player, we can divide their total points by the number of games they played:
Casey: 154 points ÷ 8 games = 19.25 points per game
Hope: 132 points ÷ 7 games = 18.86 points per game
Daniela: 101 points ÷ 5 games = 20.2 points per game
Casey mistakenly ordered the players as follows: Hope, Casey, and then Hope. This ordering is incorrect because Casey had a higher point-per-game average than Hope.
The correct ordering from least to greatest points per game average is: Hope, Casey, and then Daniela.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ1
Complete question:
Daniela scored
101 points in 5 basketball games. Casey scored 154 points in 8 games. Hope scored 132 points in 7 games. Casey tried to order the players by their points per game from least to greatest, but he made a mistake. Here's his work:
The absolute value of -1/4 is
Answers
Answer: 1/4
Explanation: Remember that the absolute value of a number is just the positive version of that number. So the absolute value of -1/4 is 1/4.