Find the missing information
Arc length = 13 m
Radius = ?
Central angle =45°
Would rlly appreciate it
Answers
\(\textit{arc's length}\\\\ s = \cfrac{\theta \pi r}{180} ~~ \begin{cases} r=radius\\ \theta =\stackrel{degrees}{angle}\\[-0.5em] \hrulefill\\ s=13\\ \theta =45 \end{cases}\implies 13=\cfrac{(45)\pi r}{180} \\\\\\ 13=\cfrac{\pi r}{4}\implies 52=\pi r\implies \cfrac{52}{\pi }=r\)
Related Questions
Salena has twice as many DVDs as Jolene,and Jolene has one third as many as Brodie.What fraction of the total DVDs has Salena?
Answers
Answer:
let jolene's dvd be x
2x+x+3x= total dvds = 6x
2x/6x=1/3
Salena has 1/3 of the total dvds
find the Total surface area of given figure)
nuem
1
20cm 24cm 14cm
Answers
Answer:
where is the figure? to calculate the surface area
please help me im doing pre alg and i cant figure out wether i shade up or to the side; graph x > 1
Answers
The representations of the inequality is an open circle is at 1 and a bold line starts at 1 and is pointing to the right.
How to graph an inequality?An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value e.g. 5 < 6, x ≥ 2, etc.
Since our answer is x > 1. An open circle will be at 1 and a bold line starts at 1 and is pointing to the right (>). Check the attached image.
Note: You only shade up if you have ≤ (less than or equal) or ≥ (greater than or equal).
Learn more about inequality on:
brainly.com/question/25275758
#SPJ1

If 6 pounds of apples cost $4.80 what is the cost per 9 pounds
Answers
Answer:
Cost of 1 pound apple:4.80/6=2.4
cost of 9 pounds apple:2.4 ×9=21.6
Please answer this correctly

Answers
Answer:
98.5
Step-by-step explanation:
64.4 x 2= 128.8
325.8-128.8=197.0
197 /2 = 98.5
brainliest plzz
Answer:
Hey mate,
here is your answer. Hope it helps you.
Step-by-step explanation:
x+x+64.4+64.4=325.8
2x+ 128.8 =325.8
2x = 325.8 - 128.8
2x = 197
x= 197/2
=98.5 inches
A table is made using the following two patterns.
Pattern x: Starting number: 1, Rule: add 1
Pattern y: Starting number: 5, Rule: add 5
Complete the table for the given patterns.
x y
1 5
Answers
Answer:
The required table will be
x y
1 5
2 10
3 15
4 20
5 25
Step-by-step explanation:
We are given 2 patterns
Pattern x: Starting number: 1, Rule: add 1
Pattern y: Starting number: 5, Rule: add 5
We need to complete the table for given patterns
x y
1 5
The second number for x according to pattern will be: we will add 1 to the previous number i.e 1+1 =2
The third number for x according to pattern will be: we will add 1 to the previous number i.e 2+1 =3
The second number for y according to pattern will be: we will add 5 to the previous number i.e 5+5 =10
The third number for y according to pattern will be: we will add 5 to the previous number i.e 10+5 =15
So, the required table will be
x y
1 5
2 10
3 15
4 20
5 25
As we are not given how much we need to fill table. I am adding 4 values for x and y.
please help me i really need help please i really need help please

Answers
Answer:
56.57 yards (rounded to the nearest hundredths)
Step-by-step explanation:
Well follow Pythagorean theorem
20^2+b^2=60^2
400+b^2=3600
B^2= 3200
√3200=56.57 (rounded)
(3n-9)+(1/5n+13)=(?+1/5n)+(-9+?)=?
Can u halp :C you need to simplify answer
Answers
Answer:
\(3\frac{1}{5}n\) + 4
Step-by-step explanation:
First Step: Write the equation
(3n - 9) + (\(\frac{1}{5}\)n + 13) =
Second Step: Combine like terms together
(3n + \(\frac{1}{5}\)n) + (-9 + 13)=
Third Step: Simplify
\(3\frac{1}{5}n\) + 4
Hope this helped! <3
No links help
Rectangle X is 5 cm long and 3 cm wide. Rectangle Y is similar to Rectangle X. What could be the dimensions of
Rectangle Y?
A)10 cm long and 8 cm wide
B)15 cm long and 9 cm wide
C) 15 cm long and 13 cm wide
D)10 cm long and 3 cm wide
Answers
Given
g
(
x
)
=
−
5
x
+
2
g(x)=−5x+2, find
g
(
4
)
g(4)
Answers
Answer:34
Step-by-step explanation:
A bag contains 6 blue chips, 3 red chips, 9 green chips, and 2 yellow chips. John pulls a chip out, records the colors, and returns the chip to the bag. He does this 200 times. How many times should John expect the color to be blue, red, or yellow?
Answers
Shape 1 and shape 2 are plotted on a coordinate plane. Which statement about the shapes is true?
A:
Shape 1 and shape 2 are not congruent.
B:
A translation will prove that shape 2 is congruent to shape 1.
C:
A rotation and a translation will prove that shape 2 is congruent to shape 1.
D:
A reflection, a rotation, and a translation will prove that shape 2 is congruent to shape 1

Answers
Answer:
A reflection, a rotation, and a translation will prove that shape 2 is congruent to shape 1.
Answer:
A reflection, a rotation, and a translation will prove that shape 2 is congruent to shape 1.
Step-by-step explanation:
Write an equation in slope intercept form to represent the values in the table.
x y
-2 -13
-1 -7
0 -1
1 5
2 11
answers y = 6x -1
y = -6x + 1
y = 6x +1
y = -6x -1
Answers
Answer:y=-6x-1
Step-by-step explanation:
Rafael and Roger played tennis against each other 30 times. Each of the times they played, either Rafael won or Roger won.
The ratio of the number of times Rafael won to the number of times Roger won is 7:3
(a) Work out the number of times Rafael won.
Answers
Answer:
Rafael won 21 times.
Step-by-step explanation:
Add 7 + 3 together = 10
30 divided by 10 = 3
3 x 7 = 21
Which of the following best describes the lines y-3x=4x and 6-2y=8x
○perpendicular
○parallel
○skew
○intersecting
Answers
Answer:
Intersecting (fourth answer choice)
Step-by-step explanation:
If the lines are perpendicular, parallel, or intersecting, they are not skew. Thus, we need to check if the lines can be classified as either perpendicular, parallel, or intersecting first. If the lines are classified as neither, then they are skew.First, let's convert both lines to slope-intercept form, whose general equation is y = mx + b, where
m is the slope,and b is the y-intercept.Converting y - 3x = 4x to slope-intercept form:
(y - 3x = 4x) + 3x
y = 7x
Thus, the slope of this line is 7 and the y-intercept is 0.
Converting 6 - 2y = 8x to slope-intercept form:
(6 - 2y = 8x) - 6
(-2y = 8x - 6) / -2
y = -4x + 3
Thus, the slope of this line is -4 and the y-intercept is 3.
Checking if y = 7x and y = -4x + 3 are perpendicular lines:
The slopes of perpendicular lines are negative reciprocals of each other.We can show this in the following formula:
m2 = -1 / m1, where
m1 is the slope of one line,and m2 is the slope of the other line.Thus, we only have to plug in one of the slopes for m1. Let's do -4.
m2 = -1 / -4
m2 = 1/4
Thus, the slopes 7 and -4 are not negative reciprocals of each other so the two lines are not perpendicular.
Checking if y = 7x and y = -4x + 3 are parallel lines:
The slopes of parallel lines are equal to each other.
Because 7 and -4 are not equal, the two lines are not parallel.
Checking if the lines intersect:
The intersection point of two lines have the same x and y coordinate. To determine if the two lines intersect, we treat them like a system of equations.Method to solve the system: Elimination:
We can multiply the first equation by -1 and keep the second equation the same, which will allow us to:
add the two equations, eliminate the ys, and solve for x:-1 (y = 7x)
-y = -7x
----------------------------------------------------------------------------------------------------------
-y = -7x
+
y = -4x + 3
----------------------------------------------------------------------------------------------------------
(0 = -11x + 3) - 3
(-3 = -11x) / 11
3/11 = x
Now we can plug in 3/11 for x in y = 7x to find y:
y = 7(3/11)
y = 21/11
Thus, x = 3/11 and y = 21/11
We can check our answers by plugging in 3/11 for x 21/11 for y in both y = 7x and y = -4x + 3. If we get the same answer on both sides of the equation for both equations, the lines intersect:
Checking solutions (x = 3/11 and y = 21/11) for y = 7x:
21/11 = 7(3/11)
21/11 = 21/11
Checking solutions (x = 3/11 and y = 21/11) for y = -4x + 3:
21/11 = -4(3/11) + 3
21/11 = -12/11 + (3 * 11/11)
21/11 = -12/11 + 33/11
21/11 = 21/11
Thus, the lines y = 3x = 4x and 6 - 2y = 8x are intersecting lines (the first answer choice).
This also means that lines are not skew since lines had to be neither perpendicular nor parallel nor intersecting to be skew.
distribute than combine like terms
8(3x+2y-7)+5(4x+8y-2)
THANK YOU
Answers
Then
44x+56y-56-10
Then
44x+56y-66
p(5)=
p(1 or 2)=
p(odd number)=
p(not 6)=
p(even number)=
p(1,2,3,or 4)=
Answers
The probabilities, we need to understand the context. Assuming we are working with a fair six-sided die, where each face has an equal chance of landing, here are the probabilities:
P(5): Since there is only one face with a value of 5 on the die, the probability of rolling a 5 is 1/6.P(1 or 2): There are two faces with the values 1 and 2 respectively. Since these are mutually exclusive events (you can only roll one of them at a time), the probability of rolling a 1 or a 2 is 2/6, which simplifies to 1/3.P(odd number): Out of the six faces, three are odd numbers (1, 3, and 5). So, the probability of rolling an odd number is 3/6, which simplifies to 1/2.P(not 6): Since there is only one face with a value of 6, the probability of not rolling a 6 is 5/6.P(even number): Out of the six faces, three are even numbers (2, 4, and 6). So, the probability of rolling an even number is 3/6, which simplifies to 1/2.P(1, 2, 3, or 4): There are four faces with the values 1, 2, 3, and 4. Therefore, the probability of rolling any of these numbers is 4/6, which simplifies to 2/3.For such more questions on probability
https://brainly.com/question/30390037
#SPJ8
Determine whether the given function is a solution to the given differential equation.
x =2cost - 3sint, x'' +x =0
Answers
Given :
A function , x = 2cos t -3sin t .....equation 1.
A differential equation , x'' + x = 0 .....equation 2.
To Find :
Whether the given function is a solution to the given differential equation.
Solution :
First derivative of x :
\(x'=\dfrac{d(2cos t - 3sin t)}{dt}\\\\x'=\dfrac{d(2cost)}{dt}-\dfrac{(3sint)}{dt}\\\\x'=-2sint-3cost\)
Now , second derivative :
\(x''=\dfrac{d(-2sint-3cost)}{dt}\\\\x''=-\dfrac{d(2sint)}{dt}-\dfrac{d(3cost)}{dt}\\\\x''=-2cost+3sint\)
( Note : derivative of sin t is cos t and cos t is -sin t )
Putting value of x'' and x in equation 2 , we get :
=(-2cos t + 3sin t ) + ( 2cos t -3sin t )
= 0
So , x'' and x satisfy equation 2.
Therefore , x function is a solution of given differential equation .
Hence , this is the required solution .
What is the slope and y-intercept of y = 4x
Answers
Answer: Slope: 4 Y-intercept: 0
Step-by-step explanation:
In a comparison of the body fat percentage of four different ethnic groups, the body fat percentage was measured for 200 African-Americans, 160 Whites, 220 Hispanics, and 310 Others. Because a comparison of average body fat percentage between these groups is desired, an ANOVA test was conducted, which resulted in p-value of 0.11. What conclusion can you make if level of significance is 0.05?
Answers
Answer:
There is not enough evidence to support the claim that the fat percentage of at least one of the four ethnic groups is different.
Step-by-step explanation:
The Analysis of Variance (ANOVA) test is used to determine whether there is any significant difference between the mean of various independent groups.
In this case an ANOVA test is being performed to determine whether the fat percentage of four different ethnic groups are different or not.
The hypothesis can be defined as:
H₀: The fat percentage of four different ethnic groups are same, i.e. μ₁ = μ₂ = μ₃ = μ₄.
Hₐ: The fat percentage of at least one of the four ethnic groups is different, i.e. at least one μ\(_{i}\) is different.
The significance level of the test is, α = 0.05.
The decision rule is:
If the p-value of the test is less than the significance level, then the null hypothesis will be rejected.And if the p-value of the test is not less than the significance level, then the null hypothesis will not be rejected.The p-value of the ANOVA test is computed as, p-value = 0.11.
p-value = 0.11 > α = 0.05.
The null hypothesis was failed to be rejected.
Hence, it can be concluded that there is not enough evidence to support the claim that the fat percentage of at least one of the four ethnic groups is different.
Astronomers measure large distances in light-years. One light-year is the distance that light can travel in one year, or approximately 5,880,000,000,000 miles. Suppose a star is 13.6 light-years from Earth. In scientific notation, how many miles away is it?
a)5.88 × 1012 miles
b)7.9968 × 1013 miles
c)5.88 × 1013 miles
d)1.36 × 1012 miles
Answers
Answer:
b) 7.9968 × 1013 miles
Step-by-step explanation:
So one light-year equals 588 × 10^10
13.6 light-years equals 13.6 × 588 × 10^10 = 79968 × 10^9 = 7.9968 × 1013 miles
Inequalities - Introduction
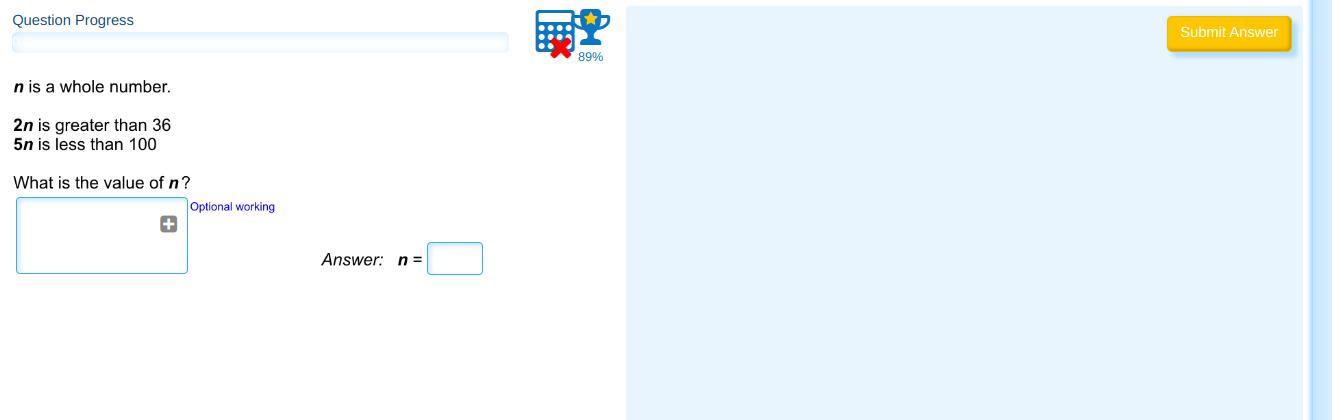
Answers
Answer:
n = 19
Step-by-step explanation:
2n > 36 ( divide both sides by 2 )
n > 18
and
5n < 100 ( divide both sides by 5 )
n < 20
so n > 18 and n < 20
thus n = 19
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1

Question
A card is drawn from a standard deck of 52 cards and then placed back into the deck. Find the probability that a red card is
drawn at least once by the third draw. Round your answer to two decimal places.
Provide your answer below:
Answers
The probability that a red card is drawn at least once by the third draw is 0.88.
What is probability?
The area of mathematics known as probability deals with numerical descriptions of how likely it is for an event to happen or for a claim to be true. A number between 0 and 1 is the probability of an event, where, broadly speaking, 0 denotes the event's impossibility and 1 denotes its certainty.
Let, a card is drawn from a standard deck of 52 cards and then placed back into the deck.
In a standard 52 card deck the red cards are 26.
So,
P(red) = n(red cards) / n(total cards)
= 26 / 52
P(red) = 0.50
Now, X ≈ Bin (n = 3, P = 0.50)
P(X = x) = (n x) p^x (1 - p)^n-x
(n x) = \(\frac{n!}{x!(n-x)!}\)
P(X ≥ 1) = 1 - P(X < 1)
= 1 - P(X = 0)
= 1- (3 0)(0.5)^0(0.5)^3
= 1 - 0.125
= 0.875
P(X ≥ 1) = 0.88
Hence, the probability that a red card is drawn at least once by the third draw is 0.88.
To know more about the probability, click on the link
https://brainly.com/question/24756209
#SPJ1
6x8 = nx 16
What is the value of the unknown number?
Answers
A box contains 2 red marbles, 5 green marbles and 8 blue marbles. Find the probability of the different events.
P ( 3 blue ) =
P (blue & green)
Answers
The value of the probability of the different events are,
The value of the probability P (3) is,
⇒ 1 / 5
And, The value of the probability P (blue & green) is,
⇒ 8/45
We have to given that;
A box contains 2 red marbles, 5 green marbles and 8 blue marbles.
Hence, Total marbles = 2 + 5 + 8 = 15
So, The value of the probability P (3) is,
⇒ 3 / 15
⇒ 1 / 5
And, The value of the probability P (blue & green) is,
⇒ 8/15 x 5/15
⇒ 8/15 x 1/3
⇒ 8 / 45
Thus, The value of the probability P (3) is,
⇒ 1 / 5
And, The value of the probability P (blue & green) is,
⇒ 8/45
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
Which relation is a function?

Answers
The only graph that represents a function is: Graph D
How to identify a function?A function is defined as a relationship or expression that involves one or more variables. It typically has a set of input and outputs. Each input has only one output. The function is the description of how the inputs relate to the output.
A function is a relation which describes that there should be only one output for each input (or) we can say that a special kind of relation (a set of ordered pairs), which follows a rule i.e., every X-value should be associated with only one y-value is called a function.
From the graphs, we can see that:
Graph A has 2 outputs at x = -2
Graph B has 2 outputs at x = 0
Graph C has two outputs at x = -1
Graph D has a unique output for every input and as such it is a function
Read more about function description at: https://brainly.com/question/24057830
#SPJ1
Find the average rate of change where x=3 and x=5
Answers
Let's assume we have a function f(x) and we want to find the average rate of change between x=3 and x=5. We can use the following formula to calculate the average rate of change:
Average rate of change = (f(5) - f(3)) / (5 - 3)
This formula gives us the slope of the line connecting the two points. We can then interpret this slope as the average rate of change between the two points.
For example, if f(x) = 2x + 1, then:
f(3) = 2(3) + 1 = 7
f(5) = 2(5) + 1 = 11
So, the average rate of change between x=3 and x=5 is:
Average rate of change = (11 - 7) / (5 - 3) = 2
Therefore, the average rate of change between x=3 and x=5 is 2.
A tank contains 5,000 L of brine with 13 kg of dissolved salt. Pure water enters the tank at a rate of 50 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate.
Required:
a. How much salt is in the tank after t minutes?
b. How much salt is in the tank after 20 minutes?
Answers
Answer:
a) \(x(t) = 13*e^(^-^\frac{t}{100}^)\)
b) 10.643 kg
Step-by-step explanation:
Solution:-
- We will first denote the amount of salt in the solution as x ( t ) at any time t.
- We are given that the Pure water enters the tank ( contains zero salt ).
- The volumetric rate of flow in and out of tank is V(flow) = 50 L / min
- The rate of change of salt in the tank at time ( t ) can be expressed as a ODE considering the ( inflow ) and ( outflow ) of salt from the tank.
- The ODE is mathematically expressed as:
\(\frac{dx}{dt} =\) ( salt flow in ) - ( salt flow out )
- Since the fresh water ( with zero salt ) flows in then ( salt flow in ) = 0
- The concentration of salt within the tank changes with time ( t ). The amount of salt in the tank at time ( t ) is denoted by x ( t ).
- The volume of water in the tank remains constant ( steady state conditions ). I.e 10 L volume leaves and 10 L is added at every second; hence, the total volume of solution in tank remains 5,000 L.
- So any time ( t ) the concentration of salt in the 5,000 L is:
\(conc = \frac{x(t)}{1000}\frac{kg}{L}\)
- The amount of salt leaving the tank per unit time can be determined from:
salt flow-out = conc * V( flow-out )
salt flow-out = \(\frac{x(t)}{5000}\frac{kg}{L}*\frac{50 L}{min}\\\)
salt flow-out = \(\frac{x(t)}{100}\frac{kg}{min}\)
- The ODE becomes:
\(\frac{dx}{dt} = 0 - \frac{x}{100}\)
- Separate the variables and integrate both sides:
\(\int {\frac{1}{x} } \, dx = -\int\limits^t_0 {\frac{1}{100} } \, dt + c\\\\Ln( x ) = -\frac{t}{100} + c\\\\x = C*e^(^-^\frac{t}{100}^)\)
- We were given the initial conditions for the amount of salt in tank at time t = 0 as x ( 0 ) = 13 kg. Use the initial conditions to evaluate the constant of integration:
\(13 = C*e^0 = C\)
- The solution to the ODE becomes:
\(x(t) = 13*e^(^-^\frac{t}{100}^)\)
- We will use the derived solution of the ODE to determine the amount amount of salt in the tank after t = 20 mins:
\(x(20) = 13*e^(^-^\frac{20}{100}^)\\\\x(20) = 13*e^(^-^\frac{1}{5}^)\\\\x(20) = 10.643 kg\)
- The amount of salt left in the tank after t = 20 mins is x = 10.643 kg
Over a period of one year, a retailer sells widgets at 11
different prices. He Calculates the average number of oiunds sold per day at each different price. From theese data, the following are calculated.
Answers
The regression equation is: y = -0.0068824x + 36.8881
So, the correct option is:
D) None of these.
To compute the regression equation based on the given data, we can use the formulas for slope (b1) and y-intercept (bo):
b1 = (NΣXY - ΣXΣY) / \((N\sum X^2 - (\sum X)^2)\)
bo = (ΣY - b1ΣX) / N
Where:
N = Number of data points (in this case, 11)
ΣX = Sum of all X values (prices)
ΣY = Sum of all Y values (average number of pounds sold per day)
ΣXY = Sum of the product of X and Y values
\(\sum X^2\) = Sum of the squares of X values
Using the provided data:
Ex = 210
Xy = 450
Zcy = 10387
Zz = 7275
Xy = 42471
Let's calculate the required values:
N = 11
ΣX = Ex + Zcy + Zz = 210 + 10387 + 7275 = 17872
ΣY = Xy = 450
ΣXY = Xy = 450
\(\sum X^2 = (Ex)^2 + (Zcy)^2 + (Zz)^2 = (210)^2 + (10387)^2 + (7275)^2 = 239208144\)
Now, substitute these values into the formulas to find b1 and bo:
\(b1 = (11 \times450 - 17872 \times 450) / (11 \times239208144 - (17872)^2)\)
= -14112250 / 2050445128
≈ -0.0068824
bo = (450 - (-0.0068824 \(\times\) 17872)) / 11
= (450 + 122.7790368) / 11
≈ 36.8881
Therefore, the regression equation is:
y = -0.0068824x + 36.8881
So, the correct option is:
D) None of these.
For similar question on regression equation.
https://brainly.com/question/25987747
#SPJ8
The complete question may be like:
Over a period of one year, retailer sells widgets at 11 different prices. He Calculates the average number of oiunds sold per day at each different price. From theese data, the following are calculated. Ex = 210, Xy = 450, Zcy = 10387, Zz? 7275 Xy? 42471 Compute the regression equation , SELEC A) y 0.20261x + 0.549951 B) y = 0.549951x + 30.410021 C) y = 0.20261. + 30.410021 D) none of these =b1x + bo.