Answers
Answer:
19.2
Step-by-step explanation:
It's right on Acellus.
The required value of x nearest to tenth is 19.17
What is hypotenuse?The longest side of the right angled triangle is called hypotenuse
By the Pythagoras theorem in the right angled triangle
h^2 = b^2 + p^2
where h = hypotenuse, b = base, p = perpendicular
How to calculate hypotenuse?Here we have given perpendicular p = 9
and an angle = 28°
Using sin for the given angle we have
sin 28° = \(\frac{perpendicular}{hypotenuse}\)
0.46947 = \(\frac{9}{x}\)
x = \(\frac{9}{0.46947}\)
x = 19.17
Hence the required length of the side hypotenuse = x = 19.17
This is the conclusion to the answer.
Learn more about hypotenuse here-
https://brainly.com/question/2217700
#SPJ2
Related Questions
Someone please help answer !
Choose the number that is closest to the mean of the distribution

Answers
The mean of the distribution is 3
What is arithmetic mean?Arithmetic mean is defined as the ratio of the sum of observations to the total number of observations. It can be referred to as the average of a specific set of data or the arithmetic mean. One of the basic methods used to acquire a result, the term "Mean" is commonly used in the field of statistics.
The formula for the mean of a given set of data is as follows:
Mean = Sum of Observations/Total number of observations
According to the first graph,
Given the bar of observations as :
0, 5, 6, 3, 1, 1, 3, 6, 4, 1
Here the Sum of Observations = 30
And the total number of observations = 10
The mean of the distribution = 30/10
The mean of the distribution = 3
According to the second graph,
Given the bar of observations as :
0, 1, 3, 3, 9, 0, 9, 4, 4, 1
Here the Sum of Observations = 34
And the total number of observations = 10
The mean of the distribution = 34/10
The mean of the distribution = 3.4
The mean of the distribution = 4 (closest)
Learn more about Arithmetic means here:
brainly.com/question/13000783
#SPJ1
ASAP please A hotel reservation code consists of 4 single-digit numbers followed by 3 letters.
How many different reservation codes are possible?
Answers
Answer:
175760000 possible reservation codes
Step-by-step explanation:
Repetition of numerals or letters is permitted in the context of the question.
There are ten options for each digit (even a leading zero is considered a reservation number), and 26 options for each letter (normally upper and lower cases are considered identical). So,
Possible reservations = 10*10*10*10*26*26*26
=10^4*26^3
=175760000
The number of different reservation codes possible are 175760000.
Given that, a hotel reservation code consists of 4 single-digit numbers followed by 3 letters.
What is the Permutations?Permutations are different ways of arranging objects in a definite order. It can also be expressed as the rearrangement of items in a linear order of an already ordered set. The symbol nPr is used to denote the number of permutations of n distinct objects, taken r at a time.
From the context of the question, repetition of digits or letters are allowed.
For each digit, there are 10 possible choices (even a leading zero is considered a reservation number), and for each letter, there are 26 letters (normally upper and lower cases are considered identical).
So, number of ways =10×10×10×10×26×26×26
=10000×17576
=175760000
Hence, the number of different reservation codes possible are 175760000.
To learn more about the permutation visit:
https://brainly.com/question/3867157.
#SPJ2
I need help asap please!!!

Answers
The values of the angles given are: 0,90,180,240,270,360,420,480,540,600,630,660,720 and
What is sine of angles?he sine of an angle is the trigonometric ratio of the opposite side to the hypotenuse of a right triangle containing that angle. It is defined as the length of the opposite side divided by the length of the hypotenuse
The given angles are: 0,30,45,90,120,135,180,210,225,240,270,300,315,330,360
2∅ 2*∅ = 0, 90,180,240,270,360,420,480,540,600,630,660,720
sin 2∅ = sin0 = 0; Sin90=1; sin180=0; sin240= -0.8660; sin270 = -1;
Each angle is multiplied by sine sine360 =1; sin420 = 0.8660; sin480= 0.9848; sin540=1; sin600=-0.8660; sin630=-1; sin660=0.8660; sin720= 0.9397
Learn more about sine of angles on https://brainly.com/question/22649800
#SPJ1
The values in the table represent a function.
A 2-column table with 5 rows. The first column is labeled x with entries negative 6, 7, 4, 3, negative 5. The second column is labeled f of x with entries 8, 3, negative 5, negative 2, 12.
Use the drop-down menus to complete the statements.
The ordered pair given in the first row of the table can be written using function notation as
.
f(3) is
.
f(x) = –5 when x is
.
Answers
The correct answers are:
f(-6) = 8f(3) = -2f(x) = -5 when x is 4What is the function?Functions are expressions separated by an equal sign. They have both dependent and independent variables.
How to solve* Lets explain how to solve the problem
- The table of the function has two column
# First column labeled x with entries:
-6 , 7 , 4 , 3 , -5
# Second column labeled f(x) with entries:
8 , 3 , -5 , -2 , 12
∴ The ordered pairs of the function f(x) are:
(-6 , 8) , (7 , 3) , (4 , -5) , (3 , -2) , (-5 , 12)
* Lets complete the missing
∵ The value of x in the first row is -6
∵ The value of f(x) in the first row is 8
∴ The function notation in the 1st row is f(-6) = 8
- The ordered pair given in the first row of the table can be
written using function notation as f(-6) = 8
∵ The ordered pair whose x = 3 is (3 , -2)
∴ The value of f(x) when x = 3 is -2
∴ f(3) = -2
∵ The ordered pair whose f(x) = -5 is (4 , -5)
∴ The value of x when f(x) = -5 is 4
∴ f(x) = -5 when x is 4
To learn more about the function visit, https://brainly.com/question/28278690
How many roots do the functions have in common f(x)=x^2+x-6
Answers
To find the common roots between two functions, we need to find the roots (or solutions) of each function individually and then identify the shared solutions.
For the function f(x) = x^2 + x - 6, we can find the roots by setting the function equal to zero and solving for x:
x^2 + x - 6 = 0
To factorize this quadratic equation, we need to find two numbers that multiply to -6 and add up to 1 (the coefficient of x). The numbers that satisfy these conditions are 3 and -2:
(x + 3)(x - 2) = 0
Setting each factor equal to zero:
x + 3 = 0 or x - 2 = 0
Solving for x in each equation:
x = -3 or x = 2
Therefore, the function f(x) = x^2 + x - 6 has two roots: x = -3 and x = 2.
To find the common roots between this function and another function, we would need to know the second function. If you provide the second function, I can help determine if there are any shared roots.
Darrius scored 63 points in 4 games. What was his rate of points per game?
Answers
= 63 / 4
= 15.75 points per game.
Answer:
15.75
Step-by-step explanation:
63÷4=15.75
hope you understand
8.2: Word Problems - UNDERLINE key words, set up your division sentence, then solve!
Ms. K's cooking club needs 2 1/4 cups of flour to make enough crepes for everyone in the class. The
club split into 6 smaller groups, each making their own batch. How much flour does each group
need?
Answers
Answer:
3/8
Step-by-step explanation:
hope it helps :)
what fraction is the same as 42%
Answers
hmu for extra math help
a student spends 18 out of 35 of his pocket money on transport and fruit what is the fraction left?
Answers
To find the fraction of pocket money left after spending on transport and fruit, we need to subtract the amount spent from the total pocket money and express it as a fraction.
The student spends 18 out of 35 of his pocket money, which means he has (35 - 18) = 17 units of his pocket money left.
Therefore, the fraction of pocket money left can be written as 17/35.
PLS HELP! The picture is down below

Answers
Please mark brainliest when you can
A box is a cuboid with dimensions 26cm by 15cm by 20 cm all measured to the nearest centimetre. Disc cases are cuboids which measure 1.6cm by 14.2cm by 19.3cm all measured to the nearest millimetre. If the disc cases are stacked as shown, show that it may not be possible for 16 cases to fit in the box
Answers
Answer: length of box , l =26 cm , breadth , b =15 cm , height = 20 cm
So,the volume of the box = l × b × h
= 26 × 15 ×20 cm3
= 7800 cm3
Now length of a disc case, l= 1.6 cm
breadth ,b =14.2 cm
height, h =19.3 cm
So the volume of a disc case = 1.6×14.2×19.3 cm3
= 438.496 cm3
No of disc cases can be stacked inside the box
= 7800 ÷ 438.496
=7800000÷438.496
= 17.8
Hence 17 disc cases can be fitted into the box.
Step-by-step explanation:
A woman bought some large frames for $10 each and some small frames for $4 each at a closeout sale. If she bought 22 frames for $106, find how many of each type she bought.
Answers
Answer:
19 small frames and 3 large frames
Step-by-step explanation:
follows the steps in the attached

A bottle contains 3.6 liters of water, water drips out of the bottom of the bottle at a rate of 20 millilitres per minute, work out how long it takes for the bottle to empty, give your answer in hours.
Answers
Answer: 3 hours
Step-by-step explanation:
Bottle = 3.6 liters / 3600 milliliters
Rate = 20 ml a minute
3600 / 20 = 180 minutes
60 minutes = 1 hour
180 / 60 = 3 hours
A quadratic function has its vertex at the point
(
2
,
−
10
)
(
2
,
-
10
)
. The function passes through the point
(
−
6
,
−
5
)
(
-
6
,
-
5
)
. Find the quadratic and linear coefficients and the constant term of the function.
Answers
the standard form equation is y=ax²+bx+c where a is the quadratic coefficient, b is the linear coefficient, and c is the constant coefficient.
therefore, for y = 5/16x² - 5x/4 -35/4
Quadratic coefficient = 5/16, linear coefficient = 5/4, constant term = -35/4
What are zeros ?
zeros denotes the factors of the given equation in other words the zeros of the function are the values that make the factors zero. The factors need to multiply out to give the original standard-form equation.
Polynomial roots are the same as polynomial zeros, so they can be found by factoring the quadratic equation into two linear factors, after which they can be equating to zero.
Its easiest to first start out with a vertex form equation because it can then be converted to a standard quadratic equation.
given a vertex at (2,-10) , and point of intersection at (6,-5), the equation can be set up like this in the form of :
y = a(x-h)²+ k
y = a(x-2)^2-10, as we know h and k from the vertex.
We also know y and x from the given point of intersection so a can be solved by substituting the values of x and y to get value of a.
y = a(x-2)²-10
-5 = a(6-2)² - 10
16a = 10-5
a = 5/16
a = 5/16 which is also known as the quadratic coefficient because it is part of a second degree quantity and a Trinomial as a whole(quadratic).
since all the variables are known, you can expand the equation and set it to standard form :
y = 5/16(x-2)²-10
y = 5/16(x-2)² - 10
y = 5/16(x²+4-4x) -10
y = 5/16x² + 5/4 - 5x/4 - 10
y = 5/16x² - 5x/4 -35/4
For reference, the standard form equation is y=ax²+bx+c where a is the quadratic coefficient, b is the linear coefficient, and c is the constant coefficient.
In this instance, 5/16x² - 5x/4 -35/4 = ax²+bx+c
Learn more on quadratic function here:
https://brainly.com/question/21442266
#SPJ1
Triangles ABC and YZX are similar. Use the measurements given in the image below to find the side length of ZX. In your answer, give the side length of ZX and explain how you calculated it. X А 25 Y 40 50 20 Z UD 60 C (100 points if it's correct)

Answers
Answer:
ZX = 30 unitsStep-by-step explanation:
Since the triangles are similar, the ratio of corresponding sides are same.
ZX is the largest side and corresponding side is BC = 60, the shortest sides are BC = 40 and YZ = 20:
ZX / 60 = 20/40ZX / 60 = 1/2ZX = 60/2ZX = 30Need helpppppppppppppppp

Answers
Answer:
\(46\%\)
Step-by-step explanation:
let the percentage be x
\( 37 \times x\% = 17\\ 37 \times \frac{x}{100} = 17 \\ \frac{37x}{100} = 17 \\ x = \frac{17 \times 100}{37} \\ x = 45.94\%\)
At a factory that produces pistons for cars, Machine 1 produced 174 satisfactory pistons and 116 unsatisfactory pistons today. Machine 2 produced 180 satisfactory pistons and 20 unsatisfactory pistons today. Suppose that one piston from Machine 1 and one piston from Machine 2 are chosen at random from today's batch. What is the probability that the piston chosen from Machine 1 is satisfactory and the piston chosen from Machine 2 is unsatisfactory
Answers
Answer:
\(0.7\) is the probability that the piston chosen from Machine 1 is satisfactory and the piston chosen from Machine 2 is unsatisfactory
Step-by-step explanation:
The two events are independent of each other.
Hence the probability of choosing satisfactory piston from Machine 1 and unsatisfactory piston from Machine 2 is equal probability of choosing satisfactory piston from Machine 1 + probability of choosing unsatisfactory piston from Machine 2
Substituting the given values we get
Probability of choosing satisfactory piston from Machine 1 and unsatisfactory piston from Machine 2 =\(\frac{174}{174 +116} + \frac{20}{180 +20}\)
=\(\frac{174}{174 +116} + \frac{20}{180 +20}\)
=\(= \frac{174}{290} + \frac{20}{200}\\= 0.6 + 0.1\\= 0.7\)
You measure 48 backpacks' weights, and find they have a mean weight of 70 ounces. Assume the population standard deviation is 6.4 ounces. Based on this, construct a 99% confidence interval for the true population mean backpack weight.
Give your answers as decimals, to two places
Answers
The 99% confidence interval for the true population mean backpack weight is approximately (68.15, 71.85) ounces, rounded to two decimal places.
To construct a 99% confidence interval for the true population mean backpack weight, we can use the formula:Confidence Interval = Sample Mean ± (Critical Value * Standard Deviation / √Sample Size).
Since the population standard deviation is known, we can use the z-distribution and find the critical value corresponding to a 99% confidence level. The critical value for a 99% confidence level is approximately 2.576.
Given that the sample mean weight is 70 ounces, the population standard deviation is 6.4 ounces, and the sample size is 48, we can calculate the confidence interval:
Confidence Interval = 70 ± (2.576 * 6.4 / √48).
Simplifying the expression, we get:
Confidence Interval ≈ 70 ± 1.855.
For more such questions on weight
https://brainly.com/question/2335828
#SPJ8
14. Simon earned 400sh as a for goods sold what Commission 15,000 worth so, 600 could be his varnings for a total sale of 7,000
Answers
His total earnings for a total sale of 7,000 could be 1450sh
How to determine his earnings for a total sale of 7,000.From the question, we have the following parameters that can be used in our computation:
Salary = 400
Commission = 15%
using the above as a guide, we have the following:
Total earnings = 400 + 15% * Total sales
So, we have
Total earnings = 400 + 15% * 7000
Evaluate
Total earnings = 1450
Hence, the total earnings is 1450
Read more about commission at
https://brainly.com/question/26283663
#SPJ1
Question
Simon earned 400sh weekly for goods sold and a commission of 15%
What could be his earnings for a total sale of 7,000.
A piece of lumber 2.8 meters long weighs 24.5 kilograms. A piece 0.8 meter long is cut from
the 2.8-meter length. Determine the weight of the 0.8-meter piece.
Answers
The weight of the 0.8-meter piece is 19.6 kilograms.
We can use the ratio of length to weight to determine the weight of the 0.8-meter piece.
Let's call the weight of the 2.8-meter piece "W₁" and the weight of the 0.8-meter piece "W₂". Then we have:
W₁/2.8m = 24.5kg/1m
Solving for W₁, we get:
W₁ = (24.5kg/1m) x 2.8m = 68.6kg
Now we can use the same ratio to find W₂:
W₂/0.8m = 24.5kg/1m
Solving for W₂, we get:
W₂ = (24.5kg/1m) x 0.8m = 19.6kg
Therefore, the weight of the 0.8-meter piece is 19.6 kilograms.
To learn more on Ratios click:
https://brainly.com/question/1504221
#SPJ1
If (x -1) is a factor of the polynomial f(x) = 4x²- 4x² - x - K, where K is a Constant.
1. What is the Value of K?
2. What are the roots of the equation
Answers
Answer:
If (x-1) is a factor of the polynomial f(x) = 4x² - 4x² - x - K, then we know that (x-1) divides evenly into the polynomial, which means that the polynomial can be written as:
f(x) = (x-1)(ax + b)
where a and b are constants that we need to determine. We can use the distributive property to expand this expression and equate it with the original polynomial:
f(x) = (x-1)(ax + b) = 4x² - 4x - K
Expanding the left side of the equation, we get:
ax² + bx - ax - b = ax² - (a-b)x - b = 4x² - 4x - K
Now we can equate the coefficients of the like terms on both sides of the equation.
The coefficient of x^2 on the left side is a, and on the right side it is 4. Therefore, we have:
a = 4
The coefficient of x on the left side is b - a, and on the right side it is -4. Therefore, we have:
b - a = -4
Substituting a=4, we get:
b - 4 = -4
Solving for b, we get:
b = 0
So the polynomial can be written as:
f(x) = (x-1)(4x + 0) = 4x² - 4x
Therefore, K = 0.
To find the roots of the equation, we need to set f(x) = 0 and solve for x:
4x² - 4x = 0
Factor out 4x:
4x(x - 1) = 0
So the roots of the equation are x = 0 and x = 1.
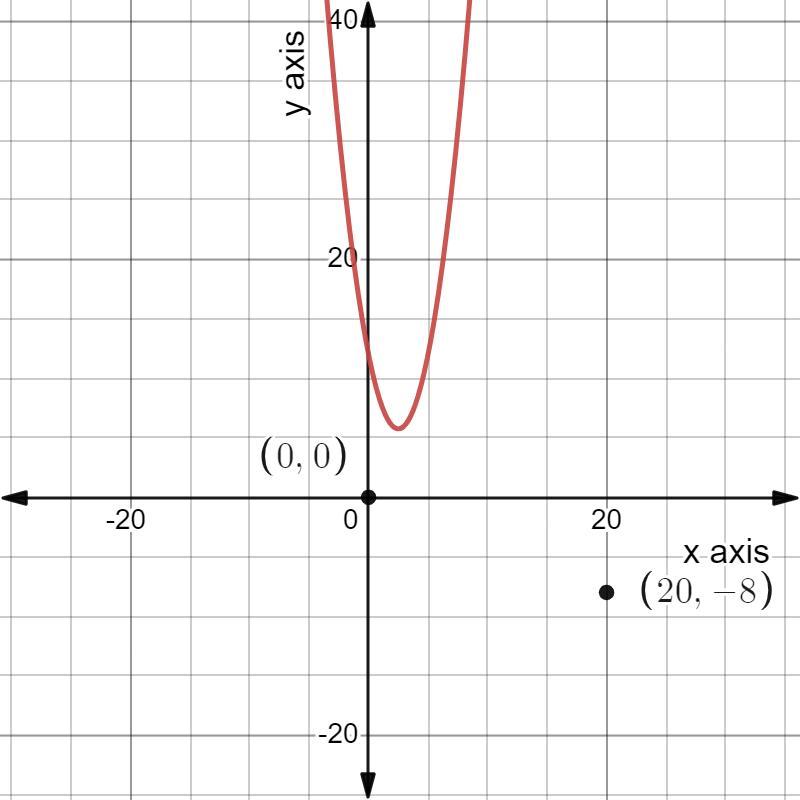
Consider the quadratic function f(x) = x2 – 5x + 12. Which statements are true about the function and its graph? Select three options. The value of f(–10) = 82 The graph of the function is a parabola. The graph of the function opens down. The graph contains the point (20, –8). The graph contains the point (0, 0).
Answers
The statement that are true about the function and its graph is "The graph of the function is a parabola " , the correct option is (b) .
In the question ,
it is given that ,
the quadratic function is f(x) = x² – 5x + 12 .
for x = -10 ,
f(-10) = (-10)² – 5(-10) + 12
= 100 + 50 + 12
= 162
option(a) is false .
the graph of the quadratic function is shown below .
form the graph we can see that the graph is a parabola ,
and the function opens upwards ,
the graph does not contain the points (20,-8) and (0,0)
Therefore , The statement that are true about the function and its graph is "The graph of the function is a parabola " , the correct option is (b) .
The given question is incomplete , the complete question is
Consider the quadratic function f(x) = x² – 5x + 12. Which statement is true about the function and its graph?
(a) The value of f(–10) = 82
(b) The graph of the function is a parabola.
(c) The graph of the function opens down.
(d) The graph contains the point (20, –8).
(e) The graph contains the point (0, 0).
Learn more about Functions here
https://brainly.com/question/13159926
#SPJ1
5x = -4y + 4 please help me
Answers
I THINK X IS 5/4 ANY ANSWER CHOISES ??
What value of x makes the equation 3(x−6)−8x=−2+5(2x+1) true?
Answers
Answer:
\(3(x - 6) - 8x = - 2 + 5(2x + 1) \\ 3x - 18 - 8x + 2 - 10x - 5 = 0 \\ = > - 15x - 21 = 0 = > - 15x = 21 = > x = - \frac{7}{5} \)
One year, the closest the moon got to Earth was 372,835 kilometers.
The farthest distance from the moon to Earth was 401,830 kilometers.
What is the difference between the two distances?
ANSWERS CHOICES-
31,005 kilometers
30,995 kilometers
28,995 kilometers
29,995 kilometers
97 POINTS!
Answers
Answer:
28,995 kilometers
Step-by-step explanation:
401,830-372,835= 28995
Answer:
28,995
Step-by-step explanation:
401,830
-372,835
28,995
Match each expression with A, B, C or D.
A=a^3
B=6a
C=12a
D=3a^2
i)3a x 4
ii)a^2xa
iii) 6 1/2 a^2

Answers
The matching expressions are:
\(i) 3a x 4 = C (12a)\\ii) a^2 x a = A (a^3)\\iii) 6 × 1/2 a^2 = D (3a^2)\)
i) 3a x 4 can be represented as C (12a) since multiplying 3a by 4 gives 12a.
ii) a^2 x a can be represented as A (a^3) since multiplying a^2 by a gives a^3.
iii) \(6 \times 1/2 a^2\) can be represented as D (3a^2) since multiplying 6 by 1/2 and then by a^2 gives 3a^2.
To understand the matching expressions, let's break down each one:
i) 3a x 4:
This expression represents multiplying a variable, 'a', by a constant, 4. The result is 12a, which matches with C (12a).
ii) a^2 x a:
This expression represents multiplying the square of a variable, 'a', by 'a' itself. This results in a^3, which matches with A (a^3).
iii) 6 × 1/2 a^2:
This expression involves multiplying a constant, 6, by a fraction, 1/2, and then multiplying it by the square of 'a', a^2. The final result is 3a^2, which matches with D (3a^2).
Therefore, the matching expressions are:
i) 3a x 4 = C (12a)
ii) a^2 x a = A (a^3)
iii) 6 × 1/2 a^2 = D (3a^2)
for such more question on matching expressions
https://brainly.com/question/12270624
#SPJ8
Evaluate if f(x)=x+8+15,g(x)4x-2andh(x)=x-5x-14

Answers
Find the diagonal of a square whose sides measure 3x square root of 2
Answers
Answer:
that means each side equals 8
Step-by-step explanation:
The cost of dress in a shop is 320.00 for more than more than the cast: If a customer of a pair of pays 305.00 for the turo items. How much does each cost.
Answers
The price of each of these be
A dress market at Rs.120 is 96A pair of shoes market at Rs.750 is 600A bag market at Rs.250 is 200.What is discount?The discount is determined by dividing the purchase price by the item's par value. Discount is a type of cost price reduction or deduction for a product. It is primarily employed in consumer interactions when discounts on various goods are offered to customers. A percentage represents the discount rate. (Discount List Price) 100 is the formula used to determine the rate of discount. The discount is the amount that is subtracted from the selling price in the formula. [(List price - Selling price)/List price] 100 is an additional formula for computing discount percentages.The simplest definition of a price is the sum of money exchanged by a buyer and seller for a good or service.A. Price \(}=\left(\frac{100 \%-20 \%}{100 \%}\right) * 120=\frac{80}{100} * 120=96 \\\)
B. Price =\(\left(\frac{100 \%-20 \%}{100 \%}\right) * 750=\frac{80}{100} * 750=600 \\\)
C. Price \(=\left(\frac{100 \%-20 \%}{100 \%}\right) * 250=\frac{80}{100} * 250=200\)
The complete question is.
A shop gives 20% discount. What would the price of each of these be?
A dress market at Rs.120
A pair of shoes market at Rs.750
A bag market at Rs.250
To learn more about discount refer to:
https://brainly.com/question/1548141
#SPJ1
4) James Madison was born on March
16, 1751. John F. Kennedy was born on
May 29, 1917. If they were both still
alive today, how much older would
James Madison be than John F.
Kennedy?

Answers
Answer:
166 years older.
Step-by-step explanation: Subtract 1751 from 1917
![Find The Missing Side. Round Tothe Nearest Tenth.x928x = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/xloZ7dHEvgULio6a3Ka4eHuMioQgrYoY.png)