Find the mode for the scores: 3,930; 5,300; 8,360; 4,400; 5,350.Select the correct choice below and, if necessary, fill in the answer box to complete your choice.O A. The mode(s) is/are(Use a comma to separate answers as needed.)B. There is no mode.
Answers
The Solution:
Given:
\(3,930,\text{ }5,300,8,360,4,400,5,350.\)Required:
To find the mode of the given data.
Definition:
The mode is the number that occurs most or the number with the highest appearance.
Thus, the data has no mode
Therefore, the correct answer is [option B]
Related Questions
need an answer, please need an answer, please
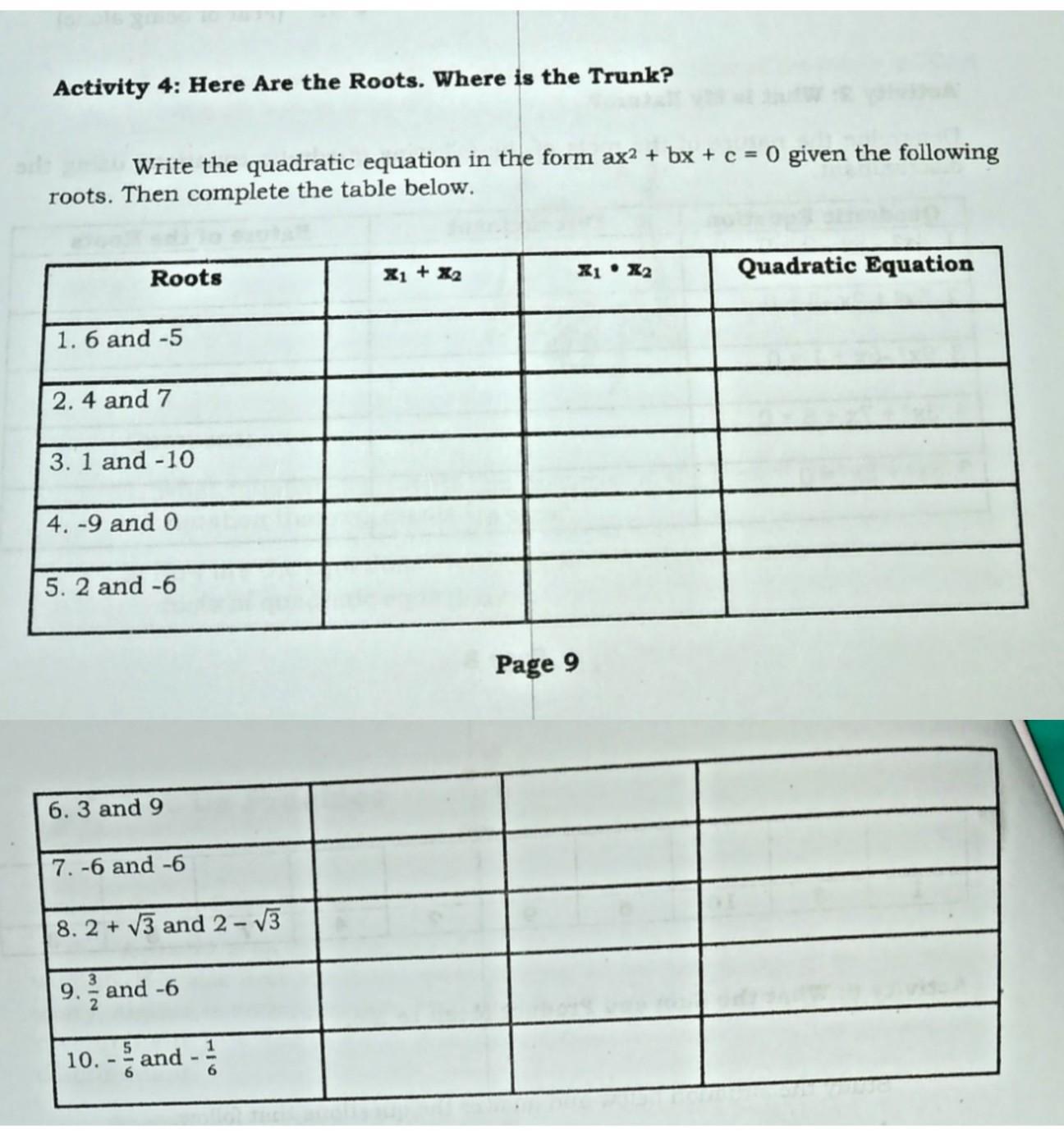
Answers
Answer:
\((x - 6)(x + 5) = {x}^{2} - x - 30 \\ or \\ a {x}^{2} + bx + c\\ {x}^{2} +( x_{1} + x_{2}) x + x_{1} .x_{2} \\ b = x_{1} + x_{2} = 5 - 6 = - 1 \\c = x_{1} .x_{2} = - 6 \times 5 = - 30 \\ \therefore \: {x}^{2} - x - 30\)
you do the rest
Which expression does the model represent?

Answers
—————————————-
The number of students who are enrolled in
math classes at a local college can be
represented by E= -12w+568, where
E represents the math class enrollment at the
college w weeks after the start of the fall
semester.
During which week will the total enrollment be
520 students?
Answers
Answer: 5th week
Step-by-step explanation:
E= -12w+568
520= -12w+568
520+12w=568
12w=48
w=4
4+1=5th week
The yearly Avrage
4. An old furnace cost $850 per year to run. A new one costs $2,500 to buy and will save 34% annually in
energy costs to run it. In how many years will it pay for itself?
Answers
Answer:
9 years
Step-by-step explanation:
To determine the number of years it will take for the new furnace to pay for itself, we need to compare the cost of running the old furnace for that period with the cost of buying and operating the new furnace during the same time.
Let's calculate the cost of running the old furnace for one year:
Old furnace cost per year = $850
Now, let's calculate the savings in energy costs for the new furnace:
Savings in energy costs per year = 34% of $850
= 0.34 * $850
= $289
The total cost of buying and operating the new furnace for one year is:
New furnace cost per year = Cost of buying the new furnace + Savings in energy costs per year
= $2,500 + $289
= $2,789
To find the number of years it will take for the new furnace to pay for itself, we divide the cost of the new furnace by the annual savings:
Number of years to pay for itself = Cost of buying the new furnace / Annual savings
= $2,500 / $289
≈ 8.65
Since we cannot have a fraction of a year, we can round up to the nearest whole number. Therefore, it will take approximately 9 years for the new furnace to pay for itself.
If x = 36 and y = 40 and “x varies directly as y”, then find “x” when y = 80.
Answers
Answer:
x= it will be 76
Question 1 4 pts In the previous lesson, you found the equation of a line to represent the association between latitude and temperature. This is a mathematical model. Use this mathematical model y = -1.07x + 119 predict the average high temperature in September at the following cities that were not included in the original data set: a. Detroit (Lat:42.14) The average high temperature in September will be: OF b. Albuquerque (Lat:35.2) The average high temperature in September will be: OF c. Nome (Lat: 64.5) The average high temperature in September will be: PF d. Peoria, Az (Lat: 33.7) The average high temperature in September will be: OF Question 2 4 pts
Answers
ANSWER:
a. 73.91 °F
b. 81.34 °F
c. 49.99 °F
d. 82.94 °F
STEP-BY-STEP EXPLANATION:
We have the following mathematical model that predicts the temperature depending on the latitude:
\(\begin{gathered} y=-1.07x+119 \\ \text{where x is the latitude and y is the temperature} \end{gathered}\)Therefore:
a.
\(\begin{gathered} y=-1.07\cdot42.14+119 \\ y=73.91 \end{gathered}\)b.
\(\begin{gathered} y=-1.07\cdot35.2+119 \\ y=81.34 \end{gathered}\)c.
\(\begin{gathered} y=-1.07\cdot64.5+119 \\ y=49.99 \end{gathered}\)d.
\(\begin{gathered} y=-1.07\cdot33.7+119 \\ y=82.94 \end{gathered}\)What is a good practice to remember when adding transitions to a presentation?
Answers
A good practice to remember when adding transitions to a presentation is to ensure that they are purposeful, consistent, and enhance the overall flow of the presentation.
Purposeful: Use transitions to guide the audience through your key points and ideas, making sure they complement the content and contribute to the overall message.
Consistent: Maintain a consistent style of transitions throughout your presentation to maintain a cohesive look and feel. Avoid using too many different types of transitions, as this may be distracting.
Enhance flow: Transitions should help create a smooth flow between slides and ideas, making it easy for the audience to follow your presentation. Avoid using abrupt or overly flashy transitions that may interrupt the natural progression of your content.
finally, Test your presentation with the transitions to make sure they enhance the overall flow and comprehension of your message.
for such more question on overall flow
https://brainly.com/question/10922478
#SPJ11
Bro
I’m lazy and I don’t wanna do it if someone can do it it would mean a lot

Answers
Answer:
Option 2.
Step-by-step explanation:
X is a number greater than the equality. Therefore the arrow will go to the bigger side. It also is not equal to the equality hence the cirle is open.
Answer:
I feel ya. It's the second one. Have a nice day.
Step-by-step explanation:
Amadi is three times as old as Chima. The sum of their ages is 24
Answers
Answer:
Amadi: 20 years old
Chima : 4 years old
Find the value of y when x=2 y=1/7(x+5)
Answers
Answer:
y = 1
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightStep-by-step explanation:
Step 1: Define
y = 1/7(x + 5)
x = 2
Step 2: Evaluate
Substitute in x: y = 1/7(2 + 5)(Parenthesis) Add: y = 1/7(7)Multiply: y = 1PLEASE HELP ME! I DONT HAVE LONG

Answers
Answer:
d
Step-by-step explanation:
you multiply them then you divide by 2
Find the y-intercept for the parabola defined by
this equation:
y=-4x^2-x+3
Answers
Answer:
y is 0,3
Step-by-step explanation:
To find the x-intercept, substitute in
0
for
y
and solve for
x
. To find the y-intercept, substitute in
0
for
x
Answer:
(0,3)
Step-by-step explanation:
Two methods:
Method 1: General method for any equation
Method 2: Method specific for parabolas in standard form
Method 1: General method for any equation
For any two-variable equation to be graphed, the y-intercept is the point where the graph crosses the y-axis. The y-axis is a vertical line through the origin (0,0).
Any y-intercept is on that line, and to get to that point starting from the origin, one can't travel left or right to get to the y-intercept point (without moving back to the y-axis). The only movement would be up or down.
Since no left-right movement will happen, the x-coordinate is zero.
For any two-variable equation, the x and y coordinates of any point on the graph are linked by the equation. If it is known that the x-value is zero, the y-value associated with that x-value is given by substituting zero into the equation everywhere there is an "x", and solving for "y".
\(y=-4x^2-x+3\)
\(y=-4(0)^2-(0)+3\)
Order of operations requires exponents before multiplication, or addition & subtraction...
\(y=-4(0)-(0)+3\)
multiplication...
\(y=0-0+3\)
addition & subtraction, from left to right...
\(y=3\)
So, when the x-value is zero, the y-value is three. Therefore, the ordered pair representing that point is (0,3).
Method 2: Method specific for parabolas in standard form
The given equation is the equation for a parabola (as stated in the question), and it is given in "standard form": \(y=ax^2+bx+c\), where a, b, and c are real numbers (and a isn't equal to zero, because then the x-squared term would be zero, and the equation would really just be a linear equation).
Note that for our equation, it is in standard form if we rewrite the equation to only use addition, \(y=-4x^2+-1x+3\), where \(a=-4, ~b=-1 ~ \text{and}~c=3\)
For a parabola in standard form, the y-intercept is always at a height of "c".
So, the y-intercept would be (0,3).
How to get the Index result in excel
Answers
To get the index result in an Excel spreadsheet, you can use the INDEX function.
How can INDEX function be used to get index result?The INDEX function in Excel allows you to retrieve a value from a specific location within an array or range. By providing the array/range and the row and column numbers, you can extract the desired value.
For example, if you want to retrieve the value from the third row and second column of a range, you will use formula "=INDEX(A1:D5, 3, 2)". This will return the value at that specific location in the range. You will adjust row and column numbers based on needs to obtain the desired index result in Excel.
Read more about INDEX function
brainly.com/question/28488081
#SPJ1
Annette has 3 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same distance to cool down. If she runs at a speed of 9mph and walks back at a speed of 3mph , how long should she plan to spend walking back?
Answers
Answer:
Annette should plan to spend 2.25 hours walking back.
Step-by-step explanation:
To solve this problem, we can use the formula:
Time = Distance / Speed
Let's assume the distance of the race is D miles.
Annette spends her time running the distance of the race, which takes:
Time running = D / 9 hours
She then walks back the same distance, which we need to find the time for:
Time walking = D / 3 hours
Since Annette has a total of 3 hours for her training, the sum of the running time and walking time should equal 3 hours:
D / 9 + D / 3 = 3
To simplify the equation, we can multiply all terms by 9 to eliminate the denominators:
D + 3D = 27
Combining like terms:
4D = 27
Dividing both sides of the equation by 4:
D = 6.75
So, the distance of the race is 6.75 miles.
To find the time Annette should spend walking back, we substitute the distance into the time-walking formula:
Time walking = D / 3 = 6.75 / 3 = 2.25 hours
Therefore, Annette should plan to spend 2.25 hours walking back.
A type of dragon fly is the fastest insect. a. Write an equation to find how far the dragonfly can travelb. Use the equation to determine how far the dragon fly can travel in one minute
Answers
A type of dragonfly is the fastest insect.
a. Write an equation to find how far the dragonfly can travel
d = Distance Traveled (
s = Time in second
For calculating the expression, we are gonna use this two
points
A = (1, 23)
B = (5, 115)
First, we are going to calculate the slope
\(\begin{gathered} m=\frac{115-23}{5-1} \\ m=\frac{92}{4} \\ \\ m=23 \end{gathered}\)Now, we are going to calculate the intercept
\(\begin{gathered} b=y-mx \\ b=23-23\cdot1 \\ b=0 \end{gathered}\)The equation would be
\(y=23x\)Using our nomenclature
\(d=23\cdot s\)b. Use the equation to determine how far the dragonfly can travel in one minute
one minute = 60 seconds
\(\begin{gathered} d=23\cdot60s \\ d=1380 \end{gathered}\)Solve for t.
-3t + 3 – 7t = -90 – 7
Answers
Answer:
t = 10Step-by-step explanation:
-3t + 3 - 7t = -90 - 7
Simplify both sides of the equation
That's
- 10t + 3 = - 97
Using the subtraction property subtract 3 from both sides of the equation
We have
- 10t + 3 - 3 = -97 - 3
- 10t = - 100
Divide both sides by - 10
\( \frac{ - 10t}{ - 10} = \frac{ - 100}{ - 10} \)
We have the final answer as
t = 10Hope this helps you
Answer:
Step-by-step explanation:
-3t + 3 - 7t = -90 - 7
-10t + 3 = -97
-10t = -100
t = 10
Robert had 2 2/5 cups of chocolate syrup left in his freezer he used 1/4 cup of Chocolate syrup when he makes a milkshake what is the maximum number of milkshakes that Robert can make with the chocolate syrup

Answers
Robert can make a maximum of 8 milkshakes with the remaining chocolate syrup.
How to find the maximum number of milkshakes that Robert can make with the chocolate syrupConverting the mixed number 2 2/5 to an improper fraction: 2 2/5 = 12/5
Subtracting the amount of chocolate syrup used per milkshake from the total amount of chocolate syrup:
12/5 - 1/4 = (48 - 5) / 20 = 43/20
Therefore, Robert has 43/20 cups of chocolate syrup left, which is the maximum amount he can use to make milkshakes.
For maximum number of milkshakes:
(43/20) / (1/4) = (43/20) x (4/1) = 172/20 = 8.6
Since Robert cannot make a fraction of a milkshake, he can make a maximum of 8 milkshakes with the remaining chocolate syrup.
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
Explain why 1/12+ 1/12+ 1/12is the same as 1/4.
Answers
Answer:
1/4 = 3/12 = 1/12+1/12+1/12
Step-by-step explanation:
Because 1/4 equals 3/12.
Wesley walked 11 miles in 4
hours.
If he walked the same distance every hour,
how far did he walk in one hour?
Write your answer:
Using a whole number of miles and a whole number of feet
Answers
Answer:
3 miles
58080 feet
Step-by-step explanation:
please help!! need it fast, will give brainliest!! and pls show work !!
Find the measure of angle AEB

Answers
Answer:
An acute angle
Step-by-step explanation:
An acute angle is smaller than an obtuse ad right angle.
hope this helps and hope it was right 'cause I really don't know what you meant. :)
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
89 to the nearest 10
Answers
Answer:
it is : 90
Step-by-step explanation:
Answer:
90
Step-by-step explanation:
anything under 5 goes down
anything above 5 goes up
89 is above 85, so it's gonna be 90
2/5 of 1 meter=____cm
Plz help thx
Answers
Answer:
40 cm
Explanation:
2/5 = 0.4
1 meter = 100 cm
so,
100 x 0.4= 40 cm
Hence, Solve the equation
X Х
1- x
4x=
Answers
A man pulled a cart filled with stones that had a total mass of 60 kg.
He increased the amount of force used to pull the cart from 60 N to 90 N, what is the new
acceleration of the cart?
Answers
a1 = f/m
a1 = 60/60 = 1ms^-2
a2 = f2/m
a2 = 90/60
a2 = 1.5ms^-2
The amount of force used to pull the cart from 60 N to 90 N, the new acceleration of the cart is, 1.5 m/s²
What is Force ?The definition of force is the pushing or pulling of anything. Push and pull are the result of two things interacting with one another. Stretch and crush are two more phrases that can be used to describe force.
Formula of force,
F = ma
Given that,
A man pulled a cart filled with stones that had a total mass of 60 kg
He increased the amount of force used to pull the cart from 60 N to 90 N
New acceleration of cart = ?
F = ma
Old acceleration,
60 = 60a
a = 1 m/s²
New acceleration,
90 = 60a
a = 90/60
a = 3/2
a = 1.5 m/s²
Hence, the new acceleration is 1.5 m/s²
To know more about Force check:
https://brainly.com/question/13191643
#SPJ2
If ✓(x+iy) =a+ib, then find ✓(x-iy) and x^2+y^2.
Answers
The values of the complex expressions are ✓(x - iy) = a - ib and x² + y² = (a + ib)²(a - ib)²
Calculating the complex expressionsFrom the question, we have the following parameters that can be used in our computation:
✓(x + iy) = a + ib
Changing the signs, we have
✓(x - iy) = a - ib
Multiply both expressions
This gives
✓(x + iy) * ✓(x - iy) = (a + ib)(a - ib)
Square both sides
So, we have
(x + iy) * (x - iy) = (a + ib)²(a - ib)²
This gives
x² + y² = (a + ib)²(a - ib)²
Hence, the values of ✓(x - iy) is a - ib and x² + y² is (a + ib)²(a - ib)²
Read more about complex expressions at
https://brainly.com/question/10662770
#SPJ1
sally bought the pizza shown above for lunch which was cut into 10 equal slices what percentage of the pizza did sally and her friend eat if they ate three pieces
Answers
Answer:
30% of the pizza was eaten
Step-by-step explanation:
10 pieces = 100%
they ate 3 soooo 30%
Answer:
90%
Step-by-step explanation:
tanx(1+cos2x)=sin2x prove the identity
Answers
Using double angle identity, we are able to prove tan(x)(1 + cos(2x)) = sin(2x).
What is the prove of the given identity?To prove the identity tan(x)(1 + cos(2x)) = sin(2x), we can start by using trigonometric identities to simplify both sides of the equation.
Starting with the left-hand side (LHS):
tan(x)(1 + cos(2x))
We know that tan(x) = sin(x) / cos(x) and that cos(2x) = cos²(x) - sin²(x). Substituting these values, we get:
LHS = (sin(x) / cos(x))(1 + cos²(x) - sin²(x))
Next, we can simplify the expression by expanding and combining like terms:
LHS = sin(x) / cos(x) + sin(x)cos²(x) / cos(x) - sin³(x) / cos(x)
Simplifying further:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
Now, let's work on the right-hand side (RHS):
sin(2x)
Using the double angle identity for sine, sin(2x) = 2sin(x)cos(x).
Now, let's compare the LHS and RHS expressions:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
RHS = 2sin(x)cos(x)
To prove the identity, we need to show that the LHS expression is equal to the RHS expression. We can combine the terms on the LHS to get a common denominator:
LHS = [sin(x) - sin³(x) + sin(x)cos²(x)] / cos(x)
Now, using the identity sin²(x) = 1 - cos²(x), we can rewrite the numerator:
LHS = [sin(x) - sin³(x) + sin(x)(1 - sin²(x))] / cos(x)
= [sin(x) - sin³(x) + sin(x) - sin³(x)] / cos(x)
= 2sin(x) - 2sin³(x) / cos(x)
Now, using the identity 2sin(x) = sin(2x), we can simplify further:
LHS = sin(2x) - 2sin³(x) / cos(x)
Comparing this with the RHS expression, we see that LHS = RHS, proving the identity.
Learn more on trigonometric identity here;
https://brainly.com/question/24496175
#SPJ1
After flooding damaged much of the crop, the cost of a head of lettuce jumped from $0.92 to $2.26. What percent of increase is this? Round to the nearest one percent.
Answers
Answer:
146%
Step-by-step explanation:
\( percent~change = \dfrac{new~price - old~price}{old~price} \times 100% \)
If the percent change is positive, it is a percent increase.
If the percent change is negative, it is a percent decrease.
Your numbers are
old price = $0.92
new price = $2.26
Plug in the numbers in the formula above and evaluate the expression.
percent change = ($2.26 - $0.92)/($0.92) * 100%
percent change = ($1.34)/($0.92) * 100%
percent change = 1.4565 * 100%
percent change = 146%
Since the percent change is a positive number, it is a percent increase.
Answer: The percent increase is 146%.
Find the sum of the first 27 terms
of the arithmetic sequence.
First, fill in the equation.
a₁
= 5 and a27
Sn = 2/(a₁ + an)
Sn
=
[?]
2
+
=
83

Answers
Answer:
S₂₇ = 1188
Step-by-step explanation:
using the given formula for \(S_{n}\) , that is
\(S_{n}\) = \(\frac{n}{2}\) (a₁ + \(a_{n}\) )
with a₁ = 5 and \(a_{n}\) = a₂₇ = 83 , then
S₂₇ = \(\frac{27}{2}\) (5 + 83) = 13.5 × 88 = 1188