find the ninth term of the sequence if the second term is 12 and the fourth term is 16/3.
Answers
with the assumption this is a geometric sequence and thus it as an "r" common ratio, so we know that the 3rd term must be 12 * r and the 4th term must be 12 * r * r, so let's make a quick table
\(\begin{array}{rll} term&value\\ \cline{1-2} a_2&12\\ a_3&12\cdot r\\\cline{1-2} a_4&(12\cdot r)r\\ &12r^2\\ &\frac{16}{3}\\\cline{1-2} a_5&12r^3\\ a_6&12r^4\\ a_7&12r^5\\ a_8&12r^6\\ a_9&12r^7 \end{array}\qquad \implies \begin{array}{llll} 12r^2=\cfrac{16}{3}\implies r^2=\cfrac{16}{12\cdot 3}\implies r^2=\cfrac{4}{9}\\\\\\ r=\sqrt{\cfrac{4}{9}}\implies r=\cfrac{\sqrt{4}}{\sqrt{9}}\implies r=\cfrac{2}{3} \end{array} \\\\[-0.35em] ~\dotfill\)
\(a_9=12\left( \cfrac{2}{3} \right)^7\implies a_9=12\cdot \cfrac{128}{2187}\implies a_9=\cfrac{512}{729}\)
Related Questions
Classify the trios of sides as acute, obtuse, or right triangles.

Answers
The triangles with the given side lengths are classified as follows:
Acute: 27, 36, 46, \(6, \sqrt{61}, \sqrt{96}\)Right: \(\sqrt{6}, 6, \sqrt{42}\), \(\sqrt{23}, 7, \sqrt{72}\), 7, 24, 25, 15, 20, 25.Obtuse:How to classify the triangles?The ordered side lengths of the triangles are given as follows:
a, b and c.
Considering these side lengths, the triangles are classified as follows:
Acute if a² + b² > c².Right if a² + b² = c².Obtuse if a² + b² < c².More can be learned about triangles at https://brainly.com/question/1058720
#SPJ1
1 1. Determine if the series (-1)*4k converges or diverges. If it converges k=1 5k - 1 approximate the sum S of the series to within 0.01. (5 pts) +1 -(-1)"+1 Determine if the series converges absolutely, converges conditionally, or n=1 vn diverges.
Answers
The given series is (-1)^n * (4n) with n starting from 1. To determine if the series converges or diverges, we can use the Alternating Series Test. For an alternating series, it converges if:
1. The terms are non-increasing: a_n+1 <= a_n for all n.
2. The limit of the terms as n goes to infinity is 0: lim(n→∞) a_n = 0.
The terms a_n = 4n are increasing and not non-increasing, so the series diverges. Thus, we cannot approximate the sum S of the series to within 0.01.
For the second part of the question, we check the absolute convergence by considering the series with absolute values of the terms: Σ(4n) with n starting from 1. This is a divergent arithmetic series, so the original series does not converge absolutely. Since the original series also diverges, we conclude that the series diverges.
The given series is (-1)*4k. To determine if it converges or diverges, we need to check if its terms approach zero as k goes to infinity. Since the absolute value of each term is 4k, which increases without bound as k goes to infinity, the series diverges.
Next, if we assume k=1 5k - 1 and sum the first few terms of the series, we get:
S = (-1)*4(1) + (-1)*4(2) + (-1)*4(3) + (-1)*4(4) + (-1)*4(5) + (-1)*4(6) + ...
S = -4 -8 -12 -16 -20 -24 -...
We can see that the sum of the series is -4 times the sum of the positive integers, which is a well-known formula with the value of -1/12. Therefore, the sum of the given series is 1/3.
Finally, to determine if the series converges absolutely, converges conditionally, or diverges, we need to check if the absolute value of each term of the series converges or diverges. Since the absolute value of each term is 4k, which increases without bound as k goes to infinity, the series diverges. Therefore, the series converges conditionally.
Learn more about Converges:
brainly.com/question/9385279
#SPJ11
7y+5y-3y= How would I simplify this?
Answers
Answer:
9y
Step-by-step explanation:
Add 7y and 5y which equals 12y. Then subtract 3y from 12y and u get 9y. It might be wrong
Let's simplify step-by-step.
7
y
+
5
y
−
3
y
=
7
y
+
5
y
+
−
3
y
Combine Like Terms:
=
7
y
+
5
y
+
−
3
y
=
(
7
y
+
5
y
+
−
3
y
)
=
9
y
help please!!! So confused.I thought I got them right but when go to to type in my answer they're wrong.


Answers
Answer:
i can't see it
Step-by-step explanation:
2) Ashton left his house and ran 4 miles east and then 3 miles north. He then took the diagnol path back home. If he burned 105 calories every mile that he ran, how many total calories did he burn on his run? (just type in the number value and units)
Answers
1,470
Step-by-step explanation:
because if he 4 miles and than 3 miles you would add them and get 7. you would take that 7 and double the 7 and multiply it by 105 cause that's how many calories he burnt each miles he ran then you would get the total of 1470 calories
You are at a rate of pay for $24.00/hour. You work a 32 hour work week. What is your gross pay?
Answers
What is the residual for observation 6? Observation Actual Demand (A) Forecast (F) 1 35 --- 2 30 35 3 26 30 4 34 26 5 28 34 6 38 28 Group of answer choices .20 Cannot be determined based on the given information. 10 -6
Answers
To calculate the residual for observation 6, we first need to find the forecast for observation 6. Based on the given information, the forecast for observation 6 is 34. Therefore, the residual for observation 6 would be:
Residual = Actual Demand - Forecast
Residual = 38 - 34
Residual = 4
So the residual for observation 6 is 4.
Hi! To find the residual for observation 6, we need to subtract the forecast (F) from the actual demand (A). In this case, the observation 6 values are:
Actual Demand (A): 38
Forecast (F): 28
Now, we'll calculate the residual:
Residual = Actual Demand (A) - Forecast (F)
Residual = 38 - 28
Residual = 10
So, the residual for observation 6 is 10.
(Second Isomorphism Theorem) If K is a subgroup of G and N is a normal subgroup of G, prove that K/(K ∩ N) is isomorphic to KN/N
Answers
We use the First Isomorphism Theorem to show that K/(K ∩ N) is isomorphic to the image of φ, which is φ(K) = {kN | k is in K}. Since φ is a homomorphism, φ(K) is a subgroup of KN/N. Moreover, φ is onto, meaning that every element of KN/N is in the image of φ. Therefore, by the First Isomorphism Theorem, K/(K ∩ N) is isomorphic to KN/N, completing the proof of the Second Isomorphism Theorem.
To prove the Second Isomorphism Theorem, we need to show that K/(K ∩ N) is isomorphic to KN/N, where K is a subgroup of G and N is a normal subgroup of G.
First, we define a homomorphism φ: K → KN/N by φ(k) = kN, where kN is the coset of k in KN/N. We need to show that φ is well-defined, meaning that if k1 and k2 are in the same coset of K ∩ N, then φ(k1) = φ(k2). This is true because if k1 and k2 are in the same coset of K ∩ N, then k1n = k2 for some n in N. Then φ(k1) = k1N = k1nn⁻¹N = k2N = φ(k2), showing that φ is well-defined.
Next, we show that φ is a homomorphism. Let k1 and k2 be elements of K. Then φ(k1k2) = k1k2N = k1Nk2N = φ(k1)φ(k2), showing that φ is a homomorphism.
Now we show that the kernel of φ is K ∩ N. Let k be an element of K. Then φ(k) = kN = N if and only if k is in N. Therefore, k is in the kernel of φ if and only if k is in K ∩ N, showing that the kernel of φ is K ∩ N.
For such more questions on Isomorphism Theorem:
https://brainly.com/question/31227801
#SPJ11
Can you guys help me find the slope for the given graph and y-intercept
(pictures included)

Answers
Answer:
I believe the answer is
\(y = \frac{2}{3} x + 1\)
slope = 2/3x
y-intercept = 1
Step-by-step explanation:
Hope this helps!
Find the circumference of the circle (use 3. 14 for pi). Show your work. Round to the nearest tenth.
Answers
The circumference of the circle is C = 144.44 yd .
From the given figure :
we observe that the radius r = 23 yd
we know that ,
What is circumference of circle ?
Circumference is the distance around the perimeter of a circle. It is calculated by multiplying the distance across the center .
A circle's perimeter is known as its circumference.
Formula :
C = 2πr
= 2 * 3.14 * 23
= 46 * 3.14
= 46 * 314 / 100
= 14444 / 100
= 144.44 yd
Hence the circumference of the circle is 144.44 yd .
Learn more about the circle here:
https://brainly.com/question/11833983
#SPJ4
Full question :
is in the image uploaded

Four less than x = ??
Answers
Answer:
x-4
Step-by-step explanation:
Answer:
x-4
Step-by-step explanation:
If you know this could you help me?
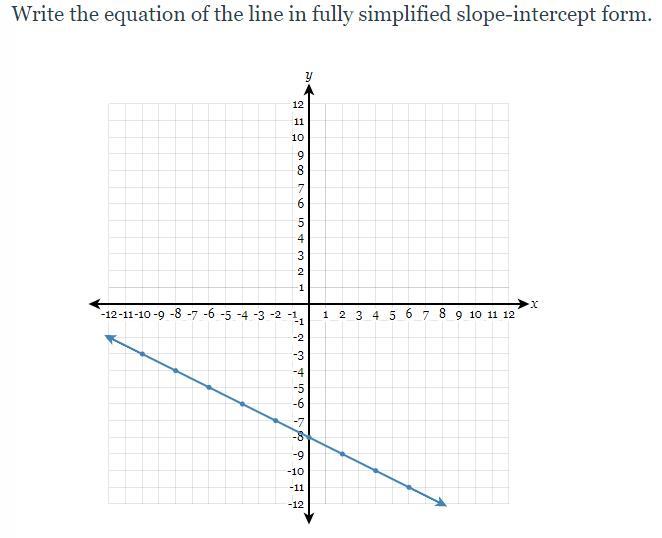
Answers
Answer:
Equation : y = -0.5x − 8
Step-by-step explanation:
because i grabbed two points and plugged them in im not very good at explaining but im 99% sure thats right
If u lv and || 2 || = 1, || 0 || = 3, then (2u - 30). (3u + 2x) (a) -8 (6) -48 (€) -12 (d) 24 (e) none of these
Answers
The dot product of the vectors is -126 ± 4√7, which is none of the given options. The correct answer is (e)
The dot product of two vectors is given by the sum of the products of their corresponding components. So, we have: (2u - 30) · (3u + 2x) = 6u · u + 4x · u - 90u · 1 + 2x · (-15)
Since ||u|| = 1, we have u · u = ||u||² = 1² = 1. Also, we are given that ||0|| = 3, which means that x · x = ||x||² = 3² = 9. Substituting these values, we get:
(2u - 30) · (3u + 2x) = 6 + 4x - 90 + 2(-15)
= 6 + 4x - 90 - 30
= -114 + 4x
We can now find x using the fact that ||2|| = 1:
||2u - 30||² = (2u - 30) · (2u - 30) = 4u · u - 120u · 1 + 900
= 4 - 120 + 900 = 784
Taking the square root of both sides, we get:
||2u - 30|| = 28
Therefore, we have:
||3u + 2x||² = (3u + 2x) · (3u + 2x) = 9u · u + 12x · u + 4x · 3u + 4x · 2x
= 9 + 12x + 12x + 4x² = 9 + 24x + 4x²
And since ||3u + 2x|| = ||2|| = 1, we have:
||3u + 2x||² = 1² = 1
Substituting this expression and simplifying, we get:
9 + 24x + 4x² = 1
4x² + 24x + 8 = 0
x² + 6x + 2 = 0
Using the quadratic formula, we find:
x = (-6 ± √(6² - 4(1)(2))) / 2(1) = (-6 ± √28) / 2 = -3 ± √7
Therefore, we have:
(2u - 30) · (3u + 2x) = -114 + 4x
= -114 + 4(-3 ± √7)
= -126 ± 4√7
Since none of the answer choices match this expression, the correct answer is (e) none of these.
To know more about dot product, refer here:
https://brainly.com/question/29097076#
#SPJ11
Luca has already cycled 5 kilometers this year, plus he plans to cycle 5 kilometers during each trip to work. How many trips will Luca make to cycle a total of 50 kilometers?
Answers
Lucas rode 1,000 meters b/c
2 klm is = to 2000 meters.
and 1/4 of 2000 meters is 500 meters but then he had
to turn back to go home so that's another 500 meters and in total he rode 1,000 meters. give brainleist
for a brainlist and +10 points
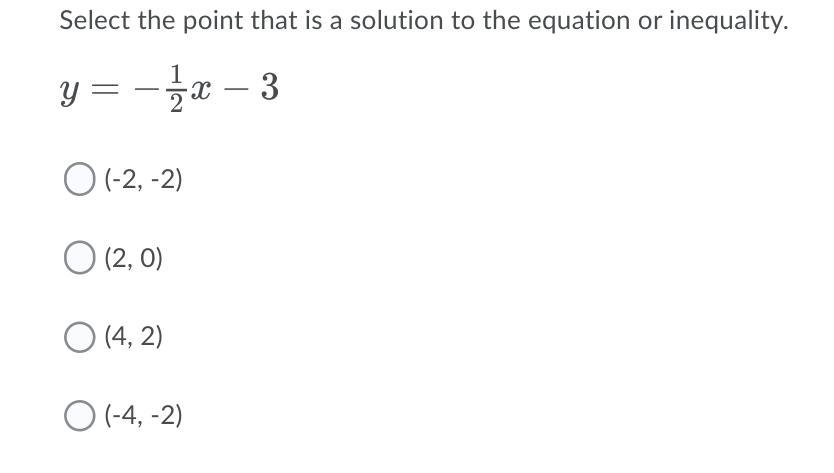
Answers
Answer:
(- 2, - 2 )
Step-by-step explanation:
Substitute the x- coordinate of the points into the equation and if the value obtained is equal to the y- coordinate of the point then it is a solution.
(- 2, - 2 ) → y = - \(\frac{1}{2}\) (- 2) - 3 = 1 - 3 = - 2 ← same as y- coordinate
(2, 0 ) → y = - \(\frac{1}{2}\) (2) - 3 = - 1 - 3 = - 4 ≠ 0 ← not a solution
(4, 2 ) → y = - \(\frac{1}{2}\) (4) - 3 = - 2 - 3 = - 5 ≠ 2 ← not a solution
(- 4, - 2 ) → y = - \(\frac{1}{2}\) (- 4) - 3 = 2 - 3 = - 1 ≠ - 2 ← not a solution
Write the term that contains A^6 in the binomial expansion of (A + 3B)^10
Answers
The term which contains A⁶ in the given binomial expansion as required to be determined is; 17010A⁶B⁴.
Which term contains A⁶ in the binomial expansion?It follows from the task content that the term which contains A⁶ in the binomial expansion is to be determined.
From binomial expansions; the term containing A⁶ in the expansion would be the fifth term and it's coefficient would be; ¹⁰C⁴ = 210.
Therefore, the term would be; 210 (A)⁶ (3B)⁴.
= 210A⁶ • 81B⁴
= 17010A⁶B⁴.
Ultimately, the term that contains A⁶ in the binomial expansion is; 17,010A⁶B⁴.
Read more on binomial expansion;
https://brainly.com/question/13602562
#SPJ1
eric walks around a man-made circular lake (pictured above) four times. how far (in miles) has he walked? eric has walked a total of
Answers
Eric would have walked 12.56636 miles in total. You will need to plug in the actual radius of the lake to find the precise distance he walked.
To calculate the distance Eric has walked around the man-made circular lake, we need to know the circumference of the lake and then multiply it by the number of times he walked around it. The circumference of a circle is given by the formula C = 2πr, where C is the circumference, π (pi) is approximately 3.14159, and r is the radius of the circle. However, since the image of the circular lake is not provided, I cannot determine its radius.
Once you have the radius of the lake, you can use the formula to find the circumference. Then, multiply the circumference by four to account for Eric walking around the lake four times. If the result is in a different unit of measurement (e.g., feet, yards), convert it to miles by using the appropriate conversion factor.
For example, if the radius of the lake is 0.5 miles, the circumference would be:
C = 2 × 3.14159 × 0.5 = 3.14159 miles
Since Eric walks around the lake four times, the total distance he walks would be:
Total Distance = 3.14159 × 4 = 12.56636 miles
Learn more about radius here :-
https://brainly.com/question/12922563
#SPJ11
A toy rocket is launched from a 5.6 m high platform in such a way that its height, h (in meters), after t seconds is given by the equation h= - 4.97t^2+ 38.5t + 5.6. How long will it take for the rocket to hit the ground?
Answers
The toy rocket will hit the ground after approximately 3.86 seconds.
Calculating time for toy rocket to reach groundThe rocket will hit the ground when its height is equal to zero, so we can use the equation h = -4.97t^2 + 38.5t + 5.6 to find the value of t that satisfies this condition. To do this, we set h equal to zero and solve for t:
0 = -4.97t^2 + 38.5t + 5.6
-5.6 = -4.97t^2 + 38.5t
4.97t^2 - 38.5t - 5.6 = 0
This is a quadratic equation and can be solved using the quadratic formula:
t = (-b ± √(b^2 - 4ac)) / (2a)
Where a = 4.97, b = -38.5, and c = -5.6.
Plugging in these values, we get:
t = (-(-38.5) ± √((-38.5)^2 - 4 * 4.97 * -5.6)) / (2 * 4.97)
t = (38.5 ± √(1466.25 + 113.92)) / 9.94
t = (38.5 ± √1580.17) / 9.94
The square root of 1580.17 is 39.67, so:
t = (38.5 ± 39.67) / 9.94
t = (38.5 + 39.67) / 9.94 or (38.5 - 39.67) / 9.94
The first solution gives us a time of approximately 3.86 seconds, while the second solution is negative and therefore represents an unrealistic result.
The toy rocket will hit the ground after approximately 3.86 seconds.
Learn more on quadratic equation: https://brainly.com/question/20038608
#SPJ1
Help please
Multiply.
-2w(-5-w)
Answers
Answer:
\(10w + 2w^{2}\)
Step-by-step explanation:
To solve this, we have to apply the distributive property and simplify:
(-2w x -5) + (-2w x -w)
\(10w + 2w^{2}\)
Answer:
\(10w + 2w {}^{2} \)
Please hurry
Add using a number line.
−25+45
Drag and drop the word SUM to the correct value on the number line.

Answers
Answer: i got it
Step-by-step explanation:
i hope this helped

Given the expression 10x2-18x-4
Part A: what is the greatest common factor? Explain how to find it.
Part B: Factor the expression completely. Show all necessary steps.
Part C: Check your factoring from Part B by multiplying. Show all necessary steps.
Help !!!!!
Answers
If the expression is 10x2-18x-4.:
a. The greatest common factor of the expression 10x^2 - 18x - 4 is 2.
b. The expression 10x^2 - 18x - 4 can be factored completely as: 10x^2 - 18x - 4 = 2(5x + 1)(x - 2)
C. the factoring from Part B is correct.
How to find the greatest common factor?Part A: To find the greatest common factor of the expression 10x^2 - 18x - 4, we need to find the largest factor that divides all three terms of the expression evenly. One way to do this is to factor out the greatest common factor using the distributive property.
10x^2 - 18x - 4 = 2(5x^2 - 9x - 2)
Now, we need to factor the expression inside the parentheses further to see if we can find any additional common factors.
5x^2 - 9x - 2 can be factored using the quadratic formula, but it does not have any common factors other than 1.
Therefore, the greatest common factor of the expression 10x^2 - 18x - 4 is 2.
Part B: To factor the expression completely, we can start by using the greatest common factor of 2.
10x^2 - 18x - 4 = 2(5x^2 - 9x - 2)
Next, we need to factor the expression 5x^2 - 9x - 2 further. We can use the factoring method of product and sum:
The product of 5 and -2 is -10, and the sum of the factors that multiply to -10 and add to -9 is -10 and 1.
So, we can write 5x^2 - 9x - 2 as:
5x^2 - 10x + x - 2
= 5x(x - 2) + 1(x - 2)
= (5x + 1)(x - 2)
Therefore, the expression 10x^2 - 18x - 4 can be factored completely as:
10x^2 - 18x - 4 = 2(5x + 1)(x - 2)
Part C: To check our factoring from Part B, we can multiply the factors using the distributive property and simplify:
2(5x + 1)(x - 2) = 2(5x)(x) + 2(5x)(-2) + 2(1)(x) + 2(1)(-2)
= 10x^2 - 20x + 2x - 4
= 10x^2 - 18x - 4
Therefore, the factoring from Part B is correct.
Learn more about greatest common factor here:https://brainly.com/question/219464
#SPJ1
pls pls pls pls pls help

Answers
Answer:
\(y=\frac{1}{2}\)
Step-by-step explanation:
\(4(y+1)= \frac{3}{1-y}\)
\(4y+4= \frac{3}{1-y}\)
\((4y+4)(1-y)= 3\)
\(4y(1-y)+4(1-y)=3\)
\(4y-4y^{2} +4-4y=3\)
\(-4y^{2}=3-4\)
\(4y^{2}=1\)
\(y^{2} = \frac{1}{4}\)
\(y=\sqrt{\frac{1}{4} }\)
\(y=\frac{1}{2}\)
Use the information given to enter an equation in standard form.
Slope is 6, and (1, 8) is on the line.
Answers
Answer:
y=6x+2
Step-by-step explanation:
y=mx+c
8=6(1)+c
8=6+c
c=2
y=6x+2
vIn 2001, the moose population in a park was measured to be 4,860. By 2009, the population was measured again and was found to be 5,900. Assume the population continues to change linearly. vFind a foula for the moose population, P, since 2001.
Answers
The formula for the moose population P since 2001 is P(t) = 340t + 4860. This means that the population has been increasing linearly at a rate of 340 moose per year since 2001.
The slope of the line can be found by taking the difference in the y-values over the difference in the x-values: (5900 - 4860) / (2009 - 2001) = 1040 / 8 = 130. This tells us that the population has been increasing by an average of 130 moose per year between 2001 and 2009.
To find the y-intercept of the line, we can use the point-slope form of a line: y - y1 = m(x - x1), where (x1, y1) is any point on the line and m is the slope. We can use the point (2001, 4860) since we know that the population was 4860 in 2001. Plugging in the values, we get: P - 4860 = 130(t - 2001).
Simplifying, we get the formula for the moose population P since 2001: P(t) = 130t + 4860. However, the problem asks for the formula to be in terms of the number of years since 2001, not the actual year. To do this, we can subtract 2001 from t: P(t) = 130(t - 2001) + 4860.
Simplifying further, we get: P(t) = 130t - 147070. However, this formula gives the population for any year since 2001, including decimals. To find the formula for whole numbers of years since 2001, we can round down the value of t to the nearest whole number. This gives us the final formula: P(t) = 340t + 4860, where t is the number of whole years since 2001.
To know more about linear equation refer here:
https://brainly.com/question/32634451
#SPJ11
determine the equation of the circle graphed below
( help please )

Answers
9514 1404 393
Answer:
(x +2)^2 +(y -5)^2 = 9
Step-by-step explanation:
The circle shown has a radius of r = 3 and a center at (h, k) = (-2, 5).
The equation of a circle is ...
(x -h)^2 +(y -k)^2 = r^2
For the given center and radius, the equation is ...
(x +2)^2 +(y -5)^2 = 9
can you help me with the question pls it's about standard form/scientific notation.
I'm confused with the minuses on the indices.
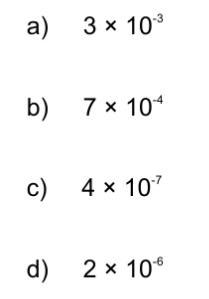
Answers
Answer:
-3 squared means it is 0.1 for each -1, so it would be 0.001
Step-by-step explanation:
it is 0.003 for a and the rest you can figure out
please help me!!
basic Radicals

Answers
Answer:
C)
Step-by-step explanation:
\(x = \frac{\sqrt{a}}{ \sqrt{b}} = \sqrt{\frac{a}{b}}\\\\\)
Both sides take square
\(x^{2}= ( \sqrt{\frac{a}{b}})^{2}=\frac{a}{b}\)
PLEASE HELP!!!OR I WILL GET SIELNT LUNCH.7th GRADE LEVEL HOMEWORK
1 QUESTION.

Answers
You start at (1, 8). You move down 3 units. Where do you end?
Answers
Answer:
(1,5)
Step-by-step explanation:
x = 1
y = 8
If you move down 3 units, it means the y would be lower. This is because y is the vertical value in a pair of coordinates.
8-3 = 5
Answer:
(1, 5)
Step-by-step explanation:
Cartesian Coordinate and TransformationA coordinate defined as point (x, y) is called Cartesian Coordinate. The x-coordinate represents right-left direction while the y-coordinate represents up-down direction.
Its transformation depends on how would you move the coordinate point. An example is if you start with (x, y) point and move to right 3 units, our new position will be at (x + 3, y).
Properties
Suppose we have point (x, y), if we move to right “a” units then the new point will be (x + a, y)
If we move (x, y) to left “a” units, our new point will be (x - a, y)
If we shift (x, y) up “a units”, you’ll get (x, y + a)
If we shift (x, y) down “a units”, we’ll have (x, y - a)
SolutionSuppose you start at (1, 8) and you move down 3 units, you can apply the transformation property to find your new position.
Since you move down, this means you are dealing with y-coordinate only so you’ll apply property of (x, y - a)
You’ll have (1, 8 - 3) which equals to (1, 5).
Hence, you’ll end at (1, 5).
Please let me know if you have any questions!fastt
13. Calculate the compound interest of an annuity due of BD400 paid each 4 months for 6.2 years if the nominal rate is 3% thirdly? (3 Points)
Answers
Therefore, the compound interest of the annuity due of BD 400 paid each 4 months for 6.2 years at a nominal rate of 3% per annum is BD 40,652.17.
Compound interest of an annuity due can be calculated using the formula:A = R * [(1 + i)ⁿ - 1] / i * (1 + i)
whereA = future value of the annuity dueR = regular paymenti = interest raten = number of payments First, we need to calculate the effective rate of interest per period since the nominal rate is given per annum. The effective rate of interest per period is calculated as
:(1 + i/n)^n - 1 = 3/1003/100 = (1 + i/4)^4 - 1
(1 + i/4)^4 = 1.0075i/4 = (1.0075)^(1/4) - 1i = 0.0303So,
the effective rate of interest per 4 months is 3.03%.Next, we can substitute the given values in the formula:
A = BD 400 * [(1 + 0.0303)^(6.2 * 3) - 1] / 0.0303 * (1 + 0.0303)A = BD 400 * [4.227 - 1] / 0.0303 * 1.0303A = BD 400 * 101.63A = BD 40,652.17
For such more question on interest
https://brainly.com/question/25720319
#SPJ8