Find the perimeter and area of a rectangle with width 3 meters and length 11 meters
Answers
Answer:
Perimeter: 28 Meters
Area: 33 Square Meters
Step-by-step explanation:
To calculate the perimeter:
Formula: P = (L + W) × 2
P = (3 + 11) × 2
P = 28 Meters
To calculate the area:
Formula: A = LW
A = 11 × 3
A = 33 Square Meters
Related Questions
HELP NEEDED ASAP
2. Consider the following transformed function
y = −2 Sin [2( − 45°)] + 1
a) Graph the five key points of Parent function on the provided grid. [1mark]
b) State the following for the transformed function [2marks]
Amplitude=
period=
Horizontal Phase shift =
Equation of axis=
c) Graph at least two cycles of the transformed function by transforming the key points of the parent function. (Don’t forget to label the x-axis and y -axis)
Answers
The five key points of the parent function are:
Domain: Set of all real numbersRange: Set of all real numbers from -1 to 1 (inclusive)No vertical asymptoteNo horizontal asymptoteMaximum: (π/2 + 2πn, 1)The five key points of the parent functionThe function is given as:
y = -2 sin[2(x - 45)] + 1
The above function is a sine function, and the parent function of a sine function is
y = sin(x)
The properties of the above function are:
Domain: Set of all real numbersRange: Set of all real numbers from -1 to 1 (inclusive)No vertical asymptoteNo horizontal asymptoteMaximum: (π/2 + 2πn, 1)The transformed functionThe transformed function is given as:
y = -2 sin[2(x - 45)] + 1
A sine function is represented as:
y = A sin[Bx + C] + D
Where:
A represents the amplitudePeriod = 2π/BC represents horizontal phase shiftUsing the above representations, we have:
Amplitude = -2Period = 2π/2 = πHorizontal phase shift, C = 2 * -45 = -90Equation of the axis, y = 1The graph of the functionSee attachment for the graph of the sine function y = -2 sin[2(x - 45)] + 1
Read more about sine functions at:
brainly.com/question/9565966
#SPJ1
![HELP NEEDED ASAP 2. Consider the following transformed functiony = 2 Sin [2( 45)] + 1a) Graph the five](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/eCTld3JxtKBvdEeycvKbaqjBy3BK4B7r.jpeg)
Which of the following are characteristics of a descriptive statistical study? Select all that apply.
Answers
Answer:
you have not given full question.. so please try again.
may this will help you :
Descriptive statistics summarizes or describes the characteristics of a data set. Descriptive statistics consists of two basic categories of measures: measures of central tendency and measures of variability (or spread). Measures of central tendency describe the center of a data set.
URGENT It is given that a regular n-sided polygon has 5 sides more than a
regular m-sided polygon. If the sum of interior angles of the regular
n-sided polygon is twice that of the latter, find the values of m and n.
Answers
Answer:
m = 7; n = 12
Step-by-step explanation:
"a regular n-sided polygon has 5 sides more than a
regular m-sided polygon"
n = m + 5
The sum of the measures of the interior angles is
180(n - 2) for the n-sided polygon and
180(m 2) for the m-sided polygon.
"If the sum of interior angles of the regular
n-sided polygon is twice that of the latter"
180(n - 2) = 2(180)(m - 2)
We have a system of equations with 2 equations.
n = m + 5
180(n - 2) = 2(180)(m - 2)
Simplify the second equation:
n - 2 = 2m - 4
n + 2 = 2m
Substitute m + 5 for n.
m + 5 + 2 = 2m
7 = m
m = 7
n = m + 5 = 7 + 5 = 12
Answer: m = 7; n = 12
Please help me on this question

Answers
Answer:
Angle 4 and angle 5 also equal 180
Because angles 4 and 5 are supplementary angles (two angles that add to 180) and because 4 and 5 equal 180 that means that 5 equals 6. So 5 and 6 are congruence angels
Find the measure of the indicated angle.
N
O
m 20
6yº
3y - 12°
O
M

Answers
Answer:
Here is the answer...hope it helps:)

let a, b,c be three events. write down mathematical expressions (using intersections, unions, complements) of the following events in terms of a, b,c: (i) exactly two of the events hold, (ii) at least one event holds.
Answers
(i) Exactly two of the events hold:
(a ∩ b) ∪ (a ∩ c) ∪ (b ∩ c)
(ii) At least one event holds:
a ∪ b ∪ c
Event Expressions In IntersectionsThe expression for "exactly two of the events hold" is found by considering all possible combinations of two events out of the three events (a, b, c) that can hold, while the other event does not hold. This is achieved by taking the union of the intersections of each combination of two events (a and b, a and c, or b and c) and the complement of the intersection of all three events.
The expression for "at least one event holds" is found by considering the union of all three events, which means that any of the events (a, b, c) can hold independently, or two or all three events can hold simultaneously. This is because the union of events represents the set of outcomes where at least one of the events holds.
Learn more about Event Expressions In Intersections here:
https://brainly.com/question/14333983
#SPJ4
Please explain your answer to this question! Thank you!

Answers
Answer:
B. Incorrectly applied the distributive property
Step-by-step explanation:
You want to find Maria's error in her solution of -2(3x -5) = 40.
StepsThe solution can proceed as follows:
-2(3x -5) = 40 . . . . . . . . given
-6x +10 = 40 . . . . . . . . . use the distributive property
-6x = 30 . . . . . . . . . . subtract 10
x = -5 . . . . . . . . . . divide by -6
Comparing this solution to Maria's, we find that Maria incorrectly applied the distributive property. (She multiplied (-2)(-5) and got -10 instead of +10.)
Carl’s grandfather is exactly 5 times older than Carl.
Which three statements must be true?
please help me
Answers
5*c = g
g/5 = c
g = grandfather
c = carl
Explanation:
The age of Carl's grandfather is a composite number.
Carl's age is a factor of the age of his grandfather.
The number 5 is a factor of the age of Carl's grandfather.
You’re welcome:)
Like it if it makes sense
A marketing firm tracks data on grocery store visits. In one study, it finds that
the probability that a shopper buys bread during a visit to the grocery store is
0.60, and the probability that a shopper buys cheese is 0.20
Event A = A shopper buys bread.
Event B = A shopper buys cheese.
A and B are independent events if
-
A. the probability of buying bread or cheese is 0.12
B. the probability of buying bread and cheese is 0.12
C. the probability of buying bread or cheese is 0.80
D. the probability of buying bread and cheese is 0
Answers
Answer:
B.the probability of buying bread and cheese is 0.12
Step-by-step explanation:
The probability of buying bread and cheese is 0.12.
The correct answer is option B.
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
Example:
The probability of getting a head in tossing a coin.
P(H) = 1/2
We have,
To determine if events A and B are independent,
We need to check if the occurrence of one event affects the probability of the other event.
If the events are independent, the probability of both events occurring can be calculated by multiplying the probabilities of each individual event.
Now,
Let A be the event that a shopper buys bread, and B be the event that a shopper buys cheese.
Then, we know that:
P(A) = 0.60 (the probability of buying bread)
P(B) = 0.20 (the probability of buying cheese)
If A and B are independent events, then the probability of both events occurring (i.e., the shopper buys both bread and cheese) is given by:
P(A and B) = P(A) x P(B)
Substituting the given values.
P(A and B)
= 0.60 x 0.20
= 0.12
This means that the probability of a shopper buying both bread and cheese is 0.12 if events A and B are independent.
Therefore,
The probability of buying bread and cheese is 0.12.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ5
Which equation represents the slope-intercept form of the line below?
y-intercept = (0,-6)
slope = -5
O A. y = -6x + 5
O B. y = -5x - 6
O C. y = -5x + 6
D. y = -6x-5
Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
Option B: \(y=-5x-6\)
»»————- ★ ————-««
Here’s why:
Recall that the slope intercept form of a equation for a line is:⸻⸻⸻⸻
\(\boxed{\text{Slope-Intercept Form:}}\\\\------------\\y=mx+b\\\\\boxed{\text{\underline{Key}}}\\\\\rightarrow\text{m - slope}\\\\\rightarrow\text{b - y-intercept}\)
⸻⸻⸻⸻
We are given the information of:
The slope, which is -5.The y-intercept, which is (0, -6).⸻⸻⸻⸻
\(\boxed{\text{Replace The Variables with The Appropriate Values:}}\\\\y=mx+b\\\\\rightarrow\text{-5 would replace 'm', -6 would replace 'b'.}\\\\\text{\underline{Therefore:}}\\\\y=mx+b\rightarrow\boxed{y=-5x-6}\)
⸻⸻⸻⸻
Option B should be the correct answer.
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
Need Help You Can Get 35 point!!!
The width of a rectangular field is represented by x meters. The length of the field is 10 more than twice its width . The area of the field is 5500m^2
Part A
Write an equation that can be used to determine the dimensions, in meters, of the field.
Part B
What is the width, in meters, of the field?
The width is ( ) meters.

Answers
Part A: The equation that can be used to determine the dimensions, in meters, of the field is 5500 = 2x² + 10x
Part B: width is 50 meters.
How to determine the valueThe formula for calculating the area of a rectangle is expressed with the equation;
A = lw
Such that the variables are expressed as;
A is the areal is the lengthw is the widthWe then have that;
l = 2x + 10
Substitute the values
5500 = (2x + 10)(x)
expand the bracket
5500 = 2x² + 10x
2x² + 10x - 5500
x² + 5x - 2750
x² + 55x - 50x - 2750
x(x + 55) - 50(x + 55)
x = 50 meters
Length = 2(50) + 10
Length = 100 + 10 = 110 meters
Learn about area at: https://brainly.com/question/2607596
#SPJ1
The mean weight of an adult is 6767 kilograms with a variance of 121121. If 164164 adults are randomly selected, what is the probability that the sample mean would be greater than 64.864.8 kilograms
Answers
Answer:
99.48% probability that the sample mean would be greater than 64.8 kilograms.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation(which is the square root of the variance) \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question:
\(\mu = 67, \sigma = \sqrt{121} = 11, n = 164, s = \frac{11}{\sqrt{164}} = 0.86\)
What is the probability that the sample mean would be greater than 64.8 kilograms?
This is 1 subtracted by the pvalue of Z when X = 64.8.
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{64.8 - 67}{0.86}\)
\(Z = -2.56\)
\(Z = -2.56\) has a pvalue of 0.0052
1 - 0.0052 = 0.9948
99.48% probability that the sample mean would be greater than 64.8 kilograms.
It is assumed that the test results for a class follow a normal distribution with a mean of 78 and a standard deviation of 36. If you know that a student's grade is greater than 72, what is the probability that it is greater than 84
Answers
Answer: 0.4337
Step-by-step explanation:
Let X represents the test results for a class that follow a normal distribution .
Given: Mean \(\mu=78\), Standard deviation \(\sigma=36\)
Then, the probability that it is greater than 84 will be
\(P(X>84)=P(\dfrac{X-\mu}{\sigma}>\dfrac{84-78}{36})\\\\=P(Z>0.167)\ \ \ [Z=\dfrac{X-\mu}{\sigma}]\\\\=1-P(Z<0.167)\\\\=1-0.5663=0.4337\ [\text{By p-value table}]\)
Hence, the required probability = 0.4337
The center of the circle whose equation is (x + 2)² + (y - 3)² = 25 is
Answers
Answer:
The center of the circle is at: C=(−2,3).
The radius of the circle is r=5.
Step-by-step explanation:
A circle with center at (h,k) and a radius of r has equation (x−h)2+(y−k)2=r2.
In this example our circle equation can be written as:
(x−(−2))2+(y−3)2=(5)2
So, we have: h=−2 , k=3 and r=5.
Gabriel's boss tells him he must
pack 12 boxes every quarter-hour.
How many boxes must Gabriel
pack in one hour?
Answers
Answer:
48
Step-by-step explanation:
simple,
a quarter is split into 4
so u do 12x4
A recent survey showed that exactly 38%
of people in a town buy the local
newspaper. There are 2450 people in the
town.
a) How many people in the town buy the
local newspaper?
b) How many people in the town do not
buy the local newspaper?
Answers
Answer:
a) .38 × 2,450 = 931 people buy the local newspaper.
b) 2,450 - 931 = 1,519 people do not buy the local newspaper.
Which statement defines Suppose that farmers grew an unexpectedly large number of tomatoes this year. How would this increase in production affect the price of tomatoes?the term markup?
Answers
Answer:
The price would go down as people would be more willing to buy cheaper potatoes and the producers would want to sell them for a lower price to get rid of them easy and fast.
Step-by-step explanation:
Hope this helps you :)
integration of sin3xsinx
Answers
Recall that
cos(x + y) = cos(x) cos(y) - sin(x) sin(y)
cos(x - y) = cos(x) cos(y) + sin(x) sin(y)
If you subtract the first equation from the second one, you end up with
cos(x - y) - cos(x + y) = 2 sin(x) sin(y)
so that
sin(3x) sin(x) = 1/2 (cos(3x - x) - cos(3x + x)) = 1/2 (cos(2x) - cos(4x))
Then in the integral,
\(\displaystyle \int \sin(3x)\sin(x)\,\mathrm dx = \frac12 \int(\cos(2x)-\cos(4x))\,\mathrm dx \\\\ = \frac12 \left(\frac12 \sin(2x) - \frac14 \sin(4x)\right) + C \\\\ = \boxed{\frac14 \sin(2x) - \frac18 \sin(4x) + C}\)
How much commission will George receive for the sale of a $250,000 home if he receives 2 1/2% of the selling price?
Answers
Answer:
625,000
Step-by-step explanation:
250,000 * 5/2 = 625,000
The commission that George will receive for the sale of a \(\$\)250,000, if he receives 2 1/2% of the selling price is $6,250.
What is commission?"A commission is a piece of work that someone is asked to do and is paid for."
Sale is \(\$\)250,000
Converting 2 1/2% in improper fraction is 5/2 %
So, commission will be \(\(2.5*250,000 /100\) = 625,000/100 = 6250
Hence, the commission that George will receive is $6,250.
To know more about commission here
https://brainly.com/question/20520174
#SPJ2
URGENT NEED HELP RIGHT ANSWER WILL BE BRAINLEIST
Write an absolute value equation with the SOLUTION OF -1 and 5.
Answers
Answer:
i had given detailed solution mark me brainliest.
thank you


A company created a new container in the shape of a
triangular prism that will hold sunflower seeds. A three-
dimensional image of the container is shown below, as
well as a two-dimensional image of the base.
6 in.
3.2 in.
2 in.
3.2 in.
1 in.
square inches
1 in.
The container will be made from cardboard. How many
square inches of cardboard are needed to make one
container? Assume there are no overlapping areas.

Answers
The number of square inches of cardboard that are needed to make one
the container is 18.
We have,
The volume of the triangular prism.
= Area of the triangle x height
Now,
Height = 6 in
And,
To find the area of a triangle, we can use Heron's formula.
A = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case, the side lengths of the triangle are 3.2 in, 3.2 in, and 2 in.
Let's calculate the area using Heron's formula:
s = (3.2 + 3.2 + 2) / 2 = 4.2
A = √(4.2(4.2 - 3.2)(4.2 - 3.2)(4.2 - 2))
A = √(4.2 x 1 x 1 x 2.2)
A = √(9.24)
A ≈ 3.04 square inches
Now,
The volume of the triangular prism.
= Area of the triangle x height
= 3.04 x 6
= 18.24 in²
Now,
Area of one cardboard.
= 1² in²
= 1 in²
Now,
The number of square inches of cardboard that are needed to make one
container.
= The volume of the triangular prism / Area of one cardboard
= 18.24 in² / 1 in²
= 18.24
= 18
Therefore,
The number of square inches of cardboard that are needed to make one
the container is 18.
Learn more about Prism here:
https://brainly.com/question/12649592
#SPJ1
Find the volume of the cone
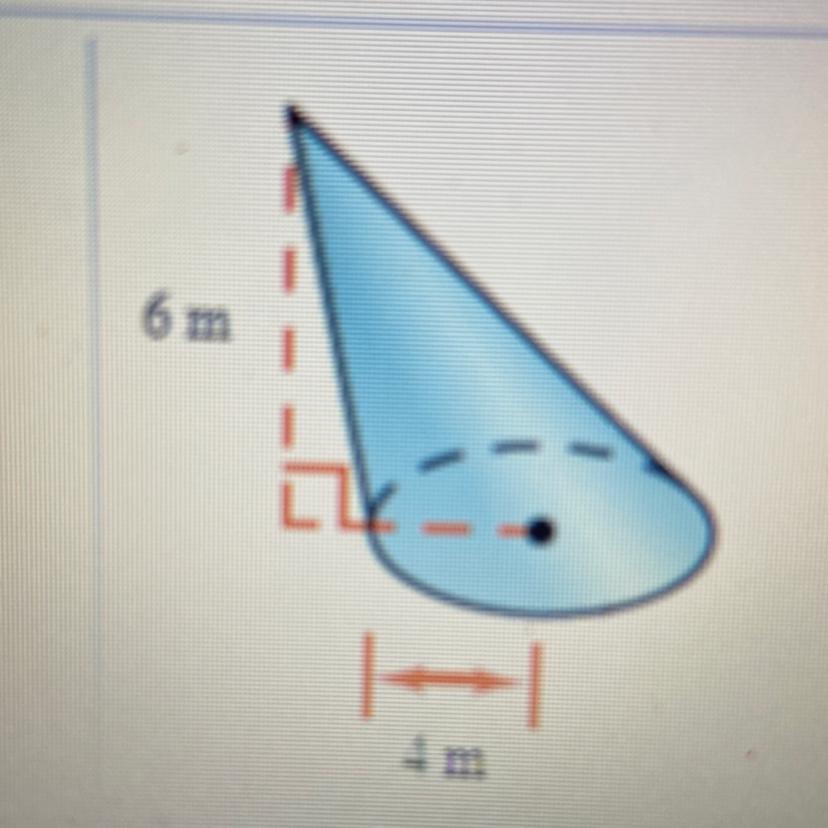
Answers
Answer:
100.53
Step-by-step explanation:
V = π r^2 h/3fill in what you know V= π 4^2 6/3solveThe center of a circle is at the origin on a coordinate grid. The vertex of a parabola that opens upward is at (0, 9). If the
circle intersects the parabola at the parabola's vertex, which statement must be true?
O The maximum number of solutions is one.
O The maximum number of solutions is three.
O The circle has a radius equal to 3.
The circle has a radius less than 9.
Answers
As a result, there must be an x value such that the inequality is no longer true, and the parabola and the circle must intersect as a result.
The circle is centered at the origin on a coordinate grid, and the vertex of an upward-opening parabola is located at (0, 9). If the circle has a radius less than 9, the parabola and the circle must intersect.Let's suppose that the upward-opening parabola is y = ax² + 9. Since its vertex is (0, 9), this implies that a > 0, and therefore the parabola opens upwards. Since the circle is centered at the origin and has a radius less than 9, its equation is x² + y² < 81.We can substitute y with ax² + 9 in the inequality x² + y² < 81 and obtain:x² + (ax² + 9)² < 81This simplifies to:(a² + 1) x^4 + 18a² x² + 64 < 0Since the left-hand side of the inequality must be less than zero, it must be negative. Since x² is always non-negative, it follows that a² + 1 > 0. Thus, (a² + 1) x^4 + 18a² x² + 64 < 0 cannot be true for all x
for more search question inequality
https://brainly.com/question/25275758
#SPJ8
An entrepreneur invests in a new play. The cost includes an overhead of $33,750 plus production costs of $1700 per performance. A sold-out performance brings in $2325 . Assume every performance is sold out, and let x represent the number of sold-out performances.
Answers
The entrepreneur's revenue is $2325x, entrepreneur's cost is $33,750 + $1700x and entrepreneur's profit from x sold-out performances is $625x - $33,750
The entrepreneur's revenue from x sold-out performances is given by the formula:
Revenue = (Price per Performance) x (Number of Performances)
Revenue = $2325 x x
Revenue = $2325x
The entrepreneur's cost from x sold-out performances is given by the formula:
Cost = Overhead + (Production Cost per Performance) x (Number of Performances)
Cost = $33,750 + $1700x
The entrepreneur's profit from x sold-out performances is the revenue minus the cost:
Profit = Revenue - Cost
Profit = $2325x - ($33,750 + $1700x)
Profit = $625x - $33,750
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
In a sale, all normal prices are reduced by 15%
The normal price of a mixer is reduced by 22.50 dollars.
Work out the normal price of the mixer.
Answers
Answer:
The normal price of mixer is $150.
Step-by-step explanation:
Given that:
Normal prices are reduced by 15% in sale.
The normal price of mixer is reduced by $22.50
It means that it is the amount of discount.
Let,
x be the normal price of the mixer.
15% of x = 22.50
\(\frac{15}{100}x=22.50\\0.15x=22.50\)
Dividing both sides by 0.15
\(\frac{0.15x}{0.15}=\frac{22.50}{0.15}\\x=150\)
Hence,
The normal price of mixer is $150.
The normal price of the mixer is $150.
Given that,
In a sale, all normal prices are reduced by 15% The normal price of a mixer is reduced by 22.50 dollars.Based on the above information, the calculation is as follows;
Let us assume the normal price be x
15%x = 22.50
0.15x = 22.50
x = $150
Learn more: brainly.com/question/16911495
ITS A SIMPLE 50 POINT QUESTION! PLEASE HELP!
is y = 4 a relation?
Answers
Answer:
Y=4 is a function
Step-by-step explanation:
And to me function is relation
Hope i got this right and have a great day :)
Answer: Yes
Step-by-step explanation:
Yes, y = 4, which is often written as f(x) = 4, is a function that means “take any input, and no matter what it is, produce an output of 4”.
HELP PLEASE I WILL MARK BRAINIEST WHEN ABLE TO
An expression is shown below:
the square root of 18 plus the square root of 2
Which statement is true about the expression?
It is rational and equal to 4 times the square root of 2.
It is irrational and equal to 4 times the square root of 2.
It is rational and equal to 3 times the square root of 2.
It is irrational and equal to 3 times the square root of 2.
Answers
Answer: It is irrational and equal to 3 times the square root of 2.
Answer:
It is irrational and equal to 3 times the square root of 2.
Step-by-step explanation:
just like the other guy said
A baseball team plays in a stadium that holds 74000 spectators. With the ticket price at $9 the average attendance has been 30000. When the price dropped to $8, the average attendance rose to 37000. Assume that attendance is linearly related to ticket price. What ticket price would maximize revenue
Answers
Answer:
solution
$9=30000
$8=37000
$?=74000
=$3
write the slope-intercept form of the equation of each line

Answers
Answer:
y = 2x - 5
Step-by-step explanation:
Slope = 2
y-intercept = - 5
In kite WXYZ, m∠X=90° and m∠Z=40°. Therefore, m∠W is
Answers
The measure of angle W in the kite WXYZ is 115°
What are kites?A kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides.
Given that, In kite WXYZ, m ∠ x = 90° and m ∠ z =40°.
Please refer to figure attached,
We know that, in a kite, it has two opposite and equal angles.
According to figure, here,
m ∠ W = m ∠ Y
Let m ∠ W = m ∠ Y = x
Also, the sum of interior angles of quadrilateral = 360°
Therefore,
x + x + 90° + 40° = 360°
2x = 360° - 130°
2x = 230°
x = 115°
Thus, m ∠ W = m ∠ Y = 115°
Hence, the measure of angle W in the kite WXYZ is 115°
Learn more about kite, click;
https://brainly.com/question/19246521
#SPJ1