Find the slope of the line with points: (-5,3) and (3, -5).
Answers
Answer:
slope = - 1
Step-by-step explanation:
calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 5, 3 ) and (x₂, y₂ ) = (3, - 5 )
m = \(\frac{-5-3}{3-(-5)}\) = \(\frac{-8}{3+5}\) = \(\frac{-8}{8}\) = - 1
Related Questions
are all isosceles triangles similar
Answers
Answer:
Step-by-step explanation:
isosceles triangles are all similar in that they have 2 sides that are equal.
however, the angles can differ and so they are not all similar in that term
Let X and Y be continuous random variables with joint density function fxy(x,y)= [c(x+y) 0
Answers
The value of c is 36/5. Thus, the joint density function of X and Y is fxy(x, y) = [36/5(x + y)] 0 < x < 2, 0 < y < 1.
X and Y are continuous random variables with joint density function
fxy(x, y) = [c(x + y) 0 < x < 2, 0 < y < 1],
where c is a constant to be determined. The constant c can be calculated by using the property that the integral of the joint density function over the entire plane must equal 1. i.e.,
∫∫fxy(x, y) dydx = 1,
where the limits of integration are 0 to 1 for y and 0 to 2 for x.
Here, the joint density function fxy(x, y) is defined as
fxy(x, y) = c(x + y) 0 < x < 2, 0 < y < 1.
The integral of the joint density function over the entire plane is
∫∫fxy(x, y) dydx = c∫∫(x+y) dydx
=c∫[0,2]∫[0,1](x+y)dydx
= c ∫[0,2](xy+ y²/2)dx
= c [(x²y/2) + xy²/2] 0 ≤ y ≤ 1; 0 ≤ x ≤ 2
= c [(2y/2) + y²/2] 0 ≤ y ≤ 1
= c [(y + y²/2)]dy
= c [(y²/2 + y³/6)] 0 ≤ y ≤ 1
= c [1/12 + 1/18]
= c [(3 + 2)/36]
= 5c/36
The integral of the joint density function over the entire plane is equal to 1. Therefore, we have 5c/36 = 1
c = 36/5
The question is incomplete, the complete question is "Let X and Y be continuous random variables with joint density function fxy(x,y)= [c(x+y) 0. Calculate the value of c."
You can learn more about density function at: brainly.com/question/31039386
#SPJ11
given ∫16f(x)dx=13and∫65f(x)dx=−2, compute the following integral. ∫512f(x)dx
Answers
The value of the integral ∫₅¹² f(x)dx is 15.
To compute the integral ∫₅¹² f(x)dx, we can use the properties of definite integrals, specifically the linearity property and the change of limits.
Since the integral is from 5 to 12, and we are given information about the integral from 1 to 6 and from 6 to 5, we can break down the integral into two parts and combine them using the properties of integrals.
First, we can rewrite the given integral ∫₅¹² f(x)dx as the sum of two integrals:
∫₅¹² f(x)dx = ∫₅⁶ f(x)dx + ∫₆¹² f(x)dx
Now, we can use the given information:
∫₁⁶ f(x)dx = 13
∫₆⁵ f(x)dx = -2
Applying the change of limits to the second integral:
∫₆¹² f(x)dx = -∫₁₂⁶ f(x)dx
We can now express the integral ∫₅¹² f(x)dx as:
∫₅¹² f(x)dx = ∫₅⁶ f(x)dx + ∫₆¹² f(x)dx
= ∫₅⁶ f(x)dx - ∫₁₂⁶ f(x)dx
Since the limits of integration in the second integral are reversed, we can change the sign of the integral and adjust the limits:
∫₅¹² f(x)dx = ∫₅⁶ f(x)dx - ∫₆¹² f(x)dx
= ∫₁⁶ f(x)dx - ∫₆⁵ f(x)dx
= 13 - (-2)
= 13 + 2
= 15
Therefore, the value of the integral ∫₅¹² f(x)dx is 15.
Learn more about Integration here
https://brainly.com/question/29754607
#SPJ4
PLEASE HELP IF U GET IT RIGHT I WILL MARK BRAINLIEST PLEASE ITS DUE IN 9 MINS

Answers
Answer: y = 1x+ -2 or y=x-2
Step-by-step explanation:
y=mx+b
-10=1(-8)+b
-10=-8+b
b=-2
Answer:
y=x-2
Step-by-step explanation:
y-(-10)=1(x-(-8)
y+10=1(x+8)
y+10=1x+8
y=1x+8-10
y=1x-2
A triangle has sides length of (4.1p+4.4q) centimeter,(6.4p-5.1r)centimeters ,and (1.3r+6.3q)centimeters . Which expression represents the perimeter , in centimeter , of triangle ?
Answers
Answer:
The perimeter of the rectangle is 10.5p + 10.7q - 3.8r
Step-by-step explanation:
The perimeter of the triangle is calculated by adding the values of the three sides.
In this case, the values of the individual sides are expressed algebraically.
We can still add them, however, taking into consideration like terms.
Perimenter of triangle = (4.1p+4.4q) + (6.4p-5.1r) + (1.3r+6.3q)
Perimeter = 4.1p + 6.4p + 4.4q + 6.3q -5.1r + 1.3r
Now we have grouped them, we can add the different groups separately
Perimeter = 10.5p + 10.7q - 3.8r
Therefore, the perimeter of the rectangle is 10.5p + 10.7q - 3.8r
Find the divergence of the vector field. F(x, y, z) = 5x²7 - sin(xz) (i+k)
Answers
The divergence of the vector field F(x, y, z) = (5x^2 + 7 - sin(xz))i + 0j + (5x^2 + 7 - sin(xz))k is 20x - 2zcos(xz).
To find the divergence of the vector field F(x, y, z) = (5x^2 + 7 - sin(xz))i + 0j + (5x^2 + 7 - sin(xz))k, you need to take the divergence operator (∇ · F).
The divergence of a vector field in Cartesian coordinates is given by the following formula:
∇ · F = (∂Fx/∂x) + (∂Fy/∂y) + (∂Fz/∂z),
where Fx, Fy, and Fz are the x, y, and z components of the vector field F, respectively.
In this case, we have:
Fx = (5x^2 + 7 - sin(xz)),
Fy = 0, and
Fz = (5x^2 + 7 - sin(xz)).
Taking the partial derivatives, we get:
∂Fx/∂x = 10x - zcos(xz),
∂Fy/∂y = 0, and
∂Fz/∂z = 10x - zcos(xz).
Now, substituting these derivatives into the divergence formula, we have:
∇ · F = (10x - zcos(xz)) + 0 + (10x - zcos(xz)).
Simplifying further, we get:
∇ · F = 20x - 2zcos(xz).
Therefore, the divergence of the vector field F(x, y, z) = (5x^2 + 7 - sin(xz))i + 0j + (5x^2 + 7 - sin(xz))k is 20x - 2zcos(xz).
Learn more about divergence at https://brainly.com/question/32669520
#SPJ11
Need help asap. What is the volume of the given prism? the figure is not drawn to scale.

Answers
1.
(04.02 LC)
Which of the following is a common characteristic of a binomial distribution? (4 points)
There are more than two possible outcomes.
The probability of success is the same in all trials.
There are infinitely many observations.
You should perform x trials until you observe a success.
Each trial is dependent on the previous trial.
Answer: The probability of success is the same in all trials.
Answers
The probability of success, p, is the same for each trial. Each outcome is either a success (P) or a failure (Q). The correct option is A.
What is the independent probability?Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes.
You should perform x trials until you observe a success.
We have given that,
There are exactly two possible outcomes success and failure.
We have to determine the following is NOT a common characteristic of a binomial distribution.
By process of elimination:-
A binomial experiment is a statistical experiment that must meet certain requirements
All trials are independent.
There are a fixed number of n trials.
The probability of success, p, is the same for each trial.
To learn more about the probability visit:
brainly.com/question/24756209
#SPJ1
PLEASE HELP AND MAKE SURE ITS CORRECT IF ITS CORRECT I WILL GIVE BRAINLIST :)
What is the circumference of the circle with a radius of 5.5 meters? Approximate using π = 3.14.
6.45 meters
34.54 meters
38.47 meters
199.66 meters
Answers
Answer:
34.54
Step-by-step explanation:
To find the circumference of a circle, you need the formula 2π r^2. The radius is 5.5 so substitute that in for r (radius).
can someone
please help and fast

Answers
Answer:18
Step-by-step explanation:
same as other side 90 degrees
Please help!
Describe the characteristics of the function shown.
Look at image to understand.

Answers
Answer:
-∞0negativeStep-by-step explanation:
You want the end behavior and the sign of the function y = -3/5(5/7)^x.
End behaviorThis is an exponential function, so it will tend toward 0 in one direction and toward infinity in the other direction. The sign of the infinity will match the sign of the multiplier. The base of the exponent here is less than 1, so the tendency toward 0 will occur for positive values of x.
y → -∞ as x → -∞
y → 0 as x → +∞
y < 0 for all x . . . (y is negative)

in general, assuming > 0, what is the probability that the decoder will know with certainty what the source bit was?
Answers
The characteristics of the channel or transmission medium, and other factors related to the specific system being considered.
What is the probability that the decoder will know with certainty what the source bit was?If we assume that the probability of error (the probability that the decoder will make a mistake) is greater than 0, then the probability that the decoder will know with certainty what the source bit was is 1 minus the probability of error.
Let's denote the probability of error as p_error. The probability that the decoder will know the source bit with certainty (probability of correct decoding) can be expressed as:
P_correct = 1 - p_error
Since we assume that p_error is greater than 0, the probability of correct decoding will be less than 1 but greater than 0.
It's important to note that this is a general concept and the specific value of p_error would depend on the decoding algorithm, the characteristics of the channel or transmission medium, and other factors related to the specific system being considered.
Learn more about probability
brainly.com/question/32117953
#SPJ11
Continue the sequence by increasing each number in powers of 1000:
11345,____,____,____,____,____.
Answers
Answer:
12345,13345,14345,15345,16345
Step-by-step explanation:
A landscaping company has collected data on home values (in thousands of $) and expenditures (in thousands of $) on landscaping with the hope of developing a predictive model to help marketing to potential new clients. Suppose the following table represents data for 14 households.
Home
Value
($1,000) Landscaping
Expenditures
($1,000)
241 8.2
322 10.7
199 12.3
340 16.1
300 15.7
400 18.8
800 23.5
200 9.5
522 17.5
546 22.0
438 12.2
463 13.5
635 17.8
357 13.8
(a)
Develop a scatter diagram with home value as the independent variable.
A scatter diagram has a horizontal axis labeled "Home Value ($1,000)" with values from 0 to 900 and a vertical axis labeled "Landscaping Expenditures ($1,000)" with values from 0 to 25. The scatter diagram has 14 points. A pattern goes down and right from (199, 21.8) to (800, 6.5). The points are scattered moderately from the pattern.
A scatter diagram has a horizontal axis labeled "Home Value ($1,000)" with values from 0 to 900 and a vertical axis labeled "Landscaping Expenditures ($1,000)" with values from 0 to 25. The scatter diagram has 14 points. A pattern goes up and right from (199, 8.2) to (800, 23.5). The points are scattered moderately from the pattern.
A scatter diagram has a horizontal axis labeled "Landscaping Expenditures ($1,000)" with values from 0 to 25 and a vertical axis labeled "Home Value ($1,000)" with values from 0 to 900. The scatter diagram has 14 points. A pattern goes down and right from (6.5, 800) to (21.8, 199). The points are scattered moderately from the pattern.
A scatter diagram has a horizontal axis labeled "Landscaping Expenditures ($1,000)" with values from 0 to 25 and a vertical axis labeled "Home Value ($1,000)" with values from 0 to 900. The scatter diagram has 14 points. A pattern goes up and right from (8.2, 199) to (23.5, 800). The points are scattered moderately from the pattern.
(b)
What does the scatter plot developed in part (a) indicate about the relationship between the two variables?
The scatter diagram indicates no apparent relationship between home value and landscaping expenditures.The scatter diagram indicates a nonlinear relationship between home value and landscaping expenditures. The scatter diagram indicates a negative linear relationship between home value and landscaping expenditures.The scatter diagram indicates a positive linear relationship between home value and landscaping expenditures.
(c)
Use the least squares method to develop the estimated regression equation. (Let x = home value (in thousands of $), and let y = landscaping expenditures (in thousands of $). Round your numerical values to five decimal places.)
ŷ =
(d)
For every additional $1,000 in home value, estimate how much additional will be spent (in $) on landscaping. (Round your answer to the nearest cent.)
$
(e)
Use the equation estimated in part (c) to predict the landscaping expenditures (in $) for a home valued at $475,000. (Round your answer to the nearest dollar.)
$
Answers
(a) A scatter diagram has a horizontal axis labeled "Home Value ($1,000)" with values from 0 to 900 and a vertical axis labeled "Landscaping Expenditures ($1,000)" with values from 0 to 25.
The scatter diagram has 14 points.
A pattern goes up and right from (199, 8.2) to (800, 23.5). The points are scattered moderately from the pattern.
(b) The scatter plot developed in part (a) indicates a positive linear relationship between home value and landscaping expenditures.
(c) Using the least squares method, the estimated regression equation is: ŷ = 0.02794x + 0.74872
(d) For every additional $1,000 in home value, an estimated additional $27.94 will be spent on landscaping.
(e) Using the estimated regression equation from part (c), the predicted landscaping expenditures for a home valued at $475,000 would be $13,027.
We have,
(a) The scatter diagram is a visual representation of the data points plotted on a graph, where the horizontal axis represents the home value and the vertical axis represents the landscaping expenditures.
The correct answer describes the correct labeling of the axes and the position of the points in relation to the pattern.
(b) The scatter plot shows the overall relationship between home value and landscaping expenditures.
In this case, the correct answer states that there is a positive linear relationship, meaning that as the home value increases, the landscaping expenditures also tend to increase.
This can be observed from the pattern in the scatter diagram.
(c) The least squares method is a statistical technique used to find the best-fitting line through the data points.
By applying this method, we can determine the estimated regression equation that represents the relationship between home value and landscaping expenditures.
The correct answer provides the specific equation:
ŷ = 0.02794x + 0.74872, where ŷ represents the estimated landscaping expenditures and x represents the home value.
(d) The estimated regression equation from part (c) allows us to estimate the additional amount spent on landscaping for every additional $1,000 in home value.
The correct answer states that for every additional $1,000 in home value, an estimated additional $27.94 will be spent on landscaping.
(e) Using the estimated regression equation from part (c), we can make predictions for specific scenarios.
In this case, the correct answer asks for the predicted landscaping expenditures for a home valued at $475,000.
By substituting the given home value into the regression equation, we can estimate the corresponding landscaping expenditures.
The correct answer states that the predicted landscaping expenditures for a home valued at $475,000 would be $13,027.
This prediction is based on the relationship observed in the data.
Thus,
(a) A scatter diagram has a horizontal axis labeled "Home Value ($1,000)" with values from 0 to 900 and a vertical axis labeled "Landscaping Expenditures ($1,000)" with values from 0 to 25.
The scatter diagram has 14 points.
A pattern goes up and right from (199, 8.2) to (800, 23.5). The points are scattered moderately from the pattern.
(b) The scatter plot developed in part (a) indicates a positive linear relationship between home value and landscaping expenditures.
(c) Using the least squares method, the estimated regression equation is: ŷ = 0.02794x + 0.74872
(d) For every additional $1,000 in home value, an estimated additional $27.94 will be spent on landscaping.
(e) Using the estimated regression equation from part (c), the predicted landscaping expenditures for a home valued at $475,000 would be $13,027.
Learn more about regression lines here:
https://brainly.com/question/30243761
#SPJ4
i don’t understand plz help

Answers
Answer:
The converse of P ⇒ Q is Q ⇒ P.
The inverse of P ⇒ Q is (¬ P) ⇒ (¬ Q).
The contrapositive of P ⇒ Q is (¬ Q) ⇒ (¬ P).
Given two statements P and Q, the biconditional statement P ⇔ Q is the statement “P if and only if Q.” The biconditional statement P ⇔ Q is true when P and Q have the same truth values and false when P and Q have different truth values.
Find the greatest common factor of 20, 70, and 50.
Answers
Answer:
=10
Step-by-step explanation:
because 20÷10=2
70÷10=7
50÷10=5
Please help me I am in a hurry to go somewhere so please help quick
Three sisters are each less than 45 years old. The mode of their ages is 35. The range is 14. What is the mean of their ages? The median?
a.
29.7; 35
c.
35; 30.3
b.
30.3; 28
d.
30.3; 35
Please select the best answer from the choices provided
sorry about the answer choices being mixed up im still in a hurry
Answers
Answer:
I'm so sorry I don't know this answer but good luck
Answer: since it doesn't tell you how you get it.
Since the mode of the ages is 35 we know that at least two of the ages are 35. Since the range is 14 we know the third sister is not also age 35. Let x be the age of the third sister. Then we know either 35 - x = 14 or x-35 = 14 (depending if x is younger or older, respectively). Solving both of these gives x = 21 or x = 49. But all the sisters are under the age of 45, so x = 21. Hence, the ages of the sisters are
21, 35, 35.
So, the mean is (35+35+21)/3 = 91/3 =~ 30.3333 ...
The median is 35.
What is the volume of the cylinder below? Write your answer in terms of π

Answers
Answer:
The answer would be 414 . good luck ^^
If A is symmetric matrix, then A^3 is a _______ matrix.
Answers
If A is a symmetric matrix, then A³ is also a symmetric matrix.
To prove this, we can use the definition of a symmetric matrix, which is a matrix that is equal to its transpose. In other words, if A is a symmetric matrix, then A = A^T.
Now, let's look at A³:
A³ = A * A * A
We can replace each A with A^T, since they are equal:
A³ = A^T * A^T * A^T
Now, we can use the property that the transpose of a product of matrices is equal to the product of their transposes in reverse order:
A³ = (A^T * A^T * A^T)^T
A³ = (A^T)^T * (A^T)^T * (A^T)^T
Since the transpose of a transpose is the original matrix, we can simplify:
A³ = A * A * A
Therefore, A³ is also a symmetric matrix.
More information about the symmetric matrix here:
https://brainly.com/question/16374195
#SPJ11
Data (S) 0 1 2 2.3 2.7 2.8 3 4 5 6 7 8 9 10 11 12 13 13.1 14 15
a(m/s²) 0 0 0 0 6.5 -9.8 ----------------------------> -9.8 0 0 0
(m = 250 g)
Questions :
1. Usethe appropriate relationship to arrive at the Rf value for the data provided
W calculation --> 2 marks
Sample Rf calculation (for a non zero "a")--> 2 marks
All Rf values filled in --> 1 mark
2. Plot a force vs time history of this event --> 3 marks
3. desribe the events taking place during the following time frames --> 2 marks
a) 0 to 2.3 s
b) 2.3 to 2.7 s
c) 2.8 to 13 s
d) 13.1 to 15 s
Answers
The provided data consists of a set of values for time (s) and acceleration (m/s²). To calculate the Rf values, we need to determine the change in velocity (Δv) during each time interval and divide it by the corresponding time interval (Δt).
The Rf value represents the rate of change of velocity. The force vs. time graph can be plotted using the provided data points. By analyzing the time frames, we can describe the events occurring during each interval.
1. To calculate the Rf values, we need to determine the change in velocity (Δv) during each time interval and divide it by the corresponding time interval (Δt). Since the provided data includes acceleration values (a), we can use the equation v = u + at, where v is the final velocity, u is the initial velocity (assumed to be zero in this case), a is the acceleration, and t is the time. By calculating the changes in velocity and dividing them by the respective time intervals, we can obtain the Rf values for each interval. However, since the acceleration is not provided for all intervals, it is not possible to calculate the Rf values for those intervals.
2. Plotting a force vs. time graph requires knowing the mass (m) of the object. In this case, the mass is given as 250 g (0.25 kg). To calculate the force (F), we can use Newton's second law of motion, F = ma, where m is the mass and a is the acceleration. By multiplying the mass with the corresponding acceleration values for each time interval, we can obtain the force values. Plotting these force values against the corresponding time intervals will give us the force vs. time history of the event.
3. Analysis of the time frames:
a) During the time interval from 0 to 2.3 seconds, the object experiences zero acceleration, indicating that it is at rest.
b) From 2.3 to 2.7 seconds, the object experiences an acceleration of 6.5 m/s², suggesting that it is undergoing positive acceleration.
c) Between 2.8 and 13 seconds, the object experiences a constant negative acceleration of -9.8 m/s². This indicates that the object is slowing down.
d) From 13.1 to 15 seconds, the object once again experiences zero acceleration, implying that it comes to a stop.
In summary, the provided data allows us to calculate the Rf values for the intervals where acceleration is given. Additionally, we can plot a force vs. time graph using the provided mass and acceleration data. By analyzing the time frames, we can infer that the object remains at rest initially, undergoes positive acceleration, then experiences a constant negative acceleration until it comes to a stop at the end of the given time interval.
To learn more about Rf click here: brainly.com/question/32150693
#SPJ11
Suppose we have a test for a disease. Assume that
(1) the sensitivity of the test is 99%, that is, the probability that the test is positive for a person with the disease is 0.99;
(2) the specificity of the test is 98%, that is, the probability that the test is negative for a person without the disease is 0.98;
(3) the prevalence of the disease is one in two hundred, that is, the probability of a random person carrying the disease is 0.005.
The probability that someone with a positive test actually has the disease is called the positive predictive value of the test. Express the positive and negative predictive value of the test using conditional probabilities and compute them using Bayes formula.
Answers
The positive predictive value (PPV) and negative predictive value (NPV) of a test can be calculated using conditional probabilities and Bayes' formula. In this scenario, the sensitivity of the test is 99%, specificity is 98%, and the prevalence of the disease is 0.005. PPV represents the probability that a person with a positive test result actually has the disease, while NPV represents the probability that a person with a negative test result does not have the disease.
To calculate the positive predictive value (PPV), we need to find the probability that someone with a positive test actually has the disease. We can use Bayes' formula, which states that:
PPV = (Sensitivity * Prevalence) / [(Sensitivity * Prevalence) + [(1 - Specificity) * (1 - Prevalence)]]
Plugging in the given values, we have:
PPV = (0.99 * 0.005) / [(0.99 * 0.005) + [(1 - 0.98) * (1 - 0.005)]]
Simplifying the equation gives us:
PPV ≈ 0.3328 or 33.28%
Therefore, the positive predictive value of the test is approximately 33.28%.
Similarly, to calculate the negative predictive value (NPV), we need to find the probability that a person with a negative test result does not have the disease. The formula for NPV is:
NPV = (Specificity * (1 - Prevalence)) / [(Specificity * (1 - Prevalence)) + [(1 - Sensitivity) * Prevalence]]
Using the given values, we can calculate:
NPV = (0.98 * (1 - 0.005)) / [(0.98 * (1 - 0.005)) + [(1 - 0.99) * 0.005]]
Simplifying the equation gives us:
NPV ≈ 0.9999 or 99.99%
Therefore, the negative predictive value of the test is approximately 99.99%.
In summary, the positive predictive value (PPV) of the test is approximately 33.28%, indicating the probability that someone with a positive test actually has the disease. The negative predictive value (NPV) is approximately 99.99%, representing the probability that someone with a negative test result does not have the disease.
Learn more about probability here: https://brainly.com/question/31828911
#SPJ11
y=f(x)=-3^x find f(x) when x=1
Answers
Answer:
\(f(x) = { - 3}^{x} \\ f(1) = - {3}^{1} = - 3\)
Help me with question 21 to get brainliest

Answers
Step-by-step explanation:
We can call the original value x. In 2012, the painting's value was 1.05 x. In the beginning of 2013, the value was (1.05 x) * 0.98, and that increased to (1.05x) * 0.98 * 1.40 at the end of 2013. When we simplify, we get 1.4406 x as a value, and we know that this is equal to $52,640. We can write 1.4406x = 52640, and when we solve for x, we get x ≈ $36415.38. Hope this helps!
What is the range of the following data set? {4, 7. 3. 9. 7. 8. 6. 7. 4. 3}
Answers
Answer:
range = 6
Step-by-step explanation:
Highest number - lowest number
9 - 3
= 6
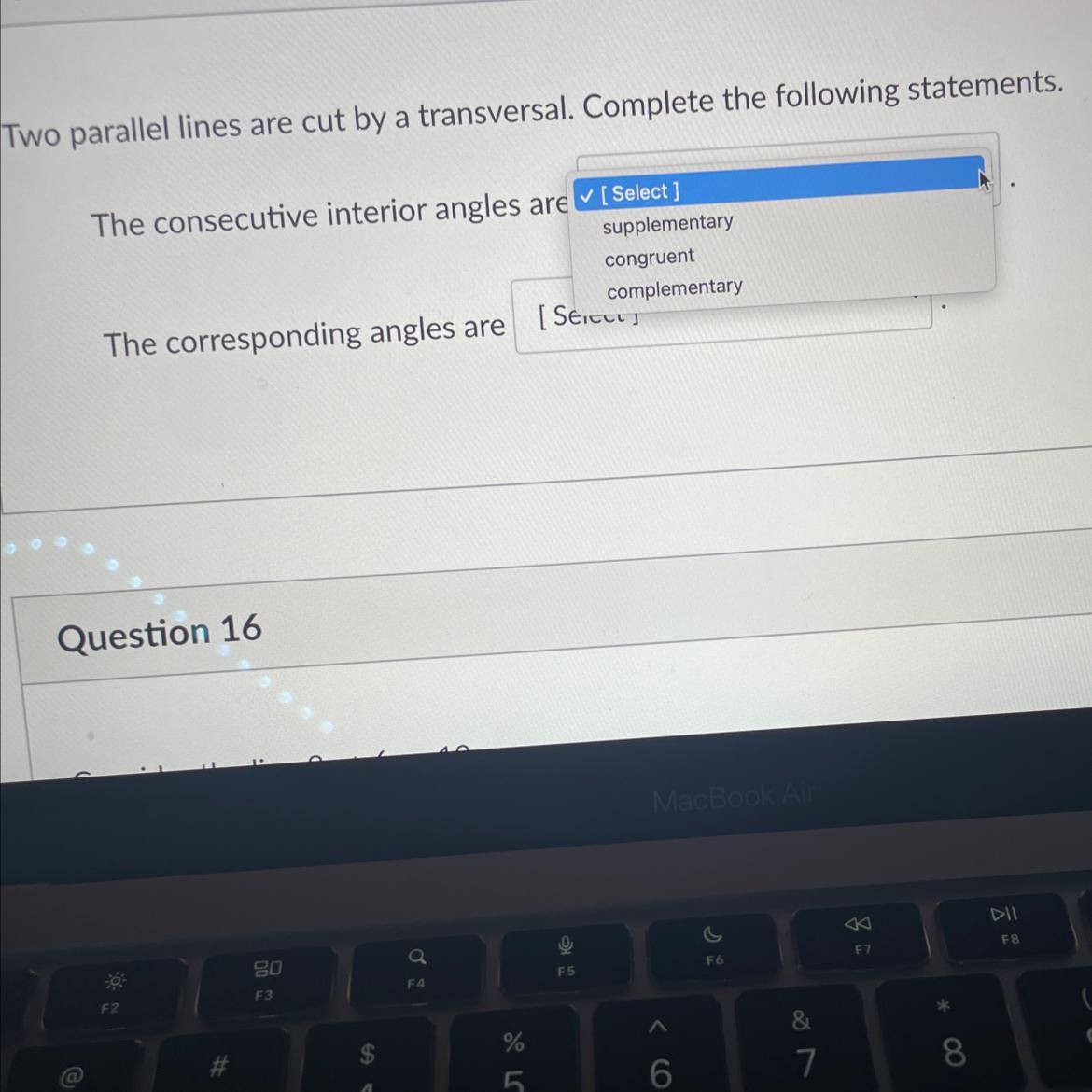
Please help me with my math. Drop downs both gave same words.
Answers
Answer:
supplementary
congruent
Step-by-step explanation:
two int angles create a line (180°) which is supplementary
corresponding angles are two angles that correspond as they are congruent
Please answer all parts of number 2.

Answers
a) false
b) true
c) true
d) true
A piecewise function is shown below. Answer Parts A-C.
Part A
What is f(-1)?
Part B
What is f(0)?
Part C
What is f(2)?
1 of 45
Answers
The value of the function is f(-3) equals -27 and f(2) equals -2.
A function is a rule that assigns each input value (x) to a unique output value (f(x)). In our case, the function f(x) = -2x² + 3x is a quadratic function because it has an x² term. To find f(-3), we substitute -3 for x in the given function:
f(-3) = -2(-3)² + 3(-3)
Now, let's solve this expression step by step:
Simplify within the parentheses first:
f(-3) = -2(9) + 3(-3)
Multiply within each set of parentheses:
f(-3) = -18 + (-9)
Add the two terms together:
f(-3) = -27
Therefore, the value of f(-3) is -27.
Similarly, to find f(2), we substitute 2 for x in the function:
f(2) = -2(2)² + 3(2)
Now, let's solve this expression step by step:
Simplify within the parentheses first:
f(2) = -2(4) + 3(2)
Multiply within each set of parentheses:
f(2) = -8 + 6
Add the two terms together:
f(2) = -2
Therefore, the value of f(2) is -2.
To know more about function here
https://brainly.com/question/28193995
#SPJ4
Complete Question:
Given f(x) = -2x²+3x find each of the following: f(-3); f(2)
a ___ is one of two pieces of a double cone divided at the vertex.
Answers
A frustum is one of two pieces of a double cone divided at the vertex. A double cone is a three-dimensional shape that is created by connecting two cones with their vertices touching.
When the double cone is cut through the vertex, it creates two pieces known as frustums. A frustum has a circular base and a smaller circular top, which are parallel to each other. The height of the frustum is the distance between the two circular bases.
The volume of a frustum can be calculated using the formula V = (1/3)h(a^2 + ab + b^2), where h is the height, a is the radius of the larger base, and b is the radius of the smaller top. Frustums are commonly found in architecture and engineering, such as in the design of buildings and bridges.
A "napped cone" is one of two pieces of a double cone divided at the vertex. When a double cone is bisected through its vertex, it results in two identical, mirror-image napped cones. These geometric shapes have various applications in mathematics, engineering, and design due to their unique properties.
Napped cones share some characteristics with regular cones, such as having a circular base, but their pointed vertex is replaced by a flat plane where the double cone was divided. This creates a shape that is both symmetrical and easy to manipulate for various purposes.
To know more about formula click here
brainly.com/question/30098455
#SPJ11
sherry had $7/8$ of a cup of sugar in her kitchen, and then she used $1/2$ of a cup of sugar to make sweet tea. she used what fraction of her sugar to make sweet tea?
Answers
Sherry used 3/8 of her sugar to make sweet tea, which is the fraction obtained by subtracting 1/2 from 7/8.
The fraction of sugar that Sherry used to make sweet tea, we need to subtract the amount of sugar she used from the total amount of sugar she had.
Sherry had $7/8$ of a cup of sugar in her kitchen, and she used $1/2$ of a cup of sugar to make sweet tea.
To find the remaining amount of sugar, we subtract $1/2$ from $7/8$:
$7/8 - 1/2$
To subtract fractions, we need a common denominator. In this case, the common denominator is 8. We can rewrite $1/2$ as $4/8$:
$7/8 - 4/8$
Now we can subtract the numerators:
$3/8$
Therefore, Sherry used $3/8$ of her sugar to make sweet tea.
To know more about fraction refer here
https://brainly.com/question/10354322#
#SPJ11
Aayan took a test and got 5/7 of the questions correct. If he got 65 questions correct, how many questions were there in the test?
Answers
Our answer of 91 questions is correct. Aayan took a test with a total of 91 questions.
To solve this problem, we can set up a proportion based on the information given and use algebra to find the total number of questions on the test.
Let's denote the total number of questions on the test as 'x'. We know that Aayan got 5/7 of the questions correct, which means he got 5/7 of the total number of questions correct.
We can set up the proportion:
(5/7) = 65/x
To solve for 'x', we can cross-multiply:
5x = 7 * 65
5x = 455
Next, we divide both sides of the equation by 5 to isolate 'x':
x = 455/5
x = 91
Therefore, there were 91 questions in the test.
To verify our answer, we can check if Aayan getting 65 questions correct is indeed 5/7 of the total number of questions.
65 is indeed 5/7 of 91:
(5/7) * 91 = 65
Therefore, our answer of 91 questions is correct. Aayan took a test with a total of 91 questions.
for more such question on total visit
https://brainly.com/question/9879870
#SPJ8