find the solution of the initial value problem. Discuss the interval of existence and provide a sketch of your solution. xy' + 2 y = sin x, y(pi/2) = 0
Answers
To solve the initial value problem xy' + 2y = sin x with y(pi/2) = 0, we can first rearrange the equation to isolate y':
y' = (sin x - 2y)/x
Then, we can use an integrating factor to solve for y:
e^(int -2/x dx) = e^(-2lnx) = 1/x^2
Multiplying both sides by the integrating factor, we get:
(1/x^2) y' - (2/x^3) y = sin x/x^2
Now, we can use the product rule to write the left side as:
d/dx (y/x^2) = sin x/x^2
Integrating both sides concerning x, we get:
y/x^2 = -cos x/x + C
Plugging in the initial condition y(pi/2) = 0, we find that C = 1/2. Therefore, the solution to the initial value problem is:
y(x) = -x/2 cos x + 1/2x^2
To find the interval of existence for this solution, we need to check if the denominator of the integrating factor (x^2) ever becomes zero. We can see that x^2 = 0 at x = 0, so the interval of existence for the solution is (-∞, 0) U (0, ∞).
Finally, we can sketch the solution by noting that it is a sum of two functions: -x/2 cos x and 1/2x^2. The first function oscillates between positive and negative values and decays to zero as x approaches infinity.
The second function is a parabola that opens upwards and goes through the point (pi/2, 0). The combination of these two functions gives a curve that starts at (0, 0), passes through (pi/2, 0), and oscillates around the x-axis as x increases or decreases.
To find the solutiontof the initial value problem, we first need to find the integrating factor for the given differential equation: xy' + 2y = sin(x), y(pi/2) = 0.
The integrating factor (IF) for this equation can be found by computing e^(∫P(x)dx), where P(x) is the coefficient of y. In this case, P(x) = 2/x, so:
IF = e^(∫(2/x)dx) = e^(2ln|x|) = |x|^2
Now, multiply the given differential equation by the integrating factor:
x^2y' + 2x*y = x^2*sin(x)
The left-hand side of the equation is now the derivative of the product (x^2*y). So, we can rewrite and integrate:
d(x^2y) / dx = x^2*sin(x)
∫(d(x^2y)) = ∫(x^2*sin(x) dx)
Unfortunately, there's no elementary function for the integral of x^2*sin(x). However, you can still analyze the interval of existence.
Given the initial condition y(pi/2) = 0 and considering the differential equation itself, there are no singularities or points that would cause the solution to not exist. Thus, the interval of existence for this initial value problem is (-∞, +∞).
As for providing a sketch, since we cannot find an elementary function for the integral, it is not possible to provide a precise graph of the solution. You may use numerical methods or software to approximate the solution graphically.
learn more about an interval of existence here: brainly.com/question/14552622
#SPJ11
Related Questions
SEE ATTACHED FOR QUESTION!!!!!!!!!!! PLS HELP ITS DUE TONIGHT!
FIND F(1)

Answers
Answer:
-6 and -3 for the dots
Step-by-step explanation:
hope this is correct im bad at math
How do I find the domain and range of y= -(x-2)^2+3?
Answers
Answer:
The domain of the expression is all real numbers except where the expression is undefined. In this case, there is no real number that makes the expression undefined. The range is the set of all valid y values.
Step-by-step explanation:
A company upgraded production machinery to transmit data to the data warehouse about the fit tolerance for assembled parts of each unit produced as the measures are taken. Before the upgrade, data was transmitted at the end of a production run. The upgrade represents an increase in
Answers
The company's upgrade in production machinery, which allows for real-time transmission of data about the fit tolerance for assembled parts of each unit produced, represents an increase in the timeliness and efficiency of data transmission.
Prior to the upgrade, data about the fit tolerance for assembled parts was transmitted at the end of a production run.
This means that the information regarding the quality and precision of the assembled parts was collected and transmitted after the entire production process was completed.
However, with the upgrade in production machinery, the company now has the capability to transmit this data in real-time as the measures are taken during the production process.
The upgrade represents an increase in the timeliness and efficiency of data transmission.
By transmitting the data in real-time, the company can immediately identify any deviations or issues in the fit tolerance of the assembled parts.
This allows for timely interventions and adjustments to be made during the production process, reducing the likelihood of producing defective or substandard units.
Real-time data transmission also enables the company to have a more accurate and up-to-date understanding of the quality of each unit produced. This information can be used for immediate feedback, quality control purposes, and process improvements.
Overall, the upgrade in production machinery enhances the company's ability to monitor and control the fit tolerance of assembled parts, leading to improved production efficiency and product quality.
Learn more about data transmission here:
https://brainly.com/question/32127477
#SPJ11
On a local swim team, 60% of the swimmers are boys. If 130 of the swimmers are girls, how many total swimmers are on the team?
Answers
Answer:
325
Step-by-step explanation:
40/100=130/x
Cross multiply to find x
40x=13000
/4 /4
x=325
What is the sum of all exterior angles of a regular octagon
Answers
Can someone help me answer this question

Answers
Answer:15 should be on the x and add all together with the 69
Step-by-step explanation:
What is 3/4 dived by 1/2
Answers
Answer:
\(\frac{3}{2}\)
Step-by-step explanation:
\(\frac{3}{4}\) ÷ \(\frac{1}{2}\)
Since we are dividing by a fraction, we switch \(\frac{1}{2}\) to it's reciprocal.
Doing that would make it \(\frac{3}{4}\) x \(\frac{2}{1}\). In other words, that is \(\frac{3}{4}\) x \(2\).
We can use cross multiplying to simplify/solve for it.
(Look at the image to see the cross multiplying).
Therefore, the answer is \(\frac{3}{2}\).

3y when y=45 ........
Answers
Answer:
\(135\)
Step-by-step explanation:
\(3y = 3 \times 45 = 135\)
Hope this helps ;) ❤❤❤
HELP : The equation r = 3c + 5 represents the values shown in the table below. c 6 8 12 18 r 23 29 ? 59 What is the missing value in the table? 12 35 41 44
Answers
Answer:
answer is 41
Step-by-step explanation:
subscribe to itzz sneaky
:the anser is
41
i just did it
The curve y=2/3 ^x³2 has starting point A whose x-coordinate is 3. Find the x-coordinate of the end point B such that the curve from A to B has length 78.
Answers
To find the x-coordinate of the endpoint B on the curve y = (2/3)^(x^3/2), we need to determine the value of x when the curve's length from point A to B is 78 units.
The length of a curve can be calculated using the arc length formula:
L = ∫[a, b] sqrt(1 + (dy/dx)^2) dx,
where a and b are the x-coordinates of the starting and ending points, respectively.
In this case, the starting point A has an x-coordinate of 3, so we can set a = 3. Let's denote the x-coordinate of the endpoint B as x_B.
To find x_B, we need to solve the following integral equation:
78 = ∫[3, x_B] sqrt(1 + (dy/dx)^2) dx.
First, let's find the derivative dy/dx:
dy/dx = d/dx ((2/3)^(x^3/2))
= (2/3)^(x^3/2) * d/dx (x^3/2)
= (2/3)^(x^3/2) * (3/2) * x^(1/2)
= (3/2) * (2/3)^(x^3/2) * x^(1/2).
Now, let's compute the integral:
78 = ∫[3, x_B] sqrt(1 + ((3/2) * (2/3)^(x^3/2) * x^(1/2))^2) dx.
Unfortunately, this integral does not have an elementary closed-form solution. We would need to use numerical methods or approximation techniques to solve it.
One common method is to use numerical integration techniques like the trapezoidal rule or Simpson's rule. These methods approximate the integral by dividing the interval [3, x_B] into smaller subintervals and approximating the function within each subinterval. By summing up these approximations, we can estimate the integral and solve for x_B.
Alternatively, if you have access to mathematical software or calculators that can perform symbolic integration, you can input the integral equation directly and solve for x_B.
learn more about integral here: brainly.com/question/31059545
#SPJ11
how many times can 19,043 go into 100
Answers
what should i do if they ask to give the answer of 2⅔×34
Answers
Answer: 272/3 OR 90.67
Step-by-step explanation:
First, turn the mixed fraction into an improper fraction. Using the times-addition method, you take the whole number (2) and multiply it by the denomitor (3). You get 6, and then add the numerator (2) to 6, getting 8, so th improper fraction of the first term is 8/3.
Then, you multiply 8/3 by 34. To do this, you do 8 times 34 divided by 3. 34 times 8 is 272, and then you divide it by 3. You don't get a whole number, so the answer could be written as 272/3 or 90.67
doess anyone know help plz

Answers
Answer:
71%
Step-by-step explanation:
The original price is 200. The dress was sold for 142.
Take the price of the dress divide the original price (142/200) then times 100.
Answer:
27% off
Step-by-step explanation:
Element X decays radioactively with a half life of 8 minutes. If there are 450 grams of Element X, how long, to the nearest tenth of a minute, would it take the element to decay to 37 grams?
Answers
If there are 450 grams of element and half life is 8 minutes, then it will take 28.83 minutes the element to decay to 37 grams
Half life of radio active element = 8 minutes
Initial quantity of radio active element = 450 gram
Final quantity of radio active element = 37 grams
y = a(0.5)^(t/h)
Substitute the values in the equation
37 = 450 (0.5)^(t/8)
Move 37 to left hand side of the equation
37 / 450 = 0.5^(t/8)
Convert the terms to logarithm
t/8 = \(log_{0.5}\frac{37}{450}\)
t/8 = 3.60
t = 8 × 3.60
Multiply the numbers
t = 28.83 minutes
Therefore, the it will take 28.83 minutes to decay to 37 grams
Learn more about half life here
brainly.com/question/4318844
#SPJ4
completed the chart for ordered pairs .Using the equation12x-8y=16x tea chart : __,0,2,__y tea chart: 0,__,__,3fil in the blanks
Answers
Given
Equation
\(12x-8y=16\)x tea chart __, 0, 2, __
y tea chart 0,__, __, 3
Procedure
y = 0
12x = 16
x = 16/12
x = 4/3
x = 0
-8y = 16
y = 16/-8
y = -2
x = 2
12(2) - 8y = 16
24 - 8y = 16
-8y = 16-24
-8y = -8
y = 1
y = 3
12x - 8(3) = 16
12x - 24 = 16
12x = 16+24
12x = 40
x = 40/12
x = 20/6
x tea chart 4/3, 0, 2, 20/6
y tea chart 0, -2, 1, 3
What are the two ratios that are equivalent to 2:9

Answers
Answer:
bc
Step-by-step explanation:
2:9 is equivalent to
18: 81 because is 2*9 : 9*9
12:54 because is 2*6 : 9* 6
What is the range of the exponential function *?
Answers
The range of exponential functions is y > 0. An exponential function's graph may be found to be strictly increasing or strictly decreasing graph.
The graph of an exponential function is found to be asymptotic to the x-axis in nature as x approaches negative infinity or as it approaches positive infinity.
An exponential function is a mathematical function which has the formula f (x) = axe, where "x" is a variable and "a" is a constant also known as the base of the function and it should be greater than zero.
The number e, which is approximately equal to 2.71828, is the most often used exponential function base.
To learn more about exponential
brainly.com/question/24427773
#SPJ4
A and C are right angles. p =
degrees.
Answers
Answer
Find out the m∠p .
To prove
As in ΔDAB is a right triangle
Apply pythagorean theorem
Hypotenuse ² = Perpendicular ² + Base²
DB² = AB² + AD²
AB = 5 units
AD = 6 units
Put in the above formula
DB² = 5² + 6²
= 25 + 36
= 61
= 7.8 units (approx)
Now in ΔDCB is a right triangle .
By using the trignometric identity .
As DC = 4 units
DB = 7.8 units (approx)
Put all the values in the trignometric identity .
∠p = 59.15 ° (approx)
Polynomial uing Remainder Theorem and Factor Theorem checking uing ynthetic diviion. X^4 - x^3 - 3x^2 4x 2 ÷ (x 2)
Answers
The remainder of the polynomial using the remainder theorem and factor theorem is 6.
Apply the remainder theorem,
When we divide a polynomial
f(x) by (x − c)
f(x) = (x − c)q(x) + r
f(c) = 0 + r
Here,
f(x)=(x−c)q(x)+rf(c)=0+r
and (x−c) is (x−(−2))
Therefore,
f(−2) = \((-2)^{4} - (-2)^3 - 3(-2)^2 + 4(-2) + 2\)
= 16 + 8 − 12 − 8 + 2
= 6
Hence, the remainder of the polynomial using the remainder theorem is 6.
Whereas using the factor theorem and doing synthetic division, we get,
x = -2 is a zero of f(x), and x+2 is a factor of f(x). To factor f(x), we divide
the coefficients of the polynomial as follows -
-2 | 1 -1 -3 4 2
-2 6 -6 4
-----------------------------------------
1 -3 3 -2 6
Hence, we get that 6 is the remainder when (\(x^4-x^3-3x^2+4x+2\)) ÷ (x+2), using the factor theorem.
Read more about factor theorem:
brainly.com/question/19030198
#SPJ4
The complete question is -
Find the remainder using the Remainder Theorem and Factor Theorem using the synthetic division of the given polynomial, \(x^4-x^3-3x^2+4x+2\) ÷ (x+2)
The manager of a clothing store is considering increasing the size of the store. She would like to determine how many square feet of space should be added in order to maximize profit. The store can be
Answers
The optimal number of square feet of space to be added is approximately 101 square feet.
We have,
To determine the optimal number of square feet of space to maximize the restaurant's profit, we need to analyze the relationship between the additional square footage, the number of new customers, and the resulting profit.
Let's start by defining some variables:
Let "x" represent the number of additional square feet of space to be added beyond the initial 100 square feet.
Let "C(x)" represent the cost in dollars to add x square feet of space. In this case, C(x) = $100 * x.
Let "N(x)" represent the number of new customers attracted per month when x square feet of space is added.
Let "P(x)" represent the profit generated per month when x square feet of space is added. In this case, P(x) = $50 * N(x).
Given the information provided, we know that each additional square foot of space attracts 2 new customers per month.
So, N(x) = 2x.
However, the number of new customers per month is expected to decrease by 1% for every 10 square feet of additional space beyond the initial 100 square feet.
To incorporate this, we can modify our equation for N(x) as follows:
N(x) = 2x * (1 - 0.01 * (x - 100) / 10)
Now, we can express the profit function P(x) in terms of x:
P(x) = $50 * N(x)
= $50 * [2x * (1 - 0.01 * (x - 100) / 10)]
= $100x * (1 - 0.01 * (x - 100) / 10)
To find the optimal number of square feet of space that maximizes profit, we need to find the value of x that maximizes P(x).
We can do this by taking the derivative of P(x) with respect to x, setting it equal to zero, and solving for x.
dP(x)/dx = $100 * (1 - 0.01 * (x - 100) / 10) + $100x * (-0.01 / 10)
= $100 - $1 * (x - 100) + $100x * (-0.01 / 10)
= $100 - $1x + $100 * (-0.01 / 10) - $1x
= $100 - $2x - $0.01x + $10x
= $100 + $7x - $0.01x
Setting dP(x)/dx equal to zero:
$100 + $7x - $0.01x = 0
$7x - $0.01x = -$100
0.99x = $100
x ≈ $100 / 0.99
x ≈ 101.01
Since we're dealing with square footage, we can round the result to the nearest whole number.
Therefore,
The optimal number of square feet of space to be added is approximately 101 square feet.
Learn more about derivatives here:
https://brainly.com/question/29020856
#SPJ4
The complete question:
The manager of a restaurant is considering expanding the seating area. She wants to determine how many additional square feet of space should be added to maximize the restaurant's profit. The cost to add new space is $100 per square foot, and the profit generated per square foot is estimated to be $50 per month. The manager expects that each additional square foot of space will attract 2 new customers per month. However, the number of new customers per month is expected to decrease by 1% for every 10 square feet of additional space beyond the initial 100 square feet.
What is the optimal number of square feet of space that should be added to maximize the restaurant's profit?
What is wrong with this solution?
( PLEASE HELP :(
Please and thank you
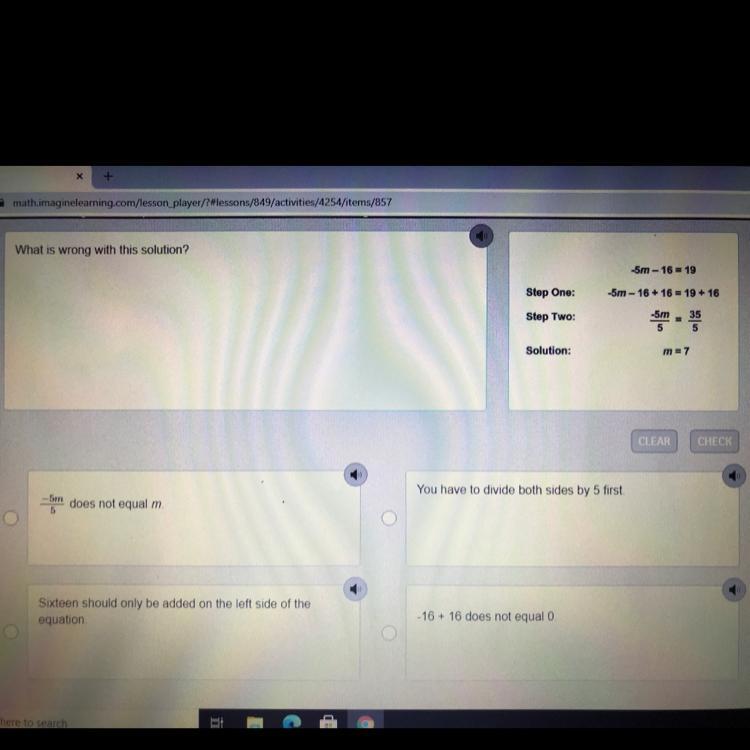
Answers
Answer:
−5m/5 does not equal m.
Step-by-step explanation:
Evaluate this exponential expression. 6•(4+2)^2-3^2
Answers
Answer: 207
I hope you get it right
Jack has a bag of candy full of 3 strawberry chews and 17 cherry chews that he eats one at a time. Which word or phrase describes the probability that he reaches in without looking and pulls out a cherry chew?
Answers
Answer:
seventeen out of twenty
Step-by-step explanation:
The phrase that describes this probability would be
seventeen out of twenty
This is because the bag has a total of 20 candies ( 3 strawberry chews and 17 cherry chews). If he randomly chooses one from the bag, he has a 17/20 chance of getting a cherry chew because there are 17 total cherry chews in the bag. If we were to change this fraction into a phrase it would be the phrase above in bold.
144 is what percent of 240?
Percent Proportion-
Percent Equation-
Answers
Answer: 60 %
Step-by-step explanation:
To find what percent 144 is of 240, we can use the following proportion:
part/whole = percent/100
Let x be the percentage we are trying to find, then we can write:
144/240 = x/100
To solve for x, we can cross-multiply:
14400 = 240x
Dividing both sides by 240, we get:
x = 14400/240 = 60
Therefore, 144 is 60% of 240.
Answer:
60%
Step-by-step explanation:
Percent proportion:
240 - 100%
144 - x%
Cross-multiply to find x:
\( \frac{144 \times 100\%}{240} = \frac{14400}{240} = 60\%\)
So, 144 is 60% of 240
Triangle SAM is congruent to Triangle REN. Find x and y.

Answers
\(\measuredangle A\cong \measuredangle E\implies 112=16x\implies \cfrac{112}{16}=x\implies \boxed{7=x} \\\\[-0.35em] ~\dotfill\\\\ \overline{MS}\cong \overline{NR}\implies 41=3x+5y\implies 41=3(7)+5y\implies 41=21+5y \\\\\\ 20=5y\implies \cfrac{20}{5}=y\implies \boxed{4=y}\)
A certain culture of the bacterium Rhodobacter sphaeroides initially has 25 bacteria and is observed to double every 6 hours. (a) Find an exponential model n(t) = n02t/a for the number of bacteria in the culture after t hours.
Estimate the number of bacteria after 13 hours. (Round your answer to the nearest whole number.)
After how many hours will the bacteria count reach 1 million? (Round your answer to one decimal place.)
Answers
Since the culture is observed to double every 6 hours, we know that the growth rate is constant at r = ln(2)/6 per hour.
To calculate growth rates, divide the difference between the starting and ending values for the period under study by the starting value. The most frequent time intervals for growth rates are annually, quarterly, monthly, and weekly.
We can use the formula for exponential growth to model the number of bacteria in the culture after t hours:
n(t) = n0e^(rt)where n0 is the initial number of bacteria.
Substituting in the values given in the problem, we get:
n(t) = 25e^[(ln(2)/6)t]Simplifying this expression using the properties of logarithms, we can rewrite it in the form:
n(t) = 25(2)^(t/6)This is the exponential model for the number of bacteria in the culture after t hours.
To know more about growth rate visit:
https://brainly.com/question/23879811
#SPJ4
The exponential model for population of bacteria, \(n(t) = n_0{2}^{\frac{t}{a} }\) can be written \(n(t) = 25 \times {2}^{\frac{t}{6} }\) for the number of bacteria in the culture after t hours. The estimate number of bacteria after 13 hours is equals to the 112. In 92 hours, the bacteria count will reach to 1 million.
We have a certain culture of the bacterium Rhodobacter.
Initial population, n₀ = 25
The population become doubles in every 6 months. The exponential model
\(n(t) = n_0{2}^{\frac{t}{a} }\) for the number of bacteria in the culture after t hours. Now, the population become double in 6 hours, so a = 6 , then exponential equation is \(n(t) = 25 \times {2}^{\frac{t}{6} }\).
We have to estimate the number of bacteria after 13 hours. That is t = 13 hours, \(n( t) = 25( 2)^{\frac{t}{6}}\)
Substitute t = 13 hours
\( = 25( 2)^{\frac{13}{6}}\)
\(= 25( 2)^{2.16}\)
= 111.728713807 ~ 112
So, n(13) = 112
We have to determine the value of t in hours for n(t) = 1 million = 1000000, using the above equation, \(1000000 = 25( 2)^{\frac{t}{6}}\)
\(40000 = ( 2)^{\frac{t}{6}}\)
Taking natural logarithm both sides
=>\( ln( 40000) = ln(( 2)^{\frac{t}{6}})\)
=> \(ln(40000) = \frac{t}{6} ln(2)\)
=> \(t = \frac{6 ln( 40000)}{ ln(2)}\)
= 91.7262742773 ~ 92
Hence, required value is 92 hours..
For more information about exponential model, visit:
https://brainly.com/question/29527768
#SPJ4
Please answer Question #4 within an hour.
4. Pipelining: [8] a. What is pipelining, and what is its purpose? [4] b. What is the theoretical speedup in a system that uses pipelining? [4]
Answers
Pipelining is a technique that breaks down a complex task into smaller, simpler tasks that can be performed in parallel. This allows the computer to complete the task more quickly than if it were to perform the task sequentially.
Pipelining is a common technique used in computer architecture. It is a way of breaking down a complex task into smaller, simpler tasks that can be performed in parallel. This allows the computer to complete the task more quickly than if it were to perform the task sequentially. For example, consider the task of adding two numbers. This task can be broken down into the following smaller tasks:
Fetch the first number from memory.
Fetch the second number from memory.
Add the two numbers together.
Store the result in memory.
If these tasks were performed sequentially, the computer would have to wait for each task to complete before it could start the next task. This would take a long time. However, if these tasks were performed in parallel, the computer could start working on the next task as soon as the previous task was finished. This would allow the computer to complete the task much more quickly.
The theoretical speedup in a system that uses pipelining is equal to the number of stages in the pipeline. The theoretical speedup in a system that uses pipelining is equal to the number of stages in the pipeline. This is because each stage in the pipeline can be working on a different task at the same time. For example, consider a system with a pipeline that has four stages. The first stage could be fetching the first number from memory, the second stage could be fetching the second number from memory, the third stage could be adding the two numbers together, and the fourth stage could be storing the result in memory.
If all four stages were working at the same time, the system could complete the task of adding two numbers in one-fourth of the time it would take if the task were performed sequentially. In practice, the actual speedup in a system that uses pipelining is less than the theoretical speedup. This is because there are some overheads associated with pipelining, such as the time it takes to switch from one stage to the next. However, pipelining is still a very effective way to improve the performance of a computer system.
Learn more about pipelining here:- brainly.com/question/23932917
#SPJ11
Use the following notations: r = radius of a circle, v = linear velocity, w = angular velocity. Find the missing quantity. Round to the nearest tenth if necessary. V= 1235 m/min, r = 65 m, w = ?
Answers
The angular velocity of the circle is approximately 19 m/s.
In order to find the missing quantity, we can use the relationship between linear velocity and angular velocity in a circle. The linear velocity of a point on the edge of a circle is the product of the radius and the angular velocity. This can be expressed as:
v = r * w
where v is the linear velocity, r is the radius, and w is the angular velocity.
To find the value of w, we can rearrange this equation to solve for w:
w = v / r
Substituting the given values of v and r, we get:
w = 1235 m/min / 65 m
w = 19 m/s
It's important to note that units must be consistent when using formulas to solve problems. In this case, we converted the given linear velocity from m/min to m/s before plugging it into the formula. Also, we rounded the answer to the nearest tenth, as instructed, since the given values were rounded to the nearest unit.
To learn more about angular velocity
https://brainly.com/question/29557272
#SPJ4
Math help due soon thanks

Answers
Answers:
SkippingSee the diagram belowx = 7No they are not similar=======================================
Explanation:
SkippingWe peel the triangles apart as shown below. There's not much to say about it. The only thing I can think is that the larger horizontal side is 8+6 = 14 m.Due to the similar triangles, we can form the proportion x/4 = 14/8. The 14 is from 8+6. Cross multiplying leads to 8x = 56 which solves to x = 7.Focus on the triangle on the left. The missing angle is 180-95-35 = 50 degrees. The missing angle for the triangle on the right is 180-35-60 = 85 degrees. The angles don't all match up, so the triangles aren't similar.
Cecil sold vegetables at the farmers market on Saturday and Sunday. On Saturday, he collected twenty $1 bills, six $5 bills, four $10 bills, and five $20 bills. On Sunday, he collected thirty $1 bills, four $5 bills, five $10 bills, and one $20 bill. How much money did Cecil collect in total?
Answers
Answer:
$250.00
Step-by-step explanation:
twenty $1 bills- 20 x 1 = 20
six $5 bills- 6 x 5 = 30
four $10 bills- 4 x 10 = 40
five $20 bills- 5 x 20 = 100
thirty $1 bills- 30 x 1 = 30
four $5 bills- 4 x 5 = 20
five $10 bills- 5 x 10 = 50
one $20 bill- 1 x 20 = 20
Add the bold totals together and get the final answer of $250.00