find the surface area of a cylinder with a height of 20 inches and base radius of 7 inches
Answers
As, we have :
Height of cylinder, h = 20 inchesRadius of cylinder, r = 7 inchesTo find surface area, we have a formula :
\( \Large \underline{\boxed{\tt{Surface \: Area = 2\pi rh+2 \pi r^{2}}}}\)
By filling values :
\( \sf : \implies Surface \: Area = 2 \pi (7)(20)+2 \pi (7)^{2}\)
\( \sf : \implies Surface \: Area = 280 \pi + 2 \pi (7)(7)\)
\( \sf : \implies Surface \: Area = 280 \pi + 98 \pi\)
Now, put value of π = 22/7
\( \sf : \implies Surface \: Area = 280\times \dfrac{22}{7} + \cancel{98} \times \dfrac{22}{\cancel{7}}\)
\( \sf : \implies Surface \: Area = 40 \times 22 + 14 \times 22\)
\( \sf : \implies Surface \: Area = 40 \times 22 + 14 \times 22\)
\( \sf : \implies Surface \: Area = 880 + 308\)
\( \sf : \implies Surface \: Area = 1188\)
\( \Large \underline{\boxed{\tt{Surface \: Area = 1188 \: inches^{2} }}}\)
Hence, Surface area of given cylinder is 1188 inches².
Answer:
A≈1187.52in²
Step-by-step explanation:
A=2πrh+2πr2=2·π·7·20+2·π·72≈1187.52202in²
Hope it helps
Related Questions
Find the area of the surface generated when the given curve is revolved about the given axis. 4sqrtx
Answers
The area of the surface generated by revolving the curve about the x-axis is 9664π / 3 square units.
Given: The equation of the curve is y = 4√x on [21,77]
The formula for finding the surface area of a curve rotated about the x-axis on some interval [a, b] is given by:
\(S = \int\limits^b_a {2\pi f(x)\sqrt{1 +(f'(x))^{2} } } \, dx\)
where S is the surface area,
f(x) is y
a and b is the given interval such that a ≤ x ≤ b or [a, b]
Now in this question,
f(x) = 4√x
a = 21, b = 77
f'(x) = 4 * 1 / 2√x = 2 / √x
f'(x) = 2 /√x
Placing the respective values in the equation we get,
\(S = \int\limits^{77}_{21} {2\pi. 4\sqrt{x} \sqrt{1+(\frac{2}{\sqrt{x} } )^{2} } } \, dx\)
\(S = 8\pi\int\limits^{77}_{21} {\sqrt{x} \sqrt{1+\frac{4}{x} } } \, dx\)
\(S = 8\pi\int\limits^{77}_{21} {\sqrt{x} * \frac{\sqrt{x + 4} }{\sqrt{x} } } \, dx\)
\(S = 8\pi\int\limits^{77}_{21} {\sqrt{x+4} } } \, dx\)
we know the formula for the integral
\(\int\limits^b_a {\sqrt{ax + b} } \, dx = \frac{2}{3a}(ax+b)^{\frac{3}{2} } | { {{b} \atop {{a}}} \right.\)
Therefore, by applying the formula, we get:
\(S = 8\pi *\frac{2}{3}(x+4)^{\frac{3}{2} } | { {{77} \atop {{21}}} \right.\)
\(S = \frac{16\pi }{3} \{ (77+4)^{\frac{3}{2}} - (21+4)^{\frac{3}{2} }\}\)
\(S = \frac{16\pi }{3} \{ (81)^{\frac{3}{2}} - (25)^{\frac{3}{2} }\}\)
\(S = \frac{16\pi }{3} \{729 - 125\}\)
\(S = \frac{16\pi }{3} * 604\)
\(S = \frac{9664\pi }{3}\)
Hence, The area of the surface generated by revolving the curve about the x-axis is 9664π / 3 square units
Know more about "surface area generated by revolving curve" here: https://brainly.com/question/24132132
#SPJ4
Disclaimer: The given question is incomplete. The complete question is mentioned below:
Find the area of the surface generated when the given curve is rotated about the x-axis y= 4sqrt(x) on [21,77]
The area of the surface generated by revolving the curve about the x-axis is ___ square units (type an exact answer, using pi as needed)
Halp.
What is the ratio of the sides from the big to the small rectangle?

Answers
Answer:
2:1
Step-by-step explanation:
We know
To get from F to G, we have to go from -2 to 2, for which the length is 4.
To get from F' to G', we have to go from -2 to 0, for which the length is 2.
What is the ratio of the sides from the big to the small rectangle?
The ratio is 4:2 = 2:1
SOMEONE HELPPP PLZ!!!

Answers
In a savings canister, Tom has a total of $2.85 in pennies and quarters. If the number of pennies Tom has in 5 more than three times thee number of quarters , how many pennies and quarters does he have in the can
Answers
Answer:
$69 i think im not smart
Step-by-step explanation:
cube with a side length of 12 centimeters is filled with water. A stone that just fits into the cube is
emerged into it, displacing some of the water. The stone is nearly spherical. Once the stone is remove
m the cube, how much water remains in the cube? Approximate your answer to the nearest tenth usit
The amount of water remaining is ______ cubic centimeters
Answers
Answer:
823.7
Step-by-step explanation:
b. Can an objective function P=a x+b y+c have (the same) maximum value at all four vertex points Q, R, S , and T ? At points R and S only? Explain using examples.
Answers
No, an objective function P=a x+b y+c can not have the same maximum value at all four vertex points Q, R, S, and T. The objective function P can have the same maximum value at points R and S only.
Explanation: This is because, for a linear programming problem, there are multiple constraints, which form the feasible region for the problem.
For a 2-dimensional linear programming problem, the feasible region is a convex polygon whose vertices are the intersection points of the constraint lines.
In a feasible region, the maximum or minimum value of the objective function is always attained at one of the vertex points or along one of the boundary lines.
The vertex points are the most important points as they are the only points that provide the extreme values of the objective function.
In the given problem, if the objective function P = a x + b y + c has the same maximum value at all four vertex points Q, R, S, and T, then it means that the objective function is parallel to all four sides of the feasible region. This is not possible as the feasible region is a convex polygon.
Therefore, the objective function can have the same maximum value at points R and S only. For example, consider the following feasible region and the objective function P = 3x + 2y.The vertex points of the feasible region are A(0,4), B(2,2), C(4,0), and D(0,0).
At vertex points B and C, the objective function P has the same maximum value of 10.
Therefore, the objective function P can have the same maximum value at points R and S only.
For more such questions on objective function
https://brainly.com/question/25828237
#SPJ8
Solve the given differential equation:
xy''+y'=0
usually if it was the form (x^2)y''+xy'+5y=0, you could then assume (r^2)+(1-1)r+5=0
how do i start/solve this?
Answers
The solution to the given differential equation is \(y = a_0x^{[0]} + a_1x^{[1]} + a_2x^{[2]}\), where a_0, a_1, and a_2 are constants.
How to solve the differential equationTo fathom the given differential equation, xy'' + y' = 0, we will begin by expecting a control arrangement of the frame y = ∑(n=0 to ∞) a_nx^n, where a_n speaks to the coefficients to be decided.
Separating y with regard to x, we get:
\(y' = ∑(n=0 to ∞) a_n(nx^[(n-1))] = ∑(n=0 to ∞) na_nx^[(n-1)]\)
Separating y' with regard to x, we get:
\(y'' = ∑(n=0 to ∞) n(n-1)a_nx^[(n-2)]\)
Presently, we substitute these expressions for y and its subsidiaries into the differential condition:
\(x(∑(n=0 to ∞) n(n-1)a_nx^[(n-2))] + (∑(n=0 to ∞) na_nx^[(n-1))] =\)
After improving terms, we have:
\(∑(n=0 to ∞) n(n-1)a_nx^[(n-1)] + ∑(n=0 to ∞) na_nx^[n] =\)
Another, we compare the coefficients of like powers of x to zero, coming about in a boundless arrangement of conditions:
For n = 0: + a_0 = (condition 1)
For n = 1: + a_1 = (condition 2)
For n ≥ 2: n(n-1)a_n + na_n = (condition 3)
Disentangling condition 3, we have:
\(n^[2a]_n - n(a_n) =\)
n(n-1)a_n - na_n =
n(n-1 - 1)a_n =
(n(n-2)a_n) =
From equation 1, a_0 = 0, and from equation 2, a_1 = 0.
For n ≥ 2, we have two conceivable outcomes:
n(n-2) = 0, which gives n = or n = 2.
a_n = (minor arrangement)
So, the solution to the given differential equation is \(y = a_0x^{[0]} + a_1x^{[1]} + a_2x^{[2]}\), where a_0, a_1, and a_2 are constants.
Learn more about differential equations here:
https://brainly.com/question/28099315
#SPJ1
Reed Hopkins purchased 350 shares of Barber Industries at $11. 93 per share. Recently the company paid annual dividends of $0. 10 per share. What were his annual dividends? What is the annual yield?
Answers
Reed Hopkins received annual dividends of $35.00 and the annual yield was 0.84%.
Reed Hopkins purchased 350 shares of Barber Industries at $11.93 per share, for a total cost of $4,175.50. The company paid annual dividends of $0.10 per share, so Reed received 350 x $0.10 = $35.00 in annual dividends. To calculate the annual yield, we divide the annual dividends by the total cost of the investment and multiply by 100%. Thus, the annual yield is ($35.00 / $4,175.50) x 100% = 0.84%.
Learn more about dividends here
https://brainly.com/question/25845157
#SPJ11
Solve the following equation.
-p/12 =6
Answers
The solution to the equation is p = -72.
The equation, we need to isolate the variable 'p' on one side of the equation. Let's go through the steps:
-p/12 = 6
To get rid of the fraction, we can multiply both sides of the equation by 12:
12 * (-p/12) = 12 * 6
This simplifies to:
-p = 72
To isolate 'p,' we can multiply both sides of the equation by -1:
(-1) * (-p) = (-1) * 72
This gives us:
p = -72
Therefore, the solution to the equation is p = -72.
To learn more about equation
brainly.com/question/29657983
#SPJ11
The length of a rectangle is two more than two times its width. The perimeter of the rectang
52m. What is the area of the rectangle?
A
144 in2
B
18 in2
С
26 in2
D
8 in2
Answers
Answer:
a
Step-by-step explanation:
plss help me with this

Answers
Answer:
Below in bold.
Step-by-step explanation:
7x - 2 + 9x - 2 + 2(5x) = 2(5x + 5) + 2(4x)
7x + 9x + 10x - 4 = 10x + 10 + 8x
7x + 9x + 10x - 10x - 8x = 10 + 4
8x = 14
x = 14/8 = 7/4
So, ST = 5*7/4 + 5
= 55/4
= 13 3/4
Answer:
ST = 13.75
Step-by-step explanation:
The perimeter of a trapezium is calculated with the following formula:
P = a + b + c + d (a, b: bases, c, d: sides)
The perimeter of a rectangle is calculated with the following formula:
P= 2(a + b) (a: base, b: side)
we will write the following equation to find the length of ST
7x - 2 + 9x - 2 + 5x + 5x = 2(5x + 5 + 4x) first do the inside the parenthesis
2(9x + 5) = 18x + 10
Now,
7x - 2 + 9x - 2 + 5x + 5x = 18x + 10 add like terms on the left side of the equation
26x - 4 = 18x + 10 transfer like terms to the same side of the equation
26x - 18x = 10 + 4 add/subtract
8x = 14 divide both sides by 8
x = 1.75 replace x with this to calculate the lentgh of ST
5x + 5 = 5*(1.75) + 5 and ST = 13.75
The selling price of each cup of lemon juice is 3/2 times as much as the selling price of a cup of apple juice. For every 2 cups of lemon juice sold, Mr Tan sells 5 cups of apple juice. He earns $12 more from apple juice than from lemon juice. How much does Mr Tan earn altogether?
Answers
Therefore , the solution of the given problem of unitary method comes out to be Mr. Tan makes a total of $30 Plus $18 = $48.
An unitary method is what?To finish the job using the unitary technique, the equation from this nano section should be multiplied by two. In essence, when a wanted object is present, both the characterised by either a group and the pigment sections are omitted from the unit method. A variable fee of Inr ($1.01), for instance, would be paid for 40 pens. It's conceivable that one nation will have complete control over the strategy used to achieve this. Almost all living things have a unique trait.
Here,
Let's name the CDs' pre-tax cost "x" for simplicity. The overall cost of the CDs before tax is two times because Lena purchased two of them for the same price. The cost of the Discs, with the addition of the $1.80 sales tax, is:
=> 2x + $1.80
Given that we know the final price, including tax, was $23.40, we can create the following equation:
=> 2x + $1.80 = $23.40
By deducting $1.80 from each half, we arrive at:
=> 2x = $21.60
When you divide both parts by 2, you get:
=> x = $10.80
As a result, each Disc cost $10.80 before taxes.
We can create another equation now that we know his revenues from selling apple juice are $12 higher than his profits from selling lemon juice:
=> 30n - 18n = 12
=> 12n = 12
=> n = 1
As a result, Mr. Tan sells 2n + 5n = 7n = 7 glasses of juice, for a total profit of 30n = $30 from the sale of apple juice and 18n = $18 from the sale of lemon juice.
Therefore, Mr. Tan makes a total of $30 Plus $18 = $48.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
Tutorial Exercise cylindrical tank with radius 6 m is being filled with water at a rate of 3 m3/min_ How fast is the height of the water increasing (in m/min)? Step Let represent the radius of the cylindrical tank in m, let h represent the height of the water in the tank in m; and let V represent the volume of the water in the tank in m3 . Writing an equation for V in terms of and h gives the following result: We are given that the radius of the tank is 6 m, and therefore the radius of the column of water that is being measured remains at a constant 6 Substituting the value 6 into the volume equation gives a simplified equation for V in terms of h, as follows_ V =
Answers
The height of the water increasing at the rate of \(\frac{1}{12} \frac{m}{min}\) .
What is a function?
In mathematics, a function is a unique arrangement of the inputs (the domain) and their outputs (the codomain), where each input has exactly one output and the output can be linked to the input.
We need a function to connect the two variables when there are associated rates; in this instance, it is unmistakably volume and height. The equation is:
\(V=\) \(\pi r^{2}h\)
Although radius is mentioned in the formula, it is not a variable in this issue because it is constant. We might change the value in
V=\(\pi(6m)^{2}h\)
We must implicitly differentiate wrt (with respect to) time because the rate in this problem is tied to time
\(\frac{dV}{dt} =(36m^{2} )\) \(\pi\frac{dh}{dt}\)
In the problem, we are given \(3\frac{m^{2} }{min}\) which is \(\frac{dV}{dt}\) .So we substitute this in:
\(\frac{dh}{dt} =\frac{3m^{3}}{min(36m^{2} )\pi }\)
\(=\frac{3}{36\pi} \frac{m}{min}\)
\(=\frac{1}{12} \frac{m}{min}\)
Hence, the height of the water increasing at the rate of \(\frac{1}{12} \frac{m}{min}\) .
To learn more about rate related questions;
https://brainly.com/question/119866
#SPJ4
Anyone out there can solve this I will give 17 points!!!
Lauren is twice Kristy’s age. The sum of Lauren and Kristy’s ages is 51. Which equation represents the sum of their ages?
A K + K + 2 = 51 B K + 2K + 2 = 51 C 2K = 51 D K + 2K = 51
Answers
Answer:
D. K+2K=51
Step-by-step explanation:
Since Lauren is 2 times Kristy's age, Lauren's age=2K
so, if the sum of the two is 51, then 2K+K=51
If you want to solve it, 2K+K=3K=51
51/3=K
17=K
34=L
Answer:
D K + 2K = 51
Step-by-step explanation:
Lauren is twice Kristy's age so it would be 2K cause you want to multi[ly, and then you have to add Kristy's age in the equation because their ages added together is 51
differentiate 4/9 with respect to , assuming that is implicitly a function of . (use symbolic notation and fractions where needed. use ′ in place of . )
Answers
Note that the use of the term "implicitly" in the question suggests that there is some other equation or context that defines y, but without that information, we can only assume that y is an arbitrary function. To differentiate 4/9 with respect to an implicitly defined function, we first need to clarify what that function is.
Let's call it y, so we have: 4/9 = f(y)
Now, we can differentiate both sides with respect to y using the chain rule: d/dy (4/9) = d/dy (f(y))
0 = f'(y)
So, the derivative of 4/9 with respect to an implicitly defined function y is 0. We can write this as:
d/dy (4/9) = 0
Note that the use of the term "implicitly" in the question suggests that there is some other equation or context that defines y, but without that information, we can only assume that y is an arbitrary function.
Learn more about differentiation here, https://brainly.com/question/954654
#SPJ11
An animal shelter conducts an annual fundraising drive. The animal shelter must raise at least enough money to cover their annual rental of $2,500 and weekly expenses of $450. So far, the shelter has received a one-time donation of $125 and pledged donations of $680 per week. Which inequality can be used to find w, the number of weeks it can take for the shelter to meet the goal?
Answers
The inequality that can be used to find w, the number of weeks it can take for the shelter to meet its goal, is: w ≥ 10
To find the inequality that can be used to determine the number of weeks it can take for the animal shelter to meet its fundraising goal, we need to consider the total expenses and donations.
Let's break down the expenses and donations:
Expenses:
Annual rental = $2,500
Weekly expenses = $450
Donations:
One-time donation = $125
Pledged donations per week = $680
Let w represent the number of weeks it takes for the shelter to meet its goal.
Total expenses for w weeks = Annual rental + Weekly expenses * w
Total expenses = $2,500 + $450w
Total donations for w weeks = One-time donation + Pledged donations per week * w
Total donations = $125 + $680w
To meet the goal, the total donations must be greater than or equal to the total expenses. Therefore, the inequality is:
Total donations ≥ Total expenses
$125 + $680w ≥ $2,500 + $450w
Simplifying the inequality, we have:
$230w ≥ $2,375
Dividing both sides of the inequality by 230, we get:
w ≥ $2,375 / $230
Rounding the result to the nearest whole number, we have:
w ≥ 10
Therefore, the inequality that can be used to find w, the number of weeks it can take for the shelter to meet its goal, is:
w ≥ 10
Learn more about number from
https://brainly.com/question/27894163
#SPJ11
\(2xy + -3(xy) x=10 y=-5
Answers
\(\text{Plug in and solve:}\\\\2(10)(-5) + -3(10(-5))\\\\2(-50) + -3(10(-5))\\\\2(-50) + -3(-50)\\\\-100+ -3(-50)\\\\-100+150\\\\\boxed{50}\)
2³-2"=29
n=
Find the value of n
Answers
Answer:
\(2 + 2 + 2 - 2 = 29\)
Using the Equation, predict how much the Temperature change will be in 20 years since 2000.
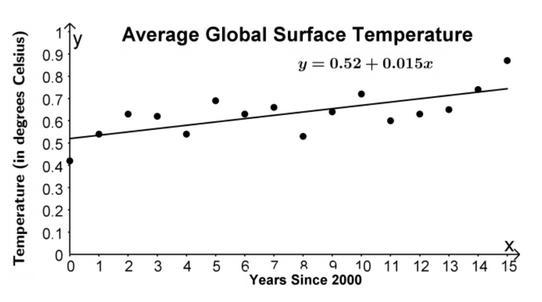
Answers
Answer:
0.82° C
Step-by-step explanation:
To predict how much change the temperature will be in 20 years time since 2000, simply substitute x = 20 into the given equation, \( y = 0.52 + 0.015x \):
\( y = 0.52 + 0.015(20) \)
\( y = 0.52 + 0.3 \)
\( y = 0.82 \)
✅The temperature change would be 0.82° C.
you measure 27 backpacks' weights, and find they have a mean weight of 52 ounces. assume the population standard deviation is 7.7 ounces. based on this, construct a 95% confidence interval for the true population mean backpack weight
Answers
95% confident that the true population mean backpack weight falls between 49.06 and 54.94 ounces.
To construct a 95% confidence interval for the true population mean backpack weight, we can use the following formula:
Confidence interval = mean weight ± (critical value x standard error)
Where the critical value is determined based on the level of confidence and the degrees of freedom (n-1), and the standard error is calculated as the population standard deviation divided by the square root of the sample size.
In this case, since we have a sample size of 27, the degrees of freedom would be 26. Using a t-distribution table, we can find the critical value for a 95% confidence level with 26 degrees of freedom to be 2.056.
The standard error can be calculated as:
standard error = 7.7 / sqrt(27) = 1.48
Therefore, the 95% confidence interval can be calculated as:
Confidence interval = 52 ± (2.056 x 1.48) = (49.06, 54.94)
This means that we can be 95% confident that the true population mean backpack weight falls between 49.06 and 54.94 ounces, based on the sample of 27 backpacks with a mean weight of 52 ounces and a population standard deviation of 7.7 ounces.
Visit here to learn more about confidence interval brainly.com/question/13067956
#SPJ11
There are black and white counters in a bag in the ratio 20:17
There are 54
more black counters than white counters.
How many black counters are there?
Answers
There are 360 black counters and 306 white counter in 20:17 ratio.
Let's denote the number of black counters by B and the number of white counters by W. We know that the ratio of black to white counters is 20:17, which means that:
B/W = 20/17
We also know that there are 54 more black counters than white counters, which means that:
B = W + 54
We can use substitution to solve for B. Substituting the second equation into the first equation, we get:
(W + 54)/W = 20/17
Cross-multiplying, we get:
17(W + 54) = 20W
Expanding the left side, we get:
17W + 918 = 20W
Subtracting 17W from both sides, we get:
918 = 3W
Dividing both sides by 3, we get:
W = 306
Now we can use the second equation to find B:
B = W + 54 = 306 + 54 = 360
Therefore, there are 360 black counters in the bag.
To learn more about ratio click here
brainly.com/question/13419413
#SPJ4
Help me!!
2. pts) Set up a proportion and soive for
side TV (y):

Answers
The required measure of side y = 8
Given : Triangle TUV and triangle XWV are similar
Thus \(\frac{UV}{VW} = \frac{6}{21}\)
this is further equal to \(\frac{2}{7}\)
Thus the ratio UV : VW = 2 : 7
this implies that the ratio TV : VX should also be equal to the ratio of UV : VW = 2 : 7 because of cpst or also called corresponding parts of similar triangles.
Given UV : VW = 2 : 7
thus TV : VX = \(\frac{y}{28 }\) which on equation will give y as 8
because \(\frac{8}{28}\) when divided by 4 will give us the required ratio that is 2 : 7
To know more about similar triangles or related problems you may visit the link which is mentioned below:
https://brainly.com/question/25882965
#SPJ1
which expressions can we use to describe how many more seconds tatenda spends than ciara spends mowing lawns during 4 weeks?
Answers
The expression used to calculate how many more seconds Tatenda spends than Ciara spends mowing lawns during 4 weeks is 4(700t- 750c) .
What is an expression in math example?
2x + 3 is an illustration of a mathematical expression with a variable. Each and every variable needs to have a coefficient, or a value multiplied by the variable. The number 2 is the coefficient of x in the formula 2x + 3, which indicates 2 times x plus 3.time taken by tatenda to mow a square meter of lawn = t seconds
time taken by Ciara to mow a square meter of lawn = c seconds
area mowed by tatenda in a week = 700 square meters
area mowed by Ciara in a week = 750 square meters
the expression used to calculate how many more seconds Tatenda spends than Ciara spends mowing lawns during 4 weeks
time taken by tatenda for mowing in 4 weeks = 4 * 700 * t seconds
time taken by Ciara for mowing in 4 weeks = 4 * 750 * c seconds
more seconds Tatenda spends than Ciara spends mowing lawns during 4 weeks = [4 * 700 * t ] - [4 * 750 * c]
= 4(700t- 750c)
Therefore, the expression used to calculate how many more seconds Tatenda spends than Ciara spends mowing lawns during 4 weeks is 4(700t- 750c).
Learn more about mathematical expression
brainly.com/question/14462529
#SPJ4
A student collect data about a toy motorized airplane.
Mass = 4 kg
Time = 3 sec
Height = 5 meters
Velocity = 2 m/sec
Gravity acceleration = 10 m/sec2
What is the potential energy?
Answers
Answer:
PEg = 196.2 J
Step-by-step explanation:
PEg = mass * gravitational field* height
PEg = 4kg * 9.81m/s² * 5m
PEg = 196.2 kg m²/s²
Applying cost-benefit analysis, a business should only purchase a large machine if the business can pass the cost of the machine onto consumers O projects sales growth based on the machine's use estimates that the machine's cost is less than the revenue it will generate assigns a high utility to the machine based on consumer perceptions O has enough financial capital to replace the machine in five years Jasmine owns a farm and sells produce to local restaurants and grocery stores. If her farm is perfectly competitive, what profits and losses can she expect to make in the short and in the long run? Jasmine may earn economic profits or losses in the short run and in the long run. Jasmine may earn zero economic profit in the short run and profits in the long run. Jasmine may earn zero economic profit in the short run and losses in the long run. Jasmine may earn economic profits or losses in the long run but not in the short run Jasmine may earn economic profits or losses in the short run but not in the long run. Suppose the price elasticity of demand for widgets is 2 and the price of widgets decreases by 10 percent. The change in quantity demanded of widgets must O increase by 5 percent O decrease by 5 percent O increase by 20 percent O decrease by 20 percent O decrease by 200 percent Use the table to answer the question that follows. Number of Units Produced Average Total Cost 1 9 10 2 3 12 4 15 5 16 What is the marginal cost of the third unit produced? O $12 O $16 o $24 $36 Indeterminate
Answers
The marginal cost of the third unit produced is $21.
How to calculate the marginal costThe average total cost (ATC) is calculated by dividing the total cost (TC) by the number of units produced. From the given table, we can see that when two units are produced, the average total cost is $12.
In order to find the total cost of producing two units, we multiply the average total cost by the number of units: $12 × 2 = $24.
Now, let's move on to the total cost of producing three units. We are given that the average total cost when three units are produced is $15. Therefore, the total cost of producing three units is $15 × 3 = $45.
The change in total cost between producing two units and three units is $45 - $24 = $21.
Finally, we divide the change in total cost by the change in quantity produced to find the marginal cost of the third unit: $21 ÷ (3 - 2)
= $21.
Learn more about marginal cost on
https://brainly.com/question/17230008
#SPJ1
the cost for an upcoming field trip is 20 dollars the cost of the feild trip c is a function of the number of students x select all the possible outputs for the function defined by c(x)=20x
Answers
20 is the possible outputs for the function defined by c(x)=20x for all of the students that would pay for the field trip
How to solve for the functionThe function that is known to represent what would be the cost of the trip of these students is given as C(x)=20x.
The cost of the trip for one of the students is put at 20 dollars each.
We would have x as the total number of those that would be attending this trip. In order to get the output that would show us the cost of the trip.
We take X to be a whole number.
then x = 1
such that that c(1) = 20(1) = 20
Then the total is 20 per student
Read more on cost functions here:https://brainly.com/question/2292799
#SPJ1
the cost for an upcoming field trip is 20 dollars the cost of the feild trip c is a function of the number of students x select all the possible outputs for the function defined by c(x)=20x
A 20 B 30 c 50
WuT this
2[18 -(5 + 3 to the 2nd power) ÷ 7]
Answers
Answer:
32
Step-by-step explanation:
2[18 -(5 + 9) ÷7]
2[18 -14 ÷7]
2[18 -2]
2[16]
32
Given that angle A = 30 degrees, side a = 10ft, and side b =
8ft, find the remaining sides and angles of the triangle if they
exist.
Answers
The remaining sides and angles of the triangle are side c ≈ 18.47 ft, angle B ≈ 23.58 degrees, and angle C ≈ 126.42 degrees.
To find the remaining sides and angles of the triangle given that angle A = 30 degrees, side a = 10ft, and side b = 8ft, we need to determine if the given information represents a valid triangle. Since we have one angle and two sides, we can use the Law of Sines.
The Law of Sines states that (a/sinA) = (b/sinB) = (c/sinC), where a, b, and c are the sides of the triangle, and A, B, and C are the corresponding angles.
Step 1: Use the given information to find angle B.
(10/sin(30)) = (8/sinB)
10/sin(30) = 8/sinB
10/0.5 = 8/sinB
20 = 8/sinB
sinB = 8/20
sinB = 0.4
B = arcsin(0.4)
Angle B ≈ 23.58 degrees
Step 2: Find angle C.
Since the sum of angles in a triangle is 180 degrees:
C = 180 - (A + B)
C = 180 - (30 + 23.58)
C ≈ 126.42 degrees
Step 3: Find side c using the Law of Sines.
(10/sin(30)) = (c/sin(126.42))
10/0.5 = c/sin(126.42)
20 = c/sin(126.42)
c ≈ 20 * sin(126.42)
c ≈ 18.47 ft
So, the remaining sides and angles of the triangle are side c ≈ 18.47 ft, angle B ≈ 23.58 degrees, and angle C ≈ 126.42 degrees.
Learn more about triangles here: brainly.com/question/2773823
#SPJ11
Find the SURFACE AREA of the
cylinder below.
10 yd radius and 15 yd height. (ROUND TO NEAREST TENTH)
Answers
Answer:
1571
Step-by-step explanation:
its 1570.8 but you have to round
HELP DUE TODAY!! WILL GIVE BRAINLY TO RIGHT ANSWER

Answers
Answer:
sin x = 8/ POcos y = 8/ POStep-by-step explanation:
sin = opposite leg / hypotenuse
cos = adjacent leg / hypotenuse
sin x = 8/ POcos y = 8/ PORatios are same