find the TSA of a Cylinder with a radius of 17 cm and height 5 cm
Answers
Answer:
The TSA of a cylinder is equal to 2πr2 + 2πrh, where r is the radius and h is the height.
In this case, the TSA is equal to 2π(17 cm)2 + 2π(17 cm)(5 cm) = 2π(289 cm2) + 2π(85 cm2) = 2π(374 cm2).
Answer:
approximately 2349.842cm^2
Step-by-step explanation:
the formula for TSA of the cylinder is 2pi r(r+h)
(I'm taking the value of pi to be 3.1415)
2(3.1415)(17)(17+5)
=2,349.842cm^2 and that's the answer
Related Questions
I need some help I will give you brainiest.
A teaspoon of common table salt contains about 2,000 mg of sodium. How many grams of sodium is this?
200 g
2 g
2,000,000 g
20 g
Answers
kim has identical lamps and identical tables. how many ways are there for her to put all the lamps on the tables?
Answers
Kim can arrange the 10 identical lamps on the 3 identical tables in 66 different ways.
Number of lamps= 10
Number of tables=3
For identical objects we have the following formula;
(n + r - 1)C(r - 1) (r - 1)
We thus have;
n + r - 1 = 10 + 3 - 1
= 12
r - 1 = 3 - 1
= 2
Thus,
(n + r - 1)C(r - 1) = ¹²C₂
Apply the following combination formula:
ⁿCr = n!/((n - r)!r!)
So, we have:
¹²C₂ = 12!/((12 - 2)! * 2!)
¹²C₂ = 12!/(10! * 2!)
¹²C₂ = 12 * 11 * 10!/(10! * 2!)
¹²C₂ = 132/2
= 66
Therefore, there are 66 ways to put all the lamps on the tables.
To learn more about combinations visit;
https://brainly.com/question/28065038
#SPJ4
How do I solve line functions?
Answers
A linear function is one that begins with f{x} followed by the rest of the equation that respects the slope intercept form of an equation
i need help fast pls

Answers
Answer:
positive numbers show deposits so it'd be A! $126.40
100 points! Mhanifa can you please help? Look at the picture attached. I will mark brainliest!

Answers
Answer:
1 and 2.
Midpoints calculated, plotted and connected to make the triangle DEF, see the attached.
D= (-2, 2), E = (-1, -2), F = (-4, -1)3.
As per definition, midsegment is parallel to a side.
Parallel lines have same slope.
Find slopes of FD and CB and compare.
m(FD) = (2 - (-1))/(-2 -(-4)) = 3/2m(CB) = (1 - (-5))/(1 - (-3)) = 6/4 = 3/2As we see the slopes are sameFind the slopes of FE and AB and compare.
m(FE) = (-2 - (- 1))/(-1 - (-4)) = -1/3m(AB) = (1 - 3)/(1 - (-5)) = -2/6 = -1/3Slopes are sameFind the slopes of DE and AC and compare.
m(DE) = (-2 - 2)/(-1 - (-2)) = -4/1 = -4m(AC) = (-5 - 3)/(-3 - (-5)) = -8/2 = -4Slopes are same4.
As per definition, midsegment is half the parallel side.
We'll show that FD = 1/2CB
FD = \(\sqrt{(2+1)^2+(-2+4)^2}\) = \(\sqrt{3^2+2^2}\) = \(\sqrt{13}\)CB = \(\sqrt{(1 + 5)^2+(1+3)^2}\) = \(\sqrt{6^2+4^2}\) = 2\(\sqrt{13}\)As we see FD = 1/2CBFE = 1/2AB
FE = \(\sqrt{(-4+1)^2+(-1+2)^2}\) = \(\sqrt{3^2+1^2}\) = \(\sqrt{10}\)AB = \(\sqrt{(-5 -1)^2+(3-1)^2}\) = \(\sqrt{6^2+2^2}\) = 2\(\sqrt{10}\)As we see FE = 1/2ABDE = 1/2AC
DE = \(\sqrt{(-2+1)^2+(2+2)^2}\) = \(\sqrt{1^2+4^2}\) = \(\sqrt{17}\)AC = \(\sqrt{(-5 +3)^2+(3+5)^2}\) = \(\sqrt{2^2+8^2}\) = 2\(\sqrt{17}\)As we see DE = 1/2AC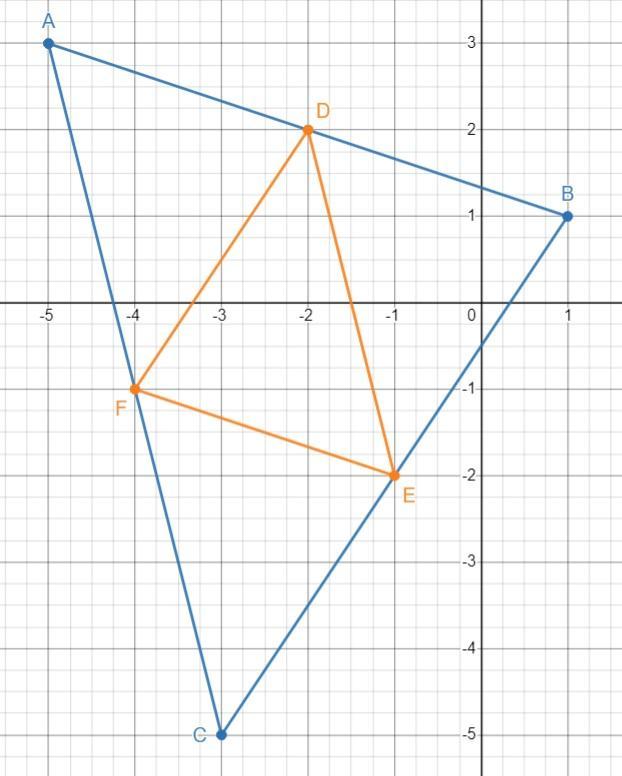
A hardware store was charging $4.51 for a screwdriver but raised the price 17%. The new price after the increase is $5.28. Enter an expression to show how the new price was calculated.
please help asap! This is for a test and I need it to raise my grade.
Answers
.7667 PLUS (you are adding because there was a RAISE if 17%) 4.51 gets you 5.2767 which is later rounded to get 5.28!
Please name Brainliest I want to level up!!
b. 14 divided by 5/6
Answers
Answer:
16.8 or 16 whole 4/5
Step-by-step explanation:
14 divided by 5/6
take reciprocal
14 x 6/5
84/5
16.8
Stating that the area under the standard normal distribution curve between z=0 and z=1.00 is 0.3413, is the same as stating that the __________ of randomly selecting a standard normally distributed variable z with a value between 0 and 1.00 is 0.3413
Answers
Stating that the area under the standard normal distribution curve between z=0 and z=1.00 is 0.3413, is the same as stating that the probability of randomly selecting a standard normally distributed variable z with a value between 0 and 1.00 is 0.3413.
Simply put, the probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes. Statistics is the study of events that follow a probability distribution.
In science, the probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%. The more likely it is that the event will occur, the higher its probability.
Therefore, the given statement is completed as:
Stating that the area under the standard normal distribution curve between z=0 and z=1.00 is 0.3413, is the same as stating that the probability of randomly selecting a standard normally distributed variable z with a value between 0 and 1.00 is 0.3413.
Learn more about probability:
https://brainly.com/question/13604758
#SPJ11
Which expression is an equivalent expression of 12x + 10 + 4y?
OA. 2(6x + 2y + 6)
OB. 3(4x + y + 10)
OC. 2(6x + 4y+8)
OD. 2(6x + 5 + 2y)
Please help me TwT
Answers
Answer:
D. 2(6x + 5 + 2y)
Step-by-step explanation:
You have to use the distributive property to get your answer. 2 × 6x = 12x; 2 × 5 = 10; 2 × 2y = 4y.
Need help now.
Someone please.

Answers
Answer:
$1,075
Step-by-step explanation:
Simple Intereat Formula:
A = P(1+rt)
where A is the final amount,
P is the principal(original amount invested)
r = annual interest rate
t = time in years
Given P = 1000
r = 2.5/100
t = 3 (Beginning of 4th year means the 4th year is not counted)
A = 1000(1+(0.025)(3))
= 1000(1.075)
=$1,075
if i have a 74.23% in math class and i get a 0 on a Summative Assignment, what is my new grade?
Y'all are smart, please help
Answers
find the values of a,b,and c

Answers
Answer:
a = 1
b = -6
c = 0
Hope this helps!
Answer:
a = 1
b = -6
c = 0
Step-by-step explanation:
A standard quadratic equation is set up in the form ax^2+bx+c. So, for this equation, "a" is the value before the x^2, which is 1, "b" is the value before the x, which is -6, and since there is no "c" value, that means c is 0.
i rllly need this one pls help

Answers
The slope of the line is 2.
We are given a graph with coordinate axes, namely, the x-axis and the y-axis.The intersection of the coordinate axes is called the origin with coordinates (0, 0).The line is drawn in blue.The line passes through two dots, whose coordinates can be found using the graph.The coordinates of the points are (1, 1) and (-1, -3).The slope "m" of a line passing through points (x1, y1) and (x2, y2) is calculated as :m = (y2-y1)/(x2-x1)The slope of the line shown in the graph is :m = (-3-1)/(-1-1)m = -4/-2m = 2Thus, the slope of the line is 2.To learn more about slope, visit :
https://brainly.com/question/3605446
#SPJ1
what is cross products
Answers
Which of the following correlation coefficients represents the strongest relationship between two variables? -.75 +.60 .00 +.30
Answers
The correlation coefficient that represents the strongest relationship between two variables is -0.75.
In correlation coefficients, the absolute value indicates the strength of the relationship between variables. The strength of the association increases with the absolute value's proximity to 1.
The maximum absolute value in this instance is -0.75, which denotes a significant negative correlation. The relevance of the reverse correlation value of -0.75 is demonstrated by the noteworthy unfavorable correlation between the two variables.
To know more about correlation coefficients, visit,
https://brainly.com/question/4219149
#SPJ4
1. (From the textbook, 5.1(a)). Does the following production function exhibit constant returns to scale? Y
t
=A[αK
t
v
v−1
+(1−α)N
t
v
v−1
]
v−1
v
Answers
The production function Yt =A[αK tv v−1+(1−α)N tv v−1] v−1v does not exhibit constant returns to scale.
What is constant returns to scale?The concept of constant returns to scale is a property of production functions. It refers to a situation in which an increase in inputs such as labor, capital, or both results in a proportionate rise in output.
How to determine whether a production function has constant returns to scale?The production function Y = f(K, N) exhibits constant returns to scale if, for all values of K and N, there is a scalar λ such that Y(λK, λN) = λY(K, N)
If this condition holds, then we can say that the production function exhibits constant returns to scale.
Does the production function Yt =A[αK tv v−1+(1−α)N tv v−1] v−1v exhibit constant returns to scale?
Let us determine whether the production function
Yt =A[αK tv v−1+(1−α)N tv v−1] v−1v
exhibits constant returns to scale using the definition above.
Y(λK, λN) = A[α(λK) v (v−1) + (1−α)(λN) v (v−1)] v−1vY(λK, λN)
Y(λK, λN) = A[λvαK v (v−1) + λv(1−α)N v (v−1)] v−1vY(λK, λN)
Y(λK, λN) = A[λvαK v (v−1)v−1v + λv(1−α)N v (v−1)v−1v]Y(λK, λN)
Y(λK, λN) = λvA[αK v−1 + (1−α)N v−1] v
Since λ appears outside the bracket, the production function does not satisfy the condition of constant returns to scale because λ is not eliminated on both sides of the equation.
Therefore, we can conclude that the production function Yt =A[αK tv v−1+(1−α)N tv v−1] v−1v does not exhibit constant returns to scale.
Learn more about the production function from the given link-
https://brainly.com/question/33503247
#SPJ11
help me with this question pleaseee
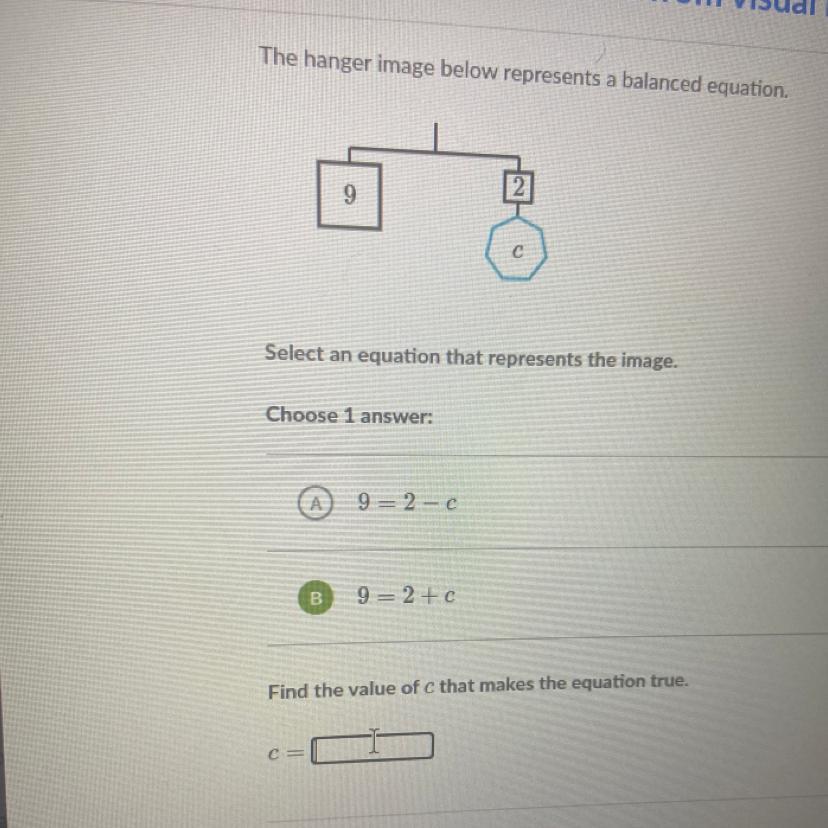
Answers
What is the circumference of a circle with a diameter of 4.2 cm?
Answers
Answer:
it would be C≈13.19cm
hope this helps :)
In the coordinate plane, line p has slope 8 and y-intercept (0, 5). Line r is the result of dilating line p by a factor of 3 with center (0, 3). What are the slope and y-intercept of line r?.
Answers
In the given coordinate plane, based on the given dilation the line r has slope 8 and coordinate (0,8)
Dilation:
Dilation refers the ratio of the given line to line by the scale factor.
Given
In the coordinate plane, line p has slope 8 and y-intercept (0, 5). Line r is the result of dilating line p by a factor of 3 with center (0, 3).
Here we need to find the the slope and y-intercept of line r.
Here we know that scale factor is 3.
Let us consider the slope of the line r will not change and the intercept is the addition of their ordinate will be.
So, it can be written as,
=> Intercept = 5 + 3
=> Intercept = 8
Therefore, the line r has slope 8 and coordinate (0.8).
To know more about Dilation here.
brainly.com/question/11911650
#SPJ4
The article "Scrambled Statistics: What Are the Chances of Finding Multi-Yolk Eggs?"† gives the probability of a double-yolk egg as 0. 1. (a) Give a relative frequency interpretation of this probability. In the long run, about % of eggs are double-yolk. (b) If 5,000 eggs were randomly selected, about how many double-yolk eggs would you expect to find? eggs Need Help? Read It
Answers
a) A relative frequency interpretation of the probability of a double-yolk egg being 0.1 is that, in the long run or over a large number of eggs, approximately 10% of eggs will have double yolks.
b) If 5,000 eggs were randomly selected, we can estimate the number of double-yolk eggs we would expect to find by multiplying the probability of a double-yolk egg (0.1) by the total number of eggs (5,000).
Expected number of double-yolk eggs = 0.1 * 5,000 = 500 eggs.
a) The probability of a double-yolk egg being 0.1 can be interpreted as the relative frequency of finding double-yolk eggs over a large number of eggs. It means that if we were to select a significant number of eggs, approximately 10% of them would have double yolks. This interpretation is based on the assumption that the eggs are randomly selected and the probability remains constant.
b) To estimate the number of double-yolk eggs in a sample of 5,000 eggs, we can use the probability given in the article. By multiplying the probability of a double-yolk egg (0.1) by the total number of eggs (5,000), we can calculate the expected number of double-yolk eggs. In this case, the expected number would be 500 eggs. This means that, on average, we would expect to find 500 double-yolk eggs out of the 5,000 eggs randomly selected. It is important to note that this is an expected value based on probability, and the actual number of double-yolk eggs found may vary in any given sample.
To learn more about probability
brainly.com/question/31828911
#SPJ11
Please help me nowww!

Answers
Answer:
3:1
Step-by-step explanation:
The squirrel tore up 3 of the sleeping bags and one was left untouched.
In an AP, a1,a2,a3,.....an, where a1 represents first term and an represents nth term, what is the common difference d?
Answers
Answer:
a2 - a1
Step-by-step explanation:
Tn= a+(n-1)d
Tn = a1 (an -1) a2-a1
Persevere adam, ben, and charlie each formed a different 4-digit number using all the digits, 1, 2, 6, and o. adam and charlie both rounded their numbers to the nearest hundred. ben rounded his number to the nearest ten. ben and charlie had the same answer while adam's answer was 100 less than theirs. find the 4-digit number each boy formed. show your work
Answers
The probability Adam chose the number 1260, Ben chose 1260, and Charlie also chose 1260. Adam's number was rounded to 1200, Ben's to 1260, and Charlie's to 1300, making Adam's number 100 less than the other two.
Adam:
(1*1000) + (2*100) + (6*10) + (0*1)
= 1200
Ben:
(1*1000) + (2*100) + (6*10) + (0*1)
= 1260
Charlie:
(1*1000) + (2*100) + (6*10) + (0*1)
= 1300
Adam, Ben, and Charlie each chose the 4-digit number 1260, but rounded it differently. Adam rounded it to the nearest hundred, giving him an answer of 1200. Ben rounded it to the nearest ten, giving him the same answer of 1260. Charlie rounded it to the nearest hundred, giving him an answer of 1300. Thus, Adam's answer was 100 less than the other two.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
CAN SOMEONE PLS HELP WITH THIS ASAP!!
Answers
Answer:
What is it?
Step-by-step explanation:
what is the greatest common factor between 20 and 25
Answers
Answer:
5
Step-by-step explanation:
Brian's plane departs from the airport at 11:00 a.m. He need to be there 2 hours before his plane takes off. What time does Brian arrive at the airport?
Answers
. Consider a configuration model with degree distribution Pk = Ckak, where a and C are positive constants and a < 1. (a) Calculate the value of the constant C as a function of a. (b) Calculate the mean degree of the network. (c) Calculate the mean-square degree of the network. (d) Hence, or otherwise, find the value of a that marks the phase transition between the region in which the network has a giant component and the region in which it does not. Does the giant component exist for larger or smaller values than this? You may find the following sums useful in performing the calculations: kak =- a T 12, a + a2 kok - a + 4a2 +03 19 (1-a2' (1-a3 (1-a4 k=0 k=0 k=0
Answers
(a) The value of the constant C is calculated as C = 1 / (∑k=1 to ∞(ak)).
(b) The mean degree of the network is given by the expression μ = ∑k=1 to ∞(kPk).
(a) To calculate the constant C, we need to determine the value of the sum ∑k=1 to ∞(ak). Using the provided expression, we find C = 1 / (∑k=1 to ∞(ak)).
(b) The mean degree of the network is calculated by multiplying each degree k by its corresponding probability Pk and summing up these values for all possible degrees. The expression for the mean degree is μ = ∑k=1 to ∞(kPk).
(c) The mean-square degree of the network is calculated similarly to the mean degree, but with the square of each degree. The expression for the mean-square degree is μ2 = ∑k=1 to ∞(k^2Pk).
(d) The phase transition between the region with a giant component and the region without occurs when the giant component emerges. This happens when the value of a is such that the equation 1 - aμ = 0 is satisfied. Solving this equation for a will give us the value that marks the transition. The giant component exists for values of a smaller than this critical value.
Note: The provided sums (∑k=0 to ∞(ak), ∑k=0 to ∞(a^2k), ∑k=0 to ∞(a^3k), ∑k=0 to ∞(a^4k)) may be helpful in performing the calculations involved in the expressions for C, μ, and μ2
Learn more about mean degree here:
https://brainly.com/question/10110884
#SPJ11
Solve the initial value problemf’(x) = 1/x - 2x + x^1/2; f(4) = 2

Answers
SOLUTION:
Case: Initial value problem
An initial value problem is an ordinary differential equation together with an initial condition that specifies the value of the unknown function at a given point in the domain
To solve the initial value problem, we have a value of the derivative of y when x is known.
y'(x)= value
Given:
f(4)=2
\(\begin{gathered} f^{\prime}(x)=\frac{1}{x}-2x+x^{\frac{1}{2}} \\ Integrating \\ f(x)=ln(x)-\frac{2x^2}{2}+\frac{2x^{\frac{3}{2}}}{3}+C \\ f(x)=ln(x)-x^2+\frac{2x^{\frac{3}{2}}}{3}+C \\ f(4)=2 \\ f(4)=ln(4)-2(4)^2+\frac{2(2)^{\frac{3}{2}}}{3}+C \\ 2=1.386-32+1.8856+C \\ C=2-1.3863+32-1.8856 \\ C=30.7281 \end{gathered}\)The resulting equation will be:
\(f(x)=\ln x-x^2+\frac{2x^{\frac{3}{2}}}{3}+30.7281\)Final answer:
\(f(x)=\operatorname{\ln}x-x^2+\frac{2x^{\frac{3}{2}}}{3}+30.7281\)P=-3(n-500)2 + 950 000
Answers
Answer:
n = - p - 950,000/6 + 500
Step-by-step explanation:
5. Let A={0,3,4,5,7} and B={4,5,6,7,8,9,10,11}. Let D be the divides relation. That is, for all (x,y)∈A×B,xDy iff x∣y. a) Write the relation set D and draw the relation diagram with arrows. b) Write the relation set D−1, the inverse relation of the relation D and draw the relation diagram with arrows.
Answers
a) The relation set D is {(0,4), (0,5), (0,7), (3,6), (3,9), (4,4), (4,8), (4,12), (5,5), (5,10), (5,15), (7,7), (7,14)}. The relation diagram with arrows can be drawn as follows:
0 → 4, 5, 7
3 → 6, 9
4 → 4, 8, 12
5 → 5, 10, 15
7 → 7, 14
b) The relation set D-1 is {(4,0), (5,0), (7,0), (6,3), (9,3), (4,4), (8,4), (12,4), (5,5), (10,5), (15,5), (7,7), (14,7)}. The relation diagram with arrows can be drawn as follows:
4 → 0, 4, 8, 12
5 → 0, 5, 10, 15
7 → 0, 7, 14
6 → 3
9 → 3
8 → 4
12 → 4
10 → 5
15 → 5
14 → 7
a) The relation set D consists of pairs (x, y) such that x ∈ A and y ∈ B, and x divides y. D = {(0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 9), (0, 10), (0, 11), (3, 6), (3, 9), (4, 4), (4, 8), (5, 5), (5, 10), (7, 7)}. In the relation diagram, draw arrows from elements of A to elements of B according to these pairs.
b) The inverse relation set D⁻¹ consists of pairs (y, x) such that x ∈ A and y ∈ B, and x divides y. D⁻¹ = {(4, 0), (5, 0), (6, 0), (7, 0), (8, 0), (9, 0), (10, 0), (11, 0), (6, 3), (9, 3), (4, 4), (8, 4), (5, 5), (10, 5), (7, 7)}. In the relation diagram, draw arrows from elements of B to elements of A according to these pairs.
Visit here to learn more about relation set brainly.com/question/10831286
#SPJ11