Find the unit rate. 7/8 square foot in 1/4 hour.Enter the correct answer in the box.
Answers
To find the unit rate of 7/8 square foot in 1/4 hour, we can proceed as follows:
\(\frac{\frac{7}{8}}{\frac{1}{4}}=\frac{7}{8}\cdot4=\frac{28}{8}=\frac{14}{4}=\frac{7}{2}=3.5\)The unit rate is, therefore, 3.5 square foot an hour or
3.5 ft^2/hour.
Related Questions
What is x3+3x2−16x−48 divided by x+3
Answers
Answer:
x² - 6x + 2, and the remainder is -54
Step-by-step explanation:
I have attached an image of me dividing it.

Find the area of each figure in square units pls pls pls help ☝️

Answers
Answer:
24u^2
Step-by-step explanation:
Divide the figure into two quad-l's.
5x4
2x2
------
20
4
-----
24
-----
The answer is 24 units squared.
Hope this helped!
change to exponential form
(4√ x5)
Answers
n√x=x1n(4√5)5=(514)5
Now, use this rule of exponents to combine the exponents:
(xa)b=xa×b(514)5=514×5=554
p=1/4q+8 make q the subject
Answers
Answer:
q = 4p - 32
Step-by-step explanation:
P = 1/4q + 8
Making q the subject
P - 8 = 1/4q
Divide both sides by 1/4
q = (p - 8) ÷ 1/4
= (P - 8) × 4/1
= 4p - 32
q = 4p - 32
Mark charges a one-time fee of $12 for travel and then $7.50 per hour for labor. How
many hours will he need to work to make $42?
A.3
B.4
C.5
D.6
Answers
Answer:
$42
Step-by-step explanation:
D
In the accompanying diagram ACE, BCD, and AB || DE. if AC=2, CD=6, and CE=3, what is the length of BC.

Answers
Answer:
BC = 4
Step-by-step explanation:
The the ratio for the corresponding sides of the two triangles would be equal. Therefore:
6/x = 3/2
Cross multiply
x*3 = 2*6
3x = 12
3x/3 = 12/3
x = 4
✅BC = x = 4
O
Tom wants to pour 84.99 grams of salt into a container. So far, he has poured. 17.4 grams. How much more salt should Tom pour?
grams
Explanation
Check
X
G
Eple Charter
Answers
The remaining amount of salt that Tom needed to pour was 67.59 grams.
What is subtraction?To subtract in mathematics is to take something away from a group or a number of objects.
In other meaning, subtraction is a mathematical operation such that two values are going to subtract and give a resultant value.
The group's total number of items decreases or becomes lower when we subtract from it.
As per the given,
The total amount that Tom needs to pour = 84.99 grams
Amount poured = 17.4 grams
Remaining = 84.99 grams - 17.4 grams = 7.59 grams
Hence "The remaining amount of salt that Tom needed to pour was 67.59 grams".
For more about subtraction,
https://brainly.com/question/1927340
#SPJ1
Find the domain of fg f(x) = x + 2 g(x) =1/x + 2
Answers
Answer:
x+2 domain: (-infiniy, +infinity) or -infinity<x<infinity
1/x +2 domain: (-infinity, 0) and (0, infinity) or 0<x<0
pls i need it now
thx i might gv brainliest

Answers
The total pay that Nelly will get for last week is £220.
What will the total pay of Nelly be ?From the information given, the following can be deduced:
£8 per hour for the first 15 hours
£10 let hour for any extra hour.
The above are applicable for Monday to Friday.
£16 is the rate for Saturdays.
The number of hours that Nelly worked from Monday to Friday will be:
= 3 1/2 + 5 + 2 1/2 + 4 + 2
= 17 hours
On Saturday, he worked 5 hours.
The total earnings will be:
= (£8 × 15) + (£10 × 2) + (£16 × 5)
= £120 + £20 + £80
= £220
The total amount is £220.
Learn more about income on:
brainly.com/question/28390284
#SPJ1
At the park there is a pool shaped like a circle with diameter 24 yd. A ring-shaped path goes around the pool. Its width is 6 yd.
We are going to give a new layer of coating to the path. If one gallon of coating can cover 5 yd^2, how many gallons of coating do we need? Note that coating comes only by the gallon, so the number of gallons must be a whole number. (Use the value 3.14 for pi.)

Answers
The number of gallons must be a whole number will be 114 gallons.
What is the area of the circle?Let d be the diameter of the circle. Then the area of the circle will be
A = (π/4) d² square units
At the recreation area, there is a pool molded like a circle with a measurement of 24 yds. A ring-molded way circumvents the pool. Its width is 6 yds.
The area of the path will be given as,
A = (π/4) (24 + 6 + 6)² - (π/4) (24)²
A = (π/4) [36² - 24²]
A = (π/4) [720]
A = 565.5 square yards
We will give another layer of covering to the way. On the off chance that one gallon of covering can cover 5 yd². Then the number of gallons of coating is given as,
⇒ (565.5) / 5
⇒ 113.097
⇒ 114 gallons
The number of gallons must be a whole number will be 114 gallons.
More about the area of a circle link is given below.
https://brainly.com/question/11952845
#SPJ1
A three-digit personal identification number is chosen using the digits 1-9. The digits cannot be repeated.
What is the approximate probability that the first digit will be 6?
Answers
Answer
1/9
Step-by-step explanation:
Hope this helps
Answer:
0.11111111111
Step-by-step explanation:
1/9 = 0.11111111111
Assume you have a safe code that is 8 digits long. The numbers 0-9 may be used for any digit. How many possible codes are there? Show your work and leave your answer in either exponential or factorial form.
Answers
Answer:
10^8 choices
Step-by-step explanation:
You have 10 numbers to choose from for each digit of the code.
There are 8 digits of the code.
You have 10*10*10*10*10*10*10*10 = 10^8 choices in total.
Number of possible codes are \(10^{8}\)
What is Permutation?In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements
Given,
Number of digits in passcode = 8
The numbers 0-9 may be used for any digit. Therefore total of 10 numbers
Here repetition is allowed.
Therefore, each of the 8 vacant place can be filled in the succession of 10 different ways
Number of possible codes are = 10×10×10×10×10×10×10×10 = \(10^{8}\)
Hence, the number of possible codes are \(10^{8}\)
Learn more about Permutation here
https://brainly.com/question/1216161
#SPJ2
Find all solutions to 6x^4+13x^3–71x^2+67x=15
Answers
Answer:
x = 1 or x = 3 / 2 or x = −5 or x = 1 / 3
Refer the attachment for steps
Hope it helps
Please mark me as the brainliest
Thank you

Hove
Find the average rate of change indicated below.
y = 4x+1
[-1, 1)
A.15
B.3.75
C.1.875
D.7.5
Answers
The average rate of change of the function over the interval is 4
Finding the average rate of changeFrom the question, we have the following parameters that can be used in our computation:
y = 4x + 1
The interval is given as
[-1, 1)
The function is a linear function
This means that it has a constant average rate of change
From y = 4x + 1, we have
Rate = 4
Hence, the rate is 4
Read more about average rate of change at
https://brainly.com/question/17131025
#SPJ1
Can you please show me the steps to double check my answer?
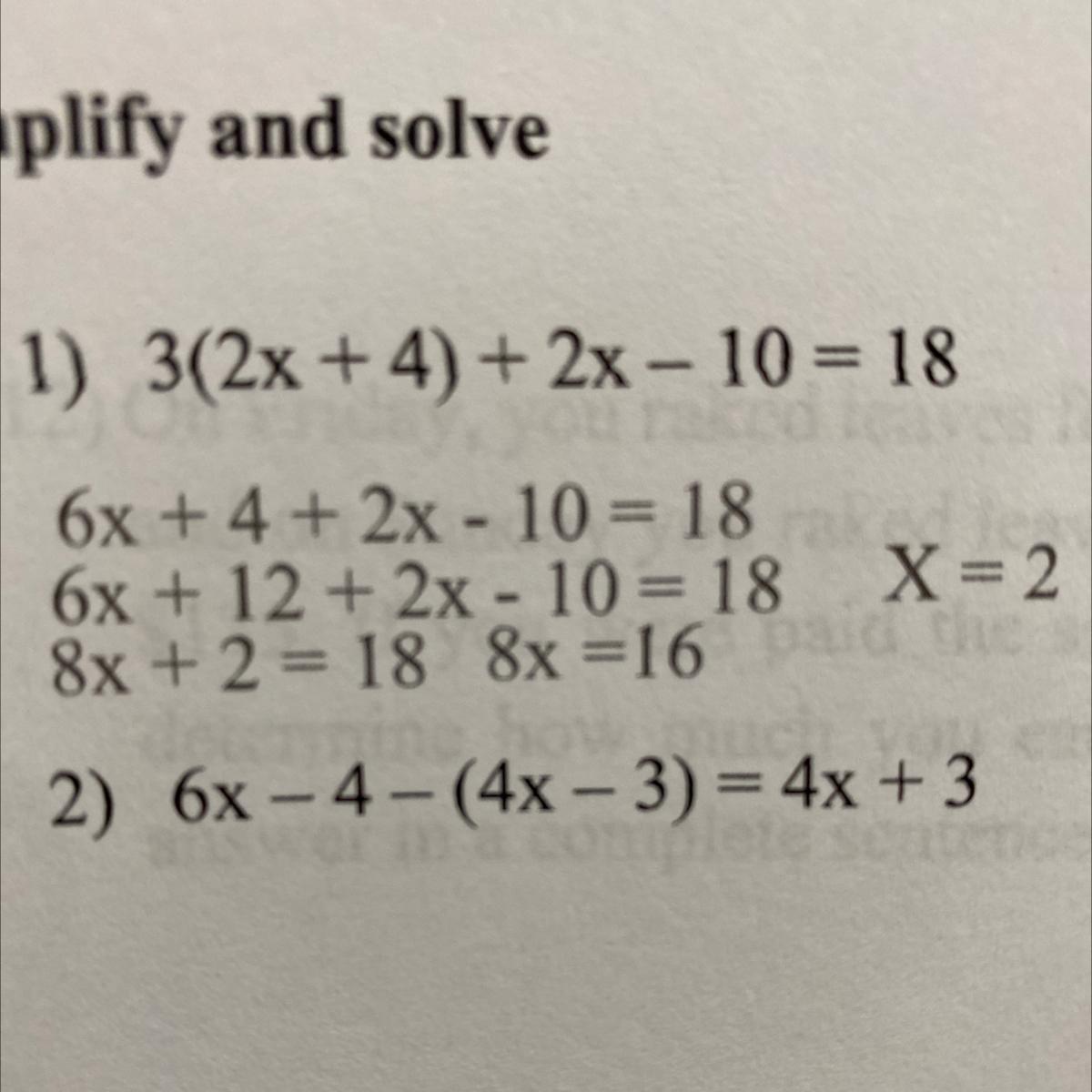
Answers
Given equation is,
\(6x-4-(4x-3)=4x+3\)\(\begin{gathered} 6x-4-4x+3=4x+3 \\ 6x-4x-4+3=4x+3 \\ 2x-1=4x+3 \\ 2z-4x=3+1 \\ -2x=4 \\ x=-\frac{4}{2} \\ x=-2 \end{gathered}\)Thus, x= -2.
On any right triangle, which trigonometric function would you use to determine the opposite side if you knew the angle measure and the length of the hypotenuse?
Sine
Cosine
Tangent
Answers
PLEASE ANSWER ASAP FOR BRAINLEST!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer: Should be 150mm
Step-by-step explanation:
Find the surface area of each figure. Round answers to the nearest tenth, if necessary
2 mm-
2/5 mm
10 mm
3 mm
O
75 mm2
150 mm2
92 mm2
86 mm2
Differentiate the function. f(x) = sin(6 In(x)) Step 1 Recall the Chain Rule in terms of the functions h(x) and g(x), which states that if g is differentiable at x and h is differentiable at g(x), then the composite function F= h og defined by F(x) = (g()) is differentiable at x and F'is given by the following. F'(x) = h'(g(x)).g'(x) We are given the function f(x) = sin(6 In(x)) To write this is the form F(x) = (g(x)) we can let g(x) = 6 In(x) and h(x) =____
Answers
The required differentiation of the function f(x) = sin(6 In(x)) is f'(x) = 6 cos(6 ln(x))/x.
Given the function f(x) = sin(6 In(x)).
To differentiate the function f(x), we need to use the Chain Rule in terms of the functions h(x) and g(x), which states that
if g is differentiable at x and h is differentiable at g(x), then the composite function F= h og defined by F(x) = (g(x)) is
differentiable at x and F' is given by the following.
'(x) = h'(g(x)).g'(x)We can let g(x) = 6 In(x) and h(x) = sin(x).
Now, we can rewrite f(x) as f(x) = h(g(x)) = sin(6 In(x)).
To differentiate this function, we will differentiate h(g(x)) using the Chain Rule.
f'(x) = h'(g(x)) × g'(x)
Substituting the values of h(x) and g(x), we havef'(x) = cos(6 ln(x)) × (6/x) = 6 cos(6 ln(x))/x
Thus, the required differentiation of the function f(x) = sin(6 In(x)) is f'(x) = 6 cos(6 ln(x))/x.
for such more question on function
https://brainly.com/question/25638609
#SPJ11
Select the correct answer.
Each statement describes a transformation of the graph of f(x) = x. Which statement correctly describes the graph of g(x) if g(x) = f(x - 11)?
A. It is the graph of f(x) where the slope is increased by 11.
It is the graph of f(x) translated 11 units to the left.
It is the graph of f(x) translated 11 units up.
It is the graph of f(x) translated 11 units to the right.
B.
C.
OD.
Answers
The correct answer is C. It is the graph of f(x) translated 11 units to the left.
The correct answer is:
C. It is the graph of f(x) translated 11 units to the left.
When we have a function of the form g(x) = f(x - a), it represents a horizontal translation of the graph of f(x) by 'a' units to the right if 'a' is positive and to the left if 'a' is negative.
In this case, g(x) = f(x - 11), which means that the graph of f(x) is being translated 11 units to the right. However, the answer options do not include this specific transformation. The closest option is option C, which states that the graph of g(x) is translated 11 units to the left.
The graph of f(x) = x is a straight line passing through the origin with a slope of 1. If we apply the transformation g(x) = f(x - 11), it means that we are shifting the graph of f(x) 11 units to the right. This results in a new function g(x) that has the same shape and slope as f(x), but is shifted to the right by 11 units.
Therefore, the correct answer is C. It is the graph of f(x) translated 11 units to the left.
for more such question on graph visit
https://brainly.com/question/19040584
#SPJ8
James and Rhea went out for a picnic. James ate 3/8 of a pizza. Rhea ate ¼ of the pizza. What fraction of pizza did they eat altogether?
Answers
Answer:
1/2
Step-by-step explanation:
Find the difference between the sum and product of 2 1/4 and 1 4/5
Answers
Answer: 0 is the answer
if my answer is correct mark as brainliest
Rewrite the fractions as improper fractions:
2 1/4 = 9/4
1 4/5 = 9/5
Rewrite the fractions to have a common denominator:
9/4 = 45/20
9/5 = 36/20
The sum is adding the two together:
45/20 + 36/20 = 81/20
Rewrite as a mixed number:
81/20 = 4 1/20
Product is multiplication:
For multiplying you can use different denominators so you can use the first improper fractions:
9/4 x 9/5 = (9x9)/(4x5) 81/20
Rewrite as a mixed number: 4 1/20
Now subtract to find the difference: 4 1/20 - 4 1/20 = 0
The difference = 0
lily has a garden with a ratio of 6:11 there are 75 more pink flowers than blue flowers. How many pink flowers does she have?
Answers
There are 165 pink flowers in the garden.
What is a ratio?Ratio and Proportion are explained majorly based on fractions. When a fraction is represented in the form of a:b, then it is a ratio whereas a proportion states that two ratios are equal. Here, a and b are any two integers. The ratio and proportion are the two important concepts, and it is the foundation to understand the various concepts in mathematics as well as in science.
Let the number of blue flowers be x, so that number of pink flowers be x + 75
The total flowers will be = 2x + 75
Total share , 6 + 11 = 17
blue's share = 6/17 x (2x + 75)
so that,
6/17 x (2x+75) = x
by cross multiplying
6(2x+75) = 17x
Multiply out
12x + 450 = 17x
collect like terms
17x - 12x = 450
5x = 450
x = 450/5
x = 90
Total pink flowers , x + 75 = 90 + 75
which is 165
In conclusion, the total number of pink flowers would be 165
Learn more about ratio: https://brainly.com/question/2914376
#SPJ1
Suppose that the population size P(t) of the species can be modeled by the following function, where time t is measured in years

Answers
Answer:
378 individuals
601 individuals
Explanation:
We know that the population after t years is described by:
\(P(t)=\frac{790}{1+7e^{-0.31t}}\)So, to know the population after 6 years, we need to replace t by 6 and calculate P(t). Then:
\(\begin{gathered} P(6)=\frac{790}{1+7e^{-0.31(6)}} \\ P(6)=\frac{790}{1+7e^{-1.86}} \\ P(6)=\frac{790}{1+7(0.156)} \\ P(6)=\frac{790}{1+1.089} \\ P(6)=\frac{790}{2.089} \\ P(6)=378 \end{gathered}\)In the same way, we can calculate the population after 10 years replacing t by 10. So:
\(\begin{gathered} P(10)=\frac{790}{1+7e^{-0.31(10)}} \\ P(10)=\frac{790}{1+7e^{-3.1}} \\ P(10)=\frac{790}{1+7(0.045)} \\ P(10)=\frac{790}{1+0.3153} \\ P(10)=\frac{790}{1.3153} \\ P(10)=601 \end{gathered}\)Therefore, the answers are:
378 individuals
601 individuals
A rectangle has a length of 32 yards less than 10 times its width. If the area of the rectangle is 384 square yards, find the length of the rectangle.
Answers
Explanation:
The length of the rectangle is 48 yards.
Let's denote the width of the rectangle as "w" yards.
According to the information given, the length of the rectangle is 32 yards less than 10 times its width. So, the length can be represented as: 10w - 32 yards.
The formula for the area of a rectangle is length times width: Area = length × width.
Given that the area of the rectangle is 384 square yards, we can set up an equation:
Area = length × width
384 = (10w - 32) × w
Now, let's solve for the width (w):
384 = 10w² - 32w
0 = 10w² - 32w - 384
Dividing the equation by 2 to simplify:
0 = 5w² - 16w - 192
Now we have a quadratic equation. We can either factor it or use the quadratic formula to solve for "w." Let's use the quadratic formula:
w = (-b ± √(b² - 4ac)) / 2a
For our equation, a = 5, b = -16, and c = -192. Plugging these values into the formula:
w = (16 ± √((-16)² - 4 × 5 × (-192))) / (2 × 5)
w = (16 ± √(256 + 3840)) / 10
w = (16 ± √4096) / 10
w = (16 ± 64) / 10
This gives us two possible solutions for the width:
w = (16 + 64) / 10 = 8 yards
w = (16 - 64) / 10 = -4.8 yards
Since width can't be negative, we'll ignore the second solution.
So, the width of the rectangle is 8 yards. Now, let's find the length using the earlier expression:
Length = 10w - 32
Length = 10 × 8 - 32
Length = 80 - 32
Length = 48 yards
Therefore, the length of the rectangle is 48 yards.
To know more about length:
https://brainly.com/question/2497593
#SPJ3
What is the intermediate step in the form (x+a)^2=b as a result of completing the square for the following equation?
-5x^2 - 50x = -250
Answers
The required intermediate step is (x-5)² = 25 for the equation -5x² - 50x = -250.
Completing the square is a method used to rewrite the equation in the form (x+a)²=b. The intermediate step involves adding and subtracting the square of half of the coefficient of x in the equation.
To complete the square for the equation -5x² - 50x = -250:
First, we'll add and subtract (1/2 * 50)² = 625/4 on both sides of the equation:
-5x² - 50x + 625/4 = -250 + 625/4
Next, we'll factor out the x term on the left side of the equation:
-5x² - 50x + 625/4 = -250 + 625/4
-5(x² - 10x) + 625/4 = -250 + 625/4
-5(x² - 10x + 25) + 625/4 = -250 + 625/4
-5(x - 5)² + 625/4 = -250 + 625/4
The intermediate step is in the form of (x-5)² = (625/20 + 250)/5
So, the intermediate step is (x-5)² = 25
Learn more about the equation here:
brainly.com/question/13947055
#SPJ1
❗100points❗
y is directly proportional to √x .
y is 24 when x is 36. Find a formula linking x and y
thanks.
Answers
Answer:
y = 4√x
Step-by-step explanation:
Finding the constant of proportionality, k
y = k√x24 = k√36k = 24/6 = 4Equation
y = k√xy = 4√xAnswer:
Y will equal
4√x as the answer
the school lisa goes to is selling tickets to the annual talent show. on the first day of ticket sales the school sold 4 senior citizen tickets and 5 student tickets for a total of $102. the school took in $126 on the second day by selling 7 senior citizen tickets and 5 student tickets. what is the price of on senior citizen ticket and one student ticket?
Answers
Answer: one senior ticket is $8 and one student ticket is $14
Hope this helps a little
Is the triangle with the given side lengths
a right triangle: 1, 2, 5
a. yes
b. no
Answers
Answer:
the answer is yes i took the test
Step-by-step explanation:
In the following image, segment BD bisects segment AC, and three triangles are similar: AABC~ AADB~ ABDC. Complete the two-column
proof of the Pythagorean theorem.
3: A. (AC)DC) + (AC)(CD) = (AC)AC) + (BC)BC)
B. (AC)(CD) + (AC)(AD) = (BC)BC) + (AB)AB)
C. (AB)(CB) + (AD)CD) = (AC)AC) + (BC)BC)
D. (AC)BC) = (AC)(AC) + (BC)BC)
5: A.angle bisector postulate
B. triangles
C. common line segment
D. segment addition postulate

Answers
1. The Fill ups are as follow:
AB² + BC² = AC. AD + AC. CD
2. Segment addition postulate
What is Pythagorean theorem?The relationship between the three sides of a right-angled triangle is explained by the Pythagoras theorem, commonly known as the Pythagorean theorem. The Pythagoras theorem states that the square of a triangle's hypotenuse is equal to the sum of its other two sides' squares.
Given:
BC/ AC = CD/ BC and AB/ AC = AD/ AB
Now, BC² = AC. CD and AB² = AC. AD
Using, Addition Property of Equality
AB² + BC² = AC. AD + AC. CD
and, AB² + BC² = AC (AD + CD) [factor]
AD + CD = AD (segment addition postulate)
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ2
PLATO
i got it correct :)

Please help me with the question; It is attached in the image

Answers
Answer:
The function that passes through (0, 0) is \(f(x) = \frac{1}{6}\cdot e^{2\cdot x^{3}} - \frac{1}{6}\).
Step-by-step explanation:
Firstly, we integrate the function by algebraic substitution:
\(\int {x^{2}\cdot e^{2\cdot x^{3}}} \, dx\) (1)
If \(u = 2\cdot x^{3}\) and \(du = 6\cdot x^{2} dx\), then:
\(\int {e^{2\cdot x^{3}}\cdot x^{2}} \, dx\)
\(\frac{1}{6}\int {e^{u}} \, du\)
\(f(u) = \frac{1}{6}\cdot e^{u} + C\)
\(f(x) = \frac{1}{6}\cdot e^{2\cdot x^{3}} + C\)
Where \(C\) is the integration constant.
If \(x = 0\) and \(f(0) = 0\), then the integration constant is:
\(\frac{1}{6}\cdot e^{2\cdot 0^{3}} + C= 0\)
\(C = -\frac{1}{6}\)
Hence, the function that passes through (0, 0) is \(f(x) = \frac{1}{6}\cdot e^{2\cdot x^{3}} - \frac{1}{6}\).