Find the value of k such that a is singular. (enter your answers as a comma-separated list.) 0 k 1 k 5 k 1 k 0
Answers
The value of k such that a is singular is ±√(5/2).
What do you mean by the term singular?If a singular matrix's determinant is 0, it is a square matrix. Specifically, if and only if det A = 0, a square matrix A is unique. We are aware that the formula A-1 = (adj A) / can be used to get the inverse of a matrix A. Here, the denominator contains det A, which is the determinant of A. We are aware that a fraction with a denominator of 0 is not defined. Since det A = 0, A-1 is not defined. In other words, a single matrix's inverse is not defined. That is to say, there isn't a matrix B such that AB = BA = I.
A singular matrix means that the detA should be 0.
To learn more about singular matrix, Visit:
https://brainly.com/question/11350165
#SPJ4
Related Questions
Someone plz help me :(

Answers
Answer:
i think it is c hope this help's
pic is Step-by-step explanation:

Answer:
quadrant III
Step-by-step explanation:
if 2 ordered pairs are (-x, -y)
that means they are in the quadrant III
the x-coordinate is negative and the y-coordinate is negative in an ordered pair: (−x, −y). For example: (−3, −5)
determine whether the integral is convergent or divergent. if it is convergent, evaluate it. (if the quantity diverges, enter diverges.) 3 34 x4 dx −2
Answers
The integral ∫[-2, 3] x^4 dx is convergent, and its value is 55. It is essential to identify the given integral, determine its convergence or divergence, find the antiderivative of the integrand, apply the Fundamental Theorem of Calculus, and simplify the result. These steps will help us to solve any integrals, and it is important to understand and practice these steps to succeed in calculus.
The given problem is to determine whether the integral ∫[-2, 3] x^4 dx is convergent or divergent and evaluate it if it is convergent. To solve this problem, we need to follow a few steps.
Firstly, we need to identify the given integral, which is a definite integral with lower limit -2 and upper limit 3, and the function is x^4.
Secondly, we need to determine if the integral is convergent or divergent. Since the integrand x^4 is a continuous and well-defined function over the interval [-2, 3], the integral is convergent.
Thirdly, we need to evaluate the convergent integral. To do this, we find the antiderivative of x^4 with respect to x, which is (x^5)/5.
Fourthly, we apply the Fundamental Theorem of Calculus and substitute the limits -2 and 3 into the antiderivative to get [(3^5)/5 - (-2^5)/5] = [243/5 + 32/5] = [275/5].
Finally, we simplify the result, and the final answer is 55. Therefore, the integral ∫[-2, 3] x^4 dx is convergent, and its value is 55.
Learn more about the convergent or divergent integral :
https://brainly.com/question/30726405
#SPJ11
Choose TWO correct answers from the 5 choices.
Need answer ASAP thank you!

Answers
a line passing through the origin which is not contained in any of the three coordinate planes, include and label at least three labeled points on the line
Answers
Three labeled points on the line are (-2, -2m), (0, 0), and (2, 2m), where m is the slope of the line.
A line passing through the origin but not contained in any of the three coordinate planes can be represented by the equation y = mx, where m is the slope of the line. Since the line passes through the origin, the y-intercept is 0.
To find labeled points on the line, we can choose different values for x and calculate the corresponding y-values using the equation y = mx. Let's choose three values for x: -2, 0, and 2.
For x = -2:
y = m(-2) = -2m
So, one labeled point on the line is (-2, -2m).
For x = 0:
y = m(0) = 0
Another labeled point on the line is (0, 0).
For x = 2:
y = m(2) = 2m
So, the third labeled point on the line is (2, 2m).
These three labeled points (-2, -2m), (0, 0), and (2, 2m) lie on the line passing through the origin, and they are not contained in any of the coordinate planes.
Learn more about equation here:
https://brainly.com/question/29657983
#SPJ11
Water is flowing at the rate of 50m^3/min into a holding tank shaped like an cone, sitting vertex down. The tank's base diameter is 40m and a height of 10m.
A.) Write an expression for the rate of change of water level with respect to time, in terms of h ( the waters height in the tank).
B.) Assume that, at t=0, the tank of water is empty. Find the water level, h as a function of the time t.
C.) What is the rate of change of the radius of the cone with respect to time when the water is 8 meters deep?
Answers
A.) The rate of change of the water level with respect to time is (1/4) times the rate of change of the radius with respect to time. B.) The water level h as a function of time t is given by the equation h = 50t. C.) The rate of change of the radius of the cone with respect to time when the water is 8 meters deep is 200.
A.) To find the rate of change of the water level with respect to time, we need to use similar triangles. Let's denote the water level as h (the height of the water in the tank) and let's denote the radius of the water surface as r.
Since the tank is in the shape of a cone, we know that the ratio of the change in radius to the change in height is constant. Therefore, we can write:
(r/40) = (h/10)
To find the rate of change of the water level with respect to time (dh/dt), we differentiate both sides of the equation with respect to time:
(d(r/40)/dt) = (d(h/10)/dt)
Now, let's express the rate of change of the radius with respect to time (dr/dt) in terms of the rate of change of the water level with respect to time:
(dr/dt) = (40/10) * (dh/dt)
Simplifying this expression, we get:
(dr/dt) = 4 * (dh/dt)
Therefore, the rate of change of the water level with respect to time (dh/dt) is (1/4) times the rate of change of the radius with respect to time (dr/dt).
B.) To find the water level h as a function of time t, we need to integrate the rate of change of the water level with respect to time (dh/dt) over time. Since water is flowing into the tank at a constant rate of 50m^3/min, we can write:
dh/dt = 50
Integrating both sides with respect to time, we get:
∫dh = ∫50 dt
h = 50t + C
Since we are given that the tank is initially empty at t = 0, we can substitute h = 0 and t = 0 into the equation:
0 = 50(0) + C
C = 0
Therefore, the equation for the water level h as a function of time t is:
h = 50t
C.) To find the rate of change of the radius of the cone with respect to time when the water is 8 meters deep (h = 8), we can use the relationship we derived earlier:
(dr/dt) = 4 * (dh/dt)
We know that the rate of change of the water level with respect to time is dh/dt = 50. Substituting this into the equation, we get:
(dr/dt) = 4 * 50
(dr/dt) = 200
Therefore, the rate of change of the radius of the cone with respect to time when the water is 8 meters deep is 200.
To know more about rate of change,
https://brainly.com/question/1553593
#SPJ11
La suma de las edades de tres personas es 127años. La mayor tiene 30 años mas que la menor y la del intermedio 26 menos que la menor.¿ calcula la edad de la persona mayor'
Answers
Answer:
La mayor tiene 61 años.
Step-by-step explanation:
Sea x,y,z la edad de la mayor, intermedio y la menor respectivamente.
Tenemos las siguientes ecuaciones:
\(x+y+z=127\) (la suma de las edades es 127)
\(x = z+30\) (la mayor tiene 30 años más que la menor)
La frase "y la del intermedio 26 menos que la menor" no tiene sentido, puesto que esto implicaría que la del intermedio es menor que la menor. Luego se asume que la frase ha de ser "y la del intermedio 26 menos que la mayor"
\(x-26 = y\) (la del intermedio tiene 26 menos que la mayor).
La segunda ecuación se traduce a x-30 =z. Si reemplazamos todo en la primera ecuación obtenemos
\(x+(x-26)+(x-30) = 127\)
Obtenemos la ecuación
\(3x-56 = 127\)
Sumando 56 a ambos lados y dividiendo por 3, obtenemos
\( x = \frac{127+56}{3} = 61\)
Es decir la mayor tiene 61 años.
identify the outputs if the function rule is 2x - 5 and the inputs are 5,10,15
Answers
Answer:
15
Step-by-step explanation:
that is the answer
Initial Knowledge Check
Suppose Deon places $3000 in an account that pays 11% interest compounded each year.
Assume that no withdrawals are made from the account.
Follow the instructions below. Do not do any rounding.
(a) Find the amount in the account at the end of 1 year.
$
(b) Find the amount in the account at the end of 2 years.
Answers
(a) The amount in the account at the end of 1 year is $3330
(b) The amount in the account at the end of 2 year is $3696.3
Compound interest is interest calculated on the principal and the interest accrued in previous periods. General formula for the number of annual interest on the principal. If the interest is compounded annually, the amounts is given by \(A=P(1+\frac{R}{100} )^t\) where "A" represents the new principal sum or the total amount of money after compounding period , "P" represents the original amount or initial amount , "r" is the annual interest rate , "t" represents the number of years .It is given that Deon deposit $3000 that pays 11% interest compounded each year .
(a) Putting P = $3000, R = 11% , T = 1 year in equation (1) , we get
\(A=3000(1+\frac{11}{100} )^1\\\\A=3000(1+0.11)\\A=3000(1.11)\\A=3330\)
(b) Putting P = $3000, R = 11% , T = 2 year in equation (1) , we get
\(A=3000(1+\frac{11}{100} )^2\\\\A=3000(1+0.11)^2\\A=3000(1.11)^2\\A=3000\times1.23\\A=3696.3\)
Learn more about compound interest here :
https://brainly.com/question/24924853
#SPJ9
Which sentence is Correct and please take your time !!!

Answers
Answer:
b
Step-by-step explanation:
Answer:
The answer is the Last one
Factor the polynomial completely
10³ -25r² - 12r + 30

Answers
(5r^2 - 6)(2r - 5)
EXPLANATION
Factor by grouping
(10r^3 - 25r^2) + (-12r + 30)
Factor a GCF
5r^2 (2r - 5) -6 (2r - 5)
Combine groups
(5r^2 - 6)(2r - 5)
CHECK
Use FOIL
First: 5r^2*2r = 10r^3
Outside: 5r^2*-5 = -25r^2
Inside: -6*2r = -12r
Last: -6*-5 = 30
sammies gym has an area of 144 square feet. what is the length of one side of the pool.
Answers
Formulate an equation that would allow you to calculate the percentage of people who filed their taxes during the week of tax day.
Answers
The percentage of people who filed their taxes during the week of tax day is 10%
I can estimate how many people filed their taxes during the week of April 15th using a percentage of 100 is a/b * 100.
A percentage is a portion of a sum divided into 100 equal parts.
Calculate (Number of persons who submitted their taxes during the week of April 15th / total people who filed their taxes that year) times 100 to get the percentage of people who filed during that week.
Let :
a represents the total number of taxpayers during the week of April 15th.
b represents the total number of taxpayers for that year.
The original equation is reduced to
a/b× 100
As an illustration, 100 individuals submitted their taxes the week of April 15th and
Let's say that year, 1000 persons filed their taxes.
= 100/1000 = 10%
Thus, 10% of Americans submitted their taxes during the week of April 15th, or 100 out of 1,000.
Learn more about percentage here:
brainly.com/question/29306119
#SPJ4
f(n) = n^3– 2n
g(n)= 2n + 2
Find (f •g)(n)
Answers
Answer:
\(\boxed{(f~.~g)(x) = 2n^4 + 2n^3 - 4n^2 -4n}\)
.
Step-by-step explanation:
We know that
\(f(n) = n^3 - 2n\)
\(g(n) = 2n + 2\)
.
So
\((f~.~g)(x) = f(n)~.~g(n)\)
\((f~.~g)(x) = (n^3-2n)(2n + 2)\)
\((f~.~g)(x) = n^3(2n + 2) - 2n(2n + 2)\)
\((f~.~g)(x) = 2n^4 + 2n^3 - 4n^2 -4n\)
Answer:
2jj2j wnqj qkwk abaia aow w wka a9w wjw a8uaaia sks sis s8siwobsisi shkahza a
Step-by-step explanation:
bs ak la ya s dyua youa au ab fusn aigska
An experiment has a single factor with six groups and three values in each group. In determining the among-group variation, determining the total variation, there are 17 degrees of freedom. a. If SSA = 140 and SST = 224, what is SSW? b. What is MSA? c. What is MSW? d. What is the value of FSTAT?
Answers
The answer is SSW = 84.MSA is the Mean Square Error for the analysis of variance test of hypothesis for comparing means.
Given, A single factor with six groups and three values in each group. Degrees of freedom = 17.
a) If SSA = 140 and SST = 224,
SSW = SST - SSA = 224 - 140 = 84
b) MSA = SSA / (k - 1) = 140 / (6 - 1) = 28
c) MSW = SSW / (n - k) = 84 / (3 * 6 - 6) = 4.67
d) FSTAT = MSA / MSW = 28 / 4.67 = 6.00
Therefore, SSW = 84, MSA = 28, MSW = 4.67 and FSTAT = 6.00
First we have to find SSW = SST - SSA = 224 - 140 = 84
This is the value of within-group variation.
Hence the answer is SSW = 84.
MSA is the Mean Square Error for the analysis of variance test of hypothesis for comparing means.
Experiment has single factor with 6 groups with 3 values in each group, hence k = 6.MSA = SSA / (k - 1) = 140 / (6 - 1) = 28.
MSW is Mean Square Error which is the variance of the errors in the model.
MSW = SSW / (n - k) = 84 / (3 * 6 - 6) = 4.67
FSTAT = MSA / MSW = 28 / 4.67 = 6.00
Therefore, SSW = 84, MSA = 28, MSW = 4.67 and FSTAT = 6.00.
To know more about Mean Square Error visit :-
https://brainly.com/question/30404070
#SPJ11
write the sequence of natural numbers which leaves the remainder 3 on didvidng by 10
Answers
The sequence of natural numbers that leaves a remainder of 3 when divided by 10 is:
3, 13, 23, 33, 43, 53, 63, 73, 83, 93, 103, 113, ...
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Can someone help me with this ASAP please I’m being timed ! Tom recorded the number of hours he slept each night. He rounds each time to the nearest 1/4. How many hours he slept the night he slept the least

Answers
The colour of your eyes and your shoe size.
Option B is the correct answer.
Find the general solution of the given system. dx/dt = 4x+ 5y dy/dt = 10x + 9y
(x(t), y(t)) =
Answers
x(t) = \(c_1e^1^4^t+c_2e^-^t\) , y(t) = \(2c_1e^1^4^t-c_2e^-^t\) is the general solution of the sytem of differention eqution dx/dt = 4x+ 5y , dy/dt = 10x + 9y .
given dx/dt = 4x+ 5y and dy/dt = 10x + 9y
X'(t) = \(\left[\begin{array}{ccc}4&5\\10&9\end{array}\right]\) X
where X = \(\left[\begin{array}{ccc}x\\y\\\end{array}\right]\)
so A = \(\left[\begin{array}{ccc}4&5\\10&9\end{array}\right]\)
now we need to find eigen value of the matrix and the corresponding eigen vector.
| A- λI | = 0
so after equation the value to zero
λ = 14 and λ = -1
now for the λ = 14 corresponding eigen vector = \(\left[\begin{array}{ccc}1\\2\\\end{array}\right]\)
for λ = -1 corresponding eigen vector = \(\left[\begin{array}{ccc}1\\-1\\\end{array}\right]\)
So general equation is given by:
X(t) = \(c_1e^1^4^t\) \(\left[\begin{array}{ccc}1\\2\\\end{array}\right]\) + \(c_2e^-^t\) \(\left[\begin{array}{ccc}1\\-1\\\end{array}\right]\)
after solving this
x(t) = \(c_1e^1^4^t+c_2e^-^t\)
y(t) = \(2c_1e^1^4^t-c_2e^-^t\)
To know more about Eigen value click below:
https://brainly.com/question/29565569#
#SPJ4
help!!!! pleaseee/.....

Answers
Answer:
I am not sure sowwy i hope you get it tho!!
Step-by-step explanation:
1_2_3_
I need help I need it ASAP!!

Answers
Answer:
50º
Step-by-step explanation:
A triangles angles = 180º
Angle A = 40º
Angle C = 90º (this is a right triangle)
40º + 90º = 130º
180º - 130 º = 50º
where k is an arbitrary constant. for which value(s) of k does this system have a unique solution? for which value(s) of k does the system have infinitely many solutions? for which value(s) of k is the system inconsistent?
Answers
All solutions to the given problem regarding matrices have been explained and answered below.
We have been given the equations,
x + y - z = 2
x + 2y + z = 3
x + y + (k²-5) z = k
the augmented matrix for the given equations will be,
\(\left[\begin{array}{ccc|c}1&1&-1&2\\1&2&1&3\\1&1&(k^{2}-5)&k\end{array}\right]\)
After applying row operations we get the row-reduced form of the matrix, i.e.
\(\left[\begin{array}{ccc|c}1&0&0&\frac{5+k}{2+k} \\0&1&0&\frac{k}{2+k} \\0&0&1&\frac{1}{2+k}\end{array}\right]\)
For a matrix to be no solutions the rank of the matrix has to be lesser than the rank of the augmented matrix,
If we put k = -2, we get
\(\left[\begin{array}{ccc|c}1&0&-3&0\\0&1&2&0 \\0&0&0&1\end{array}\right]\)
∴ for k = -2, we get no solutions for the equations.
For a matrix to be having infinitely many solutions, the rank of the matrix has to be lesser than the no. of variables,
but for no values of k this condition is satisfied for the given equations,
∴ for no values of k, we get infinitely many solutions for the equations.
And for any other of k, the solutions will be unique.
Learn more about systems of linear equalities from,
https://brainly.com/question/21404414?referrer=searchResults
#SPJ4
Five less than the product of a number and -8 is -77
Answers
Answer:
9
Step-by-step explanation:
-77+5=-72
-72 divided by -8 = 9
If (6 ki)² = 27-36i, the value of k is
Answers
Answer: k = √27-i
Step-by-step explanation:
An airplane takes off 12.5 miles south of a city and flies due north at a constant speed of 170 miles per hour. What is the planes position relative to the city after 45 minutes
Answers
Speed =180*3/4
=45*3
=135
135-12.5
The plane is 122.5 miles north to the city after 45 minutes
Just to make sure...are these correct?
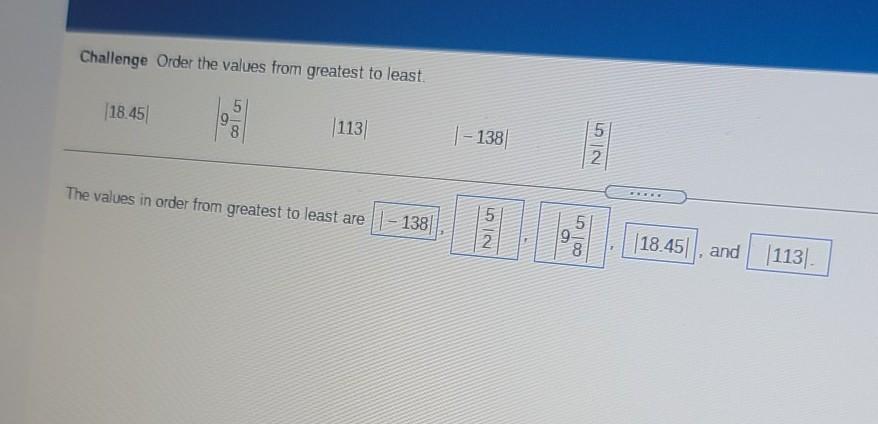
Answers
Answer:
yes
Step-by-step explanation:
yes they are correct
Answer:
No
Step-by-step explanation:
|-138| = 138
|5/2| = |2.5| = 2.5
|9 5/8| = |9.625| = 9.625
|18.45| = 18.45
|113| = 113
Correct order would be:
|-138|, |113|, |18.45|, |9 5/8|, |5/2|
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
write the equation of an ellipse centered at the origin with height 8 units and width 16 units. be sure to show or explain how you got your answer (2 points).
Answers
Answer:
Step-by-step explanation:
The equation of an ellipse centered at the origin with height 8 units and width 16 units is (x² / 64) + (y² / 16) = 1.
To write the equation of an ellipse centered at the origin with height 8 units and width 16 units, we need to determine the semi-major axis (a) and the semi-minor axis (b). The width corresponds to the horizontal axis, and the height corresponds to the vertical axis.
In this case, the width is 16 units, so half of the width, or the semi-major axis, is 8 units. Thus, a = 8. The height is 8 units, so half of the height, or the semi-minor axis, is 4 units. Therefore, b = 4.
Now, we can use the standard equation for an ellipse centered at the origin:
(x² / a²) + (y² / b²) = 1
Plugging in the values of a and b, we get:
(x² / 8²) + (y² / 4²) = 1
(x² / 64) + (y² / 16) = 1
This is the equation of the ellipse centered at the origin with height 8 units and width 16 units.
Learn more about ellipse here: https://brainly.com/question/9702250
#SPJ11
4d+q=14.95. Find d and q.
Answers
Answer:
I love algebra anyways
The ans is in the picture with the steps how i got it
(hope this helps can i plz have brainlist :D hehe)
Step-by-step explanation:


Find the number of possible outcomes for following situation.
Three number cubes are rolled simultaneously.
Answers
Experiment: Rolling three dice simultaneously
No of possible outcomes: 6*6*6 = 216
The Sample space is shown below:
(1,1,1) (1,1,2) (1,1,3) (1,1,4) (1,1,5) (1,1,6)
(1,2,1) (1,2,2) (1,2,3) (1,2,4) (1,2,5) (1,2,6)
(1,3,1) (1,3,2) (1,3,3) (1,3,4) (1,3,5) (1,3,6)
(1,4,1) (1,4,2) (1,4,3) (1,4,4) (1,4,5) (1,4,6)
(1,5,1) (1,5,2) (1,5,3) (1,5,4) (1,5,5) (1,5,6)
(1,6,1) (1,6,2) (1,6,3) (1,6,4) (1,6,5) (1,6,6)
(2,1,1) (2,1,2) (2,1,3) (2,1,4) (2,1,5) (2,1,6)
(2,2,1) (2,2,2) (2,2,3) (2,2,4) (2,2,5) (2,2,6)
(2,3,1) (2,3,2) (2,3,3) (2,3,4) (2,3,5) (2,3,6)
(2,4,1) (2,4,2) (2,4,3) (2,4,4) (2,4,5) (2,4,6)
(2,5,1) (2,5,2) (2,5,3) (2,5,4) (2,5,5) (2,5,6)
(2,6,1) (2,6,2) (2,6,3) (2,6,4) (2,6,5) (2,6,6)
(3,1,1) (3,1,2) (3,1,3) (3,1,4) (3,1,5) (3,1,6)
(3,2,1) (3,2,2) (3,2,3) (3,2,4) (3,2,5) (3,2,6)
(3,3,1) (3,3,2) (3,3,3) (3,3,4) (3,3,5) (3,3,6)
(3,4,1) (3,4,2) (3,4,3) (3,4,4) (3,4,5) (3,4,6)
(3,5,1) (3,5,2) (3,5,3) (3,5,4) (3,5,5) (3,5,6)
(3,6,1) (3,6,2) (3,6,3) (3,6,4) (3,6,5) (3,6,6)
(4,1,1) (4,1,2) (4,1,3) (4,1,4) (4,1,5) (4,1,6)
(4,2,1) (4,2,2) (4,2,3) (4,2,4) (4,2,5) (4,2,6)
(4,3,1) (4,3,2) (4,3,3) (4,3,4) (4,3,5) (4,3,6)
(4,4,1) (4,4,2) (4,4,3) (4,4,4) (4,4,5) (4,4,6)
(4,5,1) (4,5,2) (4,5,3) (4,5,4) (4,5,5) (4,5,6)
(4,6,1) (4,6,2) (4,6,3) (4,6,4) (4,6,5) (4,6,6)
(5,1,1) (5,1,2) (5,1,3) (5,1,4) (5,1,5) (5,1,6)
(5,2,1) (5,2,2) (5,2,3) (5,2,4) (5,2,5) (5,2,6)
(5,3,1) (5,3,2) (5,3,3) (5,3,4) (5,3,5) (5,3,6)
(5,4,1) (5,4,2) (5,4,3) (5,4,4) (5,4,5) (5,4,6)
(5,5,1) (5,5,2) (5,5,3) (5,5,4) (5,5,5) (5,5,6)
(5,6,1) (5,6,2) (5,6,3) (5,6,4) (5,6,5) (5,6,6)
(6,1,1) (6,1,2) (6,1,3) (6,1,4) (6,1,5) (6,1,6)
(6,2,1) (6,2,2) (6,2,3) (6,2,4) (6,2,5) (6,2,6)
(6,3,1) (6,3,2) (6,3,3) (6,3,4) (6,3,5) (6,3,6)
(6,4,1) (6,4,2) (6,4,3) (6,4,4) (6,4,5) (6,4,6)
(6,5,1) (6,5,2) (6,5,3) (6,5,4) (6,5,5) (6,5,6)
(6,6,1) (6,6,2) (6,6,3) (6,6,4) (6,6,5) (6,6,6)
Favorable outcome (three similar numbers, i.e. getting an identical number in all the three dice) : 6
Probability = No of favorable outcomes/Total no of outcomes = 6/216 = 0.0278
In a newspaper, it was reported that yearly robberies in Springfield were up 30% to 260 in 2012 from 2011. How many robberies were there in Springfield in 2011?
Answers
Answer:
182
Step-by-step explanation:
260 x 30% = 78
260 - 78 = 182
Write 2 expressions that canbe used to find the value of x.

Answers
The Solution.
By Trigonometrical Ratios, we have,
SOH, CAH, TOA
Where S
Where in the case at hand,
H = 11
To find the value of x in the given problem,
Taking 25 degrees as our angle of interest, we have,
\(\begin{gathered} \cos 25=\frac{Adj}{Hyp}=\frac{x}{11} \\ \\ \cos 25=\frac{x}{11} \\ \text{Cross multiplying, we get} \\ x=11\cos 25 \end{gathered}\)One of the required expressions is:
\(x=11\cos 25^o\)Similarly, taking 65 degrees as the angle of interest, we have
\(\begin{gathered} \sin 65=\frac{opp}{Hyp}=\frac{x}{11} \\ \\ \sin 65=\frac{x}{11} \\ \text{Cross multiplying, we get} \\ x=11\sin 65 \end{gathered}\)The other required expression for finding x is:
\(x=11\sin 65^o\)The correct answers are;
x = 11 sin 65 degrees
x = 11 cos25 degrees
wo cyclists leave towns kilometers apart at the same time and travel toward each other. one cyclist travels faster than the other. if they meet in hours, what is the rate of each cyclist?
Answers
one cyclist travels faster than the other. Therefore, the rate of the faster cyclist is (distance between towns) / (2 * hours) and the rate of the slower cyclist is also (distance between towns) / (2 * hours).
Let x = the rate of the faster cyclist, and y = the rate of the slower cyclist.
We can set up the equation:
x + y = (distance between towns) / (time they met)
x + y = (distance between towns) / (hours)
We can solve for x and y:
x = (distance between towns) / (2 * hours)
y = (distance between towns) / (2 * hours)
Therefore, the rate of the faster cyclist is (distance between towns) / (2 * hours) and the rate of the slower cyclist is also (distance between towns) / (2 * hours).
Learn more about rate here
https://brainly.com/question/13481529
#SPJ4