Find the value of y when x=2; 4y=5(x-1)
Answers
Subtract what's in the parentheses
4y=5(1)
Multiply 5(1)
4y=5
Divide by 4 to get y by itself
Y=5/4
Answer:
y = 1.25 and/or 1 1/4
Step-by-step explanation:
Substitute 2 for x in the equation.
4y = 5(2-1)
4y = 5(1)
4y = 5
Divide 5 by 4 to isolate the variable.
y = 1.25 and/or 1 1/4
Related Questions
Use a geometric tool to draw a circle. Draw and measure a radius and a diameter of the circle .
Answers
Answer:
Attached is an example of a circle with a radius of 5 and a diameter of 10.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

me pueden dar los resultados?
f(x)=3-x/4
f(x) = √x + 4
f(x) =3x−5/2x+4
f(x) = 4 − x(cuadrado)
f(x) = 1 + √1 + x
Answers
Answer:
The answer is c lma/o
Step-by-step explanation:
Which statement best summarizes the relationship between investments and productivity?
A. Companies with high levels of productivity are the most likely to need investment.
B. Companies must choose between high levels of productivity and large investments. C. Companies use investments to pay for services that improve their productivity.
D. Companies use investments to avoid the need to increase overall productivity.
Answers
The relationship between investments and productivity is that investments can help improve productivity, which is the correct option (C).
What are investments?Investments can be used to acquire new equipment, hire additional workers, or implement new technologies that can enhance a company's productivity.
In general, corporations' major source of revenue is productivity, which is the economic outcome of the company's specific operations, such as the sale of a certain product, the rental of a certain item, the supply of a certain service, and so on.
By investing in these areas, companies can improve their efficiency, reduce costs, and increase output.
Therefore, the relationship between investments and productivity is that investments can help improve productivity.
Learn more about the investments here:
https://brainly.com/question/17619802
#SPJ1
Let f(x) = x ^ 2 + 5 and g(x) = sqrt(x - 5) Find the rules for (fg)(x) (gf)(x)
Answers
Answer:
To find the rules for (fg)(x) and (gf)(x), we need to evaluate the composite functions.
(fg)(x) = f(g(x)) = f(sqrt(x - 5)) = (sqrt(x - 5))^2 + 5 = x - 5 + 5 = x
(gf)(x) = g(f(x)) = g(x^2 + 5) = sqrt(x^2 + 5 - 5) = sqrt(x^2) = |x|
Therefore, the rules for (fg)(x) and (gf)(x) are:
(fg)(x) = x
(gf)(x) = |x|
Step-by-step explanation:
Find the value of the expression
28.6 - 35 + 12.7 - (-5.2)=
Answers
Answer:
Step-by-step explanation:
28.6 - 35 + 12.7 - (-5.2) = ?
28.6 - 35 + 12.7 + 5.2 = 11.5
The value of the expression 28.6 - 35 + 12.7 - (-5.2) is 11.5.
To find the value of the expression, simply follow the order of operations (PEMDAS):
28.6 - 35 + 12.7 - (-5.2)
Step 1: First, deal with the parentheses:
28.6 - 35 + 12.7 + 5.2
Step 2: Then, perform addition and subtraction from left to right:
(28.6 - 35) + 12.7 + 5.2
-6.4 + 12.7 + 5.2
Step 3: Continue with the addition and subtraction:
6.3 + 5.2
Step 4: Finally, calculate the sum:
11.5
To know more about expression:
https://brainly.com/question/32839429
#SPJ2
Ken flips 2 fair coins.
What is the probability of obtaining the same result on each coin?
Answers
Answer:
Hello there! There is a 1/4 chance of getting the same result on both flips, keeping in mind that a coin only has 2 sides.
Step-by-step explanation:
There is a 1/2 chance of getting a result on one flip. So we now have to multiply that by getting the same result on another flip.
1/2 × 1/2 = 1/4
Hope this helps! :)
The probability of obtaining the same result on each coin will be 1/2.
What is probability?Its fundamental concept is that someone will nearly surely occur. The proportion of positive events in comparison to the total of occurrences.
Then the probability is given as,
P = (Favorable event) / (Total event)
Ken flips 2 fair coins. The total events are given as,
Total event = 2 x 2
Total event = 4 {TT, HT, TH, HH}
The probability of obtaining the same result on each coin will be given as,
Favorable events = 2 {TT, HH}
P = 2 / 4
P = 1/2
The probability of obtaining the same result on each coin will be 1/2.
More about the probability link is given below.
https://brainly.com/question/795909
#SPJ2
A quilter created the following shape to use in a block for a new quilt.
A six-sided figure with a large base of 13 inches. The side to the right of the base is 7 and one-half inches. The small side parallel to the base is 5.18 inches. There are two sides that form a point at a right angle. The smaller is 5 inches, and the larger is 6 inches.
What is the area of the shape for the quilt block?
sixty-three and three fourths in2
one hundred twelve and one half in2
one hundred twenty-seven and one half in2
225 in2
Answers
The total area of the quilt is: 112.5 square inches
How to determine the total area of the quilt?The six-sided figure is given, and we can deduce the following parameters from the question:
The shape is made of a triangle and a rectangle
The side lengths derived from the question are:
The triangle on top:
base: 5 inches and height: 5.18 inches
The rectangle at the bottom:
Base: 16 inches with a height of 7.5 inches
So, we have the total area of the figure to be
Area of figure = 1/2 * 5 * 6 + 13 * 7.5
Area of figure = 112.5
Based on the parameters, the total area is 112.5 square inches
Read more about Area at: https://brainly.com/question/15351887
#SPJ1
The bones were about ___ years old. Round to the nearest integer as needed.

Answers
Since they lost 69.1 %, only 30.9 % remains. The correct equation for the remaining amount is
\(A(t)=A_0(0.5)^{\frac{t}{5750}}\)t = years since 100% was present, A0 = initial amount = 100% .
Get time T to drop to 30.9% from
\(30.9=100(0.5)^{\frac{T}{5750}}\)\(0.309=(0.5)^{\frac{T}{5750}}\)Take log both sides,
\(\log 0.309=\frac{T}{5750}\log 0.5\)\(-0.51004=\frac{T}{5750}(-0.30103)\)\(1.694=\frac{T}{5750}\)\(T=9742.3\text{ years}\)Hence the bones are 9742.3 years old when they are discovered.
100 Points, please provide full explanation.

Answers
The term "100 points" usually indicates a high level of achievement or success in a particular area.
The term "100 points" can refer to a number of different things depending on the context. For example, in sports, it could refer to a team scoring 100 points in a game.
In wine tasting, it could refer to a perfect score given to a wine by a critic or judge. In school, it could refer to receiving a perfect score on an exam or assignment worth 100 points.
It's important to note that while a perfect score of 100 points is often seen as the ultimate goal, it's not always necessary or even possible in some situations. In many cases, simply doing your best and striving for improvement is enough to be considered successful.
To learn more about : points
https://brainly.com/question/23848540
#SPJ8
The question is attached below

Answers
The expected number of pizzas to be stuffed crust is given as follows:
500.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
The sample size is given as follows:
408 + 224 + 208 + 200 = 1040.
Out of these, 208 are stuffed crust, hence the probability is given as follows:
p = 208/1040.
Out of 2500 pizzas, the expected number is then given as follows:
E(X) = 2500 x 208/1040
E(X) = 500.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
Please answer this before friday
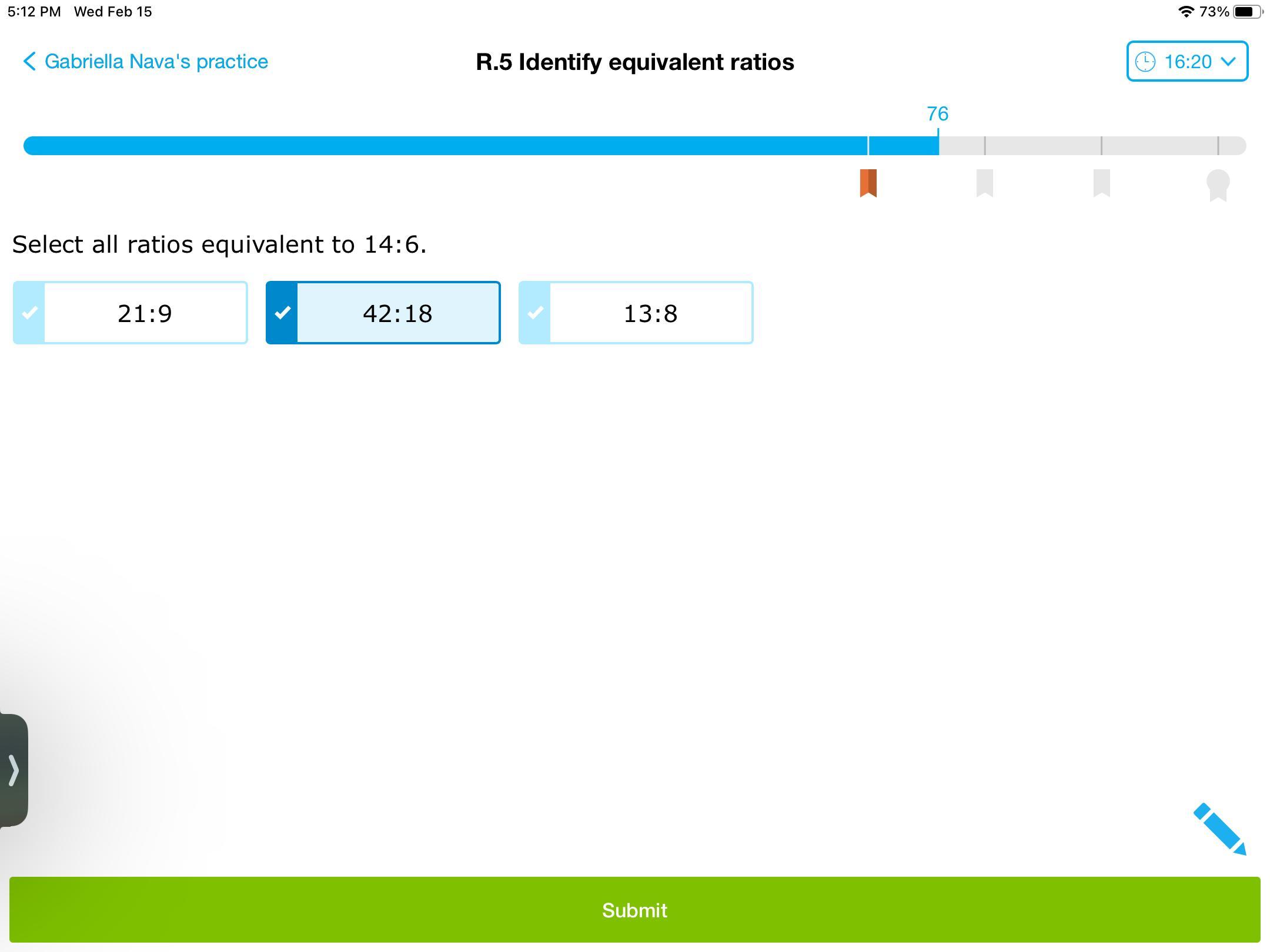
Answers
Answer: 21:9 and 42:18
Step-by-step explanation:
14:6 at its most basic form is 7:3, so find anything that could be equal to this if a number is multiplied on both sides.
21:9 is our simplified ratio multiplied by 3 on both sides.
42:18 is our simplified ratio multiplied by 6 on both sides.
But, the final ratio doesn't work, because 7 and 3 respectively cannot multiply to 13 and 8 with the same value.
00:00
Gavin counted the number of days until the end of school.
If he counted the days in groups of 7, which list shows the numbers Gavin could have
named?
O
A. 7, 15, 22, 30
B. 7, 14, 21, 30
O
C. 7, 14, 21, 28
D. 14, 21, 32, 38
Answers
Answer:
C. 7, 14, 21, 28
Step-by-step explanation:
We want to find the multiples of 7
7*1= 7
7*2 = 14
7*3= 21
7*4 = 28
Answer:
The answer is, C. 7, 14, 21, 28
A straw is placed inside a rectangular box that is 2 inches by 5 inches by 9 inches, as shown. If the straw fits exactly into the box diagonally from the bottom left corner to the top right back corner, how long is the straw? Leave your answer in simplest radical form.
Answers
The length of the straw is √110 inches.
What is rectangle ?
Rectangle can be defined as opposites sides are equal and the area of rectangle is product of length and breadth.
We can use the Pythagorean theorem to find the length of the diagonal of the rectangular box, which will be the length of the straw.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
In this case, the rectangular box forms a right triangle, and the length of the hypotenuse is the length of the diagonal from the bottom left corner to the top right back corner, which is the length of the straw.
The lengths of the other two sides of the triangle are the dimensions of the rectangular box:
The width is 2 inches, which is the length of one leg of the right triangle.
The height is 5 inches, which is the length of the other leg of the right triangle.
So we can use the Pythagorean theorem as follows:
length of straw = √(2*2 + 5*5 + 9*9)
= √(4 + 25 + 81)
= √110
Therefore, the length of the straw is √110 inches.
To learn more about Rectangle from given link.
https://brainly.com/question/29123947
#SPJ1
A rectangular box is designed to have a square base and an open top. The volume is to be 500in.3 What is the minimum surface area that such a box can have?
Answers
The minimum surface area that such a box can have is 380 square
How to determine the minimum surface area such a box can have?Represent the base length with x and the bwith h.
So, the volume is
V = x^2h
This gives
x^2h = 500
Make h the subject
h = 500/x^2
The surface area is
S = 2(x^2 + 2xh)
Expand
S = 2x^2 + 4xh
Substitute h = 500/x^2
S = 2x^2 + 4x * 500/x^2
Evaluate
S = 2x^2 + 2000/x
Differentiate
S' = 4x - 2000/x^2
Set the equation to 0
4x - 2000/x^2 = 0
Multiply through by x^2
4x^3 - 2000 = 0
This gives
4x^3= 2000
Divide by 4
x^3 = 500
Take the cube root
x = 7.94
Substitute x = 7.94 in S = 2x^2 + 2000/x
S = 2 * 7.94^2 + 2000/7.94
Evaluate
S = 380
Hence, the minimum surface area that such a box can have is 380 square
Read more about surface area at
https://brainly.com/question/76387
#SPJ1
Help me solve these two problems! Show the work

Answers
Answer:
see explanation
Step-by-step explanation:
2
4x² + 64 ← factor out the common factor of 4 from each term
= 4(x² + 16)
3
(a - 10)² = 121 ( take square root of both sides )
a - 10 = ± \(\sqrt{121}\) = ± 11 ( add 10 to both sides )
a = 10 ± 11
then
a = 10 - 11 = - 1
a = 10 + 11 = 21
can someone please help me find the answer to the following?

Answers
Answer:
1077.19 ft
Explanation:
Using the depression angle, we get that one of the angles of the formed triangle is also 18° because they are alternate interior angles, so we get:
Now, we can relate the distance x, the angle of 18°, and the height of the tower using the trigonometric function tangent, so:
\(\begin{gathered} \tan 18=\frac{Opposite}{Adjacent} \\ \tan 18=\frac{350}{x} \end{gathered}\)Now, solving for x, we get:
\(\begin{gathered} x\cdot\tan 18=x\cdot\frac{350}{x} \\ x\cdot\tan 18=350 \\ \frac{x\cdot\tan18}{\tan18}=\frac{350}{\tan 18} \\ x=\frac{350}{\tan 18} \end{gathered}\)Using the calculator, we get that tan(18) = 0.325, so x is equal to:
\(x=\frac{350}{0.325}=1077.19\text{ }ft\)Therefore, the forest ranger is at 1077.19 ft from the fire.

PLEASE HELP ME
The function f(x) = -2(4)^x+1 +140
represents the number of tokens a child has x hours after arriving at an arcade.
What is the practical domain and range of the function?
If necessary, round to the nearest hundredth.
The practical domain of the situation is ?
The practical range of the situation is ?
PLEASE SEE PHOTO FOR FUNCTION

Answers
The function f(x) = -2(4)ˣ⁺¹ +140 represents the number of tokens a child has x hours after arriving at an arcade. The practical domain and range of the function are x ≥ 0 and The practical range of the situation is [140, ∞).
The given function is f(x) = -2(4)ˣ⁺¹+ 140, which represents the number of tokens a child has x hours after arriving at an arcade.
To determine the practical domain and range of the function, we need to consider the constraints and limitations of the situation.
For the practical domain, we need to identify the valid values for x, which in this case represents the number of hours the child has been at the arcade. Since time cannot be negative in this context, the practical domain is x ≥ 0, meaning x is a non-negative number or zero.
Therefore, the practical domain of the situation is x ≥ 0.
For the practical range, we need to determine the possible values for the number of tokens the child can have. Looking at the given function, we can see that the term -2(4)ˣ⁺¹represents a decreasing exponential function as x increases. The constant term +140 is added to shift the graph upward.
Since the exponential term decreases as x increases, the function will have a maximum value at x = 0 and approach negative infinity as x approaches infinity. However, due to the presence of the +140 term, the actual range will be shifted upward by 140 units.
Therefore, the practical range of the situation will be all real numbers greater than or equal to 140. In interval notation, we can express it as [140, ∞).
To summarize:
- The practical domain of the situation is x ≥ 0.
- The practical range of the situation is [140, ∞).
Know more about the domain here:
https://brainly.com/question/30096754
#SPJ8
Mr. Marlon buys these tickets for his family to visit the water park. The total cost is $210. Write and solve an equation to find the cost of each ticket.
Answers
Answer:
$52.50
Step-by-step explanation:
210 divided by 4 equals 52.50
Hello all! Please help me out with this.
I want to find a certain number which I will call Y. It is four times as great as another number which is two less than twenty. What is Y?
Answers
Answer:
Y=72
Step-by-step explanation:
First we set up the equation which is (20-2) times 4=Y
Then we solve, 20 minus 2 is risk since it is in the parentheses. 20 minus 2 is 18.
After that 18 times 4 is 72
Y=72
Sa piajes egne baseball games this season. Her point totais for each game were 8. 14.4 7.6.14, 4 and 7. What was
the mean number of points she scoret per game?
Answers
Answer:
The mean number of scores per game is 8
Step-by-step explanation:
Since we know we can find the mean by adding all the numbers and dividing them by many numbers there were. Once you add 8, 14, 4, 7, 6, 4, and 7, you will get 64. Since there were 8 numbers, you divide 64 by 8 to get 8.
i need help with this problem

Answers
Answer:
[g+2/3g-1] ÷ [g^2+2g/6g+2]
g+2/3g-1 × 6g+2/g^2+2g
g+2/3g-1 × 2(3g +1)/g(g+2)
1/ 3g-1 × 2(3g+1)/g
2(3g +1)÷ g(3g-1)
6g+2 ÷[3g^2-g]
what is the y- intercept of a line that has a slope of -3 and passes through point (-5,4)?
Answers
Answer:B is the answer -11
Step-by-step explanation:
Find the rate of change demonstrated in the graph below.
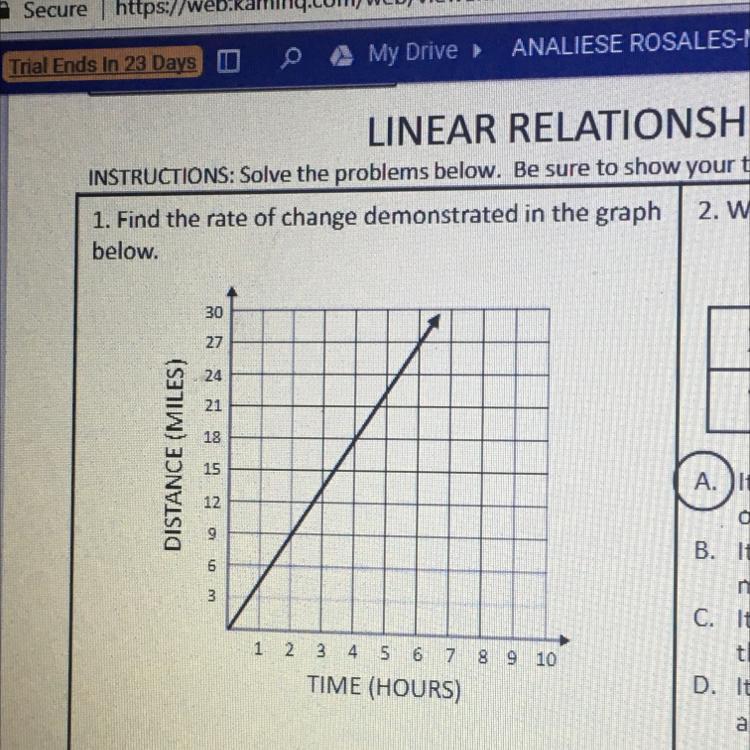
Answers
Answer:
Rate of change = \( \frac{9}{2} = 4.5 \).
Step-by-step explanation:
Rate of change = \( \frac{y_2 - y_1}{x_2 - x_1} \).
Use the coordinates of two points on the graph. (Any point can be chosen. We will still arrive at the same rate of change).
Using (2, 9) and (4, 18),
Let,
\( (2, 9) = (x_1, y_1) \)
\( (4, 18) = (x_2, y_2) \)
Rate of change = \( \frac{18 - 9}{4 - 2} = \frac{9}{2} = 4.5 \).
Jan raised $120.75 at the car wash. If each wash costs $5.75, how many cars did she wash?
Answers
Answer:
She washed 21 cars
Step-by-step explanation:
Answer:
Jan washed 21 cars
Step-by-step explanation:
120.75 / (Divided) 5.75=21
If you were to times 5.75 by 21 you will get the amount she rasied at the car wash
100 Points! Algebra question. Solve the equation. Please show as much work as possible. Photo attached. Thank you!

Answers
2^-3x+18 = 2^27x-6
move the terms
-3x+18=27x-6
collect like terms
-3x-27x=-6-18
divide both sides
-30x=-24
answer : x=4/5
-2a-6a-9=-9-6a-2a
help please g
Answers
Answer:
the solution to the equation -2a - 6a - 9 = -9 - 6a - 2a is all real numbers, or (-∞, +∞).
Step-by-step explanation:
To solve this equation for "a", you need to simplify and rearrange the terms so that all the "a" terms are on one side of the equation and all the constant terms are on the other side. Here are the steps:
Start by combining the "a" terms on the left side of the equation: -2a - 6a = -8a. The equation now becomes: -8a - 9 = -9 - 6a - 2a.
Combine the constant terms on the right side of the equation: -9 - 2a - 6a = -9 - 8a. The equation now becomes: -8a - 9 = -9 - 8a.
Notice that the "a" terms cancel out on both sides of the equation. This means that the equation is true for any value of "a". Therefore, the solution is all real numbers, or in interval notation: (-∞, +∞).
In summary, the solution to the equation -2a - 6a - 9 = -9 - 6a - 2a is all real numbers, or (-∞, +∞).
-8x+14 = -15x+10
x = ?
Answers
Answer:
-4/7
Step-by-step explanation:
Add 15x to each side. Then subtract 14 to each side.
Caroline surveyed 380 of the students in her school about their favorite color. 209 students said their favorite color was blue. What percentage of the surveyed students said their favorite color was blue?
Answers
Answer:
55% of the students surveyed said their favorite color was blue
Step-by-step explanation:
\(\frac{209}{380}\) as a percent = 55%, or 0.55 in decimal form.
For the given equation, find the values of a, b, and c, determine the direction in which the parabola opens, and determine the y-intercept. Decide which table best illustrates these values for the equation:
y = 3 x squared + 2 x minus 8

Answers
Answer:
Table A
Step-by-step explanation:
y = 3x^2 +2x -8
The quadratic is in the form
y = a x^2 +bx+c
a = 3 b = 2 c = -8
Since a > 0 it opens up
The y intercept is c so the y intercept is -8
cot(sin-1) square rootx2
Answers
The algebric expression \(cot(sin^{(-1)}\sqrt{(x^2}\)simplifies to sqrt(1 - |x|^2) / |x|.
The expression "cot(sin^(-1)(sqrt(x^2)))" involves trigonometric and square root functions. Let's break it down step by step to simplify the expression.
Inside the square root: x^2.
The square root of x^2 is |x| (the absolute value of x), as the square root eliminates the square and keeps the positive value.
The expression sin^(-1)(sqrt(x^2)) is equivalent to arcsin(sqrt(x^2)).
Since we already know that the square root of x^2 is |x|, we can rewrite the expression as arcsin(|x|).
Now, we have cot(arcsin(|x|)).
The cotangent (cot) of an angle is equal to the reciprocal of the tangent (tan) of the same angle.
So, cot(arcsin(|x|)) can be written as 1 / tan(arcsin(|x|)).
Using the inverse trigonometric identity, tan(arcsin(x)) = x / sqrt(1 - x^2), we can simplify further.
In our case, x = |x|.
Therefore, tan(arcsin(|x|)) = |x| / sqrt(1 - |x|^2).
Substituting this result back into the expression, we have 1 / (|x| / sqrt(1 - |x|^2)).
To divide by a fraction, we multiply by its reciprocal.
Hence, the final simplification of the expression is sqrt(1 - |x|^2) / |x|.
For more such question on algebric expression visit:
https://brainly.com/question/4344214
#SPJ8