Answers
Answer: \(1460.96ft^3\)
Step-by-step explanation:
You have a cylinder and a cuboid. Find each of these figures' volume individually and add them together.
Cylinder:
height = 4ft
radius = 4ft
\(Formula: V=\pi r^2h\)
\(V=(3.14)(4ft)^2(4ft)\\V=(3.14)(16ft^2)(4ft)\\V=(3.14)(64ft^3)\\V=200.96ft^3\)
---------------------------------------------------------------------------------------------------
Cuboid:
\(Formula: V = l*w*h\)
\(V=(15ft)(7ft)(12ft)\\V=1260ft^3\)
------------------------------------------------------------------------------------------------------
Add these two volumes together.
\(200.96ft^3+1260ft^3=1460.96ft^3\)
Related Questions
minimize f(x) = |x+3| + x^3 S.t. x sum [-2, 6]
Answers
Minimization of f(x) = |x+3| + x^3 at the endpoints (-2 and 6) the minimum value of the function is approximately 3.84, which occurs at x= \sqrt{1/3}
within the given interval.
To minimize the function subject to the constraint f(x) = |x+3| + x^3 that x lies in the interval [-2, 6], we need to find the value of x that minimizes f(x) within that interval.
First, let's analyze the function f(x). The absolute value term |x+3| can be rewritten as:
|x+3| =
x+3 if x+3 >= 0
-(x+3) if x+3 < 0
Since the interval [-2, 6] includes both positive and negative values of x+3, we need to consider both cases.
Case 1: x+3 >= 0
In this case, f(x) = (x+3) + x^3 = 2x + x^3 + 3
Case 2: x+3 < 0
In this case, f(x) = -(x+3) + x^3 = -2x + x^3 - 3
Now, we can find the minimum of f(x) within the given interval by evaluating the function at the endpoints (-2 and 6) and at any critical points within the interval.
Calculating the values of f(x) at x = -2, 6, and the critical points, we can determine the minimum value of f(x) and the corresponding value of x.
Since the equation involves both absolute value and a cubic term, it is not possible to find a closed-form solution or an exact minimum value without numerical methods or approximation techniques.
For more such questions on function
https://brainly.com/question/29631554
#SPJ8
What's u? For this equation

Answers
Answer:
Step-by-step explanation:
2u - 1 = 3
In this equation, you would first take 3 + 1 to get 4. You know that 2 x 2 = 4 so u = 2.
Hello! I am confused with my practice worksheet the equation is -5+25x-40x-10=-4x-8x
Answers
Answer:
Combine like terms on the left side of equation first
then solve the equation normally
Step-by-step explanation:
What is the answer for 7.56 ÷ 2.4 − 0.65
Answers
Answer:
2.5
Step-by-step explanation:
To subtract fractions, find the LCD and then combine it.
y=−2x+2
4x+2y=4
Substitute the resulting expression in the other equation
Answers
Answer:
In this section we will discuss the method of graphing an equation in two variables. In other words, we will sketch a picture of an equation in two variables.
Step-by-step explanation:
Review the graph of the function f(x).
On a coordinate plane, a curve starts at closed circle (1, negative 2) and curves up through (0, 1) to (negative 5, 2).
The function shown has an endpoint discontinuity. Which statement describes the one-sided limits at the discontinuity?

Answers
Answer:
b
Step-by-step explanation:
edg 2020
'Function' is described as 'a relation in which each component of the domain is related to precisely one component of the codomain.'
B). The statement second "Limit of f(x) = - 2 as x approaches 1 minus. Limit of f(x) DNE as x approaches 1+" correctly elaborates the single-sided limits when the end-point dislocates.
'End-point discontinuity' is described as a function that carries a shut endpoint at its interlude.While 'one-sided limits' are described as the limit(any out of the two) belonging to a function (x) when x advances towards either side(left or right). Thus, it limits x and the rest values remain the same. In the given function, the one-sided limit of the function(x) equals to -2 when it advances towards -1 and DNE when it advances towards 1+.Thus, option B is the correct answer.
Learn more about 'function' here:
brainly.com/question/23505310

Luke randomly selects 25 students from his school and asks each of them how many minutes they read each night to find out how much, on average, students at his school read. This represents which type of data collection?
A: Census
B: Experiment
C: Observation
D: Sample
Answers
I'm pretty sure it's census
Domain and Range, Help!!!

Answers
Answer:
Increasing
Domain: [-5, ∞)
Domain: x≥-5
Range: [-0.5,∞)
Range: y≥-0.5
Emeline has a shoe box measuring 11 x6x8. Noah has one measuring 12 x 5 x 7. What is the difference is surface area
between their boxes?
Answers
Answer: 46
Step-by-step explanation:

NEED HELP ASAP. I don not understand why I'm wrong. What is the right answer???

Answers
Answer:
Answer: 35/18
Step-by-step explanation:
\( \frac{ \{ \frac{3}{4} - \frac{5}{2} \} }{ \{ \frac{3}{5} - \frac{3}{2} \}} = \frac{( - \frac{7}{4} )}{ (- \frac{9}{10} )} \\ \\ = \frac{7}{4} \div \frac{9}{10} \)
use the reciprocal of 9/10 :
\( = \frac{7}{4} \times \frac{10}{9} \\ \\ = \frac{35}{18} \)
\( \huge \boxed{\mathfrak{Question} \downarrow}\)
Simplify \(\huge \sf\frac { \frac { 3 } { 4 } - \frac { 5 } { 2 } } { \frac { 3 } { 5 } - \frac { 3 } { 2 } } \\ \)\( \large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}\)
\( \huge \sf\frac { \frac { 3 } { 4 } - \frac { 5 } { 2 } } { \frac { 3 } { 5 } - \frac { 3 } { 2 } } \\ \)
The least common multiple of 4 and 2 is 4. Convert \(\sf\frac{3}{4} \)and \(\sf\frac{5}{2} \)to fractions with denominator 4.\( \huge \sf \frac{\frac{3}{4}-\frac{10}{4}}{\frac{3}{5}-\frac{3}{2}} \\ \)
Because \(\sf\frac{3}{4} \)and \(\sf \frac{10}{4}\) have the same denominator, subtract them by subtracting their numerators.\( \huge \sf\frac{\frac{3-10}{4}}{\frac{3}{5}-\frac{3}{2}} \\ \)
Subtract 10 from 3 to get -7.\( \huge \sf\frac{-\frac{7}{4}}{\frac{3}{5}-\frac{3}{2}} \\ \)
The least common multiple of 5 and 2 is 10. Convert \(\sf\frac{3}{5}\) and \(\sf \frac{3}{2}\) to fractions with denominator 10.\( \huge \sf\frac{-\frac{7}{4}}{\frac{6}{10}-\frac{15}{10}} \\ \)
Because \(\sf \frac{6}{10}\) and \(\sf \frac{15}{10}\) have the same denominator, subtract them by subtracting their numerators.\( \huge \sf\frac{-\frac{7}{4}}{\frac{6-15}{10}} \\ \)
Subtract 15 from 6 to get -9.\( \huge \sf\frac{-\frac{7}{4}}{-\frac{9}{10}} \\ \)
Divide \(\sf-\frac{7}{4}\) by \(\sf-\frac{9}{10}\) by multiplying \(\sf-\frac{7}{4}\) by the reciprocal of \(\sf-\frac{9}{10}\).\( \huge \sf-\frac{7}{4}\left(-\frac{10}{9}\right) \)
Multiply \(\sf-\frac{7}{4}\) by \(\sf-\frac{10}{9}\) by multiplying the numerator by the numerator and the denominator by the denominator.\( \huge \sf\frac{-7\left(-10\right)}{4\times 9} \)
Carry out the multiplications in the fraction \(\sf\frac{-7\left(-10\right)}{4\times 9}\).\( \huge \sf\frac{70}{36} \)
Reduce the fraction \(\sf\frac{70}{36}\) to its lowest terms by extracting and cancelling out 2.\( \huge \boxed{ \bf\frac{35}{18}\approx 1.944..}\)
What is the solution of the equation? √2x – 5+ 4 = x
Answers
Answer:
2x−1
Step-by-step explanation:
what degrees do you need to rotate a fan?

Answers
Answer:
360°
Step-by-step explanation:
degrees are needed
how much do i need to make to afford a $425,000 house
Answers
The income you need to afford a $425,000 house is largely dependent on your debt-to-income ratio, credit score, and down payment. However, a general rule of thumb is to have an annual income that is at least three times the purchase price of the home, which in this case would be $1,275,000.
To more accurately determine the income needed to afford a $425,000 house, consider factors such as the interest rate on the mortgage, property taxes, homeowners insurance, and any homeowner association fees.
These additional expenses can significantly impact your monthly mortgage payment and thus your income requirements.
It's important to keep in mind that lenders have varying criteria when determining mortgage eligibility and income requirements, so it's best to speak with a mortgage professional to get a more accurate estimate based on your individual circumstances.
for such more questions on income
https://brainly.com/question/28414951
#SPJ8
George is saving his money. He started with $125.00. If he adds $75.00 to his savings each month, how
much will he have saved after 6 months
Answers
Answer:
$575.00
Step-by-step explanation:
75 * 6=450
450+125=575
Un paese contava 12000 abitanti all'inizio del 2007 durante l'anno i nati sono 1,7 % del totale degli abitanti e morti sono 2% calcola Quanti sono i nati e quanti sono i morti nel 2007 Calcola inoltre Qual è la popolazione all'inizio del 2008
Answers
Step-by-step explanation:
12000 abitanti all'inizio del 2007
nati: 1.7% × 12000 = 204
morti: 2% × 12000 = 240
popolazione all'inizio del 2008: 12000 + 204 - 240 = 11964
Select all equations that are true

Answers
UNIT RATE TRUE OR FALSE HELP ME!!!

Answers
Answer:
False
Step-by-step explanation:
This is not a unit rate because neither of the rates are equal to 1. A unit rate, for example, could be 25 ft per second.
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather
can someone help me answer this

Answers
\(32^{-\tfrac 25}\\\\=(2^5)^{-\tfrac 25}\\\\=2^{-2}\\\\=\dfrac 1{2^2}\\\\=\dfrac 14\)

Consider these three numbers expressed in scientific notation: 8.2 × 10-3, 5.2 × 10-6, and 4.1 × 10-6. Which number is the greatest, and by how many times is it greater than the smallest number?
Answers
Answer: 8.2×10-3^1, I think the second part of the answer is 4.4×10^1 (44)
I think this is right but I'm not a mathematician.
Step-by-step explanation:
The first problem is 7.9×10^1 (79)
Second problem 4.6×10^1 (46)
Third problem 3.5×10^1 (35)
what property is used to get from step 1 : 5x-2=0 to step 2 : 5x=2
Answers
Answer:
Addition Property of Equality.
Step-by-step explanation:
The Addition property of equality states that: "If two expressions are equal to each other, and you add the same value to both sides of the equation, the equation will remain equal" (http://content.nroc.org).
For example:
x = x is the same as x + 1 = x + 1
the one is the added same value "to both sides of the equation".
Solving in extremely detailed steps:
(you only take one step normally, from 5x-2=0 to 5x=2, but because we are explaining the concept of the property, we will use lots detailed of steps)
5x - 2 = 0
5x - 2 + 2 = 0 + 2
5x + 0 = 2
5x = 2
and r(x) = 3x² If P(x)=x²-3x²-1/2 x + 10, Q(x) = ²x² - 1x ²-1/2 X- subtract R(x) from the sum of P(x) and Q(x). 6x + 1 then find p(x) + q(x) - r(x). 3 5 and R(x) - 34 X + the 4X
Answers
Answer:Z
cos x dx = sin x + C
Z
sec2 x dx = tan x + C
Z
sec x tan x dx = sec x + C
Z
1
1 + x2
dx = arctan x + C
Z
1
√
1 − x2
dx = arcsin x + C
8.1 Substitution
Needless to say, most problems we encounter will not be so simple. Here’s a slightly more
complicated example: find
Z
2x cos(x
2
) dx.
This is not a “simple” derivative, but a little thought reveals that it must have come from
an application of the chain rule. Multiplied on the “outside” is 2x, which is the derivative
of the “inside” function x
2
. Checking:
d
dx sin(x
2
) = cos(x
2
)
d
dxx
2 = 2x cos(x
2
),
so Z
2x cos(x
2
) dx = sin(x
2
) + C.
Even when the chain rule has “produced” a certain derivative, it is not always easy to
see. Consider this problem:
Z
x
3
p
1 − x
2 dx.
There are two factors in this expression, x
3
and p
1 − x
2, but it is not apparent that the
chain rule is involved. Some clever rearrangement reveals that it is:
Z
x
3
p
1 − x
2 dx =
Z
(−2x)
−
1
2
(1 − (1 − x
2
))p
1 − x
2 dx.
This looks messy, but we do now have something that looks like the result of the chain
rule: the function 1 − x
2 has been substituted into −(1/2)(1 − x)
√
x, and the derivative
Step-by-step explanation:Z
cos x dx = sin x + C
Z
sec2 x dx = tan x + C
Z
sec x tan x dx = sec x + C
Z
1
1 + x2
dx = arctan x + C
Z
1
√
1 − x2
dx = arcsin x + C
8.1 Substitution
Needless to say, most problems we encounter will not be so simple. Here’s a slightly more
complicated example: find
Z
2x cos(x
2
) dx.
This is not a “simple” derivative, but a little thought reveals that it must have come from
an application of the chain rule. Multiplied on the “outside” is 2x, which is the derivative
of the “inside” function x
2
. Checking:
d
dx sin(x
2
) = cos(x
2
)
d
dxx
2 = 2x cos(x
2
),
so Z
2x cos(x
2
) dx = sin(x
2
) + C.
Even when the chain rule has “produced” a certain derivative, it is not always easy to
see. Consider this problem:
Z
x
3
p
1 − x
2 dx.
There are two factors in this expression, x
3
and p
1 − x
2, but it is not apparent that the
chain rule is involved. Some clever rearrangement reveals that it is:
Z
x
3
p
1 − x
2 dx =
Z
(−2x)
−
1
2
(1 − (1 − x
2
))p
1 − x
2 dx.
This looks messy, but we do now have something that looks like the result of the chain
rule: the function 1 − x
2 has been substituted into −(1/2)(1 − x)
√
x, and the derivative
#
f(x) = x
f(x) = 3
5
6
f(x)=3-x
f(x) = 1
Domain
3
0
x=2
2
f(x) = 2
Function Equation
f(x) = 5-x
Answers
f(x) = x is a simple linear function with a slope of 1, f(x) = 3 5 6 is a constant function, f(x) = 3-x is a linear function with a negative slope of -1, f(x) = 1 is a constant function, f(x) = 2 is a constant function
What is a constant function?A constant function is a mathematical function whose output value is the same for every input value
From the given parameters, f(x) = x is a simple linear function with a slope of 1, this implies that for every unit increase in x, the value of y increases by 1.
Also, f(x) = 3 5 6 is a constant function, where the value of y is always 3 5 6, regardless of the value of x.
In the same way, f(x) = 3-x is a linear function with a negative slope of -1, which means that for every unit increase in x, the value of y decreases by 1. The fourth function f(x) = 1 is a constant function, where the value of y is always 1, regardless of the value of x.
The domain of the fifth function is 3 0, which means that x can take any value between 3 and 0.
The sixth function f(x) = 2 is a constant function, where the value of y is always 2, regardless of the value of x.
Learn more about domain of a function on https://brainly.com/question/28599653
#SPJ1
Identify the domain and range of the reciprocal function y=2/x+3 +7
Answers
ANSWER:
\(\begin{gathered} \text{ Domain: }\left(-\infty\:,\:-3\right)\cup\left(-3,\:\infty\:\right) \\ \\ \text{ Range: }\left(-\infty\:,\:7\right)\cup\left(7,\:\infty\:\right) \end{gathered}\)STEP-BY-STEP EXPLANATION:
We have the following function:
\(\:y=\frac{2}{x+3}\:+7\)The domain is the input values of the function, in this case, it would be the interval of values that x can take, while the range is the output values of the function, that is, in this case, it would be the interval of values that it can take y.
In the case of a reciprocal function, the domain is affected since the denominator can never be 0 since it generates a mathematical indeterminacy, therefore, we calculate the domain by setting the denominator equal to 0, just like this:
\(\begin{gathered} x+3=0 \\ \\ x=-3 \\ \\ \text{ therefore:} \\ \\ \text{Domain: }\left(-\infty\:,\:-3\right)\cup\left(-3,\:\infty\:\right) \end{gathered}\)The range is affected by the fact that it can never be the value of 7, because the previous expression has no way of making it equal to 0, therefore the range would be:
\(\text{ Range: }\left(-\infty\:,\:7\right)\cup\left(7,\:\infty\:\right)\)According to the graph what is the value of the constant in the equation below? A.03125 B. 3.2 C. 2.2 D.6.6
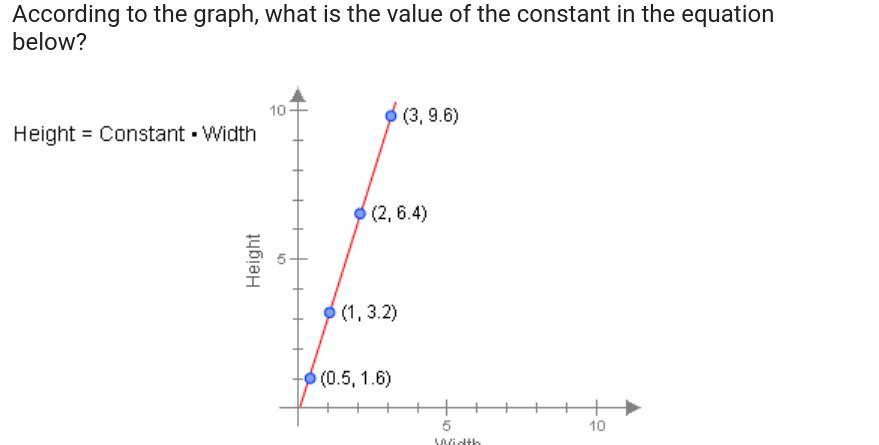
Answers
The value of the constant is 3.2, so the correct option is B.
How to get the value of the constant?
We have a proportional relation of the form:
y = k*x
We want to find the value of k, the constant.
To do that, we can use any of the points shown in the graph.
For example, we can use the first point(0.5, 1.6)
That means that when x = 0.5, we have y = 1.6, replacing that we get:
1.6 = k*0.5
Solving for k:
k = 1.6/0.5 = 3.2
The value of the constant is 3.2, so the correct option is B.
If you want to learn more about proportional relations:
https://brainly.com/question/12242745
#SPJ1
What’s the value of x in centimeters

Answers
Answer:22.5
Step-by-step explanation:
multiply by 1.5
Answer:
22.5 cm
Step-by-step explanation:
Since the triangles are similar, we can use ratios to solve
AC BC
-------- = ---------
FH GH
12 15
-------- = ---------
18 x
Using cross products
12x = 15*18
Divide each side by 12
12x/12 = 15*18/12
x =22.5
Growth and decay how do you solve a(r)to the power of t

Answers
Solution for the question 2 :
It is given that ,
\(\begin{gathered} P_0=\text{ }800 \\ r\text{= }2\text{ \%} \\ n\text{ = 9 years} \end{gathered}\)The population after n years is given by exponential function ,
\(\begin{gathered} P(n)=P_0(1+\frac{r}{100})^n \\ \\ \\ \end{gathered}\)Population after 9 years is calculated as,
\(\begin{gathered} P(9)=\text{ 800 }\times(1+0.02)^9 \\ P(9)=\text{ 800 }\times(1.02)^9 \\ P(9)=800\text{ }\times\text{ 1.1951} \\ P(9)=\text{ }956.08\text{ }\approx\text{ 956 } \end{gathered}\)Thus the population after 9 years is 956 .
Does this table represent a function or not? Why or why not?

Answers
Answer:
D. No, because two of the y-values are the same
Step-by-step explanation:
The y values cannot be the same
Answer:C
Step-by-step explanation:
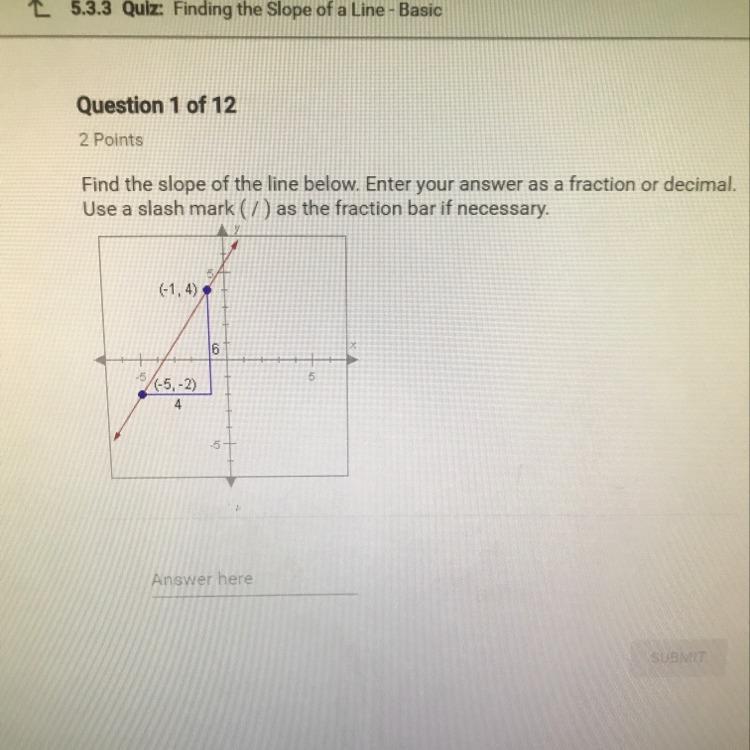
Find the slope of the line below. Enter your answer as a fraction or decimal. Use a slash mark ( / ) as the fraction bar if necessary.
Answers
Answer:
Slope = 2/3
Step-by-step explanation:
From the attached graph :
Point 1 = (-1, 4)
Point 2 = (-5, - 2)
x1 = - 1 ; x2 = - 5
y1 = 4 ; y2 = - 2
Slope = Rise / Run
Rise = (x2 - x1) = - 5 - (-1) = - 5 + 1 = - 4
Run = (y2 - y1) = - 2 - 4 = - 6
Hence,
Slope = - 4 / - 6 = 4 /6 = 2/3
Slope = 2/3
The rectangles in each pair are similar. Find the unknown measures
Answers
IfA={1,2,3,4} B={2,4,6} C={1,3,5,7} andU={1,2,3,4,5,6,7} then B−C
Answers
Answer:
\(B-C=\{2,4,6\}\)
Step-by-step explanation:
We are given the following sets:
\(A=\{1,2,3,4\}\\ B=\{2,4,6\}\\ C=\{1,3,5,7\}\\ and\\U=\{1,2,3,4,5,6,7\}\)
To find: \(B-C = ?\)
Solution:
Here, we are given 4 sets,
The universal set, U and its 3 proper subsets A,B and C.
Proper subsets are the subsets which have at least one element which is extra in the super set.
Now, let us have a look at the definition of 'minus' in terms of sets.
Minus is defined as the set of elements which contains the elements of first set which are not present in the other set.
OR
The common elements are not written.
For example:
P = {10,20,30}
Q = {10,40,70}
P - Q = {20,30}
Common element(s) of P \(\cap\) Q = {10} is/are not written in P-Q.
Here, there are no common elements in B and C.
\(\therefore B-C = B\)
OR
\(B-C=\{2,4,6\}\) is the correct answer.
