Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. y = x^8, y = 1; about y = 3
Answers
Therefore, the volume of the solid of revolution is given by: V = π∫[1,3](y18/8 - 3)2 dy
The given curves are y = x8 and y = 1, and the region to be rotated around the axis of rotation is the region between y = 1 and y = x8, that is, the region bounded by the curves. This region is given by the following figure:
The solid formed is a solid of revolution, and it is given by rotating the region around the line y = 3.
The resulting solid is the portion of the solid that is above the line y = 3.
The distance between y = 1 and y = 3 is 2 units, so the volume of the solid formed by rotating the region about the axis of rotation is given by:
V = π∫[a,b]R2(y)dy
where R(y) is the radius of the disk for a given value of y, which is given by R(y) = x(y) - 3, and x(y) is given by x(y) = y18/8.
Expanding the square, we have:V = π∫[1,3] y183/16 - 6y9/4 + 9 dy
Integrating term by term, we have:
V = π [y218/288 - 6y13/52 + 9y]23 from 1 to 3V
= π [(3)218/288 - 6(3)13/52 + 9(3)] - [(1)218/288 - 6(1)13/52 + 9(1)]23V
= π [2813/288 - 109/13]23
To know more about solid visit:
https://brainly.com/question/32439212
#SPJ11
Related Questions
500m of fencing is available to make 4 rectangular pens of identical shape. Find the dimensions that maximise the area of each pen if the plan is: (DIAGRAMS BELLOW)

Answers
Answer:
The answer is "\(x(\frac{250}{3}-x)\)"
Step-by-step explanation:
Both points are similar that's why the solution is:
\(\to \frac{6x+6y=500}{6}\\\\\to x+y=\frac{250}{3}\\\\\to y= \frac{250}{3}-x \\\\\to Area= xy\\\\ \to Area= x(\frac{250}{3}-x)\)
If the slope of a line and a point on the line are known, the equation of the line can be found using the slope-intercept form, y = mx + b. To do so, substitute the value of the slope and the values of x and y using the coordinates of the given point, then determine the value of b. Using the above technique, find the equation of the line containing the points (-4,7) and (2,-2).
What is the equation of the line?
(Simplify your answer. Type your answer in slope-intercept form. Use integers or fractions for any numbers in the equation.)
Answers
Answer:
y=-3/2x+1
Step-by-step explanation:
NOTE: Doing graphs by hand is a lot easier, it saves a lot more time as well.
Step 1: plot your 2 known points.
Step 2: draw a line that goes between both points
Step 3: find the distance of the points in RISE/RUN format.
-9/6. The slope is negative because the line goes down to the right.
Step 4: find your y-intercept.
1.
Step 5: simplify your equation
-9/6 = -3/2
What is the product?
Enter your answer as a fraction, in simplified form, in the box.
−4/5x10/16
Answers
Answer:
-1/2
Step-by-step explanation:
336,765=3,14×0.55×(l+0.55) please help
Answers
Answer:
l = 194999.45
Step-by-step explanation:
I'm going to assume that you meant 3.14 by 3,14.
336,765 = 3.14 × 0.55 × (l + 0.55)
336,765 ÷ (3.14 × 0.55) = l + 0.55
(336,765 ÷ (3.14 × 0.55)) - 0.55 = l
l = 194999.45
please hellppp please hellllllp

Answers
Answer:
a. 170
b. −25
c. -25
d. 75√3 (Decimal: 129.903811)
What’s the area of this figure?

Answers
The area of the figure given after dividing it to known figures is 58 mm².
Given a figure.
We have to find the area of the figure.
The given figure can be divided in to two rectangles by drawing a horizontal line where the length is increased.
Then we get two rectangles of dimensions,
Length = 6 mm and width = 5 mm
Length = 7 mm and width = 4 mm
Area of the figure = Total area of the two rectangles.
Area of a rectangle = length × width
Area of the figure = (6 × 5) + (7 × 4)
= 30 + 28
= 58 mm²
Hence the area is 58 mm².
Learn more about Area here :
https://brainly.com/question/11952845
#SPJ1
Find the measure of ZSTV.
S
3b
15b + 18
U
T

Answers
Answer:
<stv=153
Step-by-step explanation:
stu+stv=180 (being a straight angle)
3b +15b+18=180
18b=180-18
b=162/18
b=9
now
<stv=15b+18
=15 × 9 +18
=135+18
=153
<stv=153°
Which angles are vertical angles?
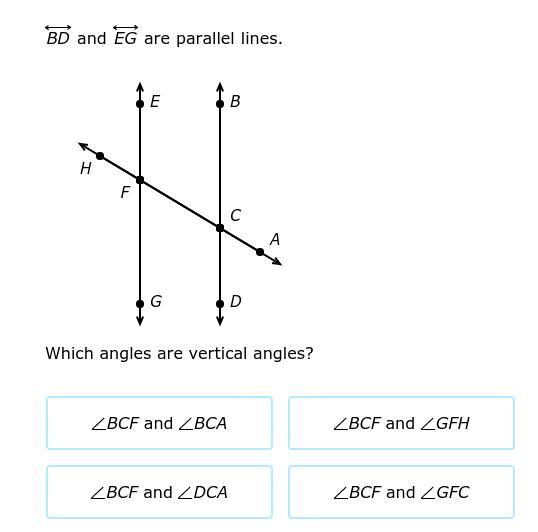
Answers
Answer:
it's between BCF/DCA and BCF/BCA
Are irrational numbers such as π included in the domain of the function f(x) = 7
Answers
Yes, irrational numbers such as π are included in the domain of the function f(x) = 7.
The domain of a function is the set of all possible input values (x) for which the function is defined. In the case of the function f(x) = 7, the output value (y) is always equal to 7, regardless of the input value.
Since every real number, including irrational numbers like π, can be an input value for f(x) = 7, the domain of this function is the set of all real numbers, which includes both rational and irrational numbers. Therefore, π is included in the domain of the function f(x) = 7.
To know more about irrational numbers here
https://brainly.com/question/26862717
#SPJ4
Which of the following represents the series?
–12 + (–5) + 2 + 9 + 16
sum from k equals 0 to 4 of negative 19 plus 7 times k
sum from k equals 1 to 5 of negative 19 minus 7 times k
sum from k equals 0 to 4 of negative 12 plus 7 times k
sum from k equals 1 to 5 of negative 12 minus 7 times k
(image includes proper visuals for each option)

Answers
The expression that represents the sum of the arithmetic series that has a first term of -12, a common difference of +7 and a number of terms of 5 is the option with the following;
\(\sum\limits_{k = 0}^4-12+7\cdot k\)What is an arithmetic series?An arithmetic series one that consists of the sum of an arithmetic sequence, such that each term of the series is obtained from the previous term by the addition or subtraction of a constant.
The series in the question is; -12 + (-5) + 2 + 9 + 16
Each term in the series is obtained from the previous term by the addition of a 7The series in therefore a series of an arithmetic sequence
The equation of the series when the first term is -12 can therefore be presented as follows;
-12 + 7·k
Where;
-12 is the first term, 7 is the common difference, n is the number of terms, and k = n - 1
When n = 1, k = 0, which gives;When k = 0, the expression, -12 + 7·k = -12 + 7 × 0 = -12When k = 1, -12 + 7·k = -12 + 7 × 1 = -5When k = 2, -12 + 7·k = -12 + 7 × 2 = 2When k = 3, -12 + 7·k = -12 + 7 × 3 = 9When k = 4, -12 + 7·k = -12 + 7 × 4 = 16The above values for the terms of the series is obtained by using values of k that range from k = 0 to k = 4
The expression that represents the series is therefore the option;
\(\sum\limits_{k = 0}^4-12+7\cdot k\)Learn more about arithmetic sequence and series here:
https://brainly.com/question/7882626
https://brainly.com/question/6561461
https://brainly.com/question/2289626
#SPJ1
pls help w explanation!!
A town with a population of 5,000 is being divided
into two voting districts: District X and District Y.
The populations of the two districts must differ by no
more than 500 people. Which of the following
systems represents all possible values for the
population x of District X and the population y of
District Y?
A) x-y ≤ 500 and x+y =5,000 B) x-y =500 and x+y ≤ 5,000 C) -500 ≤ x - y ≤ 500 and x+ y =5,000 D) -250 ≤ x - y ≤ 250 and x + y = 5,000
Answers
Answer:
A is the Answer
Step-by-step explanation:
Since the population is being split up into 2 divisions out of 5,000.
This means District X and Y must add up 5000.
\(x + y = 5000\)
District X and Y must differ no more than 500 people.
So this means that X and Y total people difference cannot be over 500 people. So the equation for this is
\(x - y \leqslant 500\)
A shows this so A is the answer.
If the legs of a triangle are 2 and 3 inches can the hypotenuse be 4 inches ?
Answers
Answer:
No
Step-by-step explanation:
The only consecutive integers that satisfy the Pythagorean theorem are 3, 4, and 5.
___
4^2 ≠ 2^2 + 3^2
16 ≠ 4 + 9 . . . . . . . an attempt at applying the Pythagorean theorem to the given numbers fails.
if the price of gasoline is $3.119/gal, what is its price in cents per liter?
Answers
If the price of gasoline is $3.119/gal, then is its price in cents per liter is $68.54 cents/ Liter.
Dimensional Analysis:
The process of performing dimensional analysis is to obtain specific quantities with desired units. With this, we must also be familiar with the construction of the conversion factors needed to find answers to such questions. As we know, a conversion factor can be expressed as a ratio of two parameters with equal values.
We know according to unit:
On converting to galloon
41€ = 41€×(1L/1.3€)× (1qt/1L)× (1gal/4qt)
= (10/1.3)gal
= 8 gallons,
Now,
We convert the given measurement into the desired unit. For this issue, we have implemented the following identities:
100 cents = 1 dollars
1gal = 4.55 liter.
and construct appropriate conversion factors. We proceed with the solution.
$3.119/gal to cents/ liter
$3.119/gal = $3.119/gal × 100 cents/$1 × 1 gal/4.55 Liter
= $ 68.54cents/ Liter.
Learn more about Price:
https://brainly.com/question/19091385
#SPJ4
find the mean of the following numbers
23.25
18.5
15.25
Answers
Answer:19
Step-by-step explanation:

The U-Drive Rent-A-Truck company plans to spend $16 million on 310 new vehicles. Each commercial van will cost $45,000, each small truck $40,000, and each large truck $80,000. Past experience shows that they need twice as many vans as small trucks. How many of each type of vehicle can they buy?
a) Vans__
b) small trucks__
c) large trucks__
Answers
The number of each type of vehicle they can buy is: a) Vans: 160, b) Small trucks: 80, c) Large trucks: 70
Let's denote the number of vans as V, the number of small trucks as S, and the number of large trucks as L. From the given information, we can establish the following equations: V + S + L = 310 (The total number of vehicles is 310), V = 2S (Twice as many vans as small trucks). Now, let's calculate the cost equation based on the cost of each vehicle type: Cost of vans: 45,000 * V, Cost of small trucks: 40,000 * S, Cost of large trucks: 80,000 * L. Since the total cost is $16 million, we have: 45,000V + 40,000S + 80,000L = 16,000,000
Now, we can solve the system of equations: V + S + L = 310 (1), V = 2S (2)
45,000V + 40,000S + 80,000L = 16,000,000 (3). Substituting equation (2) into equation (1), we get: 2S + S + L = 310, 3S + L = 310. Now, we can substitute the value of V from equation (2) into equation (3): 45,000(2S) +
130,000S + 80,000L = 16,000,000 (4). We can now solve the system of equations (3) and (4) to find the values of S and L. Solving equations (3) and (4) simultaneously, we get: 3S + L = 310 (3) 130,000S + 80,000L = 16,000,000 (4). Multiplying equation (3) by 80,000 and subtracting it from equation (4), we eliminate L: 130,000S + 80,000L - 80,000(3S + L) = 16,000,000 - 24,800,000 -110,000S = -8,800,000. Dividing both sides by -110,000, we find: S = 8,800,000 / 110,000, S = 80
Substituting the value of S back into equation (3), we find: 3(80) + L = 310
L = 310 - 240,L = 70. Now that we have the values of S and L, we can find the value of V using equation (2): V = 2S. V = 160. Therefore, the number of each type of vehicle they can buy is: a) Vans: 160, b) Small trucks: 80
c) Large trucks: 70.
To learn more about system of equations, click here: brainly.com/question/30109347
#SPJ11
What is the slope of this line? Responses −34 negative 3 over 4 −3 negative 3 4 4 34 3 over 4 Number graph ranging from negative 5 to 5 on both the x and y axis. A line passes through the point begin ordered pair 0 comma 2 end ordered pair and the point begin ordered pair 4 comma negative 1 end ordered pair
Answers
Answer: The slope would be negative 3/4, so -3/4.
The back to back stem plot shows the number of books read in a year by a group of high school and college students which statements are correct?

Answers
The correct statement are:
The range for high school students is larger than college students.The college median is equal to the high school median.Based on the given information, we can make the following conclusions:
A. The interquartile range for high school students is smaller than college students.
The statement is False
B. The mean for high school students is smaller than college students.
The statement is False because the mean of College is 25.28 and mean for High school is 30.4.
C. The range for high school students is larger than college students.
The statement is True .
D. The college median is equal to the high school median.
The statement is True because the median for both is 24..
E. The mean absolute deviation is larger for college students than high school students.
The statement is False.
Learn more about plot here:
https://brainly.com/question/32275669
#SPJ1
Find the missing side lengths. Leave your answer as radicals in simplest form.

Answers
The values of the sides are;
41. x = 18√3. Option D
42. x = 6√3. Option A
How to determine the valuesUsing the different trigonometric identities, we have;
41. Using the tangent identity, we have;
tan 60 = 9√2/y
cross multiply the values
y =9√2 ×√3
y = 9√6
Using the sine identity;
sin 45 = y/x
1/√2 = 9√6/x
cross multiply the values, we have;
x = 9√2 ×√3 ×√2
x = 18√3
42. Using the cosine identity
cos 60 = 3√3 /x
cross multiply, we have;
x = 6√3
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
BRAINLIEST.... PLS ASAP

Answers
The ratio of the shadow of the building to the building's height is 34 meters / 204 meters = 1/6.
We can set up the following proportion to find the length of the shadow of the tree:
(shadow of the tree) / (height of the tree) = (shadow of the building) / (height of the building)
Solving for the shadow of the tree, we get:
(shadow of the tree) = (shadow of the building) * (height of the tree) / (height of the building)
Substituting in the values we know, we get:
(shadow of the tree) = 34 meters * 12 meters / 204 meters
Simplifying, we get:
(shadow of the tree) = 8.16 meters
So the shadow of the tree is approximately 8.16 meters long.
help me, the question is down below

Answers
Answer:
C
Step-by-step explanation:
6.3/3 = 2.1
12.6/6 = 2.1
18.9/9 = 2.1
-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.--.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-
f(n) = -2n - 2g(n) = 3n-4Find f(n) · g(n)
Answers
Someone please help even if u just answer one of the questions :)

Answers
2(a+2b+3c)= 2a+4b+6c you will distribute the 2 into a, b, and c which you will multiply.
2 x a = 2a
2 x 2b = 4b
2 x 3c = 6c
What steps transform the graph y = x2 to y = x2 + 8
Answers
Answer:
Jun 25, 2018 — Reflection over the y -axis. Vertical stretch by a factor of two. Horizontal translation right two units. Vertical translation up two units. I hope this helps you .. ;]
Step-by-step explanation:
Use the dropdowns to complete the following statement.
The measure of an _____ angle of a triangle is _____ the _____ of its two ____ angles.
First dropdown: corresponding, interior, exterior, alternate
Second dropdown: equal to, less than greater than
Third dropdown: sum, quotient, difference, product
Fourth dropdown: adjacent, supplementary, remote interior, exterior
Answers
Explanation is edge
the distance between the points (a, b) and (c, d) is . so the distance between (2, 3) and (10, 9) is
Answers
The distance between the points (a, b) and (c, d) is √((c - a)^2 + (d - b)^2). And the distance between the points (1, 2) and (7, 10) is 10 units.
The distance between two points (a, b) and (c, d) in a two-dimensional coordinate system can be calculated using the distance formula:
Distance = √((c - a)^2 + (d - b)^2)
In this case, we are given the points (1, 2) and (7, 10), and we need to find the distance between them.
Using the distance formula, we can calculate:
Distance = √((7 - 1)^2 + (10 - 2)^2)
= √(6^2 + 8^2)
= √(36 + 64)
= √100
= 10
Therefore, the distance between the points (1, 2) and (7, 10) is 10 units.
The distance formula is derived from the Pythagorean theorem. It calculates the length of the straight line between two points in a two-dimensional plane. The formula uses the differences between the x-coordinates (c - a) and the y-coordinates (d - b) of the two points and squares them. Then, it takes the square root of the sum of the squares to obtain the final distance.
In our case, we substitute the given coordinates into the formula and perform the calculations step by step. We subtract the x-coordinates and y-coordinates, square the differences, add them together, and finally take the square root of the sum. This gives us the distance between the two points.
The distance between (1, 2) and (7, 10) is found to be 10 units. This means that if we were to draw a straight line connecting these two points on a coordinate grid, the length of that line would be 10 units.
Learn more about coordinate geometry here:
brainly.com/question/18269861
#SPJ11
The correct question is: The distance between the points (a, b) and (c, d) is ________. So the distance between (1, 2) and (7, 10) is __________.
Archimedes drained the water in his tub. 62.562.562, point, 5 liters of water were drained each minute, and the tub was completely drained after 888 minutes.
Answers
Answer:
500 liters
Step-by-step explanation:
We want to find the total amount of water that was drained.
He drained 62.5 liters of water per minute and this went on for 8 minutes. The total amount of water drained is:
62.5 * 8 = 500 liters of water
can someone explain to me how to do this

Answers
Answer:
x=45
Step-by-step explanation:
We know that 2y+6 and 8y-102 are vertical angles to each other. This means that 2y+6=8y-102. \(6y=108\), which means that y=18. \(2\cdot(18)+6=36+6=42\). Since one line is a straight angle, it is 180 degrees we can do \(3x=180-45=135\), so x=45.
Answer:
y = 18
x = 46
measures of the angles:
8y - 102 = 42
2y + 6 = 42
3x = 138
Step-by-step explanation:
So first remember the verticle angles theorem, which states that, when two lines intersect there will be four angles formed; the angles that are opposite from each other will be congruent, that is, they will have the same measure.
Using this we know that opposite angles have to be congruent:
so
(2y + 6) = (8y -102)
now there is an algebra equation that can be solved by inverse operations and simplifying
2y + 6 = 8y - 102
+102 +102
2y + 108 = 8y
-2y -2y
108 = 6y
/6 /6
18 = y
Also, remember that two adjacent angles that form a line will add up to 180,
so
3x + (2y + 6) = 180
*note: I could have also used (8y - 102) but I choose to use (2y + 6)
so now substitute in the value of y that was found
y = 18
3x + (2 * 18 + 6) = 180
simplify
3x + ( 36 + 6) = 180
3x + 42 = 180
now use inverse operations
3x + 42 = 180
-42 -42
3x = 138
/3 /3
x = 46
what is cartesian form
Answers
Answer:
Rectangular Form. A function (or relation) written using (x, y) or (x, y, z) coordinates.
Step-by-step explanation:
??magic
Write the equation of the line that passes through the given points.
(0.-6) and (7.0)
Answers
Step-by-step explanation:
The slope of tghe line (m) = (y₂ - y₁) ÷ (x₂ - x₁)
= (- 6 -0) ÷ ( 0 - 7)
= ⁶/₇
We can now use the point-slope form to write the equation for this line:
y - y₁ = m(x - x₁) where (x₁ , y₁) = (7 , 0)
y = ⁶/₇ ( x - 7 )

Write the equation of the line above in point slope form.

Answers
Answer:
y = 2x - 1
Step-by-step explanation:
Answer:
y=1x+0
Step-by-step explanation:
ur welcome.......