Find the zeros of the function below.
\small -7x=x^2+12
Answers
Answer:
read explanation
Step-by-step explanation:
this is a quadratic equation
first, move the 7x over to the other side so that we have 0 on one side
x^2+7x+12=0
now, we can factor
turn 7x into 3x and 4x, so x^2+3x+4x+12=0
you can turn x^2+3x into x(x+3) and 4x+12 into 4(x+3)
so, our new equation is x(x+3)+4(x+3)=0
that can be turned into (x+4)(x+3)=0 via the distributive property
so, either x+4 or x+3 has to be equal to 0
so, x is either -4 or -3
hope this helped
Related Questions
Which example below describes Newton's Third Law:
Answers
The best description for Newton's third law is: When a passenger stepped from a boat to the shore, the boat moved away from the shore.
What is Newton's third law of motion?Newton's third law of motion states that "For every action, there is an equal and opposite reaction". In other words, if an object A exerts a force on object B, then object B will exert an equal and opposite force back on object A. This is the underlying principle behind the concept of action-reaction pairs.
For example, if you push a wall, the wall will push back on you with an equal force, but in the opposite direction. The law applies to all types of forces, including gravitational, electromagnetic, and strong and weak nuclear forces.
It's important to note that the third law only applies to interactions between two objects. If a third object is involved, the forces will not necessarily be equal and opposite.
Read more on Newton's third law here:https://brainly.com/question/25998091
#SPJ1
A rectangle initially has dimensions 6 cm by 7 cm. All sides begin increasing in length at a rate of 3 cm/s. At what rate is the area of the rectangle increasing after 23 s?
Answers
Answer:
The area of the rectangle is increasing at a rate of 54 cm2/s.
Step-by-step explanation:
what is slope of y=-x+7
Answers
Answer:
y = mx + b
because there is no number in front of the x we automatically assume the answer is 1
so the slope for the equation y = -x + 7 is -1
slope is -1
Step-by-step explanation:
if thats wrong then the slope is 1
hope this helps:)
make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
Lorraine prepared a 2.5-gallon pot filled with tomatoes to be canned in jars. Each jar will hold 1.25 quarts of tomatoes. If 1 gallon equals 4 quarts, how many jars can Lorraine fill?
4 jars
5 jars
8 jars
10 jars
Answers
Answer:
(c) 8 jars
Step-by-step explanation:
You want to know the number of 1.25 quart jars that can be filled from a 2.5 gallon container.
JarsThe number of jars can be found from ...
(2.5 gal) × (4 qt/gal) × (1 jar)/(1.25 qt) = (2.5·4/1.25) jars = 8 jars
Lorraine can fill 8 jars from the 2.5 gallon pot.
<95141404393>
口
5) Place the decimal point in the product.
8 x 0.0006 = 00048
04.8
0.48
0.0048
0.048
Which one is right?
Answers
For what values of a and b is x^64 + ax^b +25 a perfect square for all integer values of x?
Answers
For the expression \(x^64 + ax^b + 25\) to be a perfect square for all integer values of x, b must be 64, and a must be a perfect square, written as a = \(y^2.\)
To determine the values of a and b such that the expression\(x^64 + ax^b\) + 25 is a perfect square for all integer values of x, we need to analyze the properties of perfect squares.
A perfect square is an expression that can be written as the square of another expression. In this case, we want the given expression to be in the form of\((x^n)^2,\) where n is an even integer.
Let's examine the given expression: \(x^64 + ax^b\) + 25
For it to be a perfect square, the quadratic term \(ax^b\)must have the same exponent as the leading term\(x^6^4.\) This means b must be equal to 64.
So we have:\(x^64 + ax^64 + 25\)
Now, we can rewrite this as:\((x^32)^2 + 2(x^32) (\sqrt{a}) + (\sqrt{25})^2\)
By comparing this with the standard form of a perfect square, (\(x^n +\sqrt{k} )^2\), we can deduce that √a must be equal to x^32 and \(\sqrt{25}\) must be equal to \(\sqrt{k.}\)
Therefore, we have: \(\sqrt{a} = x^3^2\)and\(\sqrt{25} = \sqrt{k}\)
From the second equation, we know that k = 25.
Now, substituting the value of k back into the first equation, we have: \(\sqrt{a} = x^3^2\)
To satisfy this equation for all integer values of x, a must be a perfect square. Therefore, we can express a as a =\(y^2\), where y is an integer.
For more such information on: expression
https://brainly.com/question/1859113
#SPJ8
The graph shows a function of the form () = ab
.
Use the drop-down menus to complete the statements about the function, and then write an equation that represents this function.
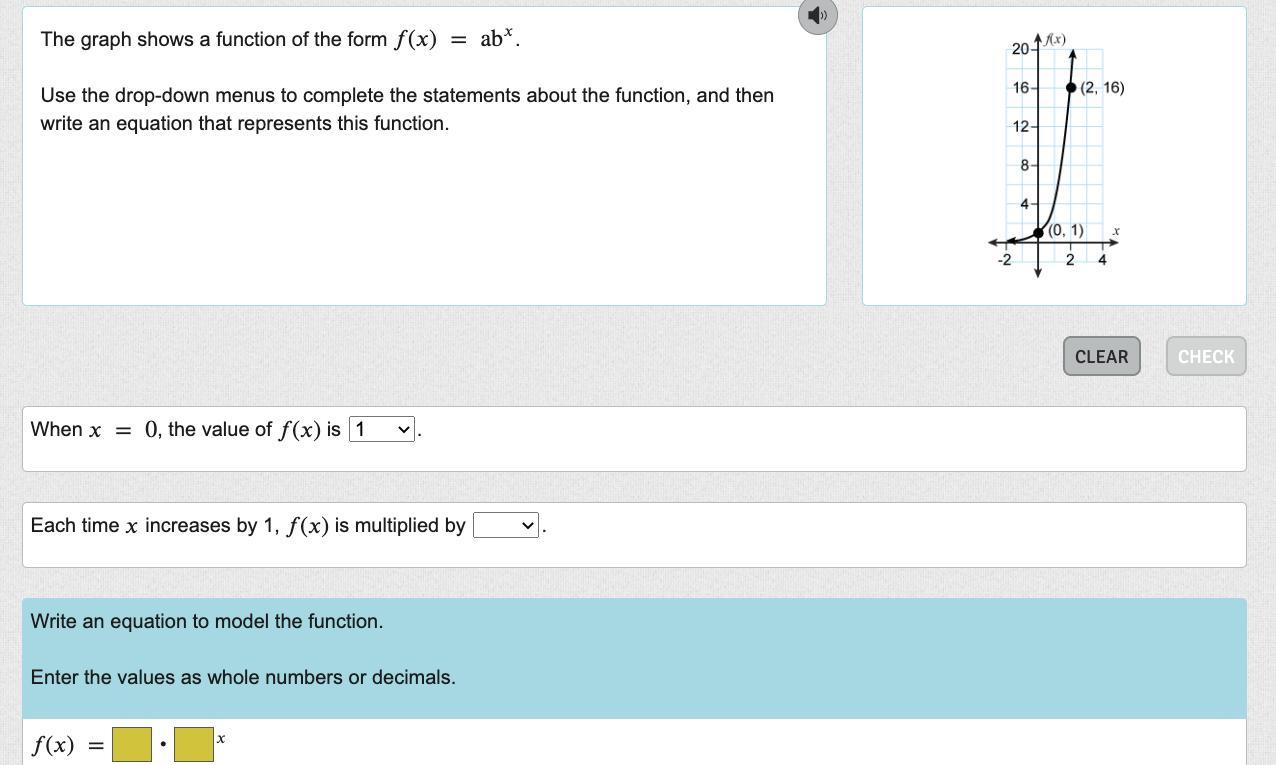
Answers
Answer:
When \(x=0\), the value of f(x) is 1.
Each time x increases by 1, f(x) is multiplied by 4.
Equation of function: \(f(x)=1\cdot 4^x\)
Step-by-step explanation:
The detailed explanation is attached below.

Please help. Will award brainliest

Answers
The dimension of the rectangular of a norman window will be 1.6803*3.3606.
What is the area of Rectangle?
In any quadrilateral which have equal and parallel opposite sides is considered to be a rectangle. It is also called as a polygon with four sides and the four angles that are all 90 degrees each. A rectangle is a shape with only two dimensions. The product of the length and the breadth calculates its area. The length of the diagonals of any rectangle are equal in length. Thus, the length of the diagonals can be calculated easily using the Pythagoras theorem where, the diagonal is considered to be the hypotenuse.
Let r represents the radius, and b be the breadth.
Then, perimeter = 3.14*r+2r+2b = 12
For the dimension needed for the most light to enter we need to maximize the area.
Hence, area of the window : area of the semicircle + area of the rectangle
= \(\frac{3.14*r^2}{2} + 2rb\)
= \(12r - (\frac{3.14+4}{2}) r^2\)
A'(r) = 0
Therefore, \(r=\frac{12}{3.14+4}\) which is nearly equal to 1.6803m
From this value of r we can calculate the value of b to be;
b= 1.6803m
Thus, a= 3.606m
Thus the required dimension is : 1.6803*33606
To know more about semicircle visit:
https://brainly.com/question/30023569
#SPJ1
A sociology professor assigns letter grades on a test according to the following scheme. A: Top 7% of scores B: Scores below the top 7% and above the bottom 60% C: Scores below the top 40% and above the bottom 25% D: Scores below the top 75% and above the bottom 10% F: Bottom 10% of scores Scores on the test are normally distributed with a mean of 67 and a standard deviation of 9.9. Find the minimum score required for an A grade. Round your answer to the nearest whole number, if necessary.
Answers
Answer:66.871
Step-by-step explanation:
The mean=67
The population standard deviation=9.9
Let the minimum score representing grade D above the bottom 10% is x1.
so
P(x<x1)=0.10
P(Z<z)=0.10
z~=-1.48
Please help! A botanist plants an avocado seed and a peach seed and observes the heights over time. The graph shows, in inches, of the avocado tree. The picture has the option to choose from. Should be more than one answer.

Answers
Answer:
the avocado seed was planted deeper below the ground.
the peach tree had a greater average rate of change between the 6th and 10th weeks after being planted.
Step-by-step explanation:
you’re welcome
Find the midpoint of the line segment joining the points (-2, -1) and (-8,12).
Answers
x¹ = -2 x² = -8
y¹ = -1 y² = 12
Using midpoint formula,
M = ( x¹ + x²/2 ,y¹ + ý²/2)
or,M ={ -2+(-8)/2 , (-1) +12/2}
or, =( -10/2 , 11/2)
:M = ( -5 , 11/2)
Parker has 12 blue marbles. Richard has 34
of the number of blue marbles that Parker has.
Part A
Explain how you know that Parker has more blue marbles than Richard without completing the multiplication.
Enter equal to, greater than, or less than in each box.
Multiplying a whole number by a fraction
less than
1 results in a product that is
the original whole number.
Part B
How many blue marbles does Richard have? Enter your answer in the box.
blue marbles
Answers
The table shows the monthly rainfall at a measuring station. What is the mean monthly rainfall? Round your answer to the nearest thousandth.
Answers
The mean monthly rainfall, Rounded to the nearest thousandth, is 2.520 inches.
To determine the mean monthly rainfall, we need to calculate the average of the rainfall values provided in the table. Here is the table:
| Month | Rainfall (in inches) |
|-------|----------------|
| January | 2.3
| February | 1.7
| March | 3.2
| April | 2.9
| May | 2.5
To find the mean monthly rainfall, we add up the rainfall values for each month and divide the sum by the total number of months. In this case, we have five months:
Mean Monthly Rainfall = (2.3 + 1.7 + 3.2 + 2.9 + 2.5) / 5
Calculating the sum of the rainfall values:
Mean Monthly Rainfall = 12.6 / 5
Dividing the sum by the number of months:
Mean Monthly Rainfall = 2.52
Rounded the result to the nearest thousandth, the mean monthly rainfall is approximately 2.520 inches.
Therefore, the mean monthly rainfall, rounded to the nearest thousandth, is 2.520 inches.
To know more about Rounded .
https://brainly.com/question/30545728
#SPJ8
Can someone explain to me why I got this question wrong? The reasoning for my answer (2, 3) for the vertex is because in the setup for the equation f(x) = a( x - h ) + k, x is subtracted from h. If h was negative, it would be adding instead because it'd be a negative and a negative. So I know h is positive. Am I misunderstanding the question? Will give brainliest!

Answers
Kevin's error is that he incorrectly identified the vertex of the parabola as (3, 2) instead of (2, 3), which resulted to the parabola opens downward. The correct vertex is at (2, 3) and the parabola opens upward.
Correcting an Error in Identifying the Vertex and Direction of a Parabola.You are correct that the vertex of the parabola can be determined using the equation f(x) = a(x - h)² + k, where the vertex is at (h, k). In this case, we have f(x) = -(x-2)² + 3, so the vertex can be found by setting x - 2 = 0, which gives x = 2. Plugging this value into the equation,
we get f(2) = -(2-2)² + 3 = 3, so the vertex is at (2, 3).
However, your reasoning for why h is positive is not correct. The expression x - h represents the horizontal distance from the vertex to any point on the parabola. So if x is greater than h, then the expression x - h will be positive, and if x is less than h, then the expression x - h will be negative. In this case, the vertex is at (2, 3), so we have h = 2. This means that any point to the right of the vertex will have a positive value of x - h, while any point to the left of the vertex will have a negative value of x - h.
Therefore, the correct explanation of Kevin's error is that he incorrectly identified the vertex as (3, 2) instead of (2, 3), and as a result, he also incorrectly concluded that the parabola opens downward. In fact, the parabola opens upward because the coefficient of the x² term, -1, is negative.
To know more about the vertex and direction of a parabola,
visit:https://brainly.com/question/20209326
#SPJ1
Nicholas put 1,012 baseball cards into boxes. He put 22 cards in each box. How many boxes did Nicholas need for these baseball cards?
Answers
Answer:
46 boxes
Step-by-step explanation:
1012 / 22 = 46
a vector space must contain at least two vectors.True or false?
Answers
Answer:
False
Step-by-step explanation:
Vector space containing only zero vector.
Answer:
wrong
Step-by-step explanation:
find a polynomial function with the leading coefficient one or negative 1 that has the given zeros multiplicity and degrees 01 multiplicity to 03 multiplicity to degree 4
Answers
The function is negative for since the leading coefficient is positive and the highest degree is odd (9) (-inf, -6).
Find a polynomial function ?The function is negative for since the leading coefficient is positive and the highest degree is odd (9) (-inf, -6).
It then crosses the -6 root to turn positive until it again crosses the -2 root.
(It crosses because the odd multiplicity of both roots)
The function remains negative from -2 until root 4, where it crosses into the positive, where it does not cross since there is an even multiplicity.
In light of the aforementioned, only the first option makes sense. because the leading coefficient is positive and the highest degree is odd (9) the function is negative for (-inf, -6).
Then it crosses the -6 root to become positive until it crosses again the root -2.
To learn more about polynomial function refer
https://brainly.com/question/11378074
#SPJ1
An artist's canvas has sides measuring 3x + 5 and 2x + 1 inches.
What is the area of the canvas? Show all work.
The artist laid the canvas flat on the floor and poured some paint in the center. The paint flows at a rate of r(t) = 2t where t represents time in minutes and r represents how far the paint is spreading on the canvas. The area of the paint can be expressed as A[r(t)]= rur?. What is the area of the circle created by the paint?
If the artist wants the circle to be at least 300 in?, will it be that large in 5 minutes? Support your answer with your work.
Answers
The area of the circle created by the paint is given by the expression 4πt².
The area of the circle is 100π, which is approximately 314.16 in².
The circle will be at least 300 in² in 5 minutes. Yes.
To find the area of the canvas, we multiply the lengths of its sides:
Area = (3x + 5) × (2x + 1)
Expanding the expression:
Area = 6x² + 3x + 10x + 5
Combining like terms:
Area = 6x² + 13x + 5
The area of the canvas is given by the expression 6x² + 13x + 5.
Now, let's find the area of the circle created by the paint.
The area of a circle is given by the formula A = πr², where r represents the radius.
The radius is given by the spreading of paint, which is r(t) = 2t.
Substituting the value of r(t) into the formula, we have:
A[r(t)] = π(2t)²
Simplifying:
A[r(t)] = π(4t²)
A[r(t)] = 4πt²
Now, let's determine if the area of the circle will be at least 300 in² in 5 minutes.
Substitute t = 5 into the area formula:
A[r(5)] = 4π(5)²
A[r(5)] = 4π(25)
A[r(5)] = 100π
Since 314.16 in² is larger than 300 in², the circle created by the paint will be larger than 300 in² in 5 minutes.
For similar questions on area of the circle
https://brainly.com/question/12269818
#SPJ8
A large corporation with monopolistic control in the marketplace has its average daily costs, in dollars, given by
C = 500/x + 200x + x².
The daily demand for x units of its product is given by p= 450,000-100x dollars.
Find the quantity that gives maximum profit.
units
Find the maximum profit.
What selling price should the corporation set for its product?
Answers
Answer:
The profit function can be expressed as:
Profit = Revenue - Cost
Revenue = Price x Quantity
Price = p = 450,000 - 100x
Quantity = x
Cost = C = 500/x + 200x + x²
Substituting these values, we get:
Profit = (450,000 - 100x) x - (500/x + 200x + x²)
Simplifying this expression, we get:
Profit = -x² + 450,000x - 500 - 200x² - x³
To find the quantity that gives maximum profit, we need to differentiate the profit function with respect to x and set it equal to zero:
d(Profit)/dx = -3x² + 450,000 - 400x - 500/x²
Setting this derivative equal to zero and solving for x, we get:
3x³ - 450,000x² + 400x³ + 500 = 0
This equation can be solved numerically to obtain:
x ≈ 98.9
To confirm that this is a maximum, we can check the second derivative of the profit function:
d²(Profit)/dx² = -6x + 800/x³
At x = 98.9, this evaluates to:
d²(Profit)/dx² ≈ -2.71
Since the second derivative is negative, the profit function has a maximum at x ≈ 98.9.
The maximum profit can be found by substituting this value of x into the profit function:
Profit ≈ $20,007,710
To find the selling price that maximizes profit, we can use the demand function:
p = 450,000 - 100x
At x = 98.9, this evaluates to:
p ≈ $35,110
Therefore, the corporation should sell its product for $35,110 to maximize profit.
Compare the best estimate for 1.789/178 and 0.05. Which is less?
Answers
Answer:
The smaller number in 0.01
Step-by-step explanation:
To find this answer, just take the fraction and find the quotient of both numbers.
1.789/178 = 0.01005056179
Now take the quotient and compare it to 0.05.
Is 0.01 larger or 0.05 - the answer is 0.01.
After the party, a bag of ice weighs 7/8 pound. Before the party, the bag of ice weighed 3 times as much. How many pounds did the bac
party?
Drag the pointer to its correct location on the number line to show the weight of the bag of ice before the party.
3
4
Weight of Bag of Ice Before Party
2
4
Finish Late
Answers
The weight before the party could be any positive number
The weight of the bag of ice after the party was 7/8 pounds. So we can set up an equation:
x - weight used at the party = 7/8
We know that the weight used at the party is the weight before the party minus the weight after the party.
So we can substitute 3x for the weight before the party:
3x - (7/8) = weight used at the party
We don't know the exact weight used at the party, but we do know that it was less than or equal to the weight before the party.
So we can set up another inequality:
weight used at the party ≤ 3x
Putting it all together:
3x - (7/8) ≤ 3x
Simplifying:
-(7/8) ≤ 0
To learn more on Inequality click:
https://brainly.com/question/28823603
#SPJ1
3,4,4,5,5,6,6,6,6,7,9,12,14,15 Min: Q1: Med: Q3: Max:
Answers
Answer:
Median ( Q2) = 6
Q1 ( lower quartile) = 4.5
Q3 ( upper quaartile) = 10.5
Step-by-step explanation:
3,4,4,5,5,6, 6,6 ,6,7,9,12,14,15
6,6 is the median but we only need I median. So 6 + 6 = 12, 12 divided 2 = 6.
3,4,4,5,5,6, is the Q1 ( lower quartile ) and median of Q1, is 4,5. 4 + 5 = 9. 9 divided 2 = 4.5
6,7,9,12,14,15 is Q3 ( upper quartile) 9,12 is median but we only need one. So 9 + 12 =21. 21 divided 2 = 10.5
This table represents the gallons of water, g, left in a hot tub after draining it for m minutes.
When graphed, all of the points in the table lie on the same line.
What is the slope and y-intercept of the line?
Drag and drop the slope and y-intercept into the corresponding boxes.
available options are -32, 15,32,480

Answers
Answer:
The answer is slope: -32 y-intercept:480
Step-by-step explanation:
I took the test
Answer: slope -32 y-intercept 480
Step-by-step explanation:
Took the k12 test
HELP IF YOU CAN, THANK YOU :)

Answers
Answer:
(-3, 1, 2, 6, 7)
Step-by-step explanation:
coordinates work like (x,y)
range is the y values
domain is the x values
8) find the values of c that satisfy Rolle's Theorem.
SHOW STEPS

Answers
Hence the value of c = 4 in [3,5] for Rolles theorem.
Rolle's Principle
If a function f is defined in the closed interval [a, b] in a manner that meets the requirements listed below.
The interval [a, b] is closed and the function f is continuous.
ii) On the open interval, the function f can be differentiated (a, b)
iii) If f (a) = f (b), then at least one value of x exists; in this case, let's assume that this value is c, which is situated between a and b, i.e. (a c b), in such a way that f'(c) = 0.
There exists a point x = c in (a, b) such that f'(c) = 0 if a function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b).
let f(x)=x²-8x+12 in [3,5]
i) f(x) is continuous in closed interval [3,5] because f(x) is algebraic function.
ii) f(x) is differentiable in the open interval (3,5) since the algebraic function is differentiable.
now f(3)=3²-8*3+12
f(3)= 9-24+12
f(3)= -3
f(5) = 25-40+12
f(5)= - 3
f(3) = f(5)
f'(x)= 2x-8
x=c ,c in [3,5]
f'(c)= 2c-8
2c-8=0
c=4
Hence the value of c = 4 in [3,5] for Rolles theorem.
learn more about Rolles theorem.
https://brainly.com/question/13972986
#SPJ1
Which statements are true about the graph of y < 2x+1? Check all that apply 3 The slope of the line is 1 The line is solid The area below the line is shaded. A solution to the inequality is (2, 3) The x-intercept of the boundary line is (-2, 0) Graph y
Answers
The statements that are true about the graph of y < 2x+1 include the following:
C. The area below the line is shaded.
D. A solution to the inequality is (2, 3).
What is an inequality?In Mathematics and Geometry, an inequality simply refers to a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the inequality symbols;
Greater than (>).Less than (<).Greater than or equal to (≥).Less than or equal to (≤).Based on the information provided, we have the following equation (inequality);
y < 2x + 1
The slope of the above equation (inequality) is 2 and the y-intercept of the boundary line is (1, 0). Additionally, the area below the dashed line must be shaded because the inequality symbol is less than (<).
Read more on inequality here: brainly.com/question/27976143
#SPJ1

A cafeteria sold 36 cartons of regular flavored milk. If the ratio of regular milk sold to chocolate milk sold was 9:4, what is the combined amount of chocolate and regular milk sold?
Answers
Answer:
The combined amount of chocolate and regular milk sold was 52 cartons.
Step-by-step explanation:
1. Divide
36 ÷ 9 = 4
(This means that the ratio has a unit rate of 4. That means):
2. Second ratio rate
4 x 4 = 16
(Because the unit rate is 4).
3. Add
(Now, we add the original 36 cartons with the 16 cartons we found because the first step was just for finding the unit rate).
36 + 16 = 52 cartons.
May I have Brainliest please? My next rank will be the highest one: A GENIUS! Please help me on this journey to become top of the ranks! I only need 3 more brainliest to become a genius! I would really appreciate it, and it would make my day! Thank you so much, and have a wonderful rest of your day!
A dog shelter is giving away 19 different dogs, but you have room for only 4 of them. How many different dog families could you create?
Answers
The 19 tykes given away by the Shelter, that have room for only 4 tykes per family.
The number of different canine families that could be created from the 19 tykes given away by the sanctum, we need to calculate the number of combinations. room for only 4 tykes , we need to choose 4 tykes from the aggregate of 19 tykes . The order of the tykes in the family doesn't count, as long as we choose different tykes for each family. The number of combinations can be calculated using the formula for combinations C( n, r) = n!/( r!( n- r)!) Where C( n, r) represents the number of combinations of choosing r particulars from a set of n particulars. In this case, we've n = 19( total number of tykes ) and r = 4( number of tykes per family). Plugging these values into the formula, we get C( 19, 4) = 19!/( 4!( 19- 4)!) Calculating the factorial values 19! = 19 × 18 × 17 × 16 × 15 × 14 × 13 × 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = ! = 4 × 3 × 2 × 1 = 24 15! = 15 × 14 × 13 × 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = Substituting these values into the formula C( 19, 4) = /( 24 ×) ≈ 91,390 The 19 tykes given away by the sanctum, considering that you have room for only 4 tykes per family.
To know more about Shelter.
https://brainly.com/question/26279394
#SPJ11
PLSSSSS HELP I HAVE BEEN STUCK ON THIS FOR THE PAST HOUR!!!!!!!!!!!!!!!!!!!!!!!!!
Take a factor out of the square root and simplify the expression:
\(-0.05*\sqrt{28,800}\)
Answers
Answer:
\( - 6 \sqrt{2} \)
Step-by-step explanation:
simplify
\( \sqrt{28800} \)
to
\(120 \sqrt{2} \)
then
-0.05 × 120 = -6
then we have our answer
-6√2