Fish enter a lake at a rate modeled by the function E given by E(t) = 20 + 15 sin(πt/6). Fish leave the lake at a rate modeled by the function L given by L(t) = 4 + 20.1t2. Both E(t) and L(t) are measured in fish per hour, and t is measured in hours since midnight (t = 0).
(a) How many fish enter the lake over the 5-hour period from midnight (t = 0) to 5 A.M. (t = 5)? Give your answer to the nearest whole number.
(b) What is the average number of fish that leave the lake per hour over the 5-hour period from midnight (t = 0) to 5 A.M. (t = 5)?
(c) At what time t, for 0 ≤ t ≤ 8, is the greatest number of fish in the lake? Justify your answer.
(d) Is the rate of change in the number of fish in the lake increasing or decreasing at 5 A.M. (t = 5)? Explain your reasoning.
Answers
Answer: (a) To find the total number of fish that enter the lake over the 5-hour period from midnight to 5 A.M., we need to integrate the rate of fish entering the lake over this time period:
Total number of fish = ∫0^5 E(t) dt
Using the given function for E(t), we get:
Total number of fish = ∫0^5 (20 + 15 sin(πt/6)) dt
Using integration rules, we can solve this:
Total number of fish = 20t - (90/π) cos(πt/6) | from 0 to 5
Total number of fish = (100 - (90/π) cos(5π/6)) - (0 - (90/π) cos(0))
Total number of fish ≈ 121
Therefore, approximately 121 fish enter the lake over the 5-hour period.
(b) To find the average number of fish that leave the lake per hour over the 5-hour period, we need to calculate the total number of fish that leave the lake over this time period and divide by 5:
Total number of fish leaving the lake = L(0) + L(1) + L(2) + L(3) + L(4) + L(5)
Total number of fish leaving the lake = (4 + 20.1(0)^2) + (4 + 20.1(1)^2) + (4 + 20.1(2)^2) + (4 + 20.1(3)^2) + (4 + 20.1(4)^2) + (4 + 20.1(5)^2)
Total number of fish leaving the lake ≈ 257.5
Average number of fish leaving the lake per hour = Total number of fish leaving the lake / 5
Average number of fish leaving the lake per hour ≈ 51.5
Therefore, approximately 51.5 fish leave the lake per hour on average over the 5-hour period.
(c) To find the time when the greatest number of fish are in the lake, we need to find the maximum value of the function N(t) = E(t) - L(t) over the interval 0 ≤ t ≤ 8. We can do this by taking the derivative of N(t) with respect to t and setting it equal to zero:
N'(t) = E'(t) - L'(t)
N'(t) = (15π/6)cos(πt/6) - 40.2t
Setting N'(t) = 0, we get:
(15π/6)cos(πt/6) - 40.2t = 0
Simplifying and solving for t gives:
t ≈ 2.78 or t ≈ 6.22
Since 0 ≤ t ≤ 8, the time when the greatest number of fish are in the lake is t ≈ 2.78 hours after midnight (approximately 2:47 A.M.) or t ≈ 6.22 hours after midnight (approximately 6:13 A.M.).
To justify this, we can use the second derivative test. Taking the second derivative of N(t) gives:
N''(t) = -(15π2/36)sin(πt/6) - 40.2
At t ≈ 2.78, N''(t) is negative, which means that N(t) has a local maximum at this point. Similarly, at t ≈ 6.22, N''(t) is positive, which also means that N(t) has a local maximum at this point. Therefore, these are the times when the greatest number of fish are in the lake.
(d) To determine if the rate of change in the number of fish in the lake is increasing or decreasing at 5 A.M. (t = 5), we need to find the sign of the second derivative of N(t) at t = 5. Taking the second derivative of N(t) gives:
N''(t) = -(15π2/36)sin(πt/6) - 40.2
Plugging in t = 5, we get:
N''(5) = -(15π2/36)sin(5π/6) - 40.2
Simplifying, we get:
N''(5) ≈ -60.5
Since N''(5) is negative, the rate of change in the number of fish in the lake is decreasing at 5 A.M. (t = 5). This means that the number of fish entering the lake is decreasing faster than the number of fish leaving the lake, so the total number of fish in the lake is decreasing.
(a) Approximately 131 fish enter the lake over the 5-hour period from midnight to 5 A.M.
(b) The average number of fish that leave the lake per hour over the same period is approximately 14.8.
(c) The greatest number of fish in the lake occurs at time t = 2.94 hours, or approximately 2 hours and 56 minutes past midnight.
(d) The rate of change in the number of fish in the lake is increasing at 5 A.M.
(a) To find the total number of fish that enter the lake over 5 hours, we need to integrate the function E(t) from t=0 to t=5:
∫[0,5] E(t) dt = ∫[0,5] (20 + 15 sin(πt/6)) dt
This evaluates to approximately 131 fish.
(b) The average number of fish that leave the lake per hour can be found by calculating the total number of fish that leave the lake over 5 hours and dividing by 5:
∫[0,5] L(t) dt = ∫[0,5] (4 + 20.1t^2) dt
This evaluates to approximately 74 fish, so the average number of fish that leave the lake per hour is approximately 14.8.
(c) To find the time at which the greatest number of fish is in the lake, we need to find the maximum of the function N(t) = ∫[0,t] E(x) dx - ∫[0,t] L(x) dx over the interval [0,8]. We can do this by finding the critical points of N(t) and evaluating N(t) at those points. The critical point is at t = 2.94 hours, and N(t) is increasing on either side of this point, so the greatest number of fish is in the lake at time t = 2.94 hours.
(d) The rate of change in the number of fish in the lake at 5 A.M. can be found by calculating the derivative of N(t) at t=5. The derivative is positive, so the rate of change in the number of fish is increasing at 5 A.M.
For more questions like Function click the link below:
https://brainly.com/question/16008229
#SPJ11
Related Questions
The population of racoons in a state park increas by 3.5% each year. Right now, there are estimated to be 280 racoons in the park. How many raccoons will there be in 10 years
Answers
In the next 10 years there will be 398 racoons in the state park
What is population increase?The annual increase in the population size is defined as a sum of differences: the difference between births less deaths and the difference between immigrants less emigrants, in a given country, territory or geographic area at a given year.
Using the formula
p(t) = p(o) e^ kt
k = 3.5/100 = 0.035
t = 10 years
p(t) = 280 e^ 0.035 ×10
p(t) = 280e^0.35
p(t) = 280 × 1.42
p(t) = 398( nearest whole number)
therefore be after 10 years there will be 398 racoons in the state park.
learn more about positive growth from
https://brainly.com/question/1437549
#SPJ1
Solve the following inequality algebraically: negative 2 less-than startfraction x over 3 endfraction 1 less-than 5 a. negative 9 greater-than x greater-than 12 b. negative 9 less-than x less-than 12 c. negative 2 less-than x less-than 5 d. negative 2 greater-than x greater-than 5
Answers
The solution to the inequality algebraically is -9 < x < 12
How to solve the inequality algebraicallyFrom the question, we have the following parameters that can be used in our computation:
negative 2 less-than startfraction x over 3 endfraction 1 less-than 5
Express the statement using numbers and expressions
So, we have the following representation
-2 < x/3 + 1 < 5
Subtract 1 from all sides of the inequality
This gives
-3 < x/3 < 4
Multiply through the inequality by 3
So, we have
-9 < x < 12
Hence, the solution is -9 < x < 12
Read more about inequality at
https://brainly.com/question/25275758
#SPJ1
Answer:
b. Negative 9 less-than x less-than 12
Step-by-step explanation:
in compound time signatures the top number represents the number of beats per measure. select one: true false
Answers
True. In compound time signatures, the top number represents the number of beats per measure. Compound time signatures are typically used for music that has a more complex rhythmic structure, and they are characterized by the subdivision of each beat into three equal parts (known as triplets).
The most common compound time signatures are 6/8, 9/8, and 12/8, with each representing six, nine, and twelve beats per measure respectively.
In 6/8 time, for example, there are two beats per measure, each of which is subdivided into three equal parts. This results in a feeling of two larger beats, each consisting of three smaller beats. In 9/8 time, there are three beats per measure, each of which is subdivided into three equal parts. This results in a feeling of three larger beats, each consisting of three smaller beats. Similarly, in 12/8 time, there are four beats per measure, each of which is subdivided into three equal parts, resulting in a feeling of four larger beats, each consisting of three smaller beats.
Overall, the top number in a compound time signature represents the number of larger beats per measure, while the bottom number represents the duration of each beat (usually an eighth note).
To learn more about time signatures, refer:-
https://brainly.com/question/29729191
#SPJ11
Find the value of X.

Answers
The value of x as required to be determined in the task content is; 10.7°.
What is the value of x?It follows from the task content that the value of x is to be determined from the task content.
Since the given figure is such that the lines MN and MP are tangents to the circle; the assertion which holds is that <MLP and <MNP are supplementary angles.
On this note, it follows that;
73° + x° = 180°.
On this note;
x = 180 - 73
x = 107°.
Read more on supplementary angles;
https://brainly.com/question/98418
#SPJ1
ANOTHER MATH QUESTION TRY YOUR BEST

Answers
Answer:
A) 8inches long and 4 inches wide
Step-by-step explanation:
perimeter is the measurement of the outside of the shape. So for a quilt that'd be 2 lengths and 2 widths. 8+8=16 4+4=8, 16+8=24
what is the lateral surface area of a right circular cylinder with height 10cm and base area 154cmsquare (use pi = 22/7)
Answers
Answer:
Lateral surface area = 154cm²
Step-by-step explanation:
h = 10cm
pi = 22/7
base area = 154cm²
2πrh = 154cm²
2 × 22/7 × r × 10 = 154
440/7 × r = 154
r = 154 ÷ 440/7 = 2.45
r = 2.45
LSA of right circular cylinder = 2πrh
2 × 22/7 × 2.45 × 10
44/7 × 24.5 = 1078/7
1078/7 = 154
Therefore, lateral surface area = 154cm²
Hope it helps:)
please help!
What is/are the vertical asymptote(s) of the function?
y=3x+6x2+2x-35
Answers
Answer:
I don't think there would be any asymptotes because there are no denominators.
Step-by-step explanation:
An exam consists of 16 multiple-choice questions. Each of the 16 answers is either right or wrong. Suppose the probability that a student makes fewer than 5 mistakes on the exam is 0.47 and that the probability that a student makes from 5 to 7 (inclusive) mistakes is 0.14. Find the probability of each of the following outcomes.
The probability that a student makes more than 7 mistakes is
Answers
The probability that a student makes more than 7 mistakes on the exam is 0.39.
What is probability all about?In science, the probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%. T
Now, let X be the number of mistakes a student makes on the exam. Then, the X follows a binomial distribution with n=16 and some unknown probability of success p (i.e., the probability of answering a question correctly).
We know that P(X<5) = 0.47 and P(5<=X<=7) = 0.14. Using the complement rule, we can find P(X>7) as follows:
P(X>7) = 1 - P(X<=7)
= 1 - P(X<5) - P(5<=X<=7)
= 1 - 0.47 - 0.14
= 0.39. Therefore, the probability that a student makes more than 7 mistakes on the exam is 0.39.
Read more about probability
brainly.com/question/24756209
#SPJ1
Please help I’m struggling on this

Answers
Answer:
7. m=3 b=-4
Equation y=3x-4
8. m=-6/4 b=7
Equation y=-6/4x+7
Step-by-step explanation:
Answer:
7. m=3 b= -4 , Equation y=3x-4
8. m= -6/4 b=7 , Equation y=-6/4x+7
Step-by-step explanation:
look in the chart
Leah Deposited $7000 in an account that earns 2% interest compounded annually. How much interest will she have earned after 6 years?
Answers
Answer:
840
Step-by-step explanation:
7000×2×6 ÷ 100. since it is 2%
= 840
Six students are working on math 2/3 of them are working on fractions how many students are working on fractions
Answers
Answer:
4
Step-by-step explanation:
2/3 = 4/6
1/3 = 2
2/3 = 4
3/3 = 6
A health and fitness club instructor's claims that his 3 months special exercise program will significantly reduce weight (in kg). A random sample of 12 persons was selected and these persons were put on the exercise program for 3 months. The weight of each person before and after the 3 months period are analyzed and illustrated in the following output. Std. Error Mean Mean N Std. Deviation 6.095 1.759 Pair 1 Before 86.58012 After 82.973 12 2.954 AL Paired Differences Sig. (2- tailed) t df 95% Confidence Interval of the Difference Std. Mean Deviation Std. Error Mean Lower Upper Before - After B 6.858 1.980 X Y 1.8221 11 .096 a) Identify the statistical analysis used for this study. b) Find the value of A and B. (1 mark) (3 marks) c) Construct a 95% confidence interval for the mean difference in weight before and after the 3 months exercise program. (5 marks) a) Based on the confidence interval in c), can it be concluded that attending the 3 months exercise program will significantly reduce the weight? Give a reason to support your answer. (1 mark)
Answers
Yes, it can be concluded that attending the 3 months exercise program will significantly reduce weight. As the confidence interval doesn't contain zero, which means the difference in weight before and after the exercise program is statistically significant.
a) Statistical analysis used for this study is Paired sample t-test.
b) A is 1.980 and B is 6.858
c) A 95% confidence interval is defined by the formula, CI = (X-Y) ± tα/2 * (S/√n)
Where, X = Mean of weight before starting the exercise program,
Y = Mean of weight after the exercise program,
S = Standard deviation,
tα/2 = t-distribution at alpha level of 0.05,
n = Number of sample pairs
CI = (6.858) ± 2.201 * (1.759/√12)
CI = (6.858) ± 1.784CI = (5.074, 8.642)
Therefore, the 95% confidence interval for the mean difference in weight before and after the 3 months exercise program is (5.074, 8.642).
a) Yes, it can be concluded that attending the 3 months exercise program will significantly reduce weight. As the confidence interval doesn't contain zero, which means the difference in weight before and after the exercise program is statistically significant.
To know more about Statistical analysis visit: https://brainly.com/question/30154483
#SPJ11
What is the area of rhombus ABCD? Enter your answer in the box. Do not round at any steps.

Answers
Answer:
Area of the rhombus ABCD = 16 square units
Step-by-step explanation:
Area of a rhombus = \(\frac{1}{2}(\text{Diagonal 1})(\text{Diagonal 2})\)
From the graph attached,
Diagonal 1 = Distance between the points A and C
Diagonal 2 = Distance between the points B and D
Length of a segment between (x₁, y₁) and (x₂, y₂) = \(\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^2 }\)
Diagonal 1 (AC) = \(\sqrt{(4-0)^2+(-1+1)^2}\) = 4 units
Diagonal 2(BD) = \(\sqrt{(2-2)^2+(3+5)^2}\) = 8 units
Now area of the rhombus ABCD = \(\frac{1}{2}(\text{AC})(\text{BD})\)
= \(\frac{1}{2}\times 4\times 8\)
= 16 units²
Therefore, area of the given rhombus is 16 units².
find the slope of the line that passes through each pair of points. (2,4) and (9,12)
Answers
Considering the expression of a line, the slope of the line that passes through the points (2,4) and (9,12) is 8/7.
What is Linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Knowing two points (x₁, y₁) and (x₂, y₂) of a line, the slope of the line is calculated as:
m= (y₂ - y₁)÷ (x₂ - x₁)
Slope of the line in this caseIn this case, being (x₁, y₁)= (2,4) and (x₂, y₂)= (9,12), the slope m can be calculated as:
m= (12 -4)÷ (9 -2)
Solving:
m= 8÷ 7= 8/7
Finally, the slope of the line is 8/7.
Learn more about the equation of a line having 2 points:
brainly.com/question/16137599
#SPJ1
Which similarity postulate or theorem can be used to verify that the two
triangles shown below are similar?
A. SAS theorem
B. SSS theorem
C. AA postulate
D. Similarity cannot be determined.

Answers
Answer:
C
Step-by-step explanation:
AA postulate because we are given 2 of the 3 angles of each triangle. They are both the same in each triangle. Also, we can find the 3rd angle in each triangle. Since both triangles have the exact same angles, they are similar.
The given triangles ΔABC and ΔLMN are similar by AA postulate.
What is a triangle?A triangle is a three sided polygon that consist of three edges and three vertices .
Here two given triangles are ΔABC and ΔLMN. In these two triangles ∠A=∠L=53° and ∠B=∠M= 72°.
Therefore, the two corresponding angles of triangles ΔABC and ΔLMN are equal . So the third angle of ΔABC is also equal to the corresponding angle of ΔLMN.
Hence two triangles are similar by AA postulate.
Thus two triangles are similar by AA postulate. So option (C) is correct.
To learn more about triagles click here:
https://brainly.com/question/24147586
#SPJ7
Traci mixed nuts and raisins together in bags to make a trail mix. She
had a total of 6 cups of nuts and 8 cups of raisins. She placed 1/3 cup
of nuts in each bag, and 1/4 cup of raisins in each bag. Traci wanted
each bag to have a mixture of nuts and raisins. After Traci uses all
the nuts she has, how many more bags need nuts added?

Answers
Answer:
A) 14
Step-by-step explanation:
Nuts:
\(\frac{6}{\frac{1}{3} }\) = \(\frac{6}{1}\) ÷ \(\frac{1}{3}\) Get a common denominator of 3 and divide
\(\frac{18}{3}\) ÷ \(\frac{1}{3}\) = \(\frac{\frac{18}{1} }{\frac{3}{3} }\) = \(\frac{18}{1}\) = 18
We can make 18 bags with the amount of nuts given.
Raisins:
\(\frac{8}{\frac{1}{4} }\) = 8 ÷\(\frac{1}{4}\) Gert a common denominator of 4 and divide
\(\frac{32}{4}\) ÷ \(\frac{1}{4}\) = \(\frac{\frac{32}{1} }{\frac{4}{4} }\) = \(\frac{32}{1}\) = 32
We can make 32 bags with the amount of raisins given.
32 - 18 = 14
14 more bags need nuts agged.
liam is making chocolate chip cookies. The recipe calls for 1 cup of sugar for every 3 cups of flour. Liam only has 2 cups of flour. How much sugar does liam use?
Answers
1/5 cups of sugar.
have a nice day
what conclusions can be made about the series[infinity] ∑ 3cos(n)/n and the integral test?n=1
Answers
We can make the conclusion that the series ∑ 3cos(n)/n is convergent.
The series ∑ 3cos(n)/n satisfies the conditions of the integral test if we consider the function f(x) = 3cos(x)/x.
Using integration by parts, we can find that the integral of f(x) from 1 to infinity is equal to 3sin(1) + 3/2 ∫1^∞ sin(x)/x^2 dx.
Since the integral ∫1^∞ sin(x)/x^2 dx converges (as it is a known convergent integral), we can conclude that the series ∑ 3cos(n)/n also converges by the integral test.
Using the Integral Test, we can determine the convergence or divergence of the series ∑ (3cos(n)/n) from n=1 to infinity. The Integral Test states that if a function f(n) is continuous, positive, and decreasing for all n≥1, then the series ∑ f(n) converges if the integral ∫ f(x)dx from 1 to infinity converges, and diverges if the integral diverges.
In this case, f(n) = 3cos(n)/n. Unfortunately, this function is not always positive, as the cosine function oscillates between -1 and 1. Due to this property, the Integral Test is not applicable to the given series, and we cannot draw any conclusions about its convergence or divergence using this test.
Learn more about integration here: brainly.com/question/18125359
#SPJ11
Estimate and then solve 6,699 ÷ 72 = ___.
Answers
Answer:
yeah its 93 after being rounded
Step-by-step explanation:
already did it and commented i was just wondering what else there was cause it seemed like there was more.
if tan(x) = − 5 12 and x is in quadrant iv, find the exact values of the expressions without solving for x.
Answers
Given that tan(x) = −5/12 and x is in quadrant IV, we can use trigonometric identities to find the exact values of the expressions without solving for x.
We can begin by drawing a reference triangle in the fourth quadrant, with the opposite side equal to -5 and the adjacent side equal to 12. Using the Pythagorean theorem, we can find the length of the hypotenuse to be 13. Therefore, sin(x) = -5/13 and cos(x) = 12/13.
From these values, we can find the other trigonometric functions as follows:
csc(x) = 1/sin(x) = -13/5
sec(x) = 1/cos(x) = 13/12
cot(x) = 1/tan(x) = -12/5
So, the exact values of the expressions are sin(x) = -5/13, cos(x) = 12/13, csc(x) = -13/5, sec(x) = 13/12, and cot(x) = -12/5.
To learn more about Pythagorean theorem : brainly.com/question/14930619
#SPJ11
question r5 sketch a graph of y = f(x) that satisfies the following requirements on the interval 0 <= x <= 10.
Answers
To sketch a graph of y = f(x) that satisfies the given requirements on the interval 0 <= x <= 10, we need to have more information about the specific requirements of the function. However, we can make some general suggestions for how to approach the problem.
First, we should determine the type of function we are dealing with. Is it linear, quadratic, exponential, trigonometric, or some other type of function? This will affect the shape of the graph and give us an idea of how to start plotting the points.
Next, we should consider any specific points or features that we need to include in the graph. For example, if the function needs to pass through a certain point or have a certain slope, we can use this information to determine additional points on the graph.
Finally, we should make sure that the graph satisfies the given interval of 0 <= x <= 10. This means that the graph should not extend beyond this range, and any points outside of this interval should be excluded.
Overall, to sketch a graph of y = f(x) that satisfies the given requirements on the interval 0 <= x <= 10, we need to carefully consider the function type and any specific requirements, plot the points accordingly, and make sure the graph is within the given interval.
Learn more about graph:
https://brainly.com/question/17267403
#SPJ11
calculator for equation a car left the house traveling north at 10 a.m. another car left the house traveling south two hours later. if the cars traveled at the same rate and were 550 miles apart at 4 p.m., what was the rate of each car ?
Answers
The rate of each car is 55 miles per hour.
In order to find the rate of each car, we need to follow the given steps :
1. Let's denote the rate of each car as R (in miles per hour).
2. The first car traveled north from 10 a.m. to 4 p.m., which is 6 hours. So, the distance covered by the first car can be represented as 6R.
3. T he second car traveled south from 12 p.m. to 4 p.m., which is 4 hours. So, the distance covered by the second car can be represented as 4R.
4. According to the problem, the total distance between the two cars at 4 p.m. is 550 miles. Therefore, the sum of the distances covered by both cars should equal 550 miles.
5. Now, we can set up an equation: 6R + 4R = 550
6. Combine the terms: 10R = 550
7. Solve for R: R = 550 / 10 = 55
So, the rate of each car was 55 miles per hour.
To learn more about equations visit : https://brainly.com/question/2972832
#SPJ11
A) Mo has been rounding decimal numbers to the nearest whole number. Put a * by the correct answers and correct the incorrect answers. Number Rounded to Whole Number Correct (*) or Correction 7.2 7 * 8.5 8 9 12.9 13 * 3.4 3 * 11.5 11 12 9.5 9 10 b) Mo has made the same mistake throughout. Explain to Mo the mistake he has made. A:
Answers
Answer:
A)
7.2 7 * ⇒ correct
8.5 8 9 ⇒ 9 is the correct answer
12.9 13 * ⇒ correct
3.4 3 * ⇒ correct
11.5 11 12 ⇒ 12 is the correct answer
9.5 9 10 ⇒ 10 is the correct answer
B)
When a decimal number is 5 or more, you must round up, e.g. 4.5 must be rounded up to 5. You round down when the number is 4 or less.
PLZ HELP! PLZ EXPLAIN

Answers
Answer:
H. 48
Step-by-step explanation:
Let p represent the number of coins Pamela has. Then 3p is the number Samantha has. After 6 days of adding coins, we have ...
2(p +3·6) = 3p +2·6
2p +36 = 3p +12
24 = p . . . . Pamela has 24 coins; Samantha has 72.
Now, we can find the number of days (d) before the coin count is the same.
24 +3d = 72 +2d . . . . coin counts are the same after d days
d = 48 . . . . . subtract 24+2d
In 48 days from now, Pamela and Samantha will have the same number of coins.
Marvin is making lemon bread and pumpkin bread for a school bake sale. he needs 4 and 1/2 cups of flour for the lemon bread and 1 and 1/2 times as much flour for the pumpkin bread. he only has 2 and 1/8 cups of flour left in his pantry, so he buys a new bag from the grocery store. how much flour will marvin use from the new bag? write your answer as a whole number, fraction, or mixed number. simplify any fractions.
Answers
\(\frac{73}{8}\) cups or \(9\frac{1}{8}\) cups or 9.125 cups of flour will be used from new bag.
Flour required for lemon bread = \(4\frac{1}{2}\) cups
Flour required for lemon bread = \(\frac{(4*2)+1}{2}\)
Flour required for lemon bread = \(\frac{9}{2}\) cups
Flour required for pumpkin bread = \(1\frac{1}{2} * \frac{9}{2}\)
Flour required for pumpkin bread = \(\frac{(2*2)+1}{2}* \frac{9}{2}\)
Flour required for pumpkin bread = \(\frac{5}{2}*\frac{9}{2}\)
Flour required for pumpkin bread = \(\frac{45}{4}\) cups
Now, the amount of flour Marvin already has = \(2\frac{1}{8}\)
The amount of flour Marvin already has = \(\frac{(2*8)+1}{8}\)
The amount of flour Marvin already has =\(\frac{17}{8}\) cups
The amount of flour needed from new bag = \(\frac{45}{4}-\frac{17}{8}\)
Taking LCM, we get 8
The amount of flour needed from new bag = \(\frac{(45*2)-17}{8}\)
The amount of flour needed from new bag = \(\frac{90-17}{8}\)
The amount of flour needed from new bag = \(\frac{73}{8}\) cups
Hence, the amount of flour that will be used from new bag is \(\frac{73}{8}\) cups or \(9\frac{1}{8}\) cups or 9.125 cups.
Learn more about mixed number -
https://brainly.com/question/21610929
#SPJ4
please help me with this its algebra

Answers
The logarithm statement can be written as
log₃9 = log 9/ log 3
log₉ 3 = log 3/log 9
log₂ 8 = log 8/ log 2
log₈2 = log 2/ log 8
What is a logarithm?
The power to which a number must be raised in order to obtain other values is referred to as a logarithm. The easiest way to express large numbers is this way. Numerous significant characteristics of a logarithm demonstrate that addition and subtraction logarithms can also be written as multiplication and division of logarithms.
"The exponent by which b must be raised to yield an is the logarithm of a positive real number a with respect to base b, a positive real number not equal to 1"
Given logarithm are log₃9, log₉ 3, log₂ 8, log₈2.
Apply the formula \(log_ab\) = log b/log a:
log₃9 = log 9/ log 3
log₉ 3 = log 3/log 9
log₂ 8 = log 8/ log 2
log₈2 = log 2/ log 8
To learn more about rule of the logarithm, click on the below link:
https://brainly.com/question/16503695
#SPJ1
Pls answer QUICKLY I need this
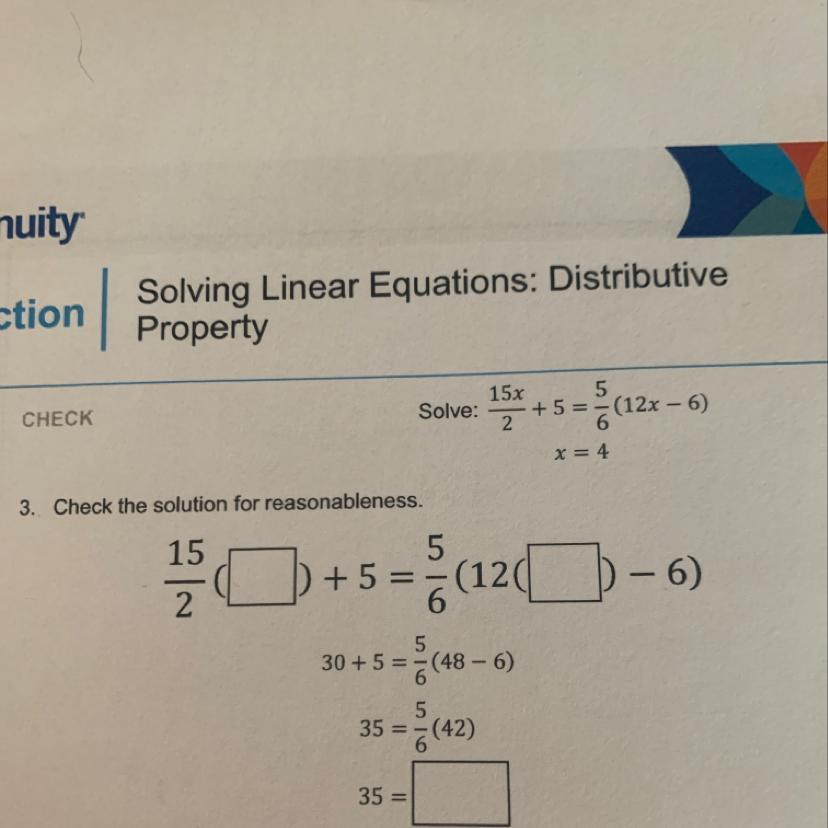
Answers
Answer:
pretty sure this is right

Identify two segments that are marked congruent to each other on the diagram below. ANSWER CORRECTLY !!!!!!!!!!! WILL MARK BRIANLIEST !!!!!!!!!!!! (Two capital letters each )

Answers
Answer: The two angles are supplementary, meaning they add up to 180 degrees.
Therefore:
82 + x = 180
x = 98
x is equal to 98 degrees.
Step-by-step explanation:
Mark me brainlist
hii pls pls help me thank you!

Answers
Answer:
x=61 °
Step-by-step explanation:
angle ABE=90 ° (angle in a semi circle), so angle EBD= angle ABD - angle ABE =115-90=25 °
and the angle EDB=180 - angle EDF =180-86=94 °
so in the triangle BED:
x=180-(angle EDB+ angle EBD) =180-(94+25) =61°
Please help me I will give u 10 points!!

Answers
Answer:
A) 0.25 miles per minute
Explanation:
edge 2021