Five years ago, 45% of registered voters were in favor of Medicare For All, 35% were opposed, and 20% were unsure. This year, a survey of 501 randomly selected registered voters showed that 235 were in favor, 201 were opposed, and 65 were unsure. At the 0.05 level of significance, test the claim that the proportions for all voters have stayed the same as they were 5 years ago.
Answers
The proportions of registered voters in favor of Medicare For All have not remained the same as they were five years ago.
Has there been a change in the proportions of registered voters in favor of Medicare For All?The statistical analysis suggests that the proportions of registered voters in favor of Medicare For All have not remained the same as they were five years ago. To test this claim, a hypothesis test was conducted using a significance level of 0.05.
Five years ago, 45% of registered voters were in favor of Medicare For All, while this year's survey of 501 randomly selected registered voters showed that only 235 individuals (46.9%) were in favor. Similarly, opposition to Medicare For All has increased from 35% to 40.1% (201 out of 501 voters). The percentage of voters who were unsure decreased from 20% to 13% (65 out of 501 voters).
The results of the hypothesis test indicate that there is a significant difference between the proportions observed this year and those from five years ago. The claim that the proportions have remained the same can be rejected.
Learn more about registered voters
brainly.com/question/29581396
#SPJ11
Related Questions
Whats the value of x ?

Answers
need help~giving brainliest!!! and 36pts!
In △△KLM, MK (lines over MK)≅ LM.m∠L=43∘ . Find M.m∠M.
Answers
Answer:
Based on the definition of an isosceles triangle, the measure of angle L is: 43°
An isosceles triangle has two side lengths that are equal in size, and also the angles opposite the equal sides are congruent.
Given that KL ≅ MK in △KLM, it means △KLM is an isosceles triangle.
If m∠M = 43°, therefore, m∠M = m∠L (equal angles directly opposite KL and MK).
This implies that: m∠M = 43°
In summary, based on the definition of an isosceles triangle, the measure of angle M is: 43°
Use the Distributive Property to determine the product of 3x and (x - 5)
Answers
Answer:
3x^2-15x
Step-by-step explanation:
3x(x-5)
3x^2-15x
Graph the function:
y = -3x + 2
Answers
Answer:
Step-by-step explanation:

Find the midpoint of the line segment joining the points corresponding to the complex numbers in the complex plane. 8i, 11-9/ (x, y) =
Answers
The midpoint of the line segment joining the complex numbers 8i and 11 - 9i in the complex plane is (11/2, -1/2) in the form (x, y).
To find the midpoint of the line segment joining the complex numbers 8i and 11 - 9i in the complex plane, we can use the midpoint formula:
Midpoint = (1/2)(z₁ + z₂)
where z₁ and z₂ are the complex numbers.
Given z₁ = 8i and z₂ = 11 - 9i, we can substitute these values into the formula:
Midpoint = (1/2)(8i + 11 - 9i)
Now, let's simplify the expression:
Midpoint = (1/2)(11 - i)
To multiply (1/2) by (11 - i), we distribute the (1/2) to both terms:
Midpoint = (1/2)(11) - (1/2)(i)
Midpoint = 11/2 - i/2
Therefore, the midpoint of the line segment joining the complex numbers 8i and 11 - 9i is (11/2 - i/2). In the form (x, y), the midpoint is (11/2, -1/2).
To learn more about complex numbers visit : https://brainly.com/question/10662770
#SPJ11
Hanna will spend $150 on music festival tickets. Reserved seat tickets cost $25 and general admission tickets cost $10. She wrote the following to represent the situation with a linear equation. What kind of equation did she use?
Answers
Answer: Standard Form
Step-by-step explanation:
In the slope intercept form, you can only solve for one equation at a time.
Ex: y = -2.5x + 15
but when using standard you can easly get the answer for both ticket prices
Ex: 25x + 10y = 150
5r + 2g = 30 is the linear equation that best describes the scenario.
What is a Linear equation?A linear equation is an algebraic equation of the form y=mx+b, where m is the slope and b is the y-intercept, and only a constant and a first-order (linear) term are included. Sometimes, the aforementioned is referred to as a "linear equation of two variables," with y and x serving as the variables.
Given this, Hanna will spend $150 on music festival tickets. Reserved seat tickets cost $25 and general admission tickets cost $10.
Let "r" be the Number of reserved tickets she bought
and "g" be the number of general admission tickets she bought
Money spent od reserved ticket = 25 * r
Money spent in general tickets = 10 *g
Since she totals spent 150$
Thus, the equation will be
25r + 10g = 150
Divide by 5 into both the sides
5r + 2g = 30
therefore, The linear equation that represents the given situation is 5r + 2g = 30.
Learn more about Linear equations here:
https://brainly.com/question/11897796
#SPJ2
a company buys equal numbers of two different card forms. it utilizes 4/5 of one kind and 6/7 of the other. what fraction of the total number is unused?
Answers
12/35 fraction of the total number is unused from two different cards.
What is a fraction?A fraction is written in the form of p/q, where q ≠ 0.
Fractions are of two types they are proper fractions in which the numerator is smaller than the denominator and improper fractions where the numerator is greater than the denominator.
Assuming the total first kind of card form is 1 and the total second kind of card form is also one.
Given, a company buys equal numbers of two different card forms. it utilizes 4/5 of one kind and 6/7 of the other.
∴ The total unused card form is,
= (1 + 1) - (4/5 + 6/7).
= 2 - (28 + 30)/35.
= 2 - 58/35.
= (70 - 58)/35.
= 12/35.
learn more about fractions here :
https://brainly.com/question/10354322
#SPJ1
A bank officer wants to determine the amount of the average total monthly deposits per customer at the bank. He believes an estimate of this average amount using a confidence interval is sufficient. How large a sample should he take to be within $200 (MOE) of the actual average with 99% confidence? He assumes the standard deviation of total monthly deposits for all customers is about $1000
Answers
After calculating and analyzing the given question, the bank officer should be inclined to take a sample of at least 133 under the condition of within $200 (MOE) of the actual average with 99% confidence.
In the event of determining the size sample needed for understanding average total monthly deposits by implementing the formula
n = (z x Σ / E)²
here,
n = sample size,
z = z-score involving the desired level of confidence,
Σ = population standard deviation,
E = margin of error
Staging the values in the formula
n = (2.576 * 1000 / 200)² = 132.71
≈ 133
After calculating and analyzing the given question, the bank officer should be inclined to take a sample of at least 133 under the condition of within $200 (MOE) of the actual average with 99% confidence.
To learn more about monthly deposits,
https://brainly.com/question/31112326
#SPJ4
If
F(x)=3x-2
and
G(x)=x−5
, what is
F(x)⋅g(x)
Answers
The composite function f(x). g(x) is represented as 3x² - 17x + 10
How to find composite function?The composite function can be solved as follows:
f(x) = 3x - 2
g(x) = x - 5
Therefore, the composite function f(x). g(x) is as follows:
f(x). g(x) = f(x) × g(x)
Hence,
f(x) × g(x) = (3x - 2)(x - 5)
f(x) × g(x) = 3x² - 15x - 2x + 10
f(x) × g(x) = 3x² - 17x + 10
Therefore, the function f(x) × g(x) = 3x² - 17x + 10
learn more on functions(f(x)) here: https://brainly.com/question/14626983
#SPJ1
Find the average rate of change of the function f(x) = 2x² - 6x-1, on the interval z € [0,4]. Average rate of change Give exact answer! Submit Question Jump to Answer
Answers
The average rate of change of the function f(x) = 2x² - 6x - 1 on the interval [0,4] is -14.
To find the average rate of change of a function on an interval, we need to calculate the difference in function values at the endpoints of the interval and divide it by the difference in the corresponding x-values. In this case, the interval is [0,4].
Evaluate the function at the endpoints of the interval:
f(0) = 2(0)² - 6(0) - 1 = -1
f(4) = 2(4)² - 6(4) - 1 = 15
Calculate the difference in function values:
Δf = f(4) - f(0) = 15 - (-1) = 16
Calculate the difference in x-values:
Δx = 4 - 0 = 4
Find the average rate of change:
Average rate of change = Δf / Δx = 16 / 4 = 4
Therefore, the average rate of change of the function f(x) = 2x² - 6x - 1 on the interval [0,4] is
To learn more about average- brainly.com/question/10945539
#SPJ11
What is the solution to 3 x 2. 4 greater-than-or-equal-to 3. 0? x greater-than-or-equal-to 0. 2 x greater-than-or-equal-to 0. 6 x greater-than-or-equal-to 1. 8 x greater-than-or-equal-to 2. 5.
Answers
Answer:
Excuse me if this is wrong but I think you have to multiply 3 x 2.4 which is 7.2 and that is greater that 3.0.
Step-by-step explanation:
In constructing a confidence interval for a mean with unknown variance with a sample of 25 items, Beth used z instead of t. "Well, at least my interval will be wider than necessary, so it was a conservative error." said she Is Beth's statement correct? Multiple Choice Yes It depends on u. O No.
Answers
Beth's statement is incorrect.
The main answer: No.
Is Beth's statement about using z instead of t correct?Using the z-distribution instead of the t-distribution when constructing a confidence interval for a mean with unknown variance can lead to an incorrect interval width. The t-distribution takes into account the sample size, which is particularly important when the sample size is small. By using the z-distribution, which assumes a large sample size or known variance, the resulting interval may be narrower than necessary. This means that the interval might not capture the true population mean with the desired level of confidence.
Learn more about variance
brainly.com/question/31432390
#SPJ11
What’s the answer to “factor x^2+11x+30”
Answers
Answer:
(x+5)(x+6)
Step-by-step explanation:
Used the AC method which uses the form of ax²+bx+c
In Exercises 57-60 \( \square \), write the given system of linear equations as a matrix equation. 57. \( \left\{\begin{array}{r}3 x+2 y=-1 \\ 7 x-y=\quad 2\end{array}\right. \)
Answers
The matrix equation for Exercise 57 is:
\[ \begin{bmatrix} 3 & 2 \\ 7 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} \]
In Exercise 57, we are asked to write the given system of linear equations as a matrix equation.
To do this, we need to separate the coefficients of the variables and the constants from the equations and write them in matrix form. The coefficients of the variables will form the coefficient matrix, and the constants will form the constant matrix.
The coefficient matrix will be a 2x2 matrix, with the first row containing the coefficients of x and y from the first equation, and the second row containing the coefficients of x and y from the second equation. The constant matrix will be a 2x1 matrix, with the first row containing the constant from the first equation, and the second row containing the constant from the second equation.
So, the matrix equation for the given system of linear equations will be:
\[ \begin{bmatrix} 3 & 2 \\ 7 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} \]
Therefore, the matrix equation for Exercise 57 is:
\[ \begin{bmatrix} 3 & 2 \\ 7 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} \]
Learn more about linear equations
brainly.com/question/11897796
#SPJ11
The diagram shows a rectangle. The area of the rectangle is 310 m². Work out the value of w when 5x-9 is the length and 3x+7 is the another length
Answers
Answer:
w = 10
Step-by-step explanation:
First we take the two values for the breadth of the rectangle
So:
5x - 9 = 3x + 7
now we solve this equation as follows:
5x - 3x = 9 + 7
2x = 16
x = 8
now that we have found the value for x, we can substitute it in the equation, 5x - 9,or in the equation, 3x + 7.
when we substitute x in any of these equations, we get
5(8) - 9 = 31
3(8) + 7 = 31
now that we have the value for the breadth we can form the following equation:
31 × w = 310
31w = 310
w = 310/31 = 10
Answer:
10
Step-by-step explanation:
Firstly, we find the value of X
since 5X-9 and 3X+7 are lenghts
5X-9= 3X+7
5X-3X= 7+9
2X = 16
dividing bothsides by 2
2X/2= 16/2
X = 8
Hence,
5X-9= 5(8)-9= 40-9 = 31
3X+7=3(8)+7= 24+7= 31
To find the width
Area= lenght×width
310= 31×w
31w= 310
w= 310/31
W= 10
What is the solution of the inequality shown
below?
y+7≤-1
Answers
The solution to the inequality is y ≤ -8. This means that any value of y that is less than or equal to -8 will satisfy the original inequality.
To solve the inequality y + 7 ≤ -1, we need to isolate the variable y on one side of the inequality sign.
Starting with the given inequality:
y + 7 ≤ -1
We can begin by subtracting 7 from both sides of the inequality:
y + 7 - 7 ≤ -1 - 7
y ≤ -8
The solution to the inequality is y ≤ -8. This means that any value of y that is less than or equal to -8 will satisfy the original inequality.
In the context of a number line, all values to the left of -8, including -8 itself, will make the inequality true. For example, -10, -9, -8, -8.5, and any other value less than -8 will satisfy the inequality. However, any value greater than -8 will not satisfy the inequality.
For such more question on solution:
https://brainly.com/question/24644930
#SPJ8
The following question may be like this:
What is a solution of the inequality shown below? y+7≤-1
An airplane is at an altitude of 1200 m, the angle of depression to a building at the airport on the ground measures 28∘. Find the distance from the plane to the building. Round your answer to the nearest tenth. Hint: Find the hypotenuse.
The distance from the plane to the building is _________ meters.
Answers
Answer:
The distance from the plane to the building is ___2553.2___meters.
Step-by-step explanation:
Given that An airplane is at an altitude of 1200 m.
The angle of depression to a building at the airport on the ground measures 28°.
We need to find the distance from the plane to the building.
Please check the attached diagram.
Let 'x' be the required distance in meters.
It forms a right-angled triangle as shown in the attached diagram.
The angle = Ф = 28°
The opposite to angle = 1200 meters
All we need to find the hypotenuse to determine the distance from the plane to the building.
Using the trigonometric ratio
sin θ = Perpendicular ÷ Hypotenuse
sin (28°) = 1200 ÷ x
x = 1200/sin (28°)
= 1200 / 0.47 ∵ sin (28°) = 0.47
= 2553.2 m
Thus, the distance from the plane to the building is ___2553.2___meters.

In square ABDC, if BC=8, what is x
Answers
the answer is 4 square root of 2

The plane is equipped with an orthogonal frame (0, i, j).
Let (d) be the line with cartesian equation:
(d) : 2x-3y+1=0 and A(-4,3)
Find the coordinates of the orthogonal projection of A on the (d).
Answers
Answer:
what
Step-by-step explanation:
you know you should drink some water. 75% of americans are dehydrated and don't know it. being hydrated will fix your problems. because being dehydrated will make you not able to do simple math :)
Miles has 10 red marbles, 3 blue marbles and 5 green marbles. He randomly chooses a marble out of a bag 150 times. Make a prediction of how many times Miles will pull a green marble
A Close to but not exactly 30
B Close to but not exactly 300
C Close to but not exactly 90
D Close to but not exactly 45
Answers
Answer:
D
Step-by-step explanation:
Solve the system of equations by substitution. Simplify your answer. Write the
solution as an ordered pair.
y= 3x - 13
3x + 2y = 19
Answers
Answer:
x = 5 y = 2
Step-by-step explanation:
3x + 2(3x - 13) = 19
3x + 6x - 26 = 19
9x = 45
x = 5
y = 3(5) - 13
y = 15 - 13
y = 2
Read the word problem below.
Antonio has a total of 55 marbles. He has 15 green marbles and 12 red marbles. The rest of the marbles are blue. How many blue marbles does he have?
A student solves this problem by writing an equation. Which strategy could help check the student’s answer?
Check that the sum of the final answer, 12, and 15 is 55.
Check that the difference of 55 and the final answer is 12.
Check that the sum of the final answer, 27, and 15 is 55.
Check that the difference of 55 and the final answer is 15.
This is just built different. Thank you so much if you can figure it out!!!!!
Answers
Step-by-step explanation:
I dont know how to choose the answer but I will give my own opinion..
total marble=55
green=15
red=12
blue=?
so: 55-12+15
blue=55-27
so blue =28..
sorry if it is wrong
Answer:
A
Step-by-step explanation:
How to use interp2 to resize arrays of different sizes?
Answers
Interp2 is a MATLAB function that can be used to resize arrays of different sizes. This function is especially useful when we want to change the dimensions of an array without losing any important data.
An array is a collection of values or elements arranged in a specific order. When we want to resize an array, we essentially want to change its shape, but keep the same amount of data. This can be tricky when dealing with arrays of different sizes, because we need to find a way to map the data from one array onto another.
Interp2 helps us do this by using interpolation. Interpolation is a mathematical technique that allows us to estimate values between known data points. In the context of array resizing, interpolation is used to estimate the values of the new array based on the values of the old array.
To use interp2 to resize arrays, we need to provide it with the following inputs:
The old array (the array we want to resize)
The new size of the array (the dimensions of the new array)
The method of interpolation (how we want to estimate the values of the new array)
For example, let's say we have an array A that is 4x4, and we want to resize it to a 6x6 array. We can use interp2 as follows:
B = interp2(A, 6, 6, 'cubic');
In this case, we are telling interp2 to resize the array A to a 6x6 size using cubic interpolation. The resulting array B will have the same amount of data as A, but will be reshaped to fit the new dimensions.
To know more about array here.
https://brainly.com/question/19570024
#SPJ4
Melinda can paint 14 of a wall in the same time that desiree can paint 25 of a wall. How much of a wall will melinda have painted when desiree has finished painting 1 wall?.
Answers
Melinda will have painted 56 percentage of a wall for the time taken by Desiree, when she has finished painting 1 wall.
The computation of the difference between the time taken by Desiree and Melinda to paint walls at their respective speeds can be shown using the generalized calculations, as expressed hereunder,
Desiree will take 4x the time for painting 1 wall completely (25x4=100%). Thus, the amount of time taken by Melinda will also be 4x of her actual time, as below,
14×4= 56%
Therefore, Melinda will have covered 56 percent of the wall in the time when Desiree completes painting the entire wall.
Learn more about time taken here:
https://brainly.com/question/16963199
#SPJ4
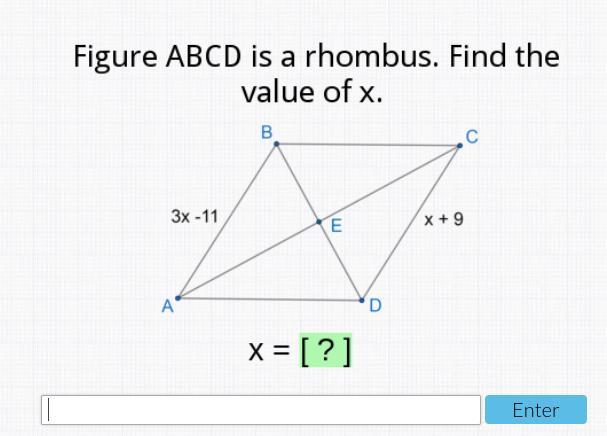
Figure abcd is a rhombus. find the value of x
Answers
Answer:
The answer would be x =10
Step-by-step explanation:
Fill in 10
You welcome
The value of x in the figure ABCD is 10.
What is a rhombus?We know that rhombuses are a particular type of quadrilateral in Euclidean geometry. It is a unique instance of a parallelogram in which the diagonals meet at a 90-degree angle and all sides are equal.
How to solve it?Since the side lengths of a rhombus are equal, so the lengths of AB and DC are equal.
Now, 3x - 11 = x + 9
i.e. 3x - x = 9 + 11
i.e. 2x = 20
i.e. x = 10
Therefore the value of x in the figure ABCD is 10.
Learn more about rhombus here -
https://brainly.com/question/14393368
#SPJ2
PLEASE HELP
WILL GIVE BRAINLIEST
AND 5.0 RATING
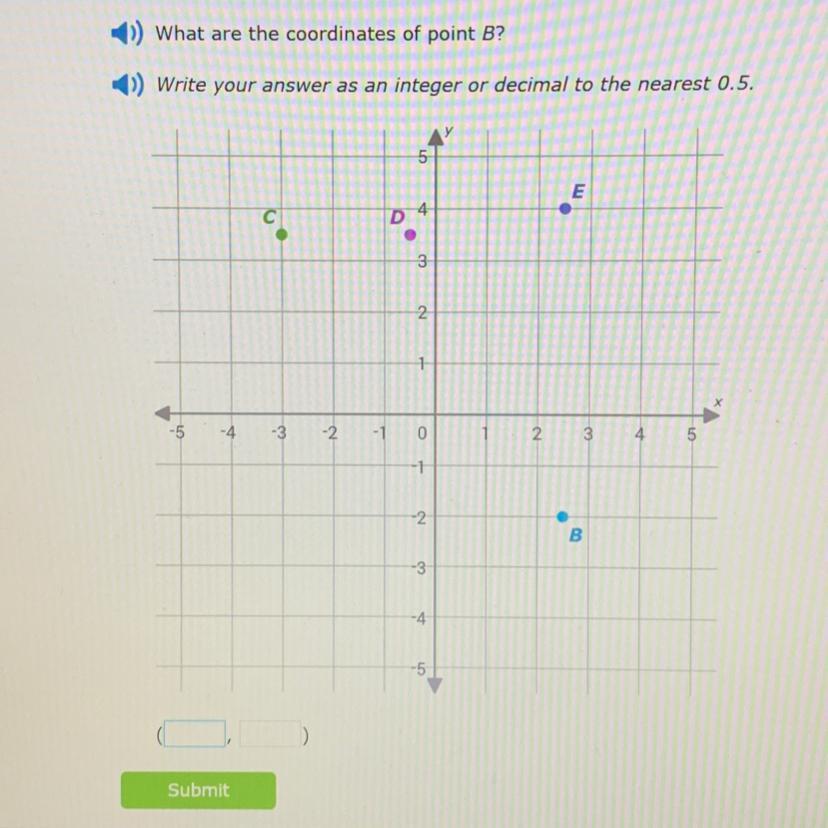
Answers
Answer:
2.5, -2
Explanation:
The coordinate of y is -2 & the coordinate of x is 2.5.
solve The Following Using The Distributive Property
(-75) x173+173x(-25)
Answers
you start by multiplying (-75) by 173 and you get -12975. you then multiplying 173 by (-25) and you get -4325
the overall answer is -17300
Answer:
Step-by-step explanation:
(-75) x173+173x(-25)
173(-75-25)
173(-100)
-17300
the sales-tax rate in new york is 8 and 1/4%. how much city sales tax would be charged on a purchase of $428.86? what will be the total cost of the purchase
Answers
Answer:
$464.24095
Step-by-step explanation:
8 1/4% = NY sales-tax rate
8 1/4 % = .0825
428.86 x .0825 = 35.38095
428.86 + 35.38095 = $464.24095
Reuben's gas tank is 1/6
full. After he buys 11 gallons of gas, it is 2/3
full. How many gallons can Reuben's tank hold?
Answers
(1/6)x + 11 = (2/3)x
by solving we find:
x = 22 gal
Suppose that the coefficient matrix of a homogeneous system of equations has a column of zeros. Prove that the system has infinitely many solutions. Hint: What are the possibilities for the number of solutions to a linear system of equations? Can you definitively rule out any of these?
Answers
A homogeneous system of equations with a column of zeros in the coefficient matrix has infinitely many solutions because one of the variables can take any value without affecting the system, creating a free variable that leads to infinite solutions.
To prove that a homogeneous system of equations with a column of zeros has infinitely many solutions, let's follow these steps:
1. Recall that a homogeneous system of equations is a linear system in the form Ax = 0, where A is the coefficient matrix, x is the variable vector, and 0 is the zero vector.
2. Consider a system with a column of zeros in the coefficient matrix A. This means one of the variables has no effect on the system, as its coefficients are all zeros.
3. A linear system of equations can have either no solutions, one unique solution, or infinitely many solutions. However, in a homogeneous system, there's always at least one solution: the trivial solution where all variables are equal to zero (x = 0).
4. Since one of the variables has a column of zeros in the coefficient matrix, we can assign any value to that variable without affecting the system, as the sum of the products of its coefficients and the variable will always be zero.
5. This means we have a free variable, which can take infinitely many values. Consequently, the system must have infinitely many solutions.
In conclusion, a homogeneous system of equations with a column of zeros in the coefficient matrix has infinitely many solutions because one of the variables can take any value without affecting the system, creating a free variable that leads to infinite solutions.
To learn more about “coefficients” refer to the https://brainly.com/question/1038771
#SPJ11