for a in exercise 6, part (b) and b = [30, 30, 20], if ax = b has the given solution x' [10, 10, 0, o], find the family of all solutions to ax = b.
Answers
the family of all solutions is:
x = [10, 10, 0] + t [2/3, 1/3, 1]
where t is any scalar. This is the general solution to the system Ax = b.
In exercise 6, part (b), we found that the reduced row echelon form of the augmented matrix [A | b] is:
[1 0 0 | 10]
[0 1 0 | 10]
[0 0 1 | 0 ]
This tells us that the system of equations Ax = b has a unique solution x' = [10, 10, 0]. To find the family of all solutions, we need to consider the homogeneous system Ax = 0, where the right-hand side vector is zero.
The augmented matrix of this system is:
[1 1 -1 | 0 ]
[2 -1 1 | 0 ]
[1 1 -1 | 0 ]
We can row-reduce this matrix to find the reduced row echelon form:
[1 0 -2/3 | 0 ]
[0 1 -1/3 | 0 ]
[0 0 0 | 0 ]
The solution set to the homogeneous system Ax = 0 can be expressed in terms of the free variable as:
x = t [2/3, 1/3, 1] where t is any scalar.
To find the family of all solutions to Ax = b, we add the particular solution x' to the solution set of the homogeneous system. Therefore, the family of all solutions is:
x = [10, 10, 0] + t [2/3, 1/3, 1]
where t is any scalar. This is the general solution to the system Ax = b.
To know more about homogeneous system, refer here:
https://brainly.com/question/30504189
#SPJ11
Related Questions
The perimeter of a standard-sized rectangular rug is 36 ft. The length is 2 ft longer than the width. Find the dimensions.
Answers
Answer and Step-by-step explanation:
The length is 10 and the width is 8
You have $561 in your checking account. You spend part of this money on booking the hotel room. You now have $187 in your account. How much was the cost of the hotel room? D F 3 374
Answers
Answer:
$374
Step-by-step explanation:
561-187=374
What would you choose as x in the given series of clicks to calculate formulas automatically: file < options < x < automatic?
Answers
We should choose Formulas as X in the given series of clicks to calculate formulas automatically.
File < Options < (A) Formulas < Automatic
What are Formulas?In science, a formula is a concise way of symbolically expressing information, such as a mathematical formula or a chemical formula. In science, the term formula refers to the general construct of a relationship between given quantities. In mathematics, a formula is an identity that equates one mathematical expression to another, the most important of which are mathematical theorems. A formula (also known as a well-formed formula) is a logical entity that is constructed using the symbols and formation rules of a given logical language.We should choose Formulas as X in the given series of clicks to calculate formulas automatically.
Therefore, File < Options < (A) Formulas < Automatic
Know more about Formulas here:
https://brainly.com/question/21140562
#SPJ4
The complete question is given below:
What would you choose as X in the given series of clicks to calculate formulas automatically: File < Options < X < Automatic?
a. Formulas
b. Language
c. Proofing
d. Advanced
In 12 years, Janice will be 8 times as old as she was 2 years ago. How old is Janice
now?
Answers
Janice is currently 4.
In 12 years, Janice will be 16, and 2 years ago she was 2. That being said, 16 is eight times more than 2, thus meaning she is currently 4 years old.
I hope this helps!
Which operation will solve the following word problem? Jeff earns $14.00 per hour, Tom earns half as much as Jeff. How much does Tom earn per hour?
a.) Multiplication
b.) Subtraction
c.) Addition
d.) Division
Answers
Answer:
Multiplication
Amount Tom earns per hour = $7
Step-by-step explanation:
Amount Jeff earns per hour = $14
Amount Tom earns per hour = 1/2 × $14
Note: 1/2 = 0.5
Amount Tom earns per hour = 1/2
× $14
= 0.5 × $14
= $7
Amount Tom earns per hour = $7
change 4-1/2 to a improper fraction
Answers
Answer: 9/2
Step-by-step explanation: Hope this helps.
The curved sides of large storage tanks at a refinery need to be painted. What is the approximate area of each tank that will be painted?
OA. 9,500 ft²
OB. 1,144 ft²
OC. 4,574 ft²
OD. 2,287 ft²

Answers
On a time limit for Geometry
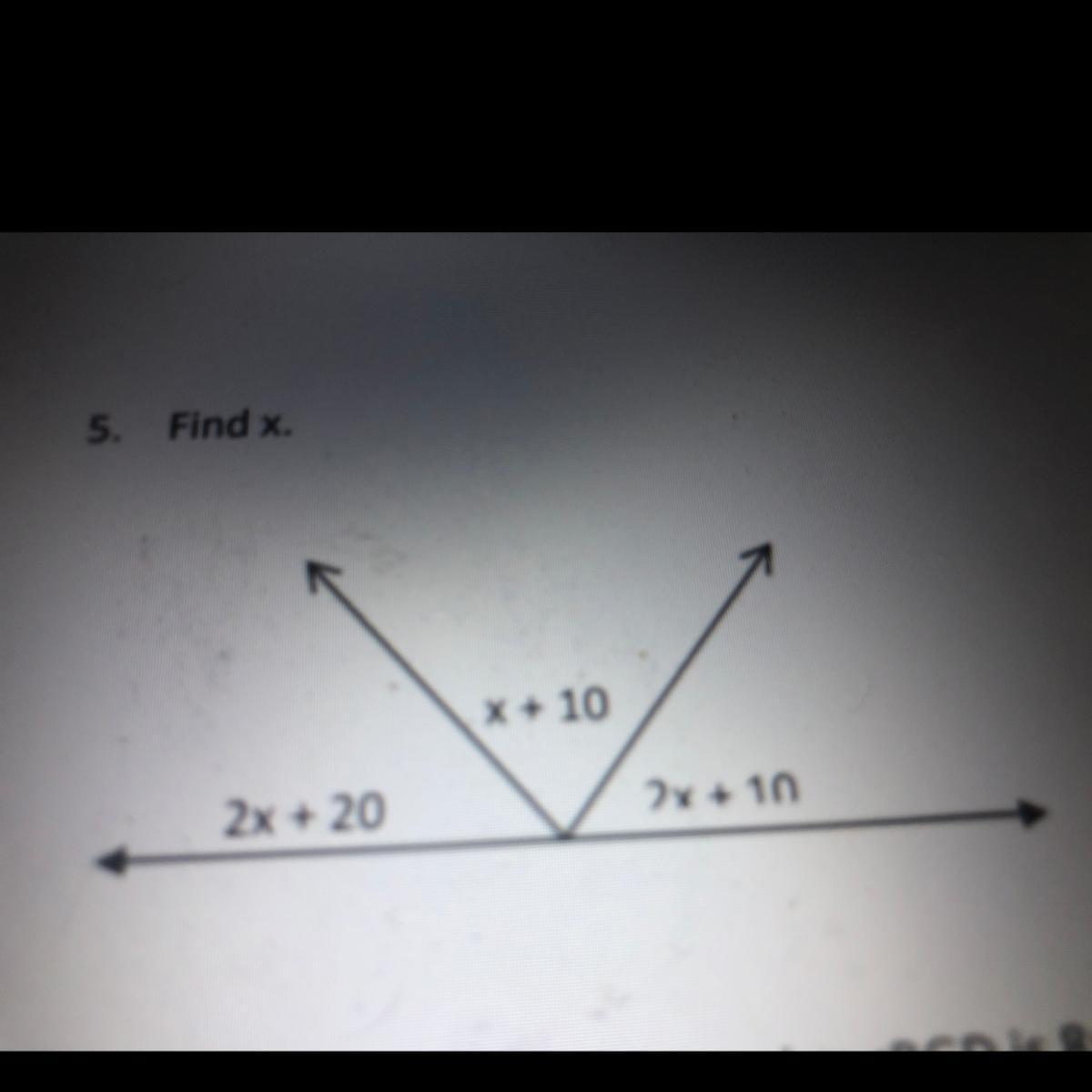
Answers
You then get 5x + 40 = 180
Subtract 40 from both side and then divide both side by 5.
You should get x = 28 degrees
Select two trigonometric functions that are equivalent to the ratio x/y.
Answers
Sine and cosine are both equivalent to x/y, depending on the angle of the point on the circle.
To find two trigonometric functions equivalent to the ratio x/y, we can use the unit circle. Let's assume that x and y are the coordinates of a point on the circle, where x represents the horizontal displacement, and y represents the vertical displacement.
From this, we can find that the sine of the angle that x and y make with the x-axis is y, and the cosine of that angle is x. Therefore, the two trigonometric functions equivalent to the ratio x/y are sine and cosine.
We can write this as sin(angle) = y/y and cos(angle) = x/y. It's important to note that the value of the angle depends on the position of the point on the unit circle.
So, sine and cosine are both equivalent to x/y, depending on the angle of the point on the circle.
To know more about trigonometry, refer here:
https://brainly.com/question/14272510#
#SPJ11
Find the Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) for the curve →r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0. Round answers to 3 decimal places.
T(0) =0=[sqrt(89)= sqrt(89)]
N(0) =[ ]
B(0) =[ ]
Answers
The tangent vector → \(r(t)=〈4cos(2t),4sin(2t),5t〉\), normal vector at t=0 is given by →N(0) = 〈-1,0,0〉, and binormal vector at t=0 is given by →\(B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector, normal vector, and binormal vector of the given curve are as follows:
Given curve:
→ \(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0
To find: Tangent vector, the Normal vector, and the Binormal vector (→T, →N and →B) at the point t=0
Tangent vector: To find the tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\) at the point t=0,
we need to differentiate the equation of the curve with respect to t.t = 0, we have:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉→r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
Differentiating w.r.t t:→\(r(t) = 〈4cos(2t),4sin(2t),5t〉 → r'(t) = 〈-8sin(2t),8cos(2t),5〉t = 0\),
we have:
→\(r'(0) = 〈-8sin(0),8cos(0),5〉= 〈0,8,5〉\)
Therefore, the tangent vector at t = 0 is given by
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Normal vector:To find the normal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to differentiate the equation of the tangent vector with respect to t.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating w.r.t t:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉t = 0\),
we have:
→\(T'(0) = 〈-16cos(0),-16sin(0),0〉= 〈-16,0,0〉\)
Therefore, the normal vector at t = 0 is given by
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Binormal vector: To find the binormal vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0, we need to cross-product the equation of the tangent vector and normal vector of the curve.t = 0, we have:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉\)
The cross product of two vectors:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the binormal vector at t = 0 is given by→B(0) = 〈0, -0.441, -0.898〉
Hence, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are as follows:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The given curve is
→\(r(t)=〈4cos(2t),4sin(2t),5t〉 at the point t=0.\)
We are asked to find the tangent vector, the normal vector, and the binormal vector of the given curve at t=0.
the tangent vector at t=0. To find the tangent vector, we need to differentiate the equation of the curve with respect to t. Then, we can substitute t=0 to find the tangent vector at that point. the equation of the curve Is:
→\(r(t) = 〈4cos(2t),4sin(2t),5t〉\)
At t = 0, we have:
→\(r(0) = 〈4cos(0),4sin(0),5(0)〉= 〈4,0,0〉\)
We can differentiate this equation with respect to t to get the tangent vector as:
→\(r'(t) = 〈-8sin(2t),8cos(2t),5〉\)
At t=0, the tangent vector is:
→\(T(0) = r'(0) / |r'(0)|= 〈0,8,5〉 / sqrt(89)≈〈0.000,0.898,0.441〉\)
Next, we find the normal vector. To find the normal vector, we need to differentiate the equation of the tangent vector with respect to t. Then, we can substitute t=0 to find the normal vector at that point.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
Differentiating this equation with respect to t, we get the normal vector as:
→\(T'(t) = 〈-16cos(2t),-16sin(2t),0〉\)
At t=0, the normal vector is:
→\(N(0) = T'(0) / |T'(0)|= 〈-16,0,0〉 / 16= 〈-1,0,0〉\)
Finally, we find the binormal vector. To find the binormal vector, we need to cross-product the equation of the tangent vector and the normal vector of the curve.
At t=0, we can cross product →T(0) and →N(0) to find the binormal vector.
At t=0, the tangent vector is:
→\(T(0) = 〈0.000,0.898,0.441〉\)
The normal vector is:
→N(0) = 〈-1,0,0〉Cross product of two vectors →T(0) and →N(0) is given as:
→\(B(0) = →T(0) × →N(0)= 〈0.000,0.898,0.441〉 × 〈-1,0,0〉= 〈0, -0.441, -0.898〉\)
Therefore, the tangent vector, normal vector, and binormal vector of the given curve at t=0 are:
→\(T(0) = 〈0.000,0.898,0.441〉→N(0) = 〈-1,0,0〉→B(0) = 〈0, -0.441, -0.898〉\)
The tangent vector of the given curve
→\(r(t)=〈4cos(2t),4sin(2t),5t〉\)
at the point t=0 is given by →\(T(0) = 〈0.000,0.898,0.441〉.\)
The normal vector at t=0 is given by →N(0) = 〈-1,0,0〉.
The binormal vector at t=0 is given by →B(0) = 〈0, -0.441, -0.898〉.
To know more about binormal vectors visit
brainly.com/question/31673319
#SPJ11
3gh^2 x 4g^3 h^3 what is the answer
Answers
Answer: 12, g with exponent 4, h with exponent 5 . (12
g
4
h
5
Brainliest would be much apprechiated
Answer:
2+3+3=8
3×4=12
Step-by-step explanation:
Question 4 (1 point ) Tell whether the sequence is arithmetic. If it is, what is the common difference? 2,7,13,20,dots
a yes; 5
b yes; 6 c yes; 2 d no
Answers
The sequence is arithmetic. The common difference is 6. Answer: b
If a sequence is arithmetic, there exists a common difference d that is added to each term to get the next term. For instance, given the sequence 2, 5, 8, 11, 14, ... to get each of the subsequent terms, we add 3. 2 + 3 = 5; 5 + 3 = 8, and so on.
The given sequence is 2,7,13,20, ...To determine whether it is an arithmetic sequence, we need to find the common difference d.
Subtract each subsequent term from its preceding term;7 - 2 = 513 - 7 = 620 - 13 = 7
Therefore, the common difference d is 6.
learn more about arithmetic here
https://brainly.com/question/6561461
#SPJ11
Question 9 of 10
Which pairs of angles in the figure below are vertical angles?
Check all that apply.

Answers
Answer:
B. ∠TRF and ∠NRLC. ∠LRE and ∠FRAStep-by-step explanation:
→ The lines TN and FL intersect each other
at the point R forming the opposite angles ∠TRF and ∠NRL
then
∠TRF and ∠NRL are verticals angles.
………………………………………………………………………
→ The lines LF and AE intersect each other
at the point R forming the opposite angles ∠LRE and ∠FRA
then
∠LRE and ∠FRA are verticals angles.
On the last day of the schoolbook fair, all pencils were one set price and all books were a different set price. Sammy
bought 2 pencils and 6 books for $14. Belle bought 4 pencils and 1 book for $8. What was the set price for a pencil?
What was the set price for a book?
Answers
Answer: wee wee woo woo peep pop doo doo
Step-by-step explanation:You have to be a cool kid to know answer
Answer: Ax+By=c
2x+6y=14
4x+1y=8
x=1.54
y=1.82
Step-by-step explanation:
Determine if the sequence {an} converges or diverges. Find the limit if the sequence converges. (-1)+1 an = 4n-3 Select the correct choice below and fill in any answer boxes within your choice. O A. The sequence {an} converges. The limit is lim an = (Simplify your answer.) n+00 B. The sequence {an} diverges.
Answers
The given sequence {an} = 4n - 3 does not converge. As n approaches infinity, the terms of the sequence continue to grow without bound. Therefore, the correct choice is: B. The sequence {an} diverges.
To determine if the sequence {an} = 4n - 3 converges or diverges, we can analyze the behavior of the sequence as n approaches infinity.
Step 1: Take the given expression for the nth term of the sequence, which is an = 4n - 3.
Step 2: Consider what happens to the terms of the sequence as n becomes larger and larger (approaching infinity).
Step 3: As n increases, the term 4n dominates the expression, while the constant term -3 becomes insignificant compared to the growing term.
Step 4: The sequence grows without bound as n approaches infinity because the term 4n increases indefinitely without any upper limit.
Step 5: Since the terms of the sequence do not approach a specific value or become bounded, we conclude that the sequence {an} diverges.
Therefore, the correct choice is:
B. The sequence {an} diverges.
learn more about "converge":- https://brainly.com/question/17019250
#SPJ11
Give the boundaries of the indicated value.
4 feet

Answers
The solution is, the boundaries of the indicated value,
4 feet is 16 ft.
What is perimeter?A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference. Calculating the perimeter has several practical applications.
Perimeter refers to the total outside length of an object,
here, we have,
the length = 4 ft.
so, boundary = perimeter of the square
i.e. 4+4+4+4
=4*4
=16
Hence, The solution is, the boundaries of the indicated value,
4 feet is 16 ft.
Learn more about perimeter here:
brainly.com/question/397857
#SPJ2
ezra determined that the graph shown below is vertically compressed by a factor of 1/3 from the graph of y=|x| do you agree or disagree? why?
Answers
Answer:
Step-by-step explanation:
no graph was shown
Lyon walked 3/4 mile from school to the soccer field.
He then walked 1/6 mile home.
About how many miles did Lyon walk?
Answers
Answer:
11/12 miles Lyon walk.
Step-by-step explanation:
3/4 -> 9/12
1/6 -> 2/12
9 + 2 = 11
The solution is :about 11/12 miles Lyon walk.
What is addition?Addition is a way of combining things and counting them together as one large group. ... Addition in math is a process of combining two or more numbers.
here, we have,
given that,
Lyon walked 3/4 mile from school to the soccer field.
He then walked 1/6 mile home.
now, we have to find that,
About how many miles did Lyon walk
so, we need to add the both distance
i.e. 3/4 + 1/6
so, we have,
3/4 -> 9/12
1/6 -> 2/12
so, we get,
9 + 2 = 11
i.e. 3/4 + 1/6
= 9/12 + 2/12
=11/12
Hence, about 11/12 miles Lyon walk.
To earn more on addition click:
brainly.com/question/29560851
#SPJ2
Why is scientific notation useful in economics?
Answers
Answer:
20:48
Introduction to scientific notation (video)
Step-by-step explanation:
you drop a ball off a 50 foot roof to see how long it will bounce. Each bounce loses 10% of the height of its previous bounce. How high will the 8th bounce be in feet?
Answers
The height of the 8th bounce will be approximately 32.805 feet.
To calculate the height of the 8th bounce, we need to consider the initial height and the decrease in height with each bounce.
Given:
Initial height = 50 feet
Each bounce loses 10% of the height of the previous bounce.
To calculate the height of each bounce, we can use the formula:
Height of each bounce = Initial height × (1 - Percentage decrease)
Since each bounce loses 10% (0.1) of the height of the previous bounce, the percentage decrease is 0.1.
Height of the 1st bounce = 50 feet × (1 - 0.1) = 50 feet × 0.9 = 45 feet
For the subsequent bounces, we can apply the same formula:
Height of the 2nd bounce = 45 feet × (1 - 0.1) = 45 feet × 0.9 = 40.5 feet
Height of the 3rd bounce = 40.5 feet × (1 - 0.1) = 40.5 feet × 0.9 = 36.45 feet
We can continue this process for each subsequent bounce. Let's calculate the height of the 8th bounce:
Height of the 8th bounce = Height of the 7th bounce × (1 - 0.1) = 36.45 feet × 0.9 = 32.805 feet
Therefore, the height of the 8th bounce will be approximately 32.805 feet.
For more such questions on height , Visit:
https://brainly.com/question/28122539
#SPJ11
a container with a square base, vertical sides, and closed top is to have a volume of 2000 cm 3 . it costs twice as much per square centimeter to make the top and bottom as it does the sides. find the dimensions of the container that will minimize the cost
Answers
Ans .: The dimensions of the container that will minimize the cost are a base with sides of length 16.7 cm and a height of 8.35 cm.
To minimize the cost of the container, we need to find the dimensions that will use the least amount of material. Let's call the length of one side of the square base "x" and the height of the container "h".
The volume of the container is given as 2000 cm^3, so we can write:
V = x^2h = 2000
We need to find the dimensions that will minimize the cost, which is determined by the amount of material used. We know that it costs twice as much per square centimeter to make the top and bottom as it does the sides.
Let's call the cost per square centimeter of the sides "c", so the cost per square centimeter of the top and bottom is "2c". The total cost of the container can then be expressed as:
Cost = 2c(x^2) + 4(2c)(xh)
The first term represents the cost of the top and bottom, which is twice as much as the cost of the sides. The second term represents the cost of the four sides.
To minimize the cost, we can take the derivative of the cost function with respect to "x" and set it equal to zero:
dCost/dx = 4cx + 8ch = 0
Solving for "h", we get:
h = -0.5x
Substituting this into the volume equation, we get:
x^2(-0.5x) = 2000
Simplifying, we get:
x^3 = -4000
Taking the cube root of both sides, we get:
x = -16.7
Since we can't have a negative length, we take the absolute value of x and get:
x = 16.7 cm
Substituting this into the equation for "h", we get:
h = -0.5(16.7) = -8.35
Again, we can't have a negative height, so we take the absolute value of "h" and get:
h = 8.35 cm
Therefore, the dimensions of the container that will minimize the cost are a base with sides of length 16.7 cm and a height of 8.35 cm.
Learn more about :
volume : brainly.com/question/28058531
#SPJ11
A football team has an away game, and the bus breaks down. The coaches decide to drive the players to the game in cars and vans. Four players can ride in each car. Six players can ride in each van. There are 48 players on the team. The equation $4x+6y=48$ models this situation, where $x$ is the number of cars and $y$ is the number of vans
Answers
The 4 possible solutions in the context of the problem are (0, 8), (3, 6), (6, 3), and (9, 2)
Given the equation that models the situation expressed as:
4x + 6y = 48
We are to find 4 possible solutions for x and y. Note that the values of x and y must be integers.
If there are no cars i.e. at when x = 0
4(0) + 6y = 48
0 + 6y = 48
6y = 48
y = 48/6
y = 8
One of the solution is (0, 8)
If there are 3 cars, i.e. at when x = 0
4(3) + 6y = 48
12 + 6y = 48
6y = 48 - 12
y = 36/6
y = 6
The second solution will be (3, 6)
If there are 6 cars, i.e. at when x = 6
4(6) + 6y = 48
24 + 6y = 48
6y = 48 - 24
y = 24/6
y = 4
The third solution will be (6, 3)
If there are 9 cars, i.e. at when x = 9
4(9) + 6y = 48
36 + 6y = 48
6y = 48 - 36
y = 12/6
y = 2
The fourth solution will be (9, 2)
Hence the 4 possible solutions in the context of the problem are (0, 8), (3, 6), (6, 3), and (9, 2)
Learn more about Probability here:
brainly.com/question/2159099
#SPJ9
The recommended daily intake of vitamin C for males 18 years and older is 90 milligrams. If an 18 year-old male has already consumed 36 milligrams of vitamin C, what percentage of the daily recommended amount has he already consumed?
Answers
Answer:
40%
Step-by-step explanation:
Jaida worked 21.5 hours last week. She earned $11.60 per hour of work.
How much money did Jaida earn last week?
$9.90
$249.40
$1.85
$33.10
Answers
Answer:
249.40 Option b
Step-by-step explanation:
When multiplying 21.5 x 11.60 you get $249.40
#6 write it in y=MX+B

Answers
Answer:
\(m = \frac{14 - 7}{2 - 0} = \frac{7}{2} \)
\(14 = \frac{7}{2} (2) + b\)
\(14 = 7 + b\)
\(b = 7\)
\(y = \frac{7}{2} x + 7\)
Liam is setting up folding chairs for a meeting. If he arranges the chairs in 9 rows of the same length, he has 5 chairs left over. If he arranges the chairs in 7 rows of that same length, he has 15 left over. How many chairs does Liam have?
Answers
Answer:
50 Chairs
Step-by-step explanation:
To solve this we can make two equations to represent each situation-
9x + 5 = 7x + 15
Now we cancel 7x from each side
9x + 5 - 7x = 7x + 15 - 7x
2x + 5 = 15
Now we cancel 5 from each side!
2x + 5 - 5 = 15 - 5
2x = 10, x = 5
So we plug in the value into the equations, and get:
50 chairs
Hope this helps!!
someone pls help am i on the verge of tears♀️

Answers
Answer:
trial 4 you got this!
Step-by-step explanation:
see how its 22 22 22 22 22 22 than it says 22-24
Select the correct answer. Transversal t cuts parallel lines r and s. Which angles must be congruent to ∠2? A. ∠3, ∠6, and ∠7 B. ∠7 only C. ∠7 and ∠6 D. ∠3, ∠5, and ∠6
Answers
Answer:
The correct answer is A. Which are angles 3, 6, and 7 I just took the test and got it correct.
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
Select the correct answer.
Rita is making a beaded bracelet. She has a collection of 160 blue beads, 80 gray beads, and 240 pink beads. What is the estimated probability that Rita will need to pick at least five beads before she picks a gray bead from her collection?
Use the table of randomly generated outcomes to answer the question. Each letter represents the first letter of the bead color.
Outcomes
PBBB GPBP PBPP GGGG BPBP GBPB GPBP GBPB
PBPP PPGP PBGG GPPB PPPG BPPP PPPG BPGP
GGGG PGPG PPPP PPPP BBBG PPGB BBBG PPGB
PBPB BPPG PBBG BPBB PGPP PBPP PPPP PBPP
PPBP PPBB PGBP BPPB PPPB PPPB PGGB BBBB
A.
0.05
B.
0.10
C.
0.45
D.
0.55
Answers
The estimated probability that Rita will need to pick at least five beads before she picks a gray bead from her collection is 0.45 which is denoted as option C.
What is Probability?
This is referred to as a number that indicates how likely the event is to occur.
Probability for drawing at least 5 beads before she picks a grey bead from her collection
= 1-Probability for drawing at least one grey bead in the first 5 draws.
No of grey beads drawn in first 5 trials = (5, 80/80+160+240)
= (5, 1/6)
Probability for drawing at least one grey bead in the first 5 draws.
=1 - Prob of no grey
Required probability = P(X=0 in first 5 draws) = (1/6)⁵ = 0.4018 and th nearest value is therefore 0.45.
Read more about Probability here https://brainly.com/question/25870256
#SPJ1
besides the 90° angle measure, what are the other two angle measures of a right triangle with side lengths 5, 12, and 13? round to the nearest degree. 18° and 39° 23° and 67° 43° and 47° 65° and 25°
Answers
The other two angle measures of a right triangle with side lengths 5, 12, and 13 can be found using trigonometric ratios. Let's label the sides of the triangle as follows:
- The side opposite the angle we are looking for is 5.
- The side adjacent to the angle we are looking for is 12.
- The hypotenuse is 13.
To find the first angle, we will use the inverse tangent function (tan^(-1)). The formula is:
Angle = tan^(-1)(opposite/adjacent)
Plugging in the values, we get:
Angle = tan^(-1)(5/12)
Using a calculator, we find this angle to be approximately 22.6 degrees (rounded to the nearest degree).
To find the second angle, we will use the fact that the sum of the angles in a triangle is 180 degrees. Therefore, the second angle can be found by subtracting the right angle (90 degrees) and the first angle from 180 degrees.
Second angle = 180 - 90 - 22.6
Calculating this, we find the second angle to be approximately 67.4 degrees (rounded to the nearest degree).
Therefore, the other two angle measures of the right triangle are approximately 23 degrees and 67 degrees.
To know more about angle visit
https://brainly.com/question/30147425
#SPJ11