for the system shown below what are the coordinates of the solution that lies in quadrant 1 x^2+4y^2=100 4y-x^2=-20
Answers
The coordinates of the solution that lies in quadrant 1 for the given system are (-2, -5).
To find the coordinates of the solution that lies in quadrant 1 for the given system of equations, x^2 + 4y^2 = 100 and 4y - x^2 = -20, we need to solve the equations simultaneously.
Rearranging the second equation, we have x^2 = 4y + 20. Substituting this value of x^2 into the first equation, we get 4y + 20 + 4y^2 = 100.
Combining like terms, we have 4y^2 + 4y - 80 = 0.
Dividing the equation by 4, we obtain y^2 + y - 20 = 0.
Factoring the quadratic equation, we have (y + 5)(y - 4) = 0.
Setting each factor equal to zero, we find y = -5 and y = 4.
Substituting these values of y back into the second equation, we can solve for x.
When y = -5, we get 4(-5) - x^2 = -20, which gives x = -2.
When y = 4, we get 4(4) - x^2 = -20, which has no real solutions.
Therefore, the solution that lies in quadrant 1 is (x, y) = (-2, -5).
Know more about coordinates here:
https://brainly.com/question/30227780
#SPJ8
Related Questions
A professor gives her 100 students an exam; scores are normally distributed. The section has an average exam score of 80 with a standard deviation of 6.5. What percentage of the class has an exam score of A- or higher (defined as at least 90)? Type your calculations along with your answer for full credit; round your final percentage to two decimal places.
Answers
Answer:
6.18% of the class has an exam score of A- or higher.
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 80, \sigma = 6.5\)
What percentage of the class has an exam score of A- or higher (defined as at least 90)?
This is 1 subtracted by the pvalue of Z when X = 90. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{90 - 80}{6.5}\)
\(Z = 1.54\)
\(Z = 1.54\) has a pvalue of 0.9382
1 - 0.9382 = 0.0618
6.18% of the class has an exam score of A- or higher.
what is 5 8/12 as a mixed number in simplest form
Answers
Answer:
= \(5\frac{2}{3}\)Step-by-step explanation:
5 Keisha needs postage stamps to mail
invitations for her birthday party to
9 friends. If stamps cost 45¢ each, how
much will it cost Keisha to mail the
invitations?
LA
$
Answers
Answer:
$4.05
Step-by-step explanation:
45 x 9 = 4.05
1. A new compact has a sticker price of $14500. Options add another $982. Destination charges are $592. Dealer preparation is 5% of the total price. Sales tax is 7%. Tag fee is $145. Title fee is $45. What is the total price of the vehicle?
2. The selling price of a used car is $8850. Trade in allowance is $1500. Tax is 8%. Tag fee is $130. Title fee is $35. Finance charges are 9.5% annual simple interest. What is the total price of the financed amount? What are the total finance charges? What are the monthly payments if the vehicle is financed for 3 years? What is the total deferred price of the car?
3. The total deferred price of a car is $28000. After a down payment of $2100, the monthly payments are $380. How long is the financing agreement?
4. Stanley bought a new car with a sticker price of $19200. The dealer agreed to a 6% discount. The sales tax was 8% of the selling price. The tag fee was $65, and the title fee was $45. What is the total price of the car? The interest rate is 9% for financing the car for 5 years. What is the total deferred price after all the payments were made?
5. Mark bought a truck with a sticker price of $23000 plus additional options totaling $3500. He received a 4% discount and a $1500 trade-in allowance. The tax was 7%, tag fee was $125, and title fee was $75. He bought an extended warranty for $700, which was financed into the total cost of the truck. The interest rate was 6.5% for 5 years. How much are the monthly payments?
Answers
The total price of the vehicle would be $18,192.88.
The total deferred price of the car would be $11,191.60.
The length of the financing agreement is 68 months .
The total deferred price after the payments was $19,601.84.
The monthly payments would be $516.92.
How to find the price of the vehicle ?Subtotal = Base price + Options + Destination charges
Subtotal = $14,500 + $982 + $592 = $16,074
Dealer preparation = 5% of subtotal
Dealer preparation = 0.05 x $16,074 = $803.70
Sales tax = 7% of subtotal
Sales tax = 0.07 x $16,074 = $1,125.18
Total price = Subtotal + Dealer preparation + Sales tax + Tag fee + Title fee
Total price = $16,074 + $803.70 + $1,125.18 + $145 + $45 = $18,192.88
How to find the total deferred price ?Tax = 8% of selling price = 0.08 x $8,850 = $708
Tag fee = $130
Title fee = $35
Total amount financed = Amount financed + Tax + Tag fee + Title fee = $7,350 + $708 + $130 + $35 = $8,223
Annual interest rate = 9.5%
Number of years financed = 3
Total finance charges = $8,223 x 0.095 x 3 = $2,341.595
Total financed amount = $8,223 + $2,341.595 = $10,564.595
Monthly payments = Total financed amount / (Number of years financed x 12 months) = $10,564.595 / (3 x 12) = $293.4615
Total deferred price = Selling price + Total finance charges = $8,850 + $2,341.595 = $11,191.595
How to find the length of the financing agreement ?Total deferred price = $28,000
Down payment = $2,100
Total amount financed = Total deferred price - Down payment = $28,000 - $2,100 = $25,900
Monthly payments = $380
Number of months = Total amount financed / Monthly payments = $25,900 / $380 = 68.16
The financing agreement is approximately 68 months long.
How to find the deferred price after the payments ?Sticker price = $19,200
Discount = 6% of sticker price = 0.06 x $19,200 = $1,152
Selling price = Sticker price - Discount = $19,200 - $1,152 = $18,048
Sales tax = 8% of selling price = 0.08 x $18,048 = $1,443.84
Total price = Selling price + Sales tax + Tag fee + Title fee = $18,048 + $1,443.84 + $65 + $45 = $19,601.84
How to find the monthly payments ?Using the formula for monthly payments on a loan:
P = (PV x r x (1 + r)^ n) / ((1 + r) ^ n - 1)
= ($26,515.80 x 0.005265 x (1 + 0.005265) ^ 60 ) / ((1 + 0.005265) ^ 60 - 1) = $516.92
Find out more on monthly payments at https://brainly.com/question/27926261
#SPJ1
What is the measure of XYZ?
Answers
Answer:
a. An inscribed angle is 1/2 the intercepted arc. The intercepted arc is 68°. The measure of angle xyz is therefore 34°.
Answer:
34 degrees
Step-by-step explanation:
Prove that the roots of x² + (1-k)x+k-3=0 are real for all real values of k.
Answers
Answer:
Step-by-step explanation:To prove that the roots of the equation x² + (1-k)x + k-3 = 0 are real for all real values of k, we need to show that the discriminant of the equation is non-negative for all values of k.
The discriminant of a quadratic equation ax² + bx + c = 0 is given by b² - 4ac. If the discriminant is positive, then the equation has two distinct real roots; if it is zero, then the equation has one real root (a repeated root); and if it is negative, then the equation has no real roots.
So, in this case, the discriminant of the equation is:
(1-k)² - 4(1)(k-3)
= 1 - 2k + k² - 4k + 12
= k² - 6k + 13
We need to show that k² - 6k + 13 ≥ 0 for all real values of k.
To do this, we can complete the square:
k² - 6k + 13
= (k - 3)² + 4
Since the square of any real number is non-negative, we have (k-3)² ≥ 0 for all k, which means that (k-3)² + 4 ≥ 4.
Therefore, k² - 6k + 13 ≥ 4 for all real values of k, which means that the discriminant of the quadratic equation x² + (1-k)x + k-3 = 0 is non-negative for all real values of k. Hence, the roots of the equation are real for all real values of k.
For the quadratic equation x² + (1-k)x+k-3=0, we have:
a = 1
b = 1-k
c = k-3
Using the quadratic formula, we can find the roots of the equation:
x = (-b ± sqrt(b²-4ac))/2a
Substituting in the values of a, b, and c, we get:
x = (-(1-k) ± sqrt((1-k)² - 4(1)(k-3)))/2(1)
Simplifying, we get:
x = (k-1 ± sqrt((k-1)² - 4(k-3)))/2
Expanding the square inside the square root, we get:
x = (k-1 ± sqrt(k² - 2k + 1 - 4k + 12))/2
Simplifying further, we get:
x = (k-1 ± sqrt(k² - 2k + 13))/2
In order for the roots to be real, the expression inside the square root must be non-negative. That is:
k² - 2k + 13 ≥ 0
To find the values of k that satisfy this inequality, we can use the quadratic formula again:
k = (2 ± sqrt(4 - 4(1)(13)))/2
k = 1 ± sqrt(-44)/2
Since the square root of a negative number is not a real number, there are no real values of k that satisfy this inequality. Therefore, the roots of x² + (1-k)x+k-3=0 are real for all real values of k.
For each of the 6 coverage areas of a standard homeowners insurance policy, briefly describe what they cover: Dwelling, Other Structures. Personal Property,
Loss of Use, Personal Liability, Medical Payments
Answers
Read more about homeowners insurance
brainly.com/question/30179892
#SPJ1
What’s the correct answer for this?
Answers
Answer:
C
Step-by-step explanation:
The fraction of girls among the members that play sports is equal to the fraction of boys among the members that do not play sports.
Answer:
Your correct answer is option C. which is The fraction of girls among the members that play sports is equal to the fraction of boys among the members that do not play sports.
Use the Distributive Property to correctly rewrite or simplify the expression:
21k+13k+9k
Answers
Answer:
21k+9k+13, and simplified into 43k.
Step-by-step explanation:
The distributive property means that you can put addends or factors in any order to get the same result(9+1=10, 1+9=10)
21k+13k+9k can be re-written into 21k+9k+13, and simplified into 43k.
Answer:
43k
Step-by-step explanation:
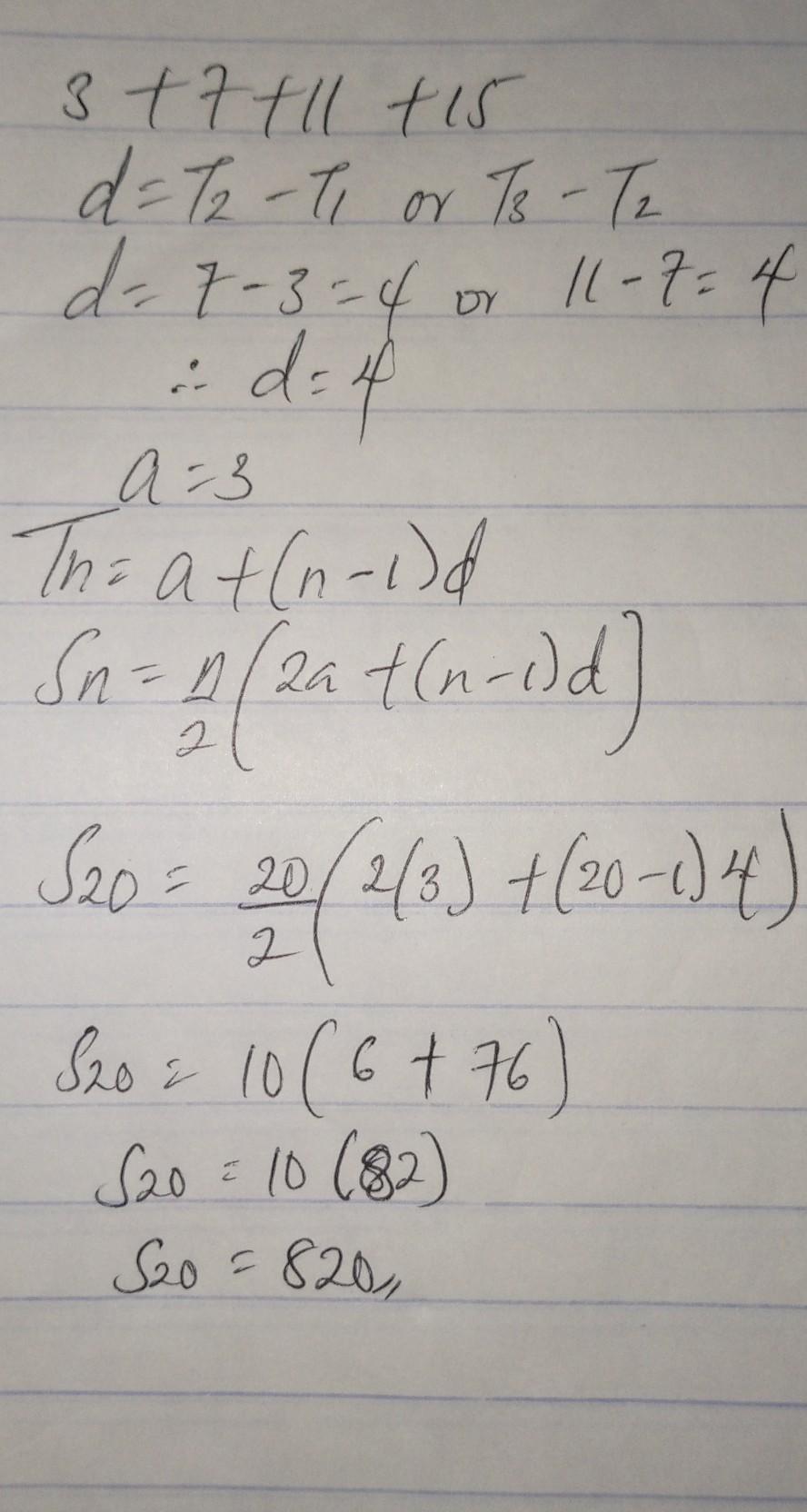
Los 1600 euros de alquiler de un terreno se reparten entre tres ganaderos que llevan alli a pastar sus ovejas. Como no tienen el mismo número de ovejas, deciden pagar proporcionalmente al número de ovejas de cada uno. Si el primero tiene 120 Ovejas,el segundo 72 y el tercero 68. ¿ Cuánto paga cada uno?
Answers
So, each farmer pays the following amounts: The first farmer pays 738.40 euros. The second farmer pays 443.04 euros. The third farmer pays 418.56 euros
What is proportion?Proportion refers to the equality of two ratios. In other words, when two ratios are set equal to each other, they form a proportion. A proportion is typically written in the form of two fractions separated by an equals sign, such as a/b = c/d. Proportions are commonly used in mathematics to solve problems involving ratios and proportions, such as finding missing values or scaling up or down a given quantity.
Here,
To find out how much each farmer pays, we need to determine the proportion of the total rent that each farmer owes based on the number of sheep they have. First, we need to find the total number of sheep:
120 + 72 + 68 = 260
The first farmer has 120 sheep, which is 46.15% of the total number of sheep (120/260). Therefore, the first farmer owes 46.15% of the rent:
0.4615 x 1600 = 738.40 euros
Similarly, the second farmer has 72 sheep, which is 27.69% of the total number of sheep (72/260). Therefore, the second farmer owes 27.69% of the rent:
0.2769 x 1600 = 443.04 euros
The third farmer has 68 sheep, which is 26.15% of the total number of sheep (68/260). Therefore, the third farmer owes 26.15% of the rent:
0.2615 x 1600 = 418.56 euros
To know more about proportion,
https://brainly.com/question/29474065
#SPJ1
Complete question:
The rent of 1600 euros for a piece of land is divided among three farmers who graze their sheep there. As they do not have the same number of sheep, they decide to pay proportionally according to the number of sheep each has. If the first one has 120 sheep, the second 72, and the third 68. How much does each one pay?
Find a vector equation with parameter t for the line of intersection of the planes x + y + z = 6 and x + z = 0
Answer r(t): ?
Answers
The vector equation with parameter t for the line of intersection along the planes is r(t) = < x(t), y(t), z > = < -t, 6 + t, t >
What is the vector equation with parameter t for the line of intersection of the planesTo find a vector equation with parameter t for the line of intersection of the planes x + y + z = 6 and x + z = 0, we can follow these steps:
1. Solve for one variable in terms of the other variables in each equation.
From the second plane equation, we have:
x + z = 0
x = -z
From the first plane equation, we can solve for y in terms of x and z:
y = 6 - x - z
Substituting the expression for x from the second equation into the first equation, we get:
y = 6 + z
2. Use these expressions for x, y, and z to form a vector equation with parameter t.
Let's choose z as the parameter t, so that our vector equation becomes:
r(t) = < x(t), y(t), z > = < -t, 6 + t, t >
This is a vector equation with parameter t for the line of intersection of the planes x + y + z = 6 and x + z = 0.
Learn more on vector here;
https://brainly.com/question/3184914
#SPJ1
ok, whats 23÷3 (45+4)?
Answers
Step-by-step explanation:
given
23÷3(45+4)
23÷3(49)
23/147
Answer:
41.4 I believe
Step-by-step explanation:
First we start in the () so we do 45+4= 49.
Next we divide 23 by 3 and we get 7.66666667, but we reduce that to 7.6.
Then we have 7.6 I don't know the sign we have to use, I used subtraction, so we do 7.6 - 49, which actually gives us -41.4,
Let me know if you have any questions. I couldn't do this 100% because I didn't know the choices but try this and if not, I apologize.
PLEASE I NEED HELP IN THIS
HERE IS THE PICTURE IS JUST ONE QUESTION
Answers
Answer:
f(x) = -5/9x - 11/9
Step-by-step explanation:
Consider f(x) = y
so if x = -4 => y = 1 and x = 5 => y = -4
so (-4,1) and (5,-4) should be on the same linear equation
Slope m = (y2 - y1)/(x2 - x1)
m = (-4 - 1)/(5 - -4) = (-5)/(9) = -5/9
y = mx + b
given m = -5/9, x = -4, y = 1
1 = -5/9(-4) + b
b = 1 - 20/9
b = 9/9 - 20/9 = -11/9
so y = -5/9x - 11/9
or f(x) = -5/9x - 11/9
help. use the figure shown to the right to find the value of x
Answers
Answer:
\(\begin{aligned}x &= 16\sqrt3 \\ &\approx 27.7\end{aligned}\)
Step-by-step explanation:
We can see that the longer leg (a) of a right triangle is half of the circle's radius. Since we are given the other two sides of the triangle (shorter leg and hypotenuse), we can solve for the length of the longer leg using the Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
↓ plugging in the given values
\(a^2 + 2^2 = 14^2\)
↓ subtracting 2² from both sides
\(a^2 = 14^2 - 2^2\)
\(a^2 = 196 - 4\)
\(a^2 = 192\)
↓ taking the square root of both sides
\(a = \sqrt{192\)
↓ simplifying the square root
\(a = \sqrt{2^6 \cdot 3\)
\(a = 2^{\, 6 / 2} \cdot \sqrt3\)
\(a = 2^3\sqrt3\)
\(a = 8\sqrt3\)
Now, we can solve for the radius (x) using the fact that the longer leg of the triangle is half of it.
\(a = \dfrac{1}{2}x\)
↓ plugging in the a-value we solved for
\(8\sqrt3 = \dfrac{1}2x\)
↓ multiplying both sides by 2
\(\boxed{x = 16\sqrt3}\)
Help help help help help help please
Answers
Answer:
566
Step-by-step explanation:
i hope its right
for each parallel lines. you are given the measure of one angle
Answers
Answer:
The question is not complete
How do i write the prime factorization of 360 using division by primes?
Answers
3602=180
please help meeee!!!!!
Answers
Answer:
The answer is option 1
Answer:
Option 1
Step-by-step explanation:
What is the power of A if 5a=1/125
Answers
Answer:
5^a= 1/5^3
5^a= 5^-3
a=-3
Step-by-step explanation:
anyone have the answer?
Answers
Answer:
50.3 (rounded) I think? Could be wrong, however, it's what I got
MATH 144 : College Math
Answers
Miguel will need to deposit approximately $3,261.25 into the annuity each year for 8 years in order for the annuity to have a total value of $24,000.
What is the annuity?
An annuity is a contract between you and an insurance company that requires the insurer to make payments to you, either immediately or in the future. You buy an annuity by making either a single payment or a series of payments.
We can use the formula for the future value of an annuity:
FV = PMT * \(((1 + r)^n - 1) / r\)
where FV is the future value, PMT is the regular payment, r is the interest rate per compounding period, and n is the number of compounding periods.
In this problem, we want to solve for PMT, given that FV = $24,000, r = 6.6%, n = 8, and payments are made at the end of each year.
First, we need to calculate the interest rate per year, since the annuity is compounded annually:
i = r / 100 = 6.6% / 100 = 0.066
Next, we can plug in the values and solve for PMT:
24000 = PMT *\(((1 + 0.066)^8 - 1) / 0.066\)
24000 = PMT * 7.3605
PMT = 24000 / 7.3605
PMT ≈ $3,261.25
Hence, Miguel will need to deposit approximately $3,261.25 into the annuity each year for 8 years in order for the annuity to have a total value of $24,000.
To learn more about annuity, Visit
https://brainly.com/question/25792915
#SPJ1
Given 3 + 7 + 11 + 15 + … find S20
Answers
Answer:
Hi
Please mark brainliest ❣️
help with this it is so hard
Answers
Answer:
its 4.8
Step-by-step explanation:
i divided 7.5 by 12.5 and got 0.6 and added 4.2 and got 4.8
Answer:
here is your answerrrrrrrrrrr
Consider parallelogram QRST below. Use the information given in the figure to find m
Answers
The missing values are
<UTQ = 41 degree
x= 1
<UQT = 47 degree
We have a parallelogram QRST.
We know that the opposite sides of the parallelogram is equal and parallel then
QR || ST
QT || SR
Then, <SRT = <RTQ (<UTQ) (alternate Interior Angle)
<UTQ = 41
Similarly, <UQT = <SRQ = 47
Now, RU = UT
2x + 1= 3
2x = 2
x= 1
Learn more about Parallelogram here:
https://brainly.com/question/32033686
#SPJ1
Anyone good at math I will pay $10 a test for someone to take my tests in mymathlab Mathlab also lets you pause the test and go look at the problems for help and you can take as much time as you need also you get three attempts per test I'm not good at math so need help anyway message me if your interested 7274304792 someone please help me !! I will venmo you money
Answers
Deon bought a desktop computer and a laptop computer. Before finance charges, the laptop cost $300 more than the desktop. He paid for the computers using two different financing plans. For the desktop the interest rate was 6% per year, and for the laptop it was 7% per year. The total finance charges for one year were $398. How much did each computer cost before finance charges?
Answers
Answer:
i think
Desktop: $2900.00, Laptop: $3200.00
Step-by-step explanation:
A basketball player is 6 feet tall. His infant son is as tall. How tall is his son? (1 point)
A 1² ft.
B 2/² ft.
C 1 ft.
D 2 1/2 ft.
Answers
how to round 11,295 to the nearest ten thousand?
Answers
The area of a square is 81cm2.Find the length and perimeter.
Answers
Answer:
Step-by-step explanation:area= s*s
so~ the side will be 9 as 9*9=81
n the perimeter = 4*9= 36
The length is 9 cm
The perimeter is 36 cm.
please see the attached picture for full solution
Hope it helps
Good luck on your assignment.
Write your answer in a + bi form.
A=___
B=___
Answers
Answer:
Step-by-step explanation:
\(\frac{-3+7i}{-6-7i} \times \frac{-6+7i}{-6+7i} =\frac{18-21i-42i-49i^2}{(-6)^2-(7i)^2} \\=\frac{18-63i -49(-1)}{36-49i^2} \\=\frac{18+49-63 i}{36-49(-1)} \\=\frac{67-63i}{36+49} \\=\frac{67-63i}{85} \\=\frac{67}{85} +(\frac{-63}{85} )i\\\)
\(a=\frac{67}{85} \\b=\frac{-63}{85}\)