From the definition of the definite integral, we have lim _n →[infinity]3/n∑_k=1^n(6 k/n+sin(6 k π/n))=
Answers
From the definition of the definite integral, \(lim_{n\to\infty} \dfrac{3}{n}\sum_{k=1}^n(\dfrac{6k}{n}+sin(\dfrac{6k\Pi}{n}))\) is equivalent to \(\int_0^3(2x+sin(2\Pi x))dx\).
The definite integral is an elementary concept in calculus that represents the accumulated area between the graph of a function and the x-axis over a specific interval.
The given expression is \(lim_{n\to\infty} \dfrac{3}{n}\sum_{k=1}^n(\dfrac{6k}{n}+sin(\dfrac{6k\Pi}{n}))\) ...(1)
It is known that
\(\int_a^bf(x)dx = lim_{n\to \infty} \Delta x \sum_{i=1}^n f(x_i)\) ...(2)
where, \(\Delta x = \dfrac{b-a}{n}\)
Comparing equations (1) and (2),
\(\Delta x = \dfrac{3}{n}\) ...(3)
and
\(f(x_i) = \dfrac{6k}{n}+sin(\dfrac{6k\Pi}{n})\)...(4)
Take equation (3),
\(\Delta x = \dfrac{3}{n}\\\dfrac{b-a}{n} = \dfrac{3-0}{n}\)
a = 0 and b = 3.
Also, it is known that
\(x_i = a+k\Delta x\)
\(= 0+k\dfrac{3}{n}\\=\dfrac{3k}{n}\)
So, from above and equation (4), it can be concluded that:
\(f(\dfrac{3k}{n}) = \dfrac{6k}{n}+sin(\dfrac{6k\Pi}{n})\\f(\dfrac{3k}{n}) = 2\dfrac{3k}{n}+sin(2\Pi\dfrac{3k}{n})\)
Replace \(\dfrac{3k}{n}\) by x in the above equation:
\(f(x) = 2x+sin\ x\)
a, b, and f(x) have been obtained. Now, the definite integral can also be obtained.
Substitute for a,b, and f(x) in the left-hand side of equation (2) to get the definite integral as follows:
\(\int_0^3 (2x+sin\ x)dx\)
Thus, the given expression is equivalent to the definite integral \(\int_0^3 (2x+sin\ x)dx\).
Learn more about Definite Integral here:
https://brainly.com/question/29685762
#SPJ12
Related Questions
Can you help me solve this!

Answers
Hello!
surface area
= 2(6*2) + 2(4*2) + 4*6
= 2*12 + 2*8 + 24
= 24 + 16 + 24
= 64 square inches
Henry received 12 candies for performing well for his recent examinations. He shared 5 candies with his brother. What fraction of the original number of candies had he left? Leave your answer in the simplest form.
Answers
Answer: 7/12
Step-by-step explanation:
12/12-5/12=7/12
I need help pls!
A statue is 7 feet tall. How many inches tall is the statue? 1. foot = 12 inches
2
A. 62.5 inches
B.90 inches
C 75 inches
D.45 inches
Answers
Answer:
Step-by-step explanation:
7 feet 1 foot is 12 inches
7*12= 84 inches.
None of the choices are correct.
90 inches is 7.5 feet
62.5 inches is 5.2 feet
75 inches is 6.25 feet
Find the percent of the total area under the standard normal curve between the following z-scores. z=−1.5 and z=−0.7 The percent of the total area between z=−1.5 and z=−0.7 is %. (Round to the nearest integer.)
Answers
The percent of the total area under the standard normal curve between z = -1.5 and z = -0.7 is 18%.
To find the percent of the total area between two z-scores, we need to calculate the area under the standard normal curve between those two z-scores.
Using a standard normal distribution table or a statistical software, we can find the area to the left of each z-score and subtract the smaller area from the larger area to find the area between the z-scores.
For z = -1.5, the area to the left of z = -1.5 is approximately 0.0668.
For z = -0.7, the area to the left of z = -0.7 is approximately 0.2420.
The area between z = -1.5 and z = -0.7 is:
Area between z = -1.5 and z = -0.7 = Area to the left of z = -0.7 - Area to the left of z = -1.5
= 0.2420 - 0.0668
= 0.1752
To convert this area to a percentage, we multiply by 100:
Percentage of the total area between z = -1.5 and z = -0.7 = 0.1752 * 100 ≈ 17.52%
Rounding to the nearest integer, the percent of the total area between z = -1.5 and z = -0.7 is 18%.
The percent of the total area under the standard normal curve between z = -1.5 and z = -0.7 is approximately 18%.
To know more about percent , visit;
https://brainly.com/question/31323953
#SPJ11
Kelly subtracts 60° from 90° to find the measure of a missing
angle in an angle pair. What type of angle pair is she working
with?
Answers
Answer:
acute
Step-by-step explanation:
Answer:
Complementary angle pair is here working
Hope you satisfyedSolve the given differential equation:
xy''+y'=0
usually if it was the form (x^2)y''+xy'+5y=0, you could then assume (r^2)+(1-1)r+5=0
how do i start/solve this?
Answers
The solution to the given differential equation is \(y = a_0x^{[0]} + a_1x^{[1]} + a_2x^{[2]}\), where a_0, a_1, and a_2 are constants.
How to solve the differential equationTo fathom the given differential equation, xy'' + y' = 0, we will begin by expecting a control arrangement of the frame y = ∑(n=0 to ∞) a_nx^n, where a_n speaks to the coefficients to be decided.
Separating y with regard to x, we get:
\(y' = ∑(n=0 to ∞) a_n(nx^[(n-1))] = ∑(n=0 to ∞) na_nx^[(n-1)]\)
Separating y' with regard to x, we get:
\(y'' = ∑(n=0 to ∞) n(n-1)a_nx^[(n-2)]\)
Presently, we substitute these expressions for y and its subsidiaries into the differential condition:
\(x(∑(n=0 to ∞) n(n-1)a_nx^[(n-2))] + (∑(n=0 to ∞) na_nx^[(n-1))] =\)
After improving terms, we have:
\(∑(n=0 to ∞) n(n-1)a_nx^[(n-1)] + ∑(n=0 to ∞) na_nx^[n] =\)
Another, we compare the coefficients of like powers of x to zero, coming about in a boundless arrangement of conditions:
For n = 0: + a_0 = (condition 1)
For n = 1: + a_1 = (condition 2)
For n ≥ 2: n(n-1)a_n + na_n = (condition 3)
Disentangling condition 3, we have:
\(n^[2a]_n - n(a_n) =\)
n(n-1)a_n - na_n =
n(n-1 - 1)a_n =
(n(n-2)a_n) =
From equation 1, a_0 = 0, and from equation 2, a_1 = 0.
For n ≥ 2, we have two conceivable outcomes:
n(n-2) = 0, which gives n = or n = 2.
a_n = (minor arrangement)
So, the solution to the given differential equation is \(y = a_0x^{[0]} + a_1x^{[1]} + a_2x^{[2]}\), where a_0, a_1, and a_2 are constants.
Learn more about differential equations here:
https://brainly.com/question/28099315
#SPJ1
PLZ ANSWER! ONLY IF YOU ARE CORRECT! don’t answer if you don’t know please.

Answers
Answer:
10-
Step-by-step explanation:
Open the following image :)
ASAP!!!

Answers
what is the common denominator of 892.5 and 87.5 and 4200 and 396.25 and 5440
Answers
The most common denominator of 892.5, 87.5, 4200, 396.25, and 5440 is 1000.
Least Common Denominator(LCD):
When two or more fractions have the same denominator, they are called common divisors. The least common divisor (LCD) is the smallest number that is a common divisor of a given set of fractions. For addition and subtraction of fractions and for comparing two or more fractions, the given fractions must have a common denominator.
Given by the question.
To Find: the common denominator of these numbers; we have to represent them all as fractions with a common denominator.
First, we notice that 892.5 and 87.5 both have a denominator of 10. We can convert them to fractions with a denominator of 1000 as follows:
892.5 = 892.5/10 = 89.25/1000
87.5 = 87.5/10 = 8.75/1000
Next, we notice that 4200 and 5440 are both multiples of 10. We can convert them to fractions with a denominator of 1000 as follows:
4200 = 4200/10 = 420/100 = 42/10 = 42/1000
5440 = 5440/10 = 544/100 = 54.4/10 = 544/1000
Finally, 396.25 can be expressed directly as a fraction with a denominator of 1000:
396.25 = 396.25/1 = 39625/1000
Now that we have represented all numbers as fractions with a denominator of 1000, we can find their common denominator, which is 1000, by finding the least common multiple (LCM) of their denominators.
Learn more about Denominator:
https://brainly.com/question/7067665
#SPJ4
Follow the steps to finish solving the equation -3x + 18 = 7x
1. Add 3x to both sides to isolate the variable term.
2. Divide both sides by 10.
Xa
Answers
Answer:
Don’t really know what the question is, but these are the answers for x

use logarithmic differentiation to find the derivative of y = 3 √x(x −2) x2 1 . leave your answer unsimplified.
Answers
\(dy/dx = x(1 + ln x) (x - 2)^2 / 2\)
\(y = 3√x(x − 2) * x^2 * (1 + ln(x))\)
To find the derivative of y using logarithmic differentiation.
The formula to be used is given below,
\(dy/dx = y * (ln(dy/dx))\) ........(1)
Take natural logarithms of both sides of the given equation to get the following equation,
\(ln(y) = ln(3√x(x − 2)) + ln(x^2) + ln(1 + ln(x))\)
Differentiate with respect to x on both sides of the above equation and simplify,
\(1/y * dy/dx = 1/3√x(x − 2) * 3/2 (x-2) * (1/x) + 2/x + 1/x (1/1 + ln(x))\)
\(dy/dx = y * (1/y * dy/dx)\)
\(dy/dx = 3√x(x − 2) * x^2 * (1 + ln(x)) * (1/3√x(x − 2) * 3/2 (x-2) * (1/x) + 2/x + 1/x (1/1 + ln(x)))\)
Thus, \(dy/dx = x(1 + ln x) (x - 2)^2 / 2\)
To know more about derivative refer here:
https://brainly.com/question/29144258#
#SPJ11
The time it takes for YOU to read this question is a __________ random variable; the number of marshmallows YOU can fit into your mouth is a __________ random variable.
Answers
The time it takes to read this question is a continuous random variable; the number of marshmallows that can fit into your mouth is a discrete random variable.
The time it takes for an individual to read a question can be considered as a continuous random variable. It is typically measured on a continuous scale and can take on any value within a given range. For example, it may take someone 10 seconds to read a question, while it might take another person 20 seconds. The time it takes to read a question can vary continuously.
On the other hand, the number of marshmallows that a person can fit into their mouth can be considered as a discrete random variable. It is measured on a discrete scale and can only take on whole number values. For instance, a person may be able to fit 2, 3, or 4 marshmallows into their mouth, but they cannot fit a fractional or continuous number of marshmallows. The number of marshmallows is limited to specific integer values, making it a discrete random variable.
for such more question on random variable
https://brainly.com/question/16730693
#SPJ11
Can anyone help me with this problem I really need help! ⚠️⚠️⚠️
- Compare the dimensions of the prisims. How many time greather is the surface area of the red prism than the surface area of the blue prism
- fill in the blanks.

Answers
Answer:
The answer for the first one is 3 times
the answer for the second one is 9
Step-by-step explanation:
A rectangle has a height of x+ 9 and a width of x^2 + 2x
Express the area of the entire rectangle.
Your answer should be a polynomial in standard form.
X^2
+
2x
X
+
9
Answers
Answer:
x³ + 11x² + 18x
Step-by-step explanation:
(x² + 2x)(x + 9)
Step 1: Distribute x²+2x into x + 9.
x³ + 2x² + 9x² + 18x
Step 2: Combine like terms.
x³ + 11x² + 18x
The area of this rectangle is x³ + 11x² + 18x.
Answer:
Area= height x width = (x + 9) (x^2 + 2x) = x^3 + 2x^2 + 9x^2 + 18x = x^3 + 11 x^2 + 18x
Step-by-step explanation:
The height is (x + 9) and the width is (x^2 + 2x) and the the area of the rectangle is equal to: Area= height x width = (x + 9) (x^2 + 2x) = x^3 + 2x^2 + 9x^2 + 18x = x^3 + 11 x^2 + 18x
factorise the following expressions;
1. 8x + 6 2. 4x + 2
Answers
Answer:
Step-by-step explanation:
1. 8x + 6
2(4x+3)
2.4x+2
2(2x +1)
Answer:
\(\huge\boxed{\boxed{\underline{\textsf{\textbf{Answer}}}}}\)
1. \(\boxed{Factorise \ = \ 8x + 6}\)
⎆To factorise this, you have to take the common factor out. In this case, it's 2.
\(8x + 6 \\ = 2(4x + 3)\)
\(\boxed{Answer \ = \ 2(4x + 3)}\)
2) \(\boxed{Factorise \ = \ 4x + 2}\)
⎆To factorise this, you have to take the common factor out. In this case also, it's 2.
\(4x + 2 \\ = 2(2x + 1)\)
\(\boxed{Answer \ = \ 2(2x + 1)}\)
____________________
ʰᵒᵖᵉ ⁱᵗ ʰᵉˡᵖˢ
ღ \(RainbowSalt2^{2}2^{2} \)
1 2/3 x 1/3 =
This problem is so confusing to me I’m so lost on it can u help me
Answers
Answer: (If you are multiplying 1 2/3 by 1/3 this is for you.)
The simplest answer is 5/9.
Step-by-step explanation: First, turn the mixed number into an improper fraction. Ex: 1 2/3 --> 5/3 (The easiest way is to multiply your whole number by the denominator and add you answer to the numerator.
Ex: 1 x 3 (three is the denominator, one is the whole number.) Then add you answer to the numerator.
Ex: 3 is the answer for the multiplication step, 2 is the denominator. You sum is 5. Rewrite that as a fraction over the original denominator. You should get 5/3. Then last multiply your 2 fractions, 5/3 x 1/3 = 5/9.
find area of shape below to 1 dp

Answers
The shape will have a surface area of 189.25 cm². There are two distinct pieces to the figure: a rectangle and a semicircle.
What is the area?The space filled by a flat form or the surface of an item is known as the area.
The number of unit squares that cover the surface of a closed-form is the figure's area. Square centimeters and other similar units are used to measure area.
The figure is divided into two parts one is a rectangle and the second is a semicircle.
Area of figure = Area of rectangle + Area of a semicircle
Area of figure = L × B + (πr²/2)
A = 10 cm × 15 cm + (3.14 ×(5)^2/2)
A= 189.25 cm²
Hence the area of the shape will be 189.25 cm²
To learn more about the area, refer to the link;
https://brainly.com/question/11952845
#SPJ1
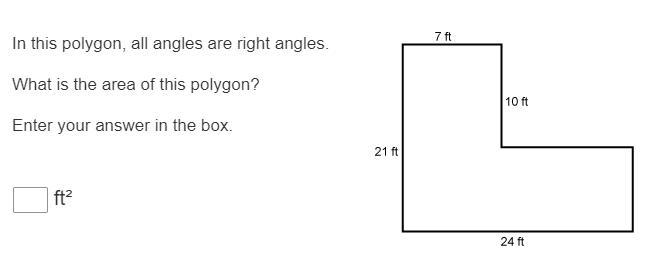
In this polygon all angles are right angles
What is the area of this polygon
Enter your answer in the box
Answers
Answer: 334
Step-by-step explanation:
Cut the polygon into 2 pieces
Find the area of each rectangle and some it
7*10 = 70
24*(21-10) = 264
264 + 70 = 334
Answer:
334 ft²
Step-by-step explanation:
split the polygon into two
Area of A = 21 ft × 7 ft = 147 ft²
Area of B = (21 ft - 10 ft) × (24 ft - 7 ft)
Area of B = 11 ft × 17 ft = 187 ft²
Area of polygon = sum of Areas of A and B
147 ft² + 187 ft² = 334 ft²

The sine of the complimentary angle to 75 degrees

Answers
Answer: 0.65
Step-by-step explanation:
Two angles are said to be complementary angles when the sun of their angles will be equal to 90°. In this case, since the angle given is 75°, then the other angle will be:
= 90° - 75°
= 15°
Therefore, we'll then find the sine of 15° which will be:
= Sine 15°
= 0.65
Therefore, the correct option is A.
9. Calculate the area of triangle \( A B C \) with \( A=20^{\circ}, b=13 \) inches and \( c=7 \) inches and round off your answer to the nearest whole number. Write down the work leading to your answe
Answers
The area of triangle ABC, given that angle A is 20 degrees, side b is 13 inches, and side c is 7 inches, is approximately 42 square inches (rounded to the nearest whole number).
To find the area of triangle ABC, we can use the formula:
Area = (1/2) * b * c * sin(A),
where A is the measure of angle A,
b is the length of side b,
c is the length of side c,
and sin(A) is the sine of angle A.
Given that A = 20 degrees, b = 13 inches, and c = 7 inches, we can substitute these values into the formula to calculate the area:
Area = (1/2) * 13 * 7 * sin(20)= 41.53≈42 square inches.
To learn more about triangle visit:
brainly.com/question/2773823
#SPJ11
Suppose a particle moves back and forth along a straight line with velocity v(t), measured in feet per second, and acceleration a(t). a) What is the meaning of 120 â« v(t) dt? 60 b) What is the meaning of 120 â« |v(t)| dt? 60 c) What is the meaning of 120 â« a(t) dt? 60
Answers
In this case, the displacement of the particle at time t is given by ∫ v(t) dt, and the displacement after 120 seconds is given by ∫_0^120 v(t) dt.
The integral of |v(t)| over the time interval [0, 120] gives the total distance traveled by the particle during that time.
Specifically, the value of the integral gives us the difference between the velocity of the particle at time t=120 and its velocity at time t=0.
a) The integral 120 ∫ v(t) dt represents the displacement of the particle from its starting point after 120 seconds, assuming that its initial displacement is zero. This can be seen by the fundamental theorem of calculus, which states that if F(x) is an antiderivative of f(x), then ∫ f(x) dx = F(b) - F(a), where a and b are the limits of integration. In this case, the displacement of the particle at time t is given by ∫ v(t) dt, and the displacement after 120 seconds is given by ∫_0^120 v(t) dt.
b) The integral 120 ∫ |v(t)| dt represents the distance that the particle travels in 120 seconds. This is because |v(t)| represents the magnitude of the velocity, or speed, of the particle at time t, regardless of its direction. Thus, the integral of |v(t)| over the time interval [0, 120] gives the total distance traveled by the particle during that time.
c) The integral 120 ∫ a(t) dt represents the change in velocity of the particle over the time interval [0, 120]. This can be seen by the fundamental theorem of calculus, which tells us that if f(x) is the derivative of g(x), then ∫ f(x) dx = g(x) + C, where C is a constant of integration. In this case, a(t) is the derivative of v(t), so the integral of a(t) over the time interval [0, 120] gives us the change in velocity of the particle during that time. Specifically, the value of the integral gives us the difference between the velocity of the particle at time t=120 and its velocity at time t=0.
To learn more about velocity visit:
https://brainly.com/question/18084516
#SPJ11
Given that 6RSB ~ 6ZQM, list the three pairs of congruent angles and state the three equal ratios of
corresponding sides.
Answers
Answer:
3ZSM 1
Step-by-step explanation:
THE FASTEST LEARNING TO HAVE ANSWERS
what is the multiplicative inverse of 5 2/3
Answers
Answer:
b=2 a=5
Step-by-step explanation:
What is the area of an equilateral triangle with sides 10 cm and altitude 5 cm
Answers
Answer:
25 cm^2
Step-by-step explanation:
The formula for the area of a triangle is \(1/2*base*height\).
We're given the base and height (altitude) in this question. The base is 10 cm and the height is 5 cm. All we have to do is plug them in to the formula now.
\(1/2*10*5\)
\(1/2*50\)
\(25\)
Explanation:
I’m smart :) jk
The mean mass of five men is 76 kg. The masses of four of the men are 72 kg, 74 kg, 75 kg and 81 kg. What is the mass of the fifth man
Answers
Answer:
78kg
Step-by-step explanation:
76×5= 380kg
380-72-74-75-81= 78kg
x=(76.5)-302
x=380-302=78
Please help! I need explanation on why the answer is what it is.

Answers
The graph that matches the given linear inequality is (B) .
In the question ,
it is given that
the linear inequality is y \(>\) -x + 4
on rewriting the inequality
we get
x + y \(>\) 4
to plot the inequality , we need points to plot .
So ,when x = 0 , we have y = 4
and when y = 0 , we have x = 4
so the two points are (0,4) and (4,0) .
For shading the inequality , we put x = 0 and y = 0 ,
and get 0+0 > 4
0>4 , the result is False , So , the shaded region will be away from the origin which is shown in option (b) .
Therefore , The graph that matches the given linear inequality is (B) .
Learn more about Inequalities here
https://brainly.com/question/26591602
#SPJ1
The length of a rectangle is 4yd longer than its width. If the perimeter of the rectangle is 40yd , find its area.
Answers
The area of rectangle is found to be 117 sq. yd.
Define the term perimeter of the rectangle?If you simply know the width and height, you can easily search all four sides, since two of them are equal to each of the height as well as the width. Add the results after dividing the height and breadth by two.Let the length of rectangle be L:
The, the width is W + 4 = L
Perimeter = 2(length + width)
P = 2(L + B)
P = 2(W + 4 + W)
P = 2(2W + 4)
40 = 4W + 4
4W =36
W = 9
The, L = 9 + 4 = 13 yd.
Area = length * width
Area = 9*13
Area = 117
Thus, the area of rectangle is found to be 117 sq. yd.
To know more about the perimeter of the rectangle, here
https://brainly.com/question/10452031
#SPJ4
Answer:
Step-by-step explanation:
What is perimeter of a Rectangle:The perimeter of a rectangle is the total circumference of the rectangle.
Perimeter=2(Length + breadth)
Perimeter=40yd
Length=x+4 and breadth=x
40=2(x+x+4);
40=4x+8;
4x=32 and x=8yd
So, length=12yd and breadth=8yd.
Area = length*breadth
So Area = 12*8= 96ydsq
To know more about perimeter of rectangle: https://brainly.com/question/30243597
#SPJ4
i need help with it like really teacher
Answers
Answer:
i think the answer is B
Step-by-step explanation:
sorry if this was wrong hoped i helped tho
please help me pls pls pls pls

Answers
Answer:
1. B: 47°
2. D: 41°
3. D: 22°
4. D: 80°
5. A: 32°
Step-by-step explanation:
Hope this helps!
assume you purchased some corporate stock 4 years ago for $7,500. You received quarterly dividends of 875 ; your dividends total $1,200 (16 dividend checks ×$75=$1,200). You sold the stock today for $8,050. 6. The PV is $8,050 because that is the amount you received today (in the present). (T or F ) 7. $1,200 represents which variable (PV, PMT, or FV)? 8. What is the FV amount? Unit 12.2 Financial calculators 9. When is it not necessary to clear the TVM registers? 10. By setting our "periods per year" register at 1 we must enter the periodic rate in the i-register. (T or F)
Answers
6. False. The present value (PV) is the initial investment or the amount invested in the stock, which is $7,500, not the amount received today ($8,050).
7. $1,200 represents the variable PMT (Payment). It represents the total dividends received over the four-year period.
8. The future value (FV) amount is $8,050, which is the amount received from selling the stock today.
9. It is not necessary to clear the TVM (Time Value of Money) registers when the calculations are completed, and you don't need to perform any further calculations.
10. True. When the "periods per year" register is set to 1, the periodic rate (interest rate) should be entered directly into the i-register as a decimal value, such as 0.05 for 5%.
Therefore, the PV is not $8,050 but $7,500, representing the initial investment. The variable $1,200 represents the PMT (payment) or the total dividends received. The FV amount is $8,050, the selling price of the stock. Clearing the TVM registers is not necessary after completing calculations, and when "periods per year" is set to 1, the periodic rate is entered directly into the i-register.
Learn more about initial investment visit:
https://brainly.com/question/29726908
#SPJ11