f(x) = 4x² + 5x – 3
g(x) = 4x³ - 3x² +5
Find (f - g)(x).
I need asap! Thank you!
Answers
Step-by-step explanation:
in this two image I think that you got is and the second image that I have written with blue colour that is incomplete so complete it and compare the answer


Related Questions
PLEASE HELP!!
Find the slope of the line described by 5x + 6y = -30
Answers
TO FIND THE SLOPE OF THIS LINE LET US FIRST ARRANGE IT TO THE GENERAL EQUATION OF A STRAIGHT LINE Y=MX+C
\(6y = - 30 - 5x \\ \frac{6y}{6} = \frac{ - 30}{6} - \frac{5x}{6} \\ y = - 5 - \frac{5x}{6} \)
WE KNOW THAT THE SLOPE OF A LINE IN THE GENERAL EQUATION OF A STRAIGHT LINE Y=MX+C IS THE COEFFICIENT OF X.
IN THIS CASE THE SLOPE OF THE LINE IS
\( - \frac{5}{6} \)
GOODLUCK
Answer:
m= -5/6
Step-by-step explanation:
Use the slope-intercept form
y=mx+b to find the slope
Delia graphed AABC
AA'B'C'.
on the coordinate grid as shown. She applied a series of transformations which produced a simillar triangle that she labeled. What sequence of transformation did Delia use to produce triangle A’ B’C
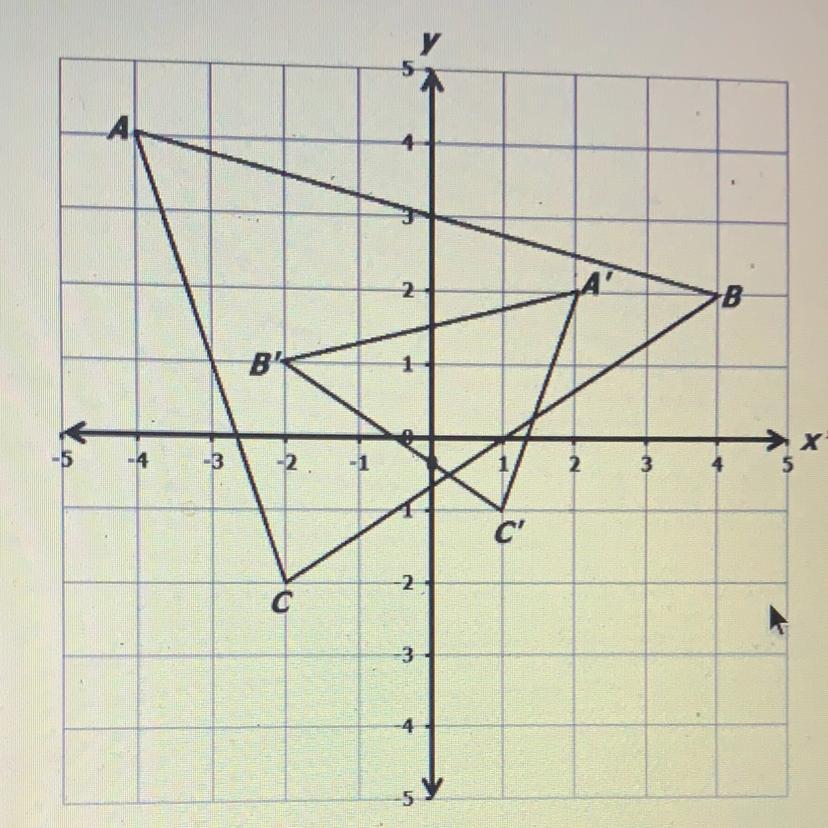
Answers
Answer:
You should watch SHREK
Step-by-step explanation:
Fritz can build a bookcase in 8 hours and Holly can build the same bookcase in 10 hours. After working together for 3 hours, Fritz leaves how long will it take holly to finish the bookcase by herself?
Answers
Holy will take 13/5 or 2.6 hours to finish the bookcase.
What is relation between time and work?The relation between time and work is
Work Done = Time Taken × Rate of Work ·
or, Rate of Work = 1 / Time Taken ·
or, Time Taken = 1 / Rate of Work ·
Now it is given that,
Time taken by Fritz to build a bookcase = 8 hours
So, Bookcase build by Fritz in 1 hour = 1/8
Similarly,
Time taken by Holly to build a bookcase = 10 hours
So, Bookcase build by Holly in 1 hour = 1/10
So, bookcase build in 3 hours
Fritz = 3/8
Holly = 3/10
Total bookcase build in 3 hours = 3/8 + 3/10 = 27/40
So. remaining work = 1 - 27/40 = 13/40
Thus, Time taken by Fritz to complete the bookcase = 8 * (13/40) hours
= 13/5 or 2.6 hours
Thus, Holy will take 13/5 or 2.6 hours to finish the bookcase.
To learn more about work and time:
brainly.com/question/24253661
#SPJ4
Which equation represents the line shown on the graph?
A- y=-2x
B- y=x+2
C- y= -x+2
D- y=2x

Answers
Answer:
B- y=-x+2
Step-by-step explanation:
I did this before
pls help me fast its not a test and dont give wrong awnser

Answers
100% = 4400
A meter is 100 centimeters, so a centimeter is one hundredth of a meter (0.01 meter). A meter was divided into two parts. One part was 0.37 meter long. How long was the other part?
Answers
Answer:
0.63 meters
Step-by-step explanation:
Given the following :
1 meter = 100 centimeters
1 centimeter will be (1/100)meter
1 meter is divided into two :
Assume x and y
One part = 0.37 meters, = x
Then y will be :
x + y = 1 meter
x = 0.37
0.37 + y = 1
y = 1 - 0.37
y = 0.63 meters
Hence, the other part will be 0.63 meters
Which of the following pairs of triangles can be proven congruent by SSS?

Answers
Answer:
D
Step-by-step explanation:
Help! my teacher gave me this exit ticket but I don't quite understand.

Answers
Answer:
4
-4
5
8
Step-by-step explanation:
you just divied like normal but if you have two negitives you will end out with the positve of the number
The speed of light is 3 x 10^8 meters/second. If the sun is 1.5 X 10^11 meters from earth, how many seconds does it take the sunlight to reach the Earth? (Time = Distance/Speed).
Answers
Answer:
Time = 500 seconds or 8.333 minutes
Step-by-step explanation:
Time = Distance/Speed
Speed of light = 3 x 10^8 meters/second
Distance=1.5 X 10^11 meters
Time = 1.5 X 10^11 meters/3 x 10^8 meters/second
We solve using the scientific notation. When 8 is taken to the top it is subtracted from 11 ( the base 10 is the same -- laws of exponents)
Dividing 1.5 by 3 gives 0.5 .
Time = 1.5 X 10^(11- 8) meters/3 meters/second
Time = 0.5 X 10^3 seconds
Time = 500 seconds
Dividng seconds with 60 will give minutes
Time= 500/60 = 8.333 minutes
Ms. Wells is going to order 4 large cheese pizzas for a class pizza party at the end of the school year. She expects she'll spend at least $40 on the pizzas. Let x represent how much ms. Wells expects each pizza to cost. Which inequality describes the problem?.
Answers
The correct inequality that describes the problem is 4x ≥ 40. Thus, the correct answer is A.
The answer is A because Ms. Wells is ordering 4 large cheese pizzas, and she expects to spend at least $40 on the pizzas. The inequality 4x ≥ 40 represents the total cost of the pizzas, which is 4 times the cost of each pizza (4x) and should be greater than or equal to $40. This inequality tells us that the total cost of the pizzas is at least $40, which is what Ms. Wells expects.
Option B, 4x > 40x, is incorrect because it doesn't make sense mathematically. The right side of the inequality is 40x, which is not related to the problem, and it also doesn't make sense that each pizza will cost 40 dollars.
Option C, 4x ≤ 40, is incorrect because it represents the total cost of the pizzas as less than or equal to $40, which doesn't match with Ms. Wells' expectation that she expects to spend at least $40 on the pizzas.
This question should be provided with answer choices, which are:
A. 4x ≥ 40B. 4x > 40xC. 4x ≤ 40The correct answer is A.
Learn more about inequality here: brainly.com/question/25944814
#SPJ4
Why did Keynes think deficit spending was necessary during periods of recession (such as the Great Depression)?
Answers
Answer:
Keynes argued that inadequate overall demand could lead to prolonged periods of high unemployment. But during a recession, strong forces often dampen demand as spending goes down
Step-by-step explanation:
Substance A decomposes at a rate proportional to the amount of A present. It is found that 14 ib of A will reduce to 7 lb in 3.9 hr. After how long will there be only 1 lb left? There will be 1 blot atter hr (Do not round until the final answer. Then round to the nearest whicle number as needed.)
Answers
Answer: The amount of Substance A remaining after t hours is
N(t) = N₀ \(e^(-kt)\)
= 14 \(e^(-0.1773t)\)
We are to find at what time t will there be only 1 lb left
N(t) = 1,
which implies
14 \(e^(-0.1773t)\) = 1
\(e^(-0.1773t)\) = 1/14
t = -ln(1/14)/0.1773
t = 11.012 hours
Therefore, there will be 1 lb left after 11 hours.
Step-by-step explanation:
Given that Substance A decomposes at a rate proportional to the amount of A present and it is found that 14 lb of A will reduce to 7 lb in 3.9 hr.
The amount of Substance A present at any time t is given by:
N(t) = N₀ \(e^(-kt)\),
whereN₀ is the initial amount of Substance A present
k is the proportionality constant is the time passed and N(t) is the amount of Substance A present after time t.
Since 14 lb of A reduces to 7 lb in 3.9 hours,N(t=3.9) = 7lb, and N₀ = 14 lb.
Substituting these values in the above equation,
N(3.9) = 14\(e^(-k*3.9)\)
= 7
Dividing both sides by 14\(e^(-k*3.9)\), we have,
1/2 = \(e^(-k*3.9)\)
Taking natural logarithm on both sides,
-ln2 = -k*3.9
k = ln2/3.9
= 0.1773
To know more about amount visit:
https://brainly.com/question/32453941
#SPJ11
Which of the following is a factor of 9x^2-81?
x-27
3x-3
x-3
x-9
Answers
\(Hello\) \(There!\)
I'll be helping your question today!
Let's do this step-by-step explanation!
\(9x^2-81\)
Factor out common term 9: \(9(x^2-9)\)
\(=9(x^2-9)\)
Factor:\(x^2-9:(x+3)(x-3)\)
\(=9(x+3)(x-3)\)
Answer:
\(9(x+3)(x-3)\)
The real answer is:
\(3x-3\)
Hopefully, this helps you!!
#LearnWithBrainlyAlways~
\(SokkaBanned\)
The factorization of \(9x^2 - 81\) is given 9(x-3)(x+3). Therefore, (c) is the correct option.
Factorization is the method of simplification of algebraic expressions which contains variables and constants into form that can not be divided into further factors.
To factorize, we first check if any variable or constant can be taken common. Next we check for algebraic identities.
Given in the question,
\(= 9x^2 - 81\\\\= 9(x^2 - 9)\\\\=9(x^2-3^2)\\\\=9(x-3)(x+3)\)
identity used : \((a^2-b^2) = (a-b)(a+b)\)
Learn more about factorization here
https://brainly.com/question/34290719
#SPJ2
Locate all the critical points of the function f(x,y)=8x−x^2−4xy^2.
Answers
To locate the critical points of the function f(x, y) = 8x − \(x^{2}\)− 4x\(y^{2}\), we need to find the values of x and y where the partial derivatives of the function with respect to x and y are equal to zero.
Taking the partial derivative of f(x, y) with respect to x, we get:
∂f/∂x = 8 - 2x - 4\(y^{2}\)
Setting this partial derivative equal to zero and solving for x, we have:
8 - 2x - 4\(y^{2}\) = 0
-2x = 4\(y^{2}\) - 8
x = 2 - 2\(y^{2}\)
Now, taking the partial derivative of f(x, y) with respect to y, we get:
∂f/∂y = -8xy
Setting this partial derivative equal to zero and solving for y, we have:
-8xy = 0
xy = 0
From the equation xy = 0, we can see that either x or y must be equal to zero.
Therefore, the critical points of the function f(x, y) = 8x − \(x^{2}\) − 4\(xy^{2}\) are given by the pairs (x, y) where x = 2 - 2\(y^{2}\) and either x = 0 or y = 0.
Learn more about partial derivative here:
https://brainly.com/question/14782333
#SPJ11
Write an expression for the nth term of the sequence. (your formula should work for n = 1, 2, .) 1 2 , 1 3 , 1 7 , 1 25 , 1 121 ,
Answers
The nth term of the sequence can be expressed as: \(1 / (n^2)\)
The given sequence is: 1, 2, 1/3, 1/7, 1/25, 1/121, ...
To find an expression for the nth term of this sequence, we can observe that each term is the reciprocal of a specific pattern of numbers: 1, 2, 3, 4, 5, 6, ...
Notice that the numerator of each term follows a pattern of increasing consecutive positive integers: 1, 2, 3, 4, 5, 6, ...
The denominator of each term follows a pattern of perfect squares: \(1^2, 2^2, 3^2, 4^2, 5^2, 6^2, ...\)
Therefore, the nth term of the sequence can be expressed as:
\(1 / (n^2)\)
So, the expression for the nth term of the sequence is \(1 / (n^2)\). This formula will work for n = 1, 2, 3, and so on.
Learn about sequence at:
https://brainly.com/question/28036578
#SPJ4
While driving your rental car on your vacation in Europe, you find that you are getting 12.7 km/L of gasoline. What does this value correspond to in miles per gallon
Answers
12.7*2.352=29.87
Answer: 29.87 Miles per Gallon
PLS HELP IM STUCK PLS

Answers
Answer:
32
Step-by-step explanation:
16*(1.09^8) = 31.88
Answer: \(Future~amount~=~\Large\boxed{32}\)
Step-by-step explanation:
Given expression
Future amount = 16 (1 + 0.09)⁸
Simplify values in the parenthesis
Future amount = 16 (1.09)⁸
Simplify the exponents
Future amount = 16 (1.99256)
Simplify by multiplication
\(Future~amount~=~\Large\boxed{32}\)
Hope this helps!! :)
Please let me know if you have any questions
Find the solution to the system of equations below.
2y = 2x - 8
2x + y = 5
Answers
Answer:
The solution to the system of equations is:
(x, y) = (3, -1)The graph is attached below.
Step-by-step explanation:
Given the system of equations
\(2y = 2x - 8\)
\(2x + y = 5\)
Let us solve the system of equations using the elimination method
\(\begin{bmatrix}2y=2x-8\\ 2x+y=5\end{bmatrix}\)
Arrange equation variables for elimination
\(\begin{bmatrix}2y-2x=-8\\ y+2x=5\end{bmatrix}\)
Multiply y + 2x = 5 by 2: 2y + 4x = 10
\(\begin{bmatrix}2y-2x=-8\\ 2y+4x=10\end{bmatrix}\)
subtracting the equations
\(2y+4x=10\)
\(-\)
\(\underline{2y-2x=-8}\)
\(6x=18\)
solve 6x = 18 for x
\(6x=18\)
Divide both sides by 6
\(\frac{6x}{6}=\frac{18}{6}\)
simplify
\(x=3\)
For 2y - 2x = -8 plug in x = 3
\(2y-2\cdot \:3=-8\)
\(2y-6=-8\)
Add 6 to both sides
\(2y-6+6=-8+6\)
Simplify
\(2y=-2\)
Divide both sides by 2
\(\frac{2y}{2}=\frac{-2}{2}\)
Simplify
\(y=-1\)
Therefore, the solution to the system of equations is:
(x, y) = (3, -1)The graph is attached below.

Two cards are drawn without replacement from a standard deck of 5252 playing cards. What is the probability of choosing a black card for the second card drawn, if the first card, drawn without replacement, was a diamond
Answers
The probability of choosing a black card for the second card drawn, if the first card, drawn without replacement, was a diamond is 26/51.
We are given that two cards are drawn without replacement from a standard deck of 5252 playing cards. We need to find the probability of choosing a black card for the second card drawn, if the first card, drawn without replacement, was a diamond.
So, let us first find the probability of drawing a diamond card from a deck of 52 cards:4/52 = 1/13 (There are 4 diamond cards in a deck of 52 cards)
Now, if we draw a diamond card in the first draw, there will be 51 cards left in the deck of which 26 are black. Therefore, the probability of drawing a black card after drawing a diamond card is:26/51
Therefore, the probability of choosing a black card for the second card drawn, if the first card, drawn without replacement, was a diamond is 26/51.
Summary:Two cards are drawn without replacement from a standard deck of 52 playing cards. The probability of choosing a black card for the second card drawn, if the first card, drawn without replacement, was a diamond is 26/51.
Learn more about probability click here:
https://brainly.com/question/13604758
#SPJ11
Given: 9x>-36.
Choose the solution set.
O [xlx>-4)
O'{x1x<-4}
O [xlx>4)
O [xlx<4)
Answers
[x | x > -4)
This can be read as "the set of all x such that x is greater than -4."
The volume of a cylinder is 112π cubic meters. Find the diameter of the cylinder when its height is 7 meters.
Answers
We first found the radius of the cylinder which is 4 meters, then we multiplied by a factor of 2 to get the diameter which is 8 meters
Mensuration of solids(Cylinder)Given Data
Volume of Cylinder = 112π cubic metersDiameter = 7 metersWe know that the expression for the volume of cylinder is given as
Volume of cylinder = πr^2h
Substituting our given data we have
112π = = πr^2h
cancel out the = π
112 = r^2*7
Divide both sides by 7
112/7 = r^2
16 = r^2
Square both sides we have
r = \(\sqrt{16}\)
r = 4 meters
Since r = 4
Diameter = 2*4
Diameter = 8 meters
Learn more about cylinders here:
https://brainly.com/question/9554871
2a + 2b = c for b
Solve for b
Answers
2a + 2b = c
Subtract 2a from both sides
2b = -2a + c
Divide both sides by 2
b = -a + (c/2)
2x + 5y = -5
x + 3y = 3
Find the solution to the system algebraically
Answers
Answer:
-2y=-5x=3
Step-by-step explanation:
Make sure every variable is on one side of the equation and you get the answer.
Slope of points (-2, -1) and (4, 3)
Answers
Answer:
The slope between the points (-2, -1) and (4, 3) is \(\frac{3}{2}\)
Step-by-step explanation:
First, we must know the equation for finding the slope.
\(Slope(m) = \frac{y2-y1}{x2-x1}\)
Next, we plug in the coordinate points.
\(m=\frac{4-(-2)}{3-(-1)}\)
\(m=\frac{6}{4}\)
Finally, we simplify this answer.
\(Slope = \frac{3}{2}\)
A particular cola brand advertises that each can contains 12 ozs. of soda. Ten cans are selected at random and the contents are measured. A 95% confidence interval constructed from the sample data is 11.97 ozs. to 12.05 ozs. Does the confidence interval provide convincing evidence that the true mean volume is different than 12 ozs.
Answers
According to the question, the confidence interval does not include the value of 12 ozs, indicating that the true mean volume could be different. This provides some evidence to suggest that the advertised claim of 12 ozs may not hold true.
To determine if the confidence interval provides convincing evidence that the true mean volume is different than 12 ozs, we need to examine whether the interval contains the value of 12 ozs or not.
In this case, the confidence interval is constructed from the sample data and is given as 11.97 ozs. to 12.05 ozs. Since the interval does not include the value of 12 ozs, it suggests that the true mean volume may be different from 12 ozs.
When constructing a confidence interval, we specify a confidence level, which in this case is 95%. This means that if we were to repeat the sampling process multiple times and construct confidence intervals using each sample, approximately 95% of those intervals would contain the true mean volume.
However, in this particular instance, the confidence interval does not include the value of 12 ozs, indicating that the true mean volume could be different. This provides some evidence to suggest that the advertised claim of 12 ozs may not hold true.
The \(95\%\) confidence interval is constructed as (11.97, 12.05).
To know more about Volume visit-
brainly.com/question/30347304
#SPJ11
The summer and winter solstices are the longest day and night of the year, respectively. The summer solstice happens between June 20 and June 21, while the winter solstice is between December 21 and December 23. At a latitude of 28° the summer solstice is 14.5 hours long and the winter solstice is 14 hours long. Write a sinusoidal equation modeling the hours of daylight in a year. Use t for the variable and measure t in weeks. For the purposes of this problem, idealize a year to be 52 weeks long, with the winter solstice a week before the new year. h(t) = __________
Answers
The correct answer is h(t) = 14.25 + 0.25 * sin((π/26) * t)
To model the hours of daylight in a year using a sinusoidal equation, we can consider the average length of daylight, the amplitude of the variation, and the period of the function.
Given:
Summer solstice (longest day) is 14.5 hours
Winter solstice (longest night) is 14 hours
Let's analyze the information:
Average daylight: The average daylight throughout the year would be the average of the summer and winter solstices. It can be calculated as:
Average daylight = (14.5 + 14) / 2 = 14.25 hours
Amplitude: The difference between the average daylight and the longest day or night is the amplitude. In this case, the amplitude is half the difference between the summer and winter solstices. It can be calculated as:
Amplitude = (14.5 - 14) / 2 = 0.25 hours
Period: We are modeling the function over a year, which we'll consider as 52 weeks. Since we want to measure time in weeks (t), the period of the function is 52 weeks.
Putting all the information together, we can write the sinusoidal equation:
h(t) = Average daylight + Amplitude * sin((2π / Period) * t)
Substituting the values we calculated:
h(t) = 14.25 + 0.25 * sin((2π / 52) * t)
Simplifying further, the sinusoidal equation modeling the hours of daylight in a year is:
h(t) = 14.25 + 0.25 * sin(π/26 * t)
Learn more about function here:
https://brainly.com/question/11624077
#SPJ11
Create a table to match the word problem below and solve,
Guorts
Jenny was making omelets for her
farnily for breakfost. For every omelet she used 3 eggs
4 ounces of cheese, How many eggs and ounces of cheese did she use if there ore 5 people in
her family?
Answers
Sure! Here's a table to represent the information given in the word problem: Item Amount per Omelet Eggs 3 Cheese 4 ounces To find out how many eggs and ounces of cheese Jenny used for her family.
we need to multiply the amounts per omelet by the number of omelets she made. Since there are 5 people in her family, we assume she made one omelet per person. Therefore, she made a total of 5 omelets Using the table, we can calculate: Eggs: 3 eggs per omelet × 5 omelets = 15 eggs Cheese: 4 ounces of cheese per omelet × 5 omelets = 20 ounces of cheese So, Jenny used 15 eggs and 20 ounces of cheese for her family.
To find out how many eggs and ounces of cheese Jenny used for her family, we need to multiply the amounts per omelet by the total number of omelets she made. Since there are 5 people in her family, she needs to make 5 omelets Using the table, we can calculate Eggs: 3 eggs per omelet × 5 omelets = 15 eggs Cheese: 4 ounces of cheese per omelet × 5 omelets = 20 ounces of cheese.
To know more about amounts per omelet:-https://brainly.com/question/1372112
#SPJ11
Need help in rush...someone pls help me! And pls show work

Answers
Answer:
7.2 or 7.20 my work is explained below!
first divide $3.00 by 5. our answer would be .6 (check: .6x5=3)
so now we know .6 is the cost of 1 ticket. so next, we would multiply .6 by 12 to get our answer. our answer would be 7.2 or 7.20.
I hope this helped, have a good day / night! :)
Answer:
\(\frac{5}{3}=1.66666666667 \\1.66666666667 * 6 = 10\\10 * 2 = 20\)
Step-by-step explanation:
15) Write the word sentence as an equation: A number c is 7 greater than twice a number b. a) bb 7=C b) c = 2b = 7 c) 7 > 2b d) c=7 +2b
Answers
Since there are 2 numbers c and b
Since c is 7 greater than twice b
Twice b means 2 x b = 2b
7 greater than means c is greater by 7 than 2b
Then the equation should be
c = 7 + 2b OR c = 2b + c
The quadrilateral is a trapezoid. What is the value of x?
A. 4
B. 5
C. 48
D. 25
Answers
If the quadrilateral is a trapezoid , then the value of x is = (b) 5 .
We know that the Midsegment of a trapezoid is parallel to each of the base and it's length is one half the sum of the lengths of the bases.
From the figure , we can observe that ⇒ side lengths are 21 units, 27 units , and the sides are parallel to each other.
From the given diagram of the trapezoid , the below expression is true:
that means : ⇒ 5x-1 = (21 + 27)/2 ;
⇒ 2(5x - 1) = 21 + 27 ;
⇒ 10x = 48 + 2 ;
⇒ 10x = 50
On Divide both sides by 10 ;
we have ;
⇒ x = 50/10 ;
⇒ x = 5 .
Therefore , for the quadrilateral the value of x is = 5 .
Learn more about Trapezoid here
https://brainly.com/question/8643562
#SPJ4
The given question is incomplete , the complete question is
The quadrilateral in the below figure is a trapezoid. What is the value of x ?
(a) 4
(b) 5
(c) 48
(d) 25
